В этой статье мы начнем разбирать конденсаторы “по косточкам”. Мы узнаем, как зависит напряжение на конденсаторе от расстояния между пластин, в чем отличие поведения конденсатора в случаях, когда он подключен к источнику и когда нет. В последующих статьях – продолжение. Задача 1. Найти емкость сферического конденсатора, состоящего из двух концентрических сфер радиусами Как известно, Запишем потенциалы сфер: Разность потенциалов: Тогда емкость конденсатора равна (диэлектрическая проницаемость масла равна А радиус шара был бы равен Ответ: Диэлектрическая проницаемость парафина По формуле Ответ: 556 мкФ Задача 3. Площадь каждой пластины плоского конденсатора Диэлектрическая проницаемость воздуха Из формулы «вытащим» Ответ: 1 см Задача 4. Расстояние между обкладками плоского конденсатора увеличивают. Как изменится: а) электроемкость конденсатора; б) напряженность электрического поля; в) напряжение? Рассмотреть два случая: 1) конденсатор заряжен и отключен от источника тока; 2) конденсатор подключен к источнику тока. Здесь необходимо запомнить: если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Действительно, куда ему деваться? А если начать что-либо менять, то будут меняться емкость и напряжение. Если же конденсатор подключен к источнику, то напряжение на нем постоянно, и при любых вмешательствах (раздвинули пластины, вложили диэлектрик) будет меняться емкость и заряд. Тогда в первом случае (заряд постоянен!): так как Во втором случае (напряжение постоянно): напряженность поля уменьшится; емкость уменьшится. Задача 5. Плоский конденсатор состоит из двух пластин, площадью Диэлектрическая проницаемость слюды Ответ: 1,59 мкКл Задача 6. Плоский воздушный конденсатор, расстояние между пластинами которого Если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Тогда Ответ: Задача 7. С какой силой взаимодействуют пластины плоского воздушного конденсатора площадью Сила взаимодействия пластин может быть вычислена как произведение заряда пластины на напряженность поля пластины: Ответ: easy-physic.ru Задание 2.Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.С=ε*ε0*S/d , где ε - диэлектрическая проницаемость диэлектрика, ε0 - электрическая постоянная 8.85·10−12 Ф/м, S - площадь пластин, d - расстояние между пластинами. Задание 3. Переведем все величины из дано в систему СИ:S=100 см² = 0,01 м².d=1 мм = 0,001 м.Емкость плоского коденсатора:С=ε*ε0*S/dПодставим числа и определим емкость:С=ε*ε0*S/d=10000*(8,85*10^−12)*0,01/0,001=0,88*10^-6 Ф.Ответ: емкость конденсатора 0,88*10^-6 Ф ил 0,88 мкФ. задание 4.При последовательном соединении конденсаторов напряжения конденсаторов складывается, а заряд не меняется, емкость равна:1/С=1/С1+1/С2+1/С3+..+1/СnЕсли конденсаторы одинаковые:С=С1/n , где n - число конденсаторов. Задание 5.У нас емкость конденсаторов одинакова, воспользуемся формулой:С=С1/n=200/5=40 мкФ.Ответ: 40 мкФ. Задание 6.При параллельном соединении конденсаторов электроемкость конденсаторов складывается:С=С1+С2+С3+..+СnЕсли конденсаторы одинаковые:С=С1*n , где n - число конденсаторов. Задание 7.У нас емкость конденсаторов одинакова, воспользуемся формулой:С=С1*n=200*5=1000 мкФ.Ответ: 1000 мкФ. Задание 8.Энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную.W=C*U²/2 Задание 9.Энергия конденсатора:W=C*U²/2=(0,4*10^-9)*220²/2=9,68*10^-6 Дж.Ответ: энергия конденсатора 9,68*10^-6 Дж. Задание 10.Энергия конденсатора:W=q²/2C=*(8*10^-9)²/2*(0,4*10^-9)=80*10^-9 Дж.Ответ: энергия конденсатора 80*10^-9 Дж. vashurok.ru где U – разность потенциалов между пластинами конденсатора, d – расстояние между ними. Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь – система двух равных по модулю разноименных зарядов (+Q, - Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда q на плечо l, называется дипольным электрическим моментом Величина дипольного момента в первом приближении прямо пропорциональна приложенному полю E. Число силовых линий, пронизывающих элементарную площадку dS, нормаль n которой составляет угол α с вектором Е, определяет поток вектора электрической напряженности, т.е. где En – проекция вектора напряженности Е на нормаль n к площадке dS (рис. 4.3). Для произвольной замкнутой поверхности S, поток вектора напряженности Поток вектора напряженности зависит только от алгебраической суммы зарядов, охватываемых этой поверхностью, т.е. Выражение (4.12) составляет суть теоремы Гаусса: поток вектора Скачкообразное изменение вектора напряженности электрического поля и числа линий напряженности на границе диэлектриков создает ряд неудобств при расчете электрических полей. Поэтому вводят вспомогательное поле Вектор По теореме Гаусса поток вектора электрического смещения через любую замкнутую поверхность численно равен алгебраической сумме находящихся внутри этой поверхности зарядов Между потоком вектора электрического смещения и числом силовых линий напряженности имеется числовое равенство где ρ – объемная плотность зарядов, V – объем, в котором заключен заряд. Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя теорему Гаусса (4.15), определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность. Рассмотрим примеры расчета электростатических полей в вакууме с использованием теоремы Гаусса. Равномерно заряженная бесконечная плоскость создает однородное электростатическое, модуль напряженности которого равен где σ – поверхностная плотность зарядов, ε – диэлектрическая проницаемость среды, ε0 – электрическая постоянная. Две равномерно, с одинаковой поверхностной плотностью, и разноименно заряженные бесконечные параллельные плоскости (например, плоский конденсатор) создают однородное электростатическое поле в пространстве между плоскостями с напряженностью, модуль которого равен Если плоскость представляет собой диск радиусом R, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из центра диска на расстоянии а от нее Напряженность поля, образованного заряженной бесконечно длинной нитью (или цилиндром) где τ – линейная плотность заряда на нити, a – расстояние от нити до заряда. Если нить имеет конечную длину, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из середины нити на расстоянии а от нее, где Θ – угол между направлением нормали к нити и радиус – вектором, проведенным из рассматриваемой точки к концу нити. Напряженность и потенциал поля, создаваемого проводящей заряженной сферойрадиусом R на расстоянии r от центра сферы где Q – заряд сферы. infopedia.su Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую. При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q. Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U. Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U. Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q. Полученный результат мы можем записать в виде следующей математической формулы: W = UQ/2 (1) Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде: W = CU2/2 (2) Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами. Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах. ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! www.sxemotehnika.ru – это устройство, обладающее относительно большой емкостью при малых размерах. Он представляет собой два проводника находящихся вблизи и изолированных друг от друга диэлектриком. Проводники в конденсаторе выполняются либо в виде металлических пластин, либо в виде обкладок из металлической фольги. Диэлектрики применяются различные: воздух, керамика, слюда, пластмассы, бумага и другие. Имеется большое количество типов конденсаторов, которые различаются между собой по конструкции и применяемым диэлектрикам. Емкость конденсатора определяется теми же факторами, которые влияют на емкость одиночных проводников: площадь поверхности пластин, расстояние между пластинами, диэлектрическая проницаемость диэлектрика между пластинами.Простейшим является плоский конденсатор, Он представляет собой две плоскопараллельные металлические пластины, разделенные диэлектриком. Емкость плоского конденсатора определяется по формуле где С – емкость конденсатора, ф; εa – абсолютная диэлектрическая проницаемость диэлектрика конденсатора; S – площадь одной стороны пластины конденсатора, м2 ; d – расстояние между пластинами конденсатора, м. Из формулы следует, что емкость конденсатора прямо пропорциональна поверхности пластин, обратно пропорциональна расстоянию между пластинами и зависит от диэлектрика конденсатора. Зависимость емкости конденсатора от площади пластин объясняется тем, что при большей поверхности пластин на них помещается больший по величине электрический заряд при данном напряжении. Зависимость емкости конденсатора от диэлектрической проницаемости диэлектрика объясняется явлением поляризации диэлектрика: чем больше диэлектрическая проницаемость, тем больше связанных зарядов в диэлектрике и на обкладках конденсатора и, следовательно, меньше электрический потенциал пластин конденсатора и напряжение между ними. Зависимость емкости конденсатора от расстояния между пластинами объясняется взаимным влиянием между зарядами в результате электростатической индукции: чем меньше расстояние между пластинами, тем сильнее их взаимное влияние, больше связанных зарядов, меньше электрический потенциал пластин и напряжение между ними, больше емкость конденсатора. Основными характеристиками конденсатора являются емкость и рабочее напряжение, Емкость конденсатора характеризует его способность накоплять электрические заряды. На основании формулы Номинальным рабочим напряжением конденсатора называется наибольшее напряжение между его обкладками, при котором он может надежно и длительно работать, сохраняя свои основные рабочие характеристики при всех установленных для него рабочих температурах. Если конденсатор работает под напряжением выше номинального, надежность его работы и срок службы сокращаются, Рабочее напряжение конденсатора должно быть значительно ниже его пробивного напряжения, т. е. напряжения при котором происходит разрушение его диэлектрика от действия электрического поля. Электрический пробой конденсатора заключается в пробое его диэлектрика. При этом диэлектрик разрушается, обкладки частично расплавляются и электрически соединяются между собой. Важным параметром конденсатора является сопротивление изоляции. Это одна из характеристик диэлектрика конденсатора. Так как нет абсолютных диэлектриков, то нет и конденсатора, сопротивление которого равно бесконечности. При включении конденсатора в электрическую цепь постоянного тока сила тока через конденсатор (ток утечки) зависит от сопротивления изоляции. Современные конденсаторы имеют сопротивление изоляции в несколько тысяч мегом. nauchebe.net ЭЛЕКТРОДИНАМИКА. РЕШЕНИЕ ЗАДАЧ. ЗАДАЧА 6. Как изменятся напряженность электрического поля, напряжение и энергия заряженного плоского воздушного конденсатора при увеличении расстояния между пластинами в два раза? Решение: Возможны два случая. 1. Если конденсатор заряжен до напряжения U и отключен от источника тока, то при раздвижении пластин неизменной величиной является электрический заряд q на его пластинах. При увеличении расстояния d между пластинами электроемкость конденсатора уменьшается в два раза. Поэтому напряжение увеличивается в два раза. Напряженность Е поля между пластинами при одинаковом увеличении напряжения U и расстояния d остается постоянной. Энергия конденсатора равна Так как заряд q постоянен, а электроемкость С уменьшается в два раза, то энергия увеличивается в два раза. Увеличение энергии в два раза происходит за счет работы внешних сил, совершаемой при раздвижении пластин конденсатора. 2. Если конденсатор подключен к источнику тока, напряжение между его пластинами при их раздвигании остается постоянным. Напряженность поля при постоянном напряжении U и увеличении в два раза расстояния d уменьшается в два раза. Энергия конденсатора равна При постоянном напряжении U и уменьшении в два раза электроемкости C энергия уменьшается в два раза. Уменьшение энергии заряженного конденсатора происходит потому, что с уменьшением электроемкости при раздвигании пластин электрический заряд на его пластинах убывает в два раза, т.е. конденсатор разряжается. www.1variant.ruПлоский конденсатор: емкость, напряжение, напряженность и прочее. Напряжение между пластинами конденсатора
емкость, напряжение, напряженность и прочее
м и 
м. Пространство между сферами заполнено маслом. Какого радиуса должен быть изолированный шар, чтобы он имел емкость, равную емкости такого конденсатора?
):
пФ, 
м.Задача 2. Найти емкость плоского конденсатора, состоящего из двух круглых пластин диаметром 
см, разделенных парафиновой прослойкой толщиной 
мм.
.
см
. На каком расстоянии друг от друга надо расположить в воздухе пластины, чтобы емкость конденсатора была 
пФ?
.
:
зависимость емкости от обратная, то емкость будет падать при увеличении расстояния между пластинами. Напряженность 
– никак не зависит от расстояния между обкладками, она не изменится; напряжение 
– увеличится, оно от величины зависит прямо.
см каждая, расположенных на расстоянии 
мм друг от друга, между которыми находится слой слюды. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение 
кВ?
.
мм, заряжен до напряжения 
В и отключен от источника. Каким будет напряжение 
, если пластины раздвинуть до расстояния 
мм?
В
м, если напряжение на пластинах 
В и расстояние между ними 
м?
– делим пополам, потому что напряженность поля одной пластины вдвое меньше напряженности поля конденсатора – там пластин две штуки.
мН.1 Вычислите напряжение между пластинами конденсатора, если электроемкость конденсатора 0,5 мкФ. 200В, а заряд а одной
Задание 1.Переведем все величины из дано в систему СИ:q=2 нКл = 2*10^-9 Кл.C=0,5 мкФ = 0,5*10^-6 Ф.Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:С=q/U, выразим из этого выражения напряжение:U=q/C=2*10^-9/0,5*10^-6=0,004 В.Ответ: 0,004 В или 4 мВ.Напряженность поля между пластинами конденсатора
,
(4.8)
,
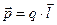(4.9)
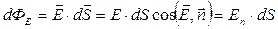, (4.10) 
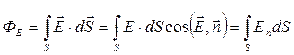(4.11)
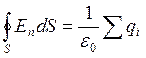(4.12)
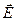сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на электрическую постоянную 
.
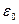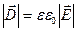. (4.13)
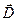, равный произведению вектора напряженности 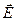электрического поля на абсолютную диэлектрическую проницаемость среды в данной точке, носит название вектора электрического смещения.
. (4.14)
, (4.15)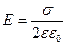 
,
(4.16)
.
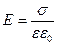(4.17)
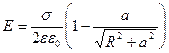
(4.18)
,
(4.19)
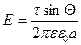
(4.20)
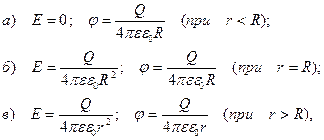
(4.21)
Энергия поля конденсатора - Основы электроники
Похожие материалы:
Добавить комментарий
Электрический конденсатор | Техника и Программы
Задача 6. Как изменятся напряженность электрического
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''
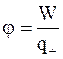
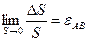
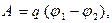
Поделиться с друзьями: