Работа получается положительной, так как сила и перемещение сонаправлены. C другой стороны, работа поля есть произведение заряда на разность потенциалов между точками 1 и 2: A = qU: (Напряжение также положительно, так как '1 > '2 ведь напряжённость направлена в сторону убывания потенциала.) Приравнивая правые части последних двух формул, получим: qU = qEd, откуда Эта простая формула позволяет находить напряжение между точками однородного поля E, находящимися на одной силовой линии; при этом напряжённость поля направлена от начальной точки к конечной. Выразим из формулы (3.21) напряжённость: E = U : (3.22) d Эта формула пригодится нам впоследствии, при нахождении напряжённости поля в конденсаторе. А сейчас обратим внимание на одно следствие данной формулы: единицей измерения напряжённости является В/м. Эта единица используется чаще, чем первоначальная Н/Кл. Что ж, немало вещей пришлось узнать, чтобы понять равенство Н/Кл = В/м :-) Как вы помните, введение силовой характеристики поля (напряжённости) дало возможность изображать поле графически в виде картины линий напряжённости, или силовых линий. Энергетическая характеристика поля (потенциал) также позволяет дать графическую картину поля в виде семейства эквипотенциальных поверхностей. Поверхность в пространстве называется эквипотенциальной, если во всех точках этой поверхности потенциал электрического поля принимает одно и то же значение. Коротко говоря, эквипотенциальные поверхности это поверхности равного потенциала. Например, из формулы ' = Ex мы видим, что эквипотенциальными поверхностями однородного поля являются всевозможные плоскости x = const. Они перпендикулярны линиям напряжённости. Так, на рис. 3.21 изображены пять плоскостей эквипотенциальных поверхностей, отвечающих значениям потенциала '1, '2, '3, '4 и '5. E '1'2'3'4'5 Рис. 3.21. Эквипотенциальные поверхности однородного поля Теперь рассмотрим нашу вторую стандартную ситуацию: поле точечного заряда q > 0. Потенциал этого поля, как мы уже видели, равен: ' = kqr : studfiles.net Важнейшим понятием, используемым в электрике, радиотехнике и в любой другой сфере, связанной с электричеством, выступает разность потенциалов между точками, или более привычное название – электрическое напряжение. С виду простое понятие включает в себя довольно много аспектов и тезисов. Энергопотенциалы в электрическом поле Первоначально охарактеризуем сам термин, что такое разность потенциалов. Такая разница в потенциалах между двумя точками, находящимися на некотором расстоянии (А и Б), есть значение, прямо пропорциональное проведенному действию среды по переносу источника электромагнитного фона со знаком «+» из одной точки в другую и обратно пропорциональная величине самого источника электромагнитного поля. Как найти разность потенциалов, отображено формулой: φ1-φ2=А1-2/q, где: Потенциальная разница имеет свою единицу измерения – вольт. Итальянский физиолог, военный инженер и физик А.Вольт занимался этой проблематикой и явил миру ряд понятий: разность потенциалов и электрическое напряжение, назвав единицу измерения своей фамилией. По системе СИ характеристика 1 Вольт прямо пропорциональна параметру 1 Джоуль и обратно пропорциональна 1 Кулону. Токопроводящие материалы при более детальном рассмотрении состоят из плотно прилегающих друг к другу ядер вещества, не способных самостоятельно передвигаться. Вокруг этих ядер находятся мелкие частички, вращающиеся с огромной скоростью и называемые электронами. Их скорость настолько велика, что они способны отрываться от своих ядер и присоединяться к другим и таким образом беспрепятственно передвигаться по материалу. Молекула или частичка будет считаться электрически нейтральной при условии, что численность электронов в молекуле соответствует уровню протонов в ядре. Если же забрать некоторое число свободно вращающихся отрицательно заряженных частиц, то молекула будет всячески стремиться восстановить их количество. Образуя вокруг себя положительную область со знаком «+», молекула будет стремиться притянуть к себе недостающее число отрицательно заряженных частиц. От численности недостающих электронов и будет зависеть ускорение и сила тока, с которой они будут притягиваться, и, соответственно, сила положительного фона. Проведя обратную операцию, добавив в молекулу лишних электронов, получим силу, старающуюся вытолкнуть лишний их объем и, соответственно, образующую электрическое поле, но уже со знаком «-» – отрицательная среда. Эта ускоряющая разность потенциалов заставляет все электроны двигаться в одном направлении. Силовые поля заряженных частиц Изучив это явление, французский физик Шарль Огюстен Кулон ввел физическую величину, которая определяла способность тел быть источником ЭМ фона и принимать участие в электромагнитном взаимодействии. Такая величина получила название электрический заряд, с величиной измерения Кулон. В итоге получены два источника ЭМ фона, один из которых стремится отдать излишек электронов, второй – притянуть электроны в достаточном количестве. Каждый такой заряд обладает своей «силой». Выражение, которое бы количественно характеризовало его сущность, представлено отношением: φ= W/q и пропорционально энергетике источника поля, размещенного в данной точке к этому заряду. Соответственно, этот показатель характеризует работу источника электромагнитного поля и является энергетической характеристикой области. В случае если имеется некоторое количество заряженных частиц, то, опираясь на принцип суперпозиции, суммарная энергия образовавшейся области равна сумме полей зарядов, сформированных каждым в отдельности: φсумм.=φ1+φ2+…+ φі. Поведение зарядов в электрическом поле Неотъемлемой частью расчетов выступает работа по перемещению заряда в электрической среде. Опираясь на то, что на положительный точечный источник электромагнитного поля q в электрическом поле с напряженностью Е действует сила: F=qE, на отрезке L совершается действие, равное: А=qElcos α. Одно из свойств электростатического поля повествует о возможности пренебречь траекторией движения заряда при совершении работы по перемещению между двумя точками, а учитывать только первоначальную и конечную точку и величину источника электромагнитного поля. Соответственно косинусом можно пренебречь: А=qEl=qE(l1-l2)=qEl1-qEl2, поскольку действие А является мерой измерения энергии, и: W=qEl. В результате работу находить достаточно легко: A=W1-W2=-(W2-W1). Исходя из формулы, определяющей величину энергопотенциала: φ= W/q и воспринимая работу А как разницу энергий, доказана формула потенциальной разницы: φ1-φ2=А1-2/q. Изложенный материал подробно раскрывает такие термины, как разность потенциалов и потенциал. Детально рассмотрены порядок возникновения заряженных частиц, электростатического поля и их поведение по отношению друг к другу. Дополнительно рассмотрено ряд законов, касающихся основ электродинамики. elquanta.ru Работа получается положительной, так как сила и перемещение сонаправлены. C другой стороны, работа поля есть произведение заряда на разность потенциалов между точками 1 и 2: A = qU: (Напряжение также положительно, так как '1 > '2 ведь напряжённость направлена в сторону убывания потенциала.) Приравнивая правые части последних двух формул, получим: qU = qEd, откуда Эта простая формула позволяет находить напряжение между точками однородного поля E, находящимися на одной силовой линии; при этом напряжённость поля направлена от начальной точки к конечной. Выразим из формулы (3.21) напряжённость: E = U : (3.22) d Эта формула пригодится нам впоследствии, при нахождении напряжённости поля в конденсаторе. А сейчас обратим внимание на одно следствие данной формулы: единицей измерения напряжённости является В/м. Эта единица используется чаще, чем первоначальная Н/Кл. Что ж, немало вещей пришлось узнать, чтобы понять равенство Н/Кл = В/м :-) Как вы помните, введение силовой характеристики поля (напряжённости) дало возможность изображать поле графически в виде картины линий напряжённости, или силовых линий. Энергетическая характеристика поля (потенциал) также позволяет дать графическую картину поля в виде семейства эквипотенциальных поверхностей. Поверхность в пространстве называется эквипотенциальной, если во всех точках этой поверхности потенциал электрического поля принимает одно и то же значение. Коротко говоря, эквипотенциальные поверхности это поверхности равного потенциала. Например, из формулы ' = Ex мы видим, что эквипотенциальными поверхностями однородного поля являются всевозможные плоскости x = const. Они перпендикулярны линиям напряжённости. Так, на рис. 3.21 изображены пять плоскостей эквипотенциальных поверхностей, отвечающих значениям потенциала '1, '2, '3, '4 и '5. E '1'2'3'4'5 Рис. 3.21. Эквипотенциальные поверхности однородного поля Теперь рассмотрим нашу вторую стандартную ситуацию: поле точечного заряда q > 0. Потенциал этого поля, как мы уже видели, равен: ' = kqr : studfiles.net Разностью потенциалов между точками 1 и 2 называется работа, совершаемая силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2. для потенциальных полей эта работа не зависит от формы пути, а определяется только положениями начальной и конечной точек потенциал определен с точностью до аддитивной постоянной. Работа сил электростатического поля при перемещении заряда q по произвольному пути из начальной точки 1 в конечную точку 2 определяется выражением Практической единицей потенциала является вольт. Вольт есть разность потенциалов между такими точками, когда при перемещении одного кулона электричества из одной точки в другую электрическое поле совершает работу в один джоуль. 1 и 2 — бесконечно близкие точки, расположенные на оси х, так что Х2 — х1 = dx. Работа при перемещении единицы заряда из точки 1 в точку 2 будет Ех dx. Та же работа равна . Приравнивая оба выражения, получим - градиент скаляра Градиент функцииесть вектор, направленный в сторону максимального возрастания этой функции, а его длина равна производной функциив том же направлении. Геометрический смысл градиента– эквипотенциальные поверхности ( поверхности равного потенциала) поверхность, на которой потенциал остается постоянным. Потенциал поля точечного заряда q в однородном диэлектрике. - электрическое смещение точечного заряда в однородном диэлектрикеD –вектор электрической индукции или электрического смещения В качестве постоянной интегрирования следует взять нуль, чтобы при потенциал обратился в ноль, тогда Потенциал поля системы точечных зарядов в однородном диэлектрике. Используя принцип суперпозии получаем: Потенциал непрерывно распределенных электрических зарядов. - элементы объема и заряженных поверхностей с центрами в точке - в случае если диэлектрик неоднороден, то интегрирование надо распространить и на поляризационные заряды. Включение таких зарядов автоматически учитывает влияние среды, и величину вводить не надо Электрическое поле в веществе. Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. При наличии внешнего поля происходит перераспределение заряженных частиц, и в веществе возникает собственное электрическое поле. Полное электрическое поле складывается в соответствии с принципом суперпозиции из внешнего поля и внутреннего поля , создаваемого заряженными частицами вещества. Вещество многообразно по своим электрическим свойствам. Наиболее широкие классы вещества составляют проводники и диэлектрики. Проводник - это тело или материал, в котором электрические заряды начинают перемещаться под действием сколь угодно малой силы. Поэтому эти заряды называют свободными. В металлах свободными зарядами являются электроны, в растворах и расплавах солей (кислот и щелочей) - ионы. Диэлектрик - это тело или материал, в котором под действием сколь угодно больших сил заряды смещаются лишь на малое, не превышающее размеров атома расстояние относительно своего положения равновесия. Такие заряды называются связанными. Свободные и связанные заряды. СВОБОДНЫЕ ЗАРЯДЫ 1) избыточные электрич. заряды, сообщённые проводящему или непроводящему телу и вызывающие нарушение его электронейтральности. 2) Электрич. заряды носителей тока. 3) положит. электрич. заряды атомных остатков в металлах. СВЯЗАННЫЕ ЗАРЯДЫ Электрич. заряды частиц, входящих в состав атомов и молекул диэлектрика, а также заряды ионов в кристаллич. диэлектриках с ионной решёткой. studfiles.net Так как потенциальная энергия системы электрических зарядов пропорциональна величинам зарядов, то, помещая в одну и ту же точку поля различные по величине заряды, будет изменяться потенциальная энергия. Однако отношение потенциальной энергии системы зарядов к величине помещаемого в данную точку поля электрического заряда остается постоянным, следовательно, оно может служить характеристикой электрического поля. Потенциальную энергию положительного единичного заряда, помещенного в данную точку поля, называют потенциалом электрического поля j. Потенциал электрического поля Если поле создано положительным точечным зарядом q, то где q – величина заряда, создающего электрическое поле; r – расстояние от центра заряда до рассматриваемой точки поля. Потенциал электрического поля системы точечных зарядов равен алгебраической сумме потенциалов полей, создаваемых отдельно взятым зарядом системы: где qi – величина i-го заряда; ri – расстояние от i-го заряда до рассматриваемой точки поля. Из выражения (1.31) W = qj. (1.34) Так как работа сил электрического поля равна убыли потенциальной энергии, т.е. A1,2 = - DW = W1 - W2 = q(j1 - j2), (1.35) то При q = q+ = 1 Таким образом, разность потенциалов между двумя точками поля, численно равна работе, которую совершают силы электрического поля по перемещению положительного единичного заряда из одной точки поля в другую. При перемещении положительного единичного электрического заряда из данной точки поля в бесконечность A1,¥ = W1 - W¥ = qj1, а Если q = q+ = 1, то Следовательно, потенциал электрического поля численно равен работе сил электрического поля по перемещению положительного единичного заряда из данной точки поля в бесконечность. Потенциал и разность потенциалов электрического поля являются его энергетическими характеристиками. В системе СИ потенциал и разность потенциалов измеряются в вольтах. Один вольт – это потенциал такой точки электрического поля, находясь в которой заряд в 1 Кл обладает потенциальной энергией, равной 1 Дж. 1.8.2. Связь напряженности электрического поля с его потенциалом Каждая точка электрического поля характеризуется напряженностью и потенциалом (силовой и энергетической характеристиками). Между ними должна существовать связь, которую можно установить исходя из следующих соображений. Элементарная работа, совершаемая силами электрического поля по перемещению электрического заряда на расстояние dl, dA = F∙dl∙cosa = Fl∙dl = qEl∙dl. Работа совершается за счет убыли (уменьшения) потенциальной энергии: dA = - dW = - q×dj. Следовательно, имеем qEl×dl = - q×dj. Отсюда где l – произвольно выбранное направление. В векторной форме E = - grad j. (1.41) Знак "минус" означает, что вектор напряженности электрического поля направлен в сторону убывания потенциала. Проинтегрировав формулу dj = - El×dl, получим Откуда где d = l×cosa - расстояние между точками 1 и 2 поля. В векторной форме выражение (1.41), можно представить так: Зная теорему Остроградского-Гаусса и связь между напряженностью и потенциалом электрического поля, можно по известной величине определить неизвестную. 3.4.6Разность потенциалов. Напряжение через разность потенциалов
Разность потенциалов
3.4.9Эквипотенциальные поверхности
Формула нахождения потенциальной разницы между точками в электромагнитном поле
Сущность понятия потенциальной разницы
Поведение заряженных частиц
Видео
Оцените статью: Разность потенциалов
3.4.9Эквипотенциальные поверхности
12 Разность потенциалов
13 Потенциал зарядов
14 Электрическое поле в веществе
Потенциал и разность потенциалов электрического поля
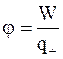 . (1.31)
. (1.31)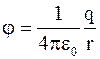 , (1.32)
, (1.32) , (1.33)
, (1.33) . (1.36)
. (1.36) . (1.37)
. (1.37)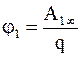 . (1.38)
. (1.38) . (1.39)
. (1.39) , (1.40)
, (1.40) характеризует быстроту изменения потенциала в данном направлении l и называется градиентом потенциала;
характеризует быстроту изменения потенциала в данном направлении l и называется градиентом потенциала;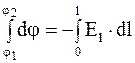 ;
; .
.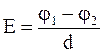 , (1.42)
, (1.42)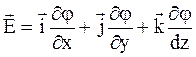 . (1.43)
. (1.43)Похожие статьи:
poznayka.org


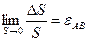








Поделиться с друзьями: