Cтраница 1 Полные напряжения получим согласно принципу сложения действия сил. [1] Полное напряжение р можно разложить на две составляющие ( рис. 1.13, а): 1) составляющую, нормальную к плоскости сечения. [2] Полные напряжения в листах рессоры определяются суммированием ( с учетом знаков) напряжений затяжки с напряжениями, возникающими при действии внешних сил. [3] Полные напряжения подсчитывают по формулам ( см. табл. 1 гл. [4] Полное напряжение р и его составляющие опт являются векторами. Рассматривая нормальное или касательное напряжение по какому-либо определенному сечению, мы тем самым точно фиксируем их направление. Поэтому эти напряжения не требуется обозначать как векторы. Нормальные напряжения возникают при сближении или отрыве частиц тела, а касательные напряжения - при скольжении или сдвиге частиц. [5] Полное напряжение на клеммах электролизера определяется также дополнительным омическим сопротивлением, возникающим при прохождении тока через электролит, а также через все токоподводящие приспособления и электроды. [6] Полное напряжение, действующее по этой грани, р, его составляющие по координатным осям рх, ру и рг. [7] Полное напряжение не считается удобной мерой оценки внутренних сил тела, так как материалы различным образом сопротивляются нормальным и касательным напряжениям. Нормальные напряжения стремятся сблизить или удалить отдельные частицы тела по направлению нормали к плоскости сечения. Касательные напряжения стремятся сдвинуть одни частицы тела относительно других по плоскости сечения. Поэтому касательные напряжения называют еще напряжениями сдвига. [8] Полное напряжение в момент подключения реактивности хэ распределяется между внутренней и внешней реактивностями цепи статора, как показано на рис. 10 - 8, и отношение ШШ дает искомую величину провала напряжения. [10] Полное напряжение в данной площади поперечного сечения обычно представляет собой геометрическую сумму двух напряжений-нормального и касательного. Нормальные напряжения стремятся вызвать отрыв частиц друг от друга ( при растяжении), а касательные напряжения - сдвиг частиц. [11] Полное напряжение по правилу параллелепипеда всегда можно разложить на три: одно нормальное и два касательных. [12] Полное напряжение р можно разложить на две составляющие ( рис. 1.13, а): 1) составляющую, нормальную к плоскости сечения. [13] Полное напряжение р на этой площадке, согласно условию однородности напряженного состояния для всех точек площадки, будет одним и тем же. [14] Полное напряжение, возникающее на секущей площадке, может быть разложено на три составляющие: одну по нормали к площадке и две в плоскости сечения. [15] Страницы: 1 2 3 4 www.ngpedia.ru Напряжение полное, нормальное, касательное. Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.). p Полное напряжение p Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – p Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением p Растяжение, сжатие. Продольные силы и их эпюры. Относительное продольное растяжение ( сжатие) твердого тела сопровождается его относительным сужением ( расширением) M / d, где d - поперечный размер образца. [1] Отношение продольного растяжения р к относительному продольному удлинению 8Х называется коэффициентом Е упругости при растяжении. [2] Коэффициент продольного растяжения - величина, обратная модулю Юнга. [3] Деформация продольного растяжения или сжатия сопровождается изменением поперечных размеров деформируемого стержня. [4] Характеристики продольного растяжения менее чувствительны к прочности связи, чем другие механические свойства. Бэйкер и Крэтчли [2] показали, что для оптимизации усталостных характеристик композита Al - Si02 необходима много более прочная вязь, чем для оптимизации продольных. Проблема оптимизации связи наиболее актуальна, для систем псевдопервого класса, и для полного понимания их поведения многое еще предстоит сделать. [5] При продольном растяжении ( рис. 5.1) процесс деформации прекращается, когда упругие силы становятся равными растягивающей силе F. [6] Растяжение и сжатие Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила.Продольные силы меняются по длине бруса. При расчётах после определения величин продольных сил по сечениям строится график - эпюра продольных сил.Условно назначают знак продольной силы Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией.Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией. Примеры построения эпюр Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплён в стене (закрепление «заделка») (рис. 30.)Делим брус на участки закрепления. Участком закрепления считают часть бруса между внешними силами.На представленном рисунке 3 участка нагружения.Расчёт начинаем со свободного конца бруса, чтобы не определять величины реакции в опорах.Участок 1 : Продольная сила положительна, участок 1 растянут. Участок 2: =F. Продольная сила положительна, участок 2 растянут.Участок .' Продольная сила отрицательна, участок з сжат. Полученное значение равно реакции в заделке.Под схемой бруса строим эпюру продольной силы (рис.31.).Эпюра продольной силы строится только под брусом. Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса.Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения чисел откладывают от оси, положительные - вверх, отрицательные вниз.В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.Правило контроля: в месте приложения внешней силы на эпюре должен быть скачек на величину приложенной силы.На эпюре проставляют значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.Эпюра по контуру обводится толстой линией и обводится поперёк оси.Принцип смягчения граничных условий гласит: в точках тела, удалённых от мест нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления. Продольное сжатие Разрушение при продольном сжатии может происходить в различных формах, которые показаны на рис.1: - микровыпучивание волокон при упругом или пластическом состоянии матрицы; - микровыпучивание волокон после нарушения адгезионной связи между ними и матрицей; - расслаивание; - выпучивание слоя; - сдвиговое разрушение слоя; - разделение слоев из-за поперечного растяжения в направлении толщины слоя (поперечное расслаивание от растяжения). Микровыпучивание волокон при упругих напряжениях в матрице возникает в слоях с весьма малой объемной долей волокон. Переход матрицы в пластическое состояние и отслаивание волокон от матрицы возникает, как правило, при объемной доле волокон y ? 0,4. Экспериментальные данные по продольному сжатию показывают, что слой не может выдерживать достаточно высокую сжимающую нагрузку, чтобы достигнуть полной прочности. При разрушении слоя от сжимающей нагрузки напряжение в волокнах значительно меньше их ожидаемой прочности на сжатие. а – микровыпучивание; б – отслаивание волокна от матрицы; в – выпучивание слоя; г – сдвиговые разрушения infopedia.su Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.). \textstyle \vec{p} = \lim_{\Delta A \to 0} {\Delta\vec{R}\over \Delta A} Полное напряжение [math]\vec p[/math], как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение [math]\tau_n[/math]. Здесь n – нормаль к выделенной площадке. Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_{nx}, \tau_{ny}[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения. $$\vec{p} = \left[\matrix{\sigma _n \\ \tau _{nx} \\ \tau _{nx}} \right]$$ Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением [math]\vec p [/math], а с его составляющими [math]σ_x,\tau _{xy}, \tau _{xz} [/math] . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ. Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений $$ T _\sigma = \left[\matrix{\sigma _x & \tau _{yx} & \tau _{zx} \\ \tau _{xy} & \sigma _y & \tau _{zy} \\ \tau _{xz} & \tau _{yz} & \sigma _z}\right]$$ Здесь первый столбец представляет компоненты напряжений на площадках,нормальных к оси x, второй и третий – к оси y и z соответственно. При повороте осей координат, совпадающих с нормалями к граням выделенногоэлемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю. Площадка, на которой касательные напряжения равны нулю, называется главной площадкой. Нормальное напряжение на главной площадке называется главным напряжением Нормаль к главной площадке называется главной осью напряжений . В каждой точке можно провести три взаимно-перпендикулярных главных площадки. При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС). Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению. Продольное усилие на площадке dA: dN = σzdAПоперечная сила вдоль оси х: dQ x = [math]\tau {zx}[/math] dAПоперечная сила вдоль оси y: dQ y = [math]\tau {zy}[/math] dAЭлементарные моменты вокруг осей x,y,z: $$\begin{array}{lcr} dM _x = σ _z dA \cdot y \\ dM _y = σ _z dA \cdot x \\ dM _z = dM _k = \tau _{zy} dA \cdot x - \tau _{zx} dA \cdot y \end{array}$$ Выполнив интегрирование по площади поперечного сечения получим: То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела. метки: напряжения sopromat.in.ua На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению. Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение представляет собой среднее напряжение на данной площадке. Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением. Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов. Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τx dA, τy dA. Суммируя проекции этих элементарных сил, а также их моменты относительно осей Ox, Oy, Oz, найдём; Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению. Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению. Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса. Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1). Рис. 3.1 Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений: Относительные деформации и напряжения связаны обобщенным законом Гука. Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2). Обозначение главных напряжений: Напряженное состояние называется объемным или трехосным, если Рис. 3.2 Относительное изменение объема: где К – модуль объемной упругости, Удельная потенциальная энергия упругой деформации: — полная — изменение объема — изменение формы Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3). Рис.3.3 Напряжения на наклонной площадке (рис. 3.4,а) Величина и направление главных напряжений (рис. 3.4,б) Чистый сдвиг σx = σy = 0 (рис. 3.4,в) Рис. 3.4 Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю. Проверка прочности при линейном напряженном состоянии проводится по условию прочности: В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению: Величина σэкв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием. Примеры расчета напряжений >Осевое растяжение-сжатие > isopromat.ru Напряжение – мера распределения внутренних сил по сечению. , где - внутренняя сила, выявленная на площадке . Полное напряжение . Нормальное напряжение – проекция вектора полного напряжения на нормаль обозначается через σ. , где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается. Касательное напряжение – составляющие напряжения в плоскости сечения. , где (для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига. Закон Гука для одноосного напряжённого состояния в точке и закон Гука для чистого сдвига. Модули упругости первого и второго рода, их физический смысл, математический смысл и графическая интерпретация. Коэффициент Пуассона. - закон Гука для одноосного напряжённого состояния в точке. Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см2. - закон Гука для сдвига. G – модуль сдвига (модуль упругости II рода). Размерность модуля G такая же, как и у модуля Е, т.е. кГ/см2. . μ – коэффициент Пуассона (коэффициент пропорциональности). . Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала). Центральное растяжение (сжатие) прямого бруса. Определение внутренних продольных сил методом сечений. Правило знаков для внутренних продольных сил. Привести примеры расчёта внутренних продольных сил. Брус испытывает состояние центрального растяжения (сжатия) в том случае, если в его поперечных сечениях возникают центральные продольные силы Nz (т.е. внутренняя сила, линия действия которой направлена по оси z), а остальные 5 силовых факторов равны нулю (Qx=Qy=Mx=My=Mz=0). Правило знаков для Nz: истинная растягивающая сила – «+», истинная сжимающая сила – «-». Центральное растяжение (сжатие) прямого бруса. Постановка и решение задачи об определении напряжений в поперечных сечениях бруса. Три стороны задачи. Центральное напряжение (сж.) прямого бруса см. в вопросе 8. Постановка: Прямой брус из однородного материала, растянутый (сжатый) центральными продольными силами N. Определить напряжение, возникающее в поперечных сечениях бруса, деформации и перемещения поперечных сечений бруса в зависимости от координат z этих сечений. megaobuchalka.ru Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.). Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим∆R . Полное среднее напряжение на этой площадке р =∆R ∆A . Найдем предел этого отношения при ∆A 0 . Это и будет полным напряжение на данной площадке (точке) тела. p =lim A 0 A R Полное напряжение p , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение n. Здесь n – нормаль к выделенной площадке1. Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – nx ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения. p = n nx nx . Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением p , а с его составляющимиσx xy xz . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ. Тензор напряжений При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σx xy xz Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей –тензором напряженийT = x xy xz yx y yz zx zy z Здесь первый столбец представляет компоненты напряжений на площадках,нормальных к оси x, второй и третий – к оси y и z соответственно. При повороте осей координат, совпадающих с нормалями к граням выделенногоэлемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю. Площадка, на которой касательные напряжения равны нулю, называется главной площадкой. Нормальное напряжение на главной площадке называется главным напряжением Нормаль к главной площадке называется главной осью напряжений . В каждой точке можно провести три взаимно-перпендикулярных главных площадки. При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС). Связь внутренних усилий и напряжений Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению. Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать: Продольное усилие на площадке dA: dN = σzdAПоперечная сила вдоль оси х: dQ x = zx dAПоперечная сила вдоль оси y: dQ y = zy dAЭлементарные моменты вокруг осей x,y,z: dMx=σzdA y dMy=σzdA x dMz=dMk= zydA x− zxdA y Выполнив интегрирование по площади поперечного сечения получим: То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела. megaobuchalka.ru Напряжение касательное полное – проекция полного напряжения на касательную плоскость в данной точке. [Словарь основных терминов, необходимых при проектировании, строительстве и эксплуатации автомобильных дорог. Москва 1967] Рубрика термина: Деформации материалов Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги, Автотехника, Автотранспорт, Акустические материалы, Акустические свойства, Арки, Арматура, Арматурное оборудование, Архитектура, Асбест, Аспирация, Асфальт, Балки, Без рубрики, Бетон, Бетонные и железобетонные, Блоки, Блоки оконные и дверные, Бревно, Брус, Ванты, Вентиляция, Весовое оборудование, Виброзащита, Вибротехника, Виды арматуры, Виды бетона, Виды вибрации, Виды испарений, Виды испытаний, Виды камней, Виды кирпича, Виды кладки, Виды контроля, Виды коррозии, Виды нагрузок на материалы, Виды полов, Виды стекла, Виды цемента, Водонапорное оборудование, Водоснабжение, вода, Вяжущие вещества, Герметики, Гидроизоляционное оборудование, Гидроизоляционные материалы, Гипс, Горное оборудование, Горные породы, Горючесть материалов, Гравий, Грузоподъемные механизмы, Грунтовки, ДВП, Деревообрабатывающее оборудование, Деревообработка, ДЕФЕКТЫ, Дефекты керамики, Дефекты краски, Дефекты стекла, Дефекты структуры бетона, Дефекты, деревообработка, Деформации материалов, Добавки, Добавки в бетон, Добавки к цементу, Дозаторы, Древесина, ДСП, ЖД транспорт, Заводы, Заводы, производства, цеха, Замазки, Заполнители для бетона, Защита бетона, Защита древесины, Защита от коррозии, Звукопоглащающий материал, Золы, Известь, Изделия деревянные, Изделия из стекла, Инструменты, Инструменты геодезия, Испытания бетона, Испытательное оборудование, Качество цемента, Качество, контроль, Керамика, Керамика и огнеупоры, Клеи, Клинкер, Колодцы, Колонны, Компрессорное оборудование, Конвеера, Конструкции ЖБИ, Конструкции металлические, Конструкции прочие, Коррозия материалов, Крановое оборудование, Краски, Лаки, Легкие бетоны, Легкие наполнители для бетона, Лестницы, Лотки, Мастики, Мельницы, Минералы, Монтажное оборудование, Мосты, Напыления, Обжиговое оборудование, Обои, Оборудование, Оборудование для производства бетона, Оборудование для производства вяжущие, Оборудование для производства керамики, Оборудование для производства стекла, Оборудование для производства цемента, Общие, Общие термины, Общие термины, бетон, Общие термины, деревообработка, Общие термины, оборудование, Общие, заводы, Общие, заполнители, Общие, качество, Общие, коррозия, Общие, краски, Общие, стекло, Огнезащита материалов, Огнеупоры, Опалубка, Освещение, Отделочные материалы, Отклонения при испытаниях, Отходы, Отходы производства, Панели, Паркет, Перемычки, Песок, Пигменты, Пиломатериал, Питатели, Пластификаторы для бетона, Пластифицирующие добавки, Плиты, Покрытия, Полимерное оборудование, Полимеры, Половое покрытие, Полы, Прессовое оборудование, Приборы, Приспособления, Прогоны, Проектирование, Производства, Противоморозные добавки, Противопожарное оборудование, Прочие, Прочие, бетон, Прочие, замазки, Прочие, краски, Прочие, оборудование, Разновидности древесины, Разрушения материалов, Раствор, Ригеля, Сваи, Сваизабивное оборудование, Сварка, Сварочное оборудование, Свойства, Свойства бетона, Свойства вяжущих веществ, Свойства горной породы, Свойства камней, Свойства материалов, Свойства цемента, Сейсмика, Склады, Скобяные изделия, Смеси сухие, Смолы, Стекло, Строительная химия, Строительные материалы, Суперпластификаторы, Сушильное оборудование, Сушка, Сушка, деревообработка, Сырье, Теория и расчет конструкций, Тепловое оборудование, Тепловые свойства материалов, Теплоизоляционные материалы, Теплоизоляционные свойства материалов, Термовлажносная обработка бетона, Техника безопасности, Технологии, Технологии бетонирования, Технологии керамики, Трубы, Фанера, Фермы, Фибра, Фундаменты, Фурнитура, Цемент, Цеха, Шлаки, Шлифовальное оборудование, Шпаклевки, Шпон, Штукатурное оборудование, Шум, Щебень, Экономика, Эмали, Эмульсии, Энергетическое оборудование Источник: Энциклопедия терминов, определений и пояснений строительных материалов Энциклопедия терминов, определений и пояснений строительных материалов. - Калининград. Под редакцией Ложкина В.П.. 2015-2016. construction_materials.academic.ruЛекции и примеры решения задач механики. Полное напряжение
Полное напряжение - Большая Энциклопедия Нефти и Газа, статья, страница 1
Полное напряжение
Внутненние силы в поперечном сечении


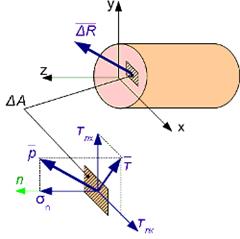 Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим∆R
Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим∆R  . Полное среднее напряжение на этой площадке р
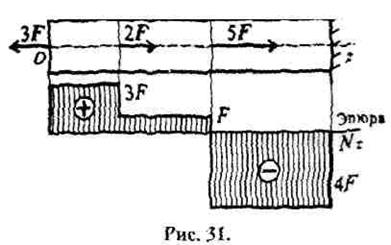
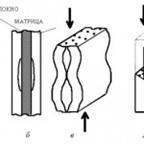
. Полное среднее напряжение на этой площадке р  =∆R
=∆R 
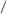 ∆A . Найдем предел этого отношения при ∆A
∆A . Найдем предел этого отношения при ∆A  0 . Это и будет полным напряжение на данной площадке (точке) тела.
0 . Это и будет полным напряжение на данной площадке (точке) тела. =lim
=lim  A
A 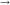 0
0  A
A  R
R 
 , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение
, как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение  n. Здесь n – нормаль к выделенной площадке1.
n. Здесь n – нормаль к выделенной площадке1. nx
nx 
 ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.
ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения. =
= 

 n
n  nx
nx  nx
nx 

 , а с его составляющими σx
, а с его составляющими σx 
 xy
xy 
 xz . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.
xz . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.

Сопромат.in.ua: Напряжения
 Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.
Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела. Тензор напряжений
 При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – [math]σ_x,\tau _{xy}, \tau _{xz} [/math]
При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – [math]σ_x,\tau _{xy}, \tau _{xz} [/math] Связь внутренних усилий и напряжений
 Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:
Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать: 
Связанные статьи
Напряженное состояние и гипотезы прочности
Понятие о напряжениях в точке

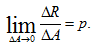
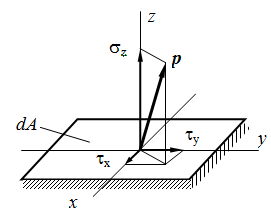
Связь между напряжениями и внутренними силами
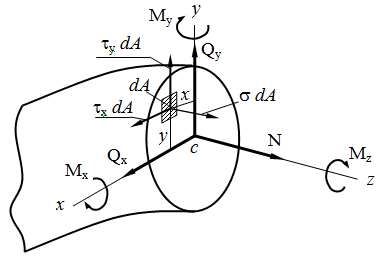
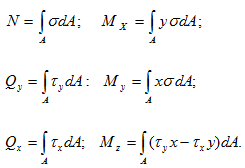
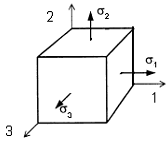
Объемное напряженное состояние
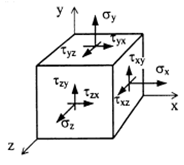
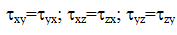
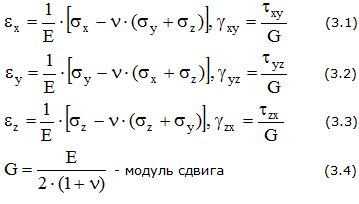
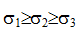
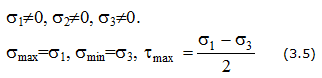
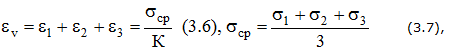
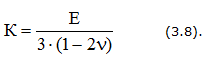
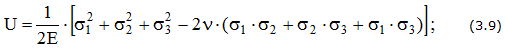
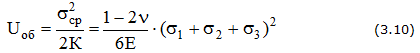
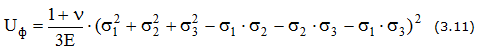
Плоское напряженное состояние
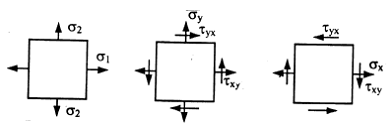
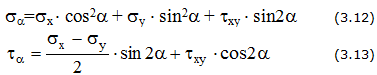
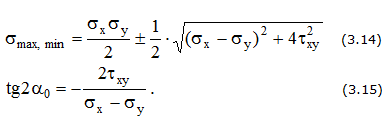
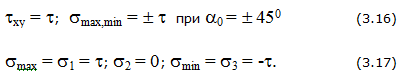
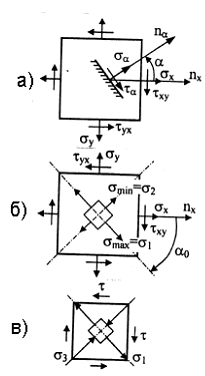
Линейное напряженное состояние
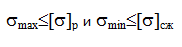
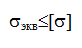
Гипотезы прочности
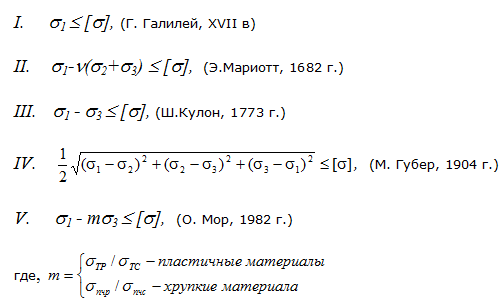
Напряжение в точке. Полное, нормальное, касательное напряжения. Размерности напряжения
Напряжение: нормальное, касательное — Мегаобучалка
Напряжение касательное полное - это... Что такое Напряжение касательное полное?
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''








Поделиться с друзьями: