Разность Потенциалов электрическая электрическое( напряжение) между двумя точками - равна работе электрического поля по перемещению единичного положительного заряда из одной точки поля в другую. Электродвижущая сила (ЭДС)— физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. ЭДС можно выразить через напряжённость электрического поля сторонних сил (Eex). В замкнутом контуре (L) тогда ЭДС будет равна: ,где dl — элемент длины контура. ЭДС так же, как и напряжение, измеряется в вольтах. электрическое напряжениеэто физическая величина численно равная отношению работы , совершенной при переносе заряда между двумя точками электрического поля и величины этого заряда . Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления. Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как где R — сопротивление; U — разность электрических потенциалов на концах проводника; I — сила тока, протекающего между концами проводника под действием разности потенциалов. Сопротивление R однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины и сечения следующим образом: где ρ — удельное сопротивление вещества проводника, L — длина проводника, а S — площадь сечения. Величина, обратная удельному сопротивлению называется удельной проводимостью. Эта величина связана с температурой формулой Нернст-Эйнштейна: где T — температура проводника; D — коэффициент диффузии носителей заряда; Z — количество электрических зарядов носителя; e — элементарный электрический заряд; C — Концентрация носителей заряда; kB — постоянная Больцмана. Следовательно, сопротивление проводника связано с температурой следующим соотношением: Сверхпроводи́мость— свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). Простейшая разветвленная цепь. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году. Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком): Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины. Второй закон Кирхгофа(Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю: для постоянных напряжений для переменных напряжений Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Пример Например, для приведённой на рисунке цепи, в соответствии с первым закономвыполняются следующие соотношения: Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными. В соответствии со вторым законом, справедливы соотношения: studfiles.net Сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на заряд каждый из зарядов системы в отдельности (принцип суперпозиции). Тогда A = ∑Ai Здесь каждое слагаемое не зависит от формы пути и, следовательно не зависит от формы пути и сумма. Итак электростатическое поле потенциально. Работу сил электростатического поля можно выразить через убыль потенциальной энергии – разность двух функций состояния: A12= Eп1– Eп2 (3.2.2) Тогда выражение (3.2.2) можно переписать в виде: A12= qq' − qq' (3.2.3) 4πεε r 4πεε r 0 1 0 2 Сопоставляя формулу (3.2.2) и (3.2.3) получим выражение для потенциальной энергии заряда q' в поле зарядаq: 1 qq' En= +const (3.2.4) 4πεε0 r Потенциальную энергию определяют с точностью до постоянной интегрирования. Значение константы в выражении Eпот. выбирают таким образом, чтобы при удалении заряда на бесконечность (т. е. приr = ∞), потенциальная энергия обращалась в нуль. Выражение (3.2.4.) – для одного заряда. Для системы зарядов EnΣ= ∑Eni (3.2.5) Разные пробные заряды q',q'',… будут обладать в одной и той же точке поля разными энергиямиEn', En'' и так далее. Однако отношениеEn/q'пр. будет для всех зарядов одним и тем же.Поэтому ввели скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал. φ= En (3.3.1) q' Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Подставив в (3.3.1.) значение потенциальной энергии (3.2.3), получим для потенциала точечного заряда следующее выражение: φ= 1 q (3.3.2) 4πεε0 r Потенциал, как и потенциальная энергия, определяют с точностью до постоянной интегрирования. Договорились считать, что потенциал точки удаленной в бесконечность равен нулю. Поэтому когда говорят «потенциал такой-тоточки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность. Другое определение потенциала: φ = Aq∞ или A∞ = qφ, т.е. потенциал числено равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность dA = Fl dl = El qdl (наоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля. Если поле создается системой зарядов, то, используя принцип суперпозиции, получим: 1 N qi q' En= ∑= (3.3.3) 4πεε r 0 i 1 i Тогда: 1 qi φ= ∑φi φ= ∑ (3.3.4) 4πεε r 0 i т.е. потенциал поля, создаваемый системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. А вот напряженности, как вы помните, складываются при наложении полей –векторно. По этой причине потенциалы полей считать проще, чем напряженности. Вернемся к работе сил электростатического поля над зарядом q'. Выразим работу через разность потенциалов: A12= En1− En2= φ1q′−φ2q′ = q′(φ1−φ2) (3.3.5) Т.о., работа над зарядом q' равна произведению заряда на убыль потенциала. То есть: A = q'(φ1 −φ2 )= q'U, A = qU, (3.3.6) где U – разность потенциалов или еще называютнапряжение. Между прочим, хорошая аналогия: A12 = mgh2 −mgh3 = m(gh2 − gh3 ) gh – имеет смысл потенциала гравитационного поля, а m – заряд. Итак потенциал – скалярная величина, поэтому пользоваться и вычислять φ проще, чем E . Приборы для измерения разности потенциалов широко распространены. ФормулуA∞=qφ можно использовать для установления единиц потенциала:за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из ∞ единичного положительного заряда необходимо совершить работу равную единице. Так в СИ – единица потенциала 1В = 1Дж/1Кл, в СГСЭ 1ед.пот. = 300В. В физике часто используется единица энергии и работы, называемой эВ – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1В, то есть: 1эВ =1,6 10−19 Кл В =1,6 10−19 Дж Итак электростатическое поле можно описать либо с помощью векторной величины E , либо с помощью скалярной величиныφ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее: Изобразим перемещение заряда q по произвольному путиl. Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl можно найти так: (3.4.1) El – проекцияE наdrl ;dl – произвольное направление перемещения заряда. С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl. dA = −qdφ; El qdl= −qdφ (3.4.2) El = − dφ (3.4.3) dl Вот отсюда размерность напряженности поля В/м. Для ориентации dl – (направление перемещения) в пространстве, надо знать проекцииE на оси координат: Ex = − ∂φ ; Ey = −∂φ ; Ez = − ∂φ ; (3.4.4) ∂x ∂y ∂z r ∂φr − ∂φr ∂φ r (3.4.5) E = − ∂x i ∂y j − ∂z k где i,j,k – орты осей – единичные вектора. По определению градиента сумма первых производных от какой-либофункции по координатам есть градиент этой функции, то есть: gradφ = ∂∂φx ri + ∂∂φy rj + ∂∂φz kr Тогда коротко записывается так: E = −gradφ (3.4.6) gradφ – вектор, показывающий направление наибыстрейшего увеличения функции. Знак минус говорит о том, что E направлен в сторону уменьшения потенциала электрического поля. Как мы с вами уже знаем, направление силовой линии (линии напряженности) в каждой точке совпадает с направлением E .Отсюда следует, что напряженность E равна разности потенциалов на единицу длины силовой линии. Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить E между двумя точками, измеряяU между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии – прямые. Поэтому здесь определение E наиболее просто: E = U В (3.5.1) l м Теперь запишем определение эквипотенциальной поверхности.Воображаемая поверхность все точки, которой имеют одинаковый потенциал, называют эквипотенциальной поверхностью. Уравнение этой поверхности φ =φ (x,y,z) = const. (3.5.2) Рис. 3.4 При перемещении по этой поверхности на dl, потенциал не изменится:dφ = 0. Следовательно, проекция вектораE наdl равна0, то естьEl = 0. Отсюда следует, что E в каждой точкенаправлена по нормали к эквипотенциальной поверхности. Эквипотенциальных поверхностей можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине E , это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине. На одной из лабораторных работах мы с вами будем моделировать электрическое поле и находить эквипотенциальные поверхности и силовые линии от электродов различной формы – очень наглядно вы увидите как могут располагаться эквипотенциальные поверхности. Формула E = −gradφ – выражает связь потенциала с напряженностью и позволяет по известным значениямφ найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по известным значениям E в каждой точке поля найти разностьφ между двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядомq при перемещении его из точки 1 в точку 2, может быть, вычислена как: 2 r r A12 = ∫qEdl 1 С другой стороны работу можно представить в виде: A12= q(φ1−φ2) тогда 2 r r φ1−φ2= ∫Edl (3.5.3) 1 Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру φ1 = φ2 получим: т.е. пришли к известной нам теореме о циркуляции вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее этим свойством, называется потенциальным. Из обращения в нуль циркуляции вектора E , следует, что линии E электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах и на отрицательных зарядах заканчиваются или уходят в бесконечность. 31 studfiles.net Понятие «потенциал» широко используется в физике для характеристики различных полей и сил. Наиболее известны такие применения: Разность потенциалов В свою очередь, электромагнитный делится на два понятия: Напряженность изменяющегося электрического поля находится через электрический потенциал, в то время как статичное поле характеризуется электростатическим. Разность потенциалов, или напряжение, – одно из основных понятий электротехники. Ее можно определить как работу электрического поля, затраченную на перенос заряда между двумя точками. Тогда на вопрос, что такое потенциал, можно ответить, что это работа по переносу единичного заряда из данной точки в бесконечность. Как и в случае гравитационных сил, заряд, подобно телу с потенциальной энергией, имеет определенный электрический потенциал при внесении его в электрическое поле. Чем выше напряженность электрического поля, и больше величина заряда, тем выше его электрический потенциал. Для определения напряжения существует формула: U=A/q, которая связывает работу А по перемещению заряда q из одной точки в другую. Проведя преобразование, получим: А=Uq. То есть чем выше напряжение, тем большую работу электрическим полем (электричеством) надо затратить по переносу зарядов. Данное определение позволяет понять суть мощности источника питания. Чем выше его напряжение, разность потенциалов между клеммами, тем большее количество работы он может обеспечить. Разность потенциалов измеряется в вольтах. Для измерения напряжения созданы измерительные приборы, которые именуются вольтметрами. Они основаны на принципах электродинамики. Ток, проходя по проволочной рамке вольтметра, под действием измеряемого напряжения создает электромагнитное поле. Рамка находится между полюсами магнитов. Взаимодействие полей рамки и магнита заставляет последнюю отклониться на некоторый угол. Большая разность потенциалов создает больший ток, в результате угол отклонения увеличивается. Шкала прибора пропорциональна углу отклонения рамки, то есть разности потенциалов и проградуирована в вольтах. Вольтметр В руках современного электрика имеются не только стрелочные, но и цифровые измерительные приборы, которые не только измеряют электрический потенциал в определенной точке схемы, но и другие величины, характеризующие электрическую цепь. Напряжения в точках измеряются по отношению к другим, которым условно присваивают значение нуля. Тогда измеренное значение между нулевым и потенциальным выводами даст искомое напряжение. Сказанное выше относится к напряжению как разности потенциалов между двумя зарядами. В электротехнике эта разность измеряется на участке цепи при протекании по нему тока. В случае переменного тока, то есть изменяющего во времени амплитуду и полярность, напряжение в цепи изменяется по такому же закону. Это справедливо только при наличии в схеме активных сопротивлений. Реактивные элементы в цепи переменного тока вызывают сдвиг фазы относительно протекающего тока. Напряжение источников питания, в особенности автономных, таких как аккумуляторы, химические источники, солнечные и тепловые батареи, является постоянным и не поддается регулировке. Для получения меньших значений используются, в простейшем случае, потенциометрические делители напряжения с использованием трехвыводного переменного резистора (потенциометра). Как работает потенциометр? Переменный резистор представляет собой резистивный элемент с двумя выводами, по которому может перемещаться контактный ползунок с третьим выводом. Потенциометр-реостат Переменный резистор может включаться двумя способами: В первом случае у переменного резистора используются два вывода: один – основной, другой – с ползунка. Перемещая ползунок по телу резистора, изменяют сопротивление. Включив реостат в цепь электрического тока последовательно с источником напряжения, можно регулировать ток в цепи. Реостатное включение Включение потенциометром требует использования всех трех выводов. Основные выводы подключаются параллельно источнику питания, а пониженное напряжение снимается с ползунка и одного из выводов. Принцип действия потенциометра заключается в следующем. Через резистор, подключенный к источнику питания, проходит ток, который создает падение напряжения между ползунком и крайними выводами. Чем меньше сопротивление между ползунком и выводом, тем меньше напряжение. Данная схема имеет недостаток, она сильно нагружает источник питания, поскольку для корректной и точной регулировки требуется, чтобы сопротивление переменного резистора было в несколько раз меньше сопротивления нагрузки. Потенциометрическое включение Обратите внимание! Название «потенциометр» в данном случае не совсем корректно, поскольку из названия следует, что это устройство для измерения, но так как по принципу действия оно схоже с современным переменным резистором, то это название за ним прочно закрепилось, особенно в любительской среде. Многие понятия в физике схожи и могут служить примером друг другу. Это справедливо и для такого понятия, как потенциал, который может быть как механической величиной, так и электрической. Сам по себе потенциал измерить невозможно, поэтому речь идет о разности, когда один из двух зарядов принимается за точку отсчета – нуль или заземление, как принято в электротехнике. elquanta.ru Электростатическое поле обладает энергией. Если в электростатическом поле находится электрический заряд, то поле, действуя на него с некоторой силой, будет его перемещать, совершая работу. Всякая работа связана с изменением какого - то вида энергии. Работу электростатического поля по перемещению заряда принято выражать через величину, называемую разностью потенциалов. где q - величина перемещаемого заряда, j1 и j2 - потенциалы начальной и конечной точек пути. Для краткости в дальнейшем будем обозначать A = qV. V = A/q. РАЗНОСТЬ ПОТЕНЦИАЛОВ МЕЖДУ ТОЧКАМИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ - ЭТО РАБОТА, КОТОРУЮ СОВЕРШАЮТ ЭЛЕКТРИЧЕСКИЕ СИЛЫ ПРИ ПЕРЕМЕЩЕНИИ МЕЖДУ НИМИ ЗАРЯДА В ОДИН КУЛОН. [V] = В. 1 вольт - это разность потенциалов между точками, при перемещении между которыми заряда в 1 кулон, электростатические силы совершают работу в 1 джоуль. Разность потенциалов между телами измеряют электрометром, для чего одно из тел соединяют проводниками с корпусом электрометра, а другое - со стрелкой. В электрических цепях разность потенциалов между точками цепи измеряют вольтметром. С удалением от заряда электростатическое поле ослабевает. Следовательно, стремится к нулю и энергетическая характеристика поля - потенциал. В физике потенциал бесконечно удалённой точки принимается за ноль. В электротехнике же считают, что нулевым потенциалом обладает поверхность Земли. Если заряд перемещается из данной точки в бесконечность, то A = q(j - O) = qj => j= A/q, т.е. ПОТЕНЦИАЛ ТОЧКИ - ЭТО РАБОТА, КОТОРУЮ НАДО СОВЕРШИТЬ ЭЛЕКТРИЧЕСКИМ СИЛАМ, ПЕРЕМЕЩАЯ ЗАРЯД В ОДИН КУЛОН ИЗ ДАННОЙ ТОЧКИ В БЕСКОНЕЧНОСТЬ. Пусть в однородном электростатическом поле с напряженностью E перемещается положительный заряд q вдоль направления вектора напряженности на расстояние d. Работу поля по перемещению заряда можно найти и через напряженность поля и через разность потенциалов. Очевидно, что при любом способе вычисления работы получается одна и та же ее величина. A = Fd = Eqd = qV. => E = V/d. Эта формула связывает между собой силовую и энергетическую характеристики поля. Кроме того, она дает нам единицу напряженности. [E] = В/м. 1 В/м - это напряженность такого однородного электростатического поля, потенциал которого изменяется на 1 В при перемещении вдоль направления вектора напряженности на 1 м. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. Увеличение разности потенциалов на концах проводника вызывает увеличение силы тока в нем. Ом экспериментально доказал, что сила тока в проводнике прямо пропорциональна разности потенциалов на нем. При включении разных потребителей в одну и ту же электрическую цепь сила тока в них различна. Значит разные потребители по - разному препятсявуют прохождению по ним электрического тока. ФИЗИЧЕСКАЯ ВЕЛИЧИНА, ХАРАКТЕРИЗУЮЩАЯ СПОСОБНОСТЬ ПРОВОДНИКА ПРЕПЯТСТВОВАТЬ ПРОХОЖДЕНИЮ ПО НЕМУ ЭЛЕКТРИЧЕСКОГО ТОКА, НАЗЫВАЕТСЯ ЭЛЕКТРИЧЕСКИМ СОПРОТИВЛЕНИЕМ. Сопротивление данного проводника - это постоянная величина при постоянной температуре. При повышении температуры сопротивление металлов возрастает, жидкостей - падает. [R] = Ом. 1 Ом - это сопротивление такого проводника, по которому течет ток 1 А при разности потенциалов на его концах 1В. Чаще всего используются металлические проводники. Носителями тока в них являются свободные электроны. При движении по проводнику они взаимодействуют с положительными ионами кристаллической решетки, отдавая им часть своей энергии и теряя при этом скорость. Для получения нужного сопротивления используют магазин сопротивлений. Магазин сопротивлений представляет собой набор проволочных спиралей с известными сопротивлениями, которые можно включать в цепь в нужной комбинации. Ом экспериментально установил, что СИЛА ТОКА В ОДНОРОДНОМ УЧАСТКЕ ЦЕПИ ПРЯМО ПРОПОРЦИОНАЛЬНА РАЗНОСТИ ПОТЕНЦИАЛОВ НА КОНЦАХ ЭТОГО УЧАСТКА И ОБРАТНО ПРОПОРЦИОНАЛЬНА СОПРОТИВЛЕНИЮ ЭТОГО УЧАСТКА. Однородным участком цепи называется участок, на котором нет источников тока. Это закон Ома для однородного участка цепи - основа всех электротехнических расчетов. Включая проводники разной длины, разного поперечного сечения, сделанные из разных материалов, было установлено: СОПРОТИВЛЕНИЕ ПРОВОДНИКА ПРЯМО ПРОПОРЦИОНАЛЬНО ДЛИНЕ ПРОВОДНИКА И ОБРАТНО ПРОПОРЦИОНАЛЬНО ПЛОЩАДИ ЕГО ПОПЕРЕЧНОГО СЕЧЕНИЯ. СОПРОТИВЛЕНИЕ КУБА С РЕБРОМ В 1 МЕТР, СДЕЛАННОГО ИЗ КАКОГО - ТО ВЕЩЕСТВА, ЕСЛИ ТОК ИДЕТ ПЕРЕПЕНДИКУЛЯРНО ЕГО ПРОТИВОПОЛОЖНЫМ ГРАНЯМ, НАЗЫВАЕТСЯ УДЕЛЬНЫМ СОПРОТИВЛЕНИЕМ ЭТОГО ВЕЩЕСТВА. [r] = Ом м. Часто используется и несистемная единица удельного сопротивления - сопротивление проводника с площадью поперечного сечения 1 мм2 и длиной 1 м. [r]=Ом мм2/м. Удельное сопротивление вещества - табличная величина. Сопротивление проводника пропорционально его удельному сопротивлению. R=rL/S. На зависимости сопротивления проводника от его длины основано действие ползунковых и ступенчатых реостатов. Ползунковый реостат представляет собой керамический цилиндр с намотанной на него никелиновой проволокой. Подключение реостата в цепь осуществляется с помощью ползуна, включающего в цепь большую или меньшую длину обмотки. Проволока покрывается слоем окалины, изолирующей витки друг от друга. А)ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПОТРЕБИТЕЛЕЙ. Часто в электрическую цепь включается несколько потребителей тока. Это связано с тем, что не рационально иметь у каждого потребителя свой источник тока. Существует два способа включения потебителей: последовательное и параллельное, и их комбинации в виде смешанного соединения. а) Последовательное соединение потребителей. При последовательном соединении потебители образуют непрерывную цепочку, в которой потребители соединяются друг за другом. При последовательном соединении нет ответвлений соединительных проводов. Рассмотрим для простоты цепь из двух последовательно соединенных потребителей. Электрический заряд, прошедший через один из потребителей, пройдет и через второй, т.к. в проводнике, соединяющем потребители не может быть исчезновения, возникновения и накапливания зарядов. q=q1=q2. Разделив полученное уравнение на время прохождения тока по цепи, получим связь между током, протекающим по всему соединению, и токами, протекающими по его участкам. I=I1=I2 (1). Очевидно, что работа по перемещению единичного положительного заряда по всему соединению слагается из работ по перемещению этого заряда по всем его участкам. Т.е. V=V1+V2 (2). Общая разность потенциалов на последовательно соединенных потребителях равна сумме разностей потенциалов на потребителях. Разделим обе части уравнения (2) на силу тока в цепи, получим: U/I=V1/I+V2/I. Т.е. сопротивление всего последовательно соединенного участка равно сумме сопротивлений потебителей его составляющих. R=R1+R2 (3). Б) Паралельное соединение потребителей. Это самый распространенный способ включения потребителей. При этом соединении все потребители включаются на две общие для всех потребителей точки. При прохождении параллельного соединения, электрический заряд, идущий по цепи, делится на несколько частей, идущих по отдельным потребителям. По закону сохранения заряда q=q1+q2. Разделив данное уравнение на время прохождения заряда, получим связь между общим током, идущим по цепи, и токами, идущими по отдельным потребителям. I=I1+I2 (1). В соответствии с определением разности потенциалов V=V1=V2 (2). По закону Ома для участка цепи заменим силы токов в уравнении (1) на отношение разности потенциалов к сопротивлению. Получим: V/R=V/R1+V/R2. После сокращения: 1/R=1/R1+1/R2, т.е. величина, обратная сопротивлению параллельного соединения, равна сумме величин, обратных сопротивлениям отдельных его ветвей. Читайте также: lektsia.com Наряду с напряжённостью, для характеристики электростатического поля вводят ещё одну физическую величину, называемую потенциалом, которая является энергетической характеристикой этого поля. Она равна (1) т.е. потенциалом электростатического поля называется отношение потенциальной энергии, которой обладает заряд в некоторой точке поля, к величине этого заряда. Разность потенциалов находится по формуле: (2) т.е. разностью потенциалов электростатического поля называется отношение работы, совершаемой силами поля при перемещении заряда из одной точки поля в другую, к величине этого заряда. В системе единиц СИ потенциал и разность потенциалов измеряется в вольтах (B). Электростатическое поле характеризуется двумя физическими величинами напряжённостью и потенциалом. Они связаны между собой соотношением: (3) т.е. проекция напряжённости на какое-либо направление в каждой точке поля равна производной потенциала по данному направлению, взятой с противоположным знаком. Знак минус в выражении (3) указывает на то, что напряжённость в любой точке поля направлена в сторону убывания потенциала. Из формулы (3) можно найти разность потенциалов 1 – 2 между токами, находящимися в однородном электростатическом поле на расстоянии d по линии напряжённости: (4) Электроёмкостью С конденсатора называется отношение заряда q на конденсаторе к разности потенциалов 1 – 2 между его обкладками: (5) В системе СИ ёмкость измеряется в фарадах. Процесс возникновения разноимённых зарядов на обкладках конденсатора можно представить так, что от одной обкладки отнимается некоторый заряд и передаётся другой. Пусть разность потенциалов между обкладками в какой-то момент времени равна 1 2. Тогда при перемещении элементарного заряда dq изменением этой разности потенциалов можно пренебречь, и элементарная работа dA по переносу данного заряда равна dA = (1 2)dq. Полная работа, необходимая для сообщения конденсатору заряда q, находится по формуле Используя формулу ёмкости конденсатора, находим, что1 2 = q/C, где C — ёмкость конденсатора. Тогда Очевидно, что электрическая энергияWE заряженного конденсатора равна этой работе, т.е. WE = q2/(2C). (6) Учитывая, что q = (1 2)C, выражение (5) запишем в ином виде WE = (1/2)C(1 2)2. (7) Энергия заряженных проводников запасена в виде электрического поля. Поэтому целесообразно выразить её через напряжённость, характеризующую это поле. Это проще всего проделать для плоского конденсатора. В этом случае 1 2 = Ed, где d — расстояние между обкладками, и C = 0 S/d. Здесь 0 — электрическая постоянная, — диэлектрическая проницаемость диэлектрика, заполняющего конденсатор, d — расстояние между обкладками конденсатора, S — площадь каждой обкладки. Подставляя эти выражения в (7), получаем WE = (1/2)0E2V. (8) Здесь V = Sd — объём, занимаемый полем, равный объёму конденсатора. Введём понятие объёмной плотности энергии. Пусть энергия поля WE равномерно распределена по объёму V. Тогда объёмная плотность wE энергии равна: wE = WE /V, (9) т.е. объёмная плотность энергии —это энергия поля в единице объёма. В случае конденсатора, заполненного диэлектриком, объёмная плотность энергии, как следует из (7) и (8), находится по формуле (10) В заключении отметим, что эта формула справедлива не только для конденсатора, но и для других электрических полей, в том числе и для переменных. studfiles.net Работа получается положительной, так как сила и перемещение сонаправлены. C другой стороны, работа поля есть произведение заряда на разность потенциалов между точками 1 и 2: A = qU: (Напряжение также положительно, так как '1 > '2 ведь напряжённость направлена в сторону убывания потенциала.) Приравнивая правые части последних двух формул, получим: qU = qEd, откуда Эта простая формула позволяет находить напряжение между точками однородного поля E, находящимися на одной силовой линии; при этом напряжённость поля направлена от начальной точки к конечной. Выразим из формулы (21) напряжённость: E = U : (22) d Эта формула пригодится нам впоследствии, при нахождении напряжённости поля в конденсаторе. А сейчас обратим внимание на одно следствие данной формулы: единицей измерения напряжённости является В/м. Эта единица используется чаще, чем первоначальная Н/Кл. Что ж, немало вещей пришлось узнать, чтобы понять равенство Н/Кл = В/м :-) Как вы помните, введение силовой характеристики поля (напряжённости) дало возможность изображать поле графически в виде картины линий напряжённости, или силовых линий. Энергетическая характеристика поля (потенциал) также позволяет дать графическую картину поля в виде семейства эквипотенциальных поверхностей. Поверхность в пространстве называется эквипотенциальной, если во всех точках этой поверхности потенциал электрического поля принимает одно и то же значение. Коротко говоря, эквипотенциальные поверхности это поверхности равного потенциала. Например, из формулы ' = Ex мы видим, что эквипотенциальными поверхностями однородного поля являются всевозможные плоскости x = const. Они перпендикулярны линиям напряжённости. Так, на рис. 21 изображены пять плоскостей эквипотенциальных поверхностей, отвечающих значениям потенциала '1, '2, '3, '4 и '5. E '1'2'3'4'5 Рис. 21. Эквипотенциальные поверхности однородного поля Теперь рассмотрим нашу вторую стандартную ситуацию: поле точечного заряда q > 0. Потенциал этого поля, как мы уже видели, равен: ' = kqr : studfiles.netЛекция №5 потенциал и разность потенциалов электростатического поля. Разность потенциалов через напряжение
разность потенциалов, электродвижущая сила, напряжение, сопротивление. Зависимость сопротивления от температуры. Сверхпроводимость.
47.Разветвленные цепи. Правила Кирхгофа и их физическое содержание.
3.3. Потенциал. Разность потенциалов.
3.4. Связь между напряженностью и потенциалом.
3.5. Силовые линии и эквипотенциальные поверхности.
разность потенциалов в электротехнике и физике
Разность потенциалов
Потенциометры
Видео
Оцените статью: ПОТЕНЦИАЛ. РАЗНОСТЬ ПОТЕНЦИАЛОВ.
⇐ ПредыдущаяСтр 4 из 6Следующая ⇒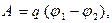 ,
, . V - разность потенциалов.
. V - разность потенциалов. .
.Лекция №5 потенциал и разность потенциалов электростатического поля
Связь между напряжённостью и потенциалом
Конденсаторы
Энергия заряженного конденсатора
Энергия электрического поля.
Разность потенциалов
4.9Эквипотенциальные поверхности
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''








Поделиться с друзьями: