Основные гипотезы о деформируемом теле. Примеры использования гипотез в расчётах напряжений, деформаций, перемещений. = Гипотеза сплошности и непрерывности материала. Материал сплошной (непрерывный). = Гипотеза однородности свойств материала по всему объёму (макроскопическая гипотеза). = Гипотеза изотропности. Во всех направлениях свойства одинаковы. = Гипотеза естественного состояния материала. Основные принципы, упрощающие расчёт моделей объектов. Примеры применения этих принципов в прочностных расчётах. = Принцип мгновенного отвердевания (принцип неизменности начальных размеров деформированной системы). При определении опорных реакций или каких-либо неизвестных сил из условий равновесия, считается, что под действием приложенных усилий, размеры конструкции не изменяются. = Принцип освобождаемости (от связей, наложенных на систему). Усилия, действующие на конструкцию со стороны других систем через связи в виде опор, учитываются в уравнение равновесия без конструктивных особенностей этих других систем (все системы, действующие на данную систему, заменяются соответствующими усилиями, действующими по месту приложения). = Принцип независимости действия сил. Последовательность приложения (порядок приложения) сил (усилий) к данной конструкции даёт один и тот же результат, как и другой порядок приложения к той же самой системе сил. = Принцип суперпозиции (наложения). Результат действия системы сил на конструкцию равен сумме результатов действий каждого из этих сил на конструкцию. = Принцип Сен-Венана. Для однородного стержня вынужденные силы распределены по сечению равномерно, так как из рассмотрения исключаются особенности конкретно взятого стержня в условиях его закрепления на концах. 3. Классификация сил (нагрузок) и объектов, изучаемых в курсе сопротивления материалов. Размерности нагрузок. Силы: Усилия, приложенные к данному телу, сила распределённой нагрузки, моменты, сила гравитации, сила инерции. Объекты: Тонкий стержень, оболочка, массив, тонкостенный стержень. Основные понятия о деформируемом теле: линейные и угловые перемещения и деформации; упругость, пластичность, хрупкость; изотропия и анизотропия. Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки образует деформированное состояние в точке. Упругость – свойство тела восстанавливать свои первоначальные размеры. Пластичность – способность материала получать большие остаточные деформации. Хрупкость – способность материала разрушаться без образования заметных остаточных перемещений. Изотропность – свойства любого тела, выделенного из сплошной среды не зависят от его исходной ориентации в пределах этой среды. (Изотр.: металлы, анизотр.: дерево, бумага). 5. Метод сечений для определения внутренних усилий. Примеры использования метода сечений. - Мысленно рассекаем объект по интересующему сечению. - Определяем часть объекта по одну из сторон сечения. - Заменяем действия отброшенной части неизвестными усилиями. - Составляем уравнения равновесия (6 штук: проекции сил и моментов на оси). Закон Гука для одноосного напряжённого состояния в точке и закон Гука для чистого сдвига. Модули упругости первого и второго рода, их физический смысл, математический смысл и графическая интерпретация. Коэффициент Пуассона. Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см2. G – модуль сдвига (модуль упругости II рода). Размерность модуля G такая же, как и у модуля Е, т.е. кГ/см2. μ – коэффициент Пуассона (коэффициент пропорциональности). 8. Центральное растяжение (сжатие) прямого бруса. Определение внутренних продольных сил методом сечений. Правило знаков для внутренних продольных сил. Привести примеры расчёта внутренних продольных сил. Брус испытывает состояние центрального растяжения (сжатия) в том случае, если в его поперечных сечениях возникают центральные продольные силы Nz (т.е. внутренняя сила, линия действия которой направлена по оси z), а остальные 5 силовых факторов равны нулю (Qx=Qy=Mx=My=Mz=0). Правило знаков для Nz: истинная растягивающая сила – «+», истинная сжимающая сила – «-». Опытное изучение механических свойств материалов при растяжении (сжатии). Принцип Сен-Венана. Диаграмма растяжения образца. Разгрузка и повторное нагружение. Наклёп. Основные механические, прочностные и деформационные характеристики материала. Механические свойства материалов вычисляют с помощью испытательных машин, которые бывают рычажными и гидравлическими. В рычажной машине усилие создаётся при помощи груза, действующего на образец через систему рычагов, а в гидравлической – с помощью гидравлического давления. Принцип Сен-Венана: Характер распределения напряжения в поперечных сечениях достаточно удалённых (практически на расстояния, равные характерному поперечному размеру стержня) от места приложения нагрузок, продольных сил не зависит от способа приложения этих сил, если они имеют один и тот же статический эквивалент. Однако в зоне приложения нагрузок закон распределения напряжения может заметно отличаться от закона распределения в достаточно удалённых сечениях. Если испытуемый образец, не доводя до разрушения, разгрузить, то в процессе разгрузки зависимость между силой Р и удлинением Δl образец получит остаточное удлинение. Если образец был нагружен на участке, на котором соблюдается закон Гука, а затем разгружен, то удлинение будет чисто упругим. При повторном нагружении пропадёт промежуточная разгрузка. Наклёп (нагартовка) – явление повышения упругих свойств материала в результате предварительного пластического деформирования. Предел пропорциональности – наибольшее напряжение, до которого материал следует закону Гука. Предел упругости – наибольшее напряжение, до которого материал не получает остаточных деформаций. Предел текучести – напряжение, при котором происходит рост деформации без заметного увеличения нагрузки. Предел прочности – максимальное напряжение, которое может выдержать образец, не разрушаясь. 13. Физический и условный пределы текучести материалов при испытании образцов на растяжение, предел прочности. Допускаемые напряжения при расчёте на прочность центрально растянутого (сжатого) бруса. Нормативный и фактический коэффициенты запаса прочности. Привести числовые примеры. В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация εост=0,002 или 0,2%. В некоторых случаях устанавливается предел εост=0,5%. max|σz|=[σ]. max|σz|растяж≤[σ]растяж; max|σz|сжатия≤[σ]сжатия. Определение внутренних усилий, возникающих в поперечных сечениях стержневых элементов плоской статически определимой рамы, нагруженной системой внешних усилий, действующих в плоскости рамы. Правила знаков для внутренних усилий. - Найти реакции связей, наложенных на раму. - Методом сечений определить внутренние усилия. Если сумма продольных сил, действующих на отсечённую часть рамы, положительная, то ордината силы Nz в сечении откладывается вверх. Если же сумма продольных сил, действующих на отсечённую часть рамы, отрицательная, то ордината силы Nz в сечении откладывается вниз. Если сумма поперечных сил, действующих на отсечённую часть рамы, положительная, то ордината силы Qy в сечении откладывается вверх. Если же равнодействующая поперечная сила слева от сечения даёт отрицательный результат, то ордината силы Qy откладывается вниз. Если сумма моментов сил, действующих на левую часть рамы, даёт равнодействующий момент, направленный по часовой стрелке, то ордината изгибающего момента в сечении откладывается вверх. Если же равнодействующий внешний момент слева от сечения направлен против хода часовой стрелки, то ордината изгибающего момента откладывается вниз. Геометрические характеристики плоских фигур (статический момент площади, осевые моменты инерции, центробежный момент инерции, полярный момент инерции, радиус инерции). Их интегральные выражения. Статические моменты площади относительно центральных и нецентральных осей плоской фигуры. В случае центральных осей: 24. Вывод формул для определения осевых моментов инерции прямоугольника, треугольника, круга, кольца. Прямоугольник: Треугольник: Круг: Кольцо: 25. Преобразование моментов инерции плоской фигуры при параллельном переносе осей координат. В случае центральных осей: 26. Преобразование моментов инерции плоской фигуры при повороте осей координат. Главные моменты инерции. Главные центральные оси плоской фигуры. Моменты инерции плоских симметричных фигур. Для плоских симметричных фигур: Прямой чистый изгиб прямого бруса. Постановка и решение задачи об определении напряжений, возникающих в поперечных сечениях бруса, обладающих, по крайней мере, одной осью симметрии, с которой совпадает силовая линия. Три стороны задачи. Чистым изгибом называется такой изгиб, при котором в поперечных сечениях прямого бруса возникает только изгибающий момент, а остальные факторы (поперечные и продольные силы) равны нулю. Изгиб называется прямым, если силовая линия совпадает с одной из главных центральных осей поперечных сечений балки (главная центральная ось – это главная ось, проходящая через центр сечения). Закон Гука: Плоское напряжённое состояние в точке. Аналитическое исследование нормальных и касательных напряжений, возникающих в произвольно задаваемых площадках, перпендикулярных плоскости действия заданных напряжений. Выделяем из сплошной линейно-упругой среды бесконечно малый объём тремя парами ортогональных площадок (в частности - взаимно перпендикулярных плоскостейыделяем из сплошной линейно-упругой среды бесконечно малый объём тремя парами ортогональных площадок ()Д.И.()вается прямым. ). 39. Исследование частных случаев плоского напряжённого состояния в точке. Привести примеры. Максимальное касательное напряжение (τmax) возникает в площадках, расположенных под углом ±45° к главным площадкам. 40. Графическое исследование плоского напряжённого состояния в точке. Круговая диаграмма напряжений (круг Мора). Привести примеры. Свободное кручение бруса круглого поперечного сечения. Постановка и решение задачи об определении напряжений, возникающих в поперечных сечениях бруса, деформаций и перемещений поперечных сечений бруса. Жёсткость бруса при кручении. Три стороны задачи. Кручение – см. вопрос 49. Основные гипотезы о деформируемом теле. Примеры использования гипотез в расчётах напряжений, деформаций, перемещений. = Гипотеза сплошности и непрерывности материала. Материал сплошной (непрерывный). = Гипотеза однородности свойств материала по всему объёму (макроскопическая гипотеза). = Гипотеза изотропности. Во всех направлениях свойства одинаковы. = Гипотеза естественного состояния материала. Основные принципы, упрощающие расчёт моделей объектов. Примеры применения этих принципов в прочностных расчётах. = Принцип мгновенного отвердевания (принцип неизменности начальных размеров деформированной системы). При определении опорных реакций или каких-либо неизвестных сил из условий равновесия, считается, что под действием приложенных усилий, размеры конструкции не изменяются. = Принцип освобождаемости (от связей, наложенных на систему). Усилия, действующие на конструкцию со стороны других систем через связи в виде опор, учитываются в уравнение равновесия без конструктивных особенностей этих других систем (все системы, действующие на данную систему, заменяются соответствующими усилиями, действующими по месту приложения). = Принцип независимости действия сил. Последовательность приложения (порядок приложения) сил (усилий) к данной конструкции даёт один и тот же результат, как и другой порядок приложения к той же самой системе сил. = Принцип суперпозиции (наложения). Результат действия системы сил на конструкцию равен сумме результатов действий каждого из этих сил на конструкцию. = Принцип Сен-Венана. Для однородного стержня вынужденные силы распределены по сечению равномерно, так как из рассмотрения исключаются особенности конкретно взятого стержня в условиях его закрепления на концах. 3. Классификация сил (нагрузок) и объектов, изучаемых в курсе сопротивления материалов. Размерности нагрузок. Силы: Усилия, приложенные к данному телу, сила распределённой нагрузки, моменты, сила гравитации, сила инерции. Объекты: Тонкий стержень, оболочка, массив, тонкостенный стержень. Основные понятия о деформируемом теле: линейные и угловые перемещения и деформации; упругость, пластичность, хрупкость; изотропия и анизотропия. Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки образует деформированное состояние в точке. Упругость – свойство тела восстанавливать свои первоначальные размеры. Пластичность – способность материала получать большие остаточные деформации. Хрупкость – способность материала разрушаться без образования заметных остаточных перемещений. Изотропность – свойства любого тела, выделенного из сплошной среды не зависят от его исходной ориентации в пределах этой среды. (Изотр.: металлы, анизотр.: дерево, бумага). 5. Метод сечений для определения внутренних усилий. Примеры использования метода сечений. - Мысленно рассекаем объект по интересующему сечению. - Определяем часть объекта по одну из сторон сечения. - Заменяем действия отброшенной части неизвестными усилиями. - Составляем уравнения равновесия (6 штук: проекции сил и моментов на оси). Напряжение в точке. Полное, нормальное, касательное напряжения. Размерности напряжения. Напряжение – мера распределения внутренних сил по сечению. Полное напряжение Нормальное напряжение – проекция вектора полного напряжения на нормаль обозначается через σ. Касательное напряжение – составляющие напряжения в плоскости сечения. Закон Гука для одноосного напряжённого состояния в точке и закон Гука для чистого сдвига. Модули упругости первого и второго рода, их физический смысл, математический смысл и графическая интерпретация. Коэффициент Пуассона. Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см2. G – модуль сдвига (модуль упругости II рода). Размерность модуля G такая же, как и у модуля Е, т.е. кГ/см2. μ – коэффициент Пуассона (коэффициент пропорциональности). 8. Центральное растяжение (сжатие) прямого бруса. Определение внутренних продольных сил методом сечений. Правило знаков для внутренних продольных сил. Привести примеры расчёта внутренних продольных сил. Брус испытывает состояние центрального растяжения (сжатия) в том случае, если в его поперечных сечениях возникают центральные продольные силы Nz (т.е. внутренняя сила, линия действия которой направлена по оси z), а остальные 5 силовых факторов равны нулю (Qx=Qy=Mx=My=Mz=0). Правило знаков для Nz: истинная растягивающая сила – «+», истинная сжимающая сила – «-». infopedia.su Количество просмотров публикации Размерность напряжений. - 83 Напряжения измеряются в МПа. 1МПа= Па= Н/м²= Н/мм² 1МПа=1Н/мм² Очевидно, что реальные (расчетные) напряжения в конструкции не могут расти до бесконечности, они должны быть ограничены. Коэффициент запаса прочности - это отношение некоторого предельного напряжения к максимальному напряжению, возникаемому в конструкции. Максимальное напряжение в конструкции не должно превышать допускаемого напряжения для данного материала определенного с учетом коэффициента запаса для заданных условий работы. Коэффициент запаса - число большее единицы. Размерность напряжений. - понятие и виды. Классификация и особенности категории "Размерность напряжений." 2014, 2015. referatwork.ru Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции. Выделим на плоскости сечения площадку A; по этой площадке будет действовать внутренняя сила R. Величина отношения R/A=pсрназывается средним напряжением на площадке A. Истинное напряжение в точке А получим устремив A к нулю: Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения. Очевидно, что . Касательное напряжение в свою очередь может быть разложено по направлениям осейx и y (τzх, τzу). Размерность напряжений – Н/м2 (Па). При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела. Касат. напряжение на 2-ух взаимно перпендик. площ. направлены к ребру или от ребра и равны по величине Деформац – наз. взаимное перемещение точек или сечений тела по сравн с полож-ями тела которые они занимали до приложения внеш сил бывают: упругие и пластические а) линейная деформация мерой явл относительное удлинение эпсила =l1-l/l б) поперечная деф мерой явл. относительное сужение эпсила штрих=|b1-b|/b Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. . Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: , — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя. Он установил связь между напряжением, растяжением и продольной деформацией.где Е – коэффициент пропорциональности (модуль упругости материала). Модуль упругости характеризует жёсткость материала, т.е. способность сопротивляться деформациям. (чем больше Е, тем менее растяжимый материал) Потенциальная энергия деформации: Внешние силы, приложенные к упругому телу, совершают работу. Обозначим её через А. В результате этой работы накапливается потенциальная энергия деформированного тела U. Кроме того, работа идёт на сообщение скорости массе тела, т.е. преобразуется в кинетическую энергию К. Баланс энергии имеет вид А = U + К. studfiles.net Е = F/ Qo. В общем случае напряженность поля Е = F/Q. Т.е. напряженность в данной точке пространства есть отношение силы, действующей на заряд, помещенный в эту точку к величине этого заряда. Единица измерения напряженности электростатического поля — 1 Н/Кл =1В/м. Напряженность 1Н/Кл - это напряженность такого поля, которое на точечный заряд 1 Кл действует силой 1 Н, эту единицу в системе СИ называют В/м. Если поле создается положительным зарядом, то вектор напряженности такого поля направлен от заряда вдоль радиуса-вектора, если поле создается отрицательным зарядом, то вектор напряженности поля Е направлен к заряду. Е = - gradj. Вектор напряженности электрического поля направлен в сторону убывания потенциала. В вакууме напряженность электрического поля удовлетворяет принципу суперпозиции, согласно которому полная напряженность поля в точке равна геометрической сумме напряженностей полей, создаваемых отдельными заряженными частицами. megabook.ru14.Понятие о напряжениях. Нормальные и касательные напряжения. Размерность напряжение
Напряжение в точке. Полное, нормальное, касательное напряжения. Размерности напряжения.
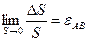 - линейная деформация (или просто деформация) в точке А по направлению АВ.
- линейная деформация (или просто деформация) в точке А по направлению АВ. - Среднее удлинение отрезка АВ.
- Среднее удлинение отрезка АВ.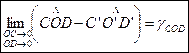 - угловая деформация (или угол сдвига) в точке О в плоскости COD.
- угловая деформация (или угол сдвига) в точке О в плоскости COD. - закон Гука для одноосного напряжённого состояния в точке.
- закон Гука для одноосного напряжённого состояния в точке. - закон Гука для сдвига.
- закон Гука для сдвига. .
. . Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).
. Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала). , n>1(!) – нормативный коэффициент запаса прочности.
, n>1(!) – нормативный коэффициент запаса прочности.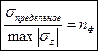 - фактический коэффициент запаса прочности. n>1(!).
- фактический коэффициент запаса прочности. n>1(!).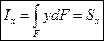 - статический момент площади фигуры относительно оси х.
- статический момент площади фигуры относительно оси х. - статический момент площади фигуры относительно оси у.
- статический момент площади фигуры относительно оси у. - осевой момент инерции относительно оси х.
- осевой момент инерции относительно оси х. - осевой момент инерции относительно оси у.
- осевой момент инерции относительно оси у. - центробежный момент инерции площади плоской фигуры относительно осей х, у.
- центробежный момент инерции площади плоской фигуры относительно осей х, у. - полярный момент инерции сечения.
- полярный момент инерции сечения.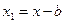 ,
, 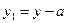 .
. - статический момент площади относительно нецентральной оси х1 плоской фигуры.
- статический момент площади относительно нецентральной оси х1 плоской фигуры. - статический момент площади относительно нецентральной оси у1 плоской фигуры.
- статический момент площади относительно нецентральной оси у1 плоской фигуры.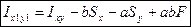 - центробежный момент инерции площади плоской фигуры относительно осей х1 и у1.
- центробежный момент инерции площади плоской фигуры относительно осей х1 и у1.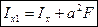 ,
,  ,
, 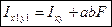 .
.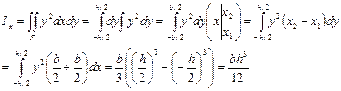
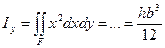 ,
, 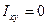

 ,
, 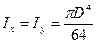 ,
,  ,
, .
.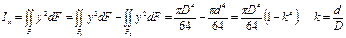 .
. - статический момент площади относительно нецентральной оси х1 плоской фигуры.
- статический момент площади относительно нецентральной оси х1 плоской фигуры. - статический момент площади относительно нецентральной оси у1 плоской фигуры.
- статический момент площади относительно нецентральной оси у1 плоской фигуры.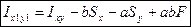 - центробежный момент инерции площади плоской фигуры относительно осей х1 и у1.
- центробежный момент инерции площади плоской фигуры относительно осей х1 и у1.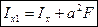 ,
,  ,
, 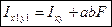 .
.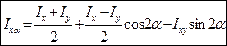


 - главные моменты инерции, а оси, относительно которых они достигаются, называются главными осями (среди всех осей, проходящих через фиксируемую точку плоскости).
- главные моменты инерции, а оси, относительно которых они достигаются, называются главными осями (среди всех осей, проходящих через фиксируемую точку плоскости).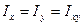
 ,
, ,
, 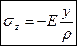 ,
, 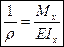 - кривизна балки равна отношению внутреннего изгибающего момента к жёсткости балки (внутренний изгибающий момент равен отношению жесткости балки к радиусу инерции).
- кривизна балки равна отношению внутреннего изгибающего момента к жёсткости балки (внутренний изгибающий момент равен отношению жесткости балки к радиусу инерции).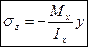 . Закон распределения напряжения по силовой линии – линейный.
. Закон распределения напряжения по силовой линии – линейный.

 ,
, 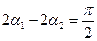 ,
, 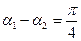 .
. ,
, 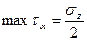 .
.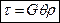 - закон Гука для сдвига, θ – относительный угол закручивания, ρ – радиус.
- закон Гука для сдвига, θ – относительный угол закручивания, ρ – радиус. - жёсткость бруса при кручении.
- жёсткость бруса при кручении. - относительный угол закручивания.
- относительный угол закручивания. - угол взаимного поворота сечений.
- угол взаимного поворота сечений. - касательные напряжения.
- касательные напряжения.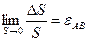 - линейная деформация (или просто деформация) в точке А по направлению АВ.
- линейная деформация (или просто деформация) в точке А по направлению АВ. - Среднее удлинение отрезка АВ.
- Среднее удлинение отрезка АВ.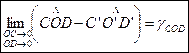 - угловая деформация (или угол сдвига) в точке О в плоскости COD.
- угловая деформация (или угол сдвига) в точке О в плоскости COD.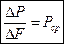 , где
, где  - внутренняя сила, выявленная на площадке
- внутренняя сила, выявленная на площадке  .
.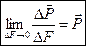 .
. , где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается.
, где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается. , где
, где  (для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.
(для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига. - закон Гука для одноосного напряжённого состояния в точке.
- закон Гука для одноосного напряжённого состояния в точке. - закон Гука для сдвига.
- закон Гука для сдвига. .
. . Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).
. Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).Размерность напряжений.
Образование
 Размерность напряжений.
Размерность напряжений. Наименование параметра Значение Тема статьи: Размерность напряжений. Рубрика (тематическая категория) Образование Условия прочности конструкций и их элементов
В сопротивлении материалов основным критерием надежности конструкции является ее прочность.
Условия прочности в общем виде
Прочными называют конструкции и составляющие их элементы, в которых максимальныенапряжения не превышают допустимых значений. рмах≤[р]
Здесь рmax – максимальные значения полного напряжения в элементах конструкции, [p] – величина допустимых значений напряжений для материала элементов.
К сожалению, довольно часто, задача рассчитать величину полных напряжений p является сложновыполнимой, в связи с этим для оценки прочности используют значения нормальных σ и касательных τ напряжений, которые определяются сравнительно просто.
σмах≤[σ] τ мах≤[ τ], где σmax и τmax – максимальные нормальные и касательные напряжения соответственно, [σ] и [τ] – допустимые нормальные и касательные напряжения для материала элемента.
14.Понятие о напряжениях. Нормальные и касательные напряжения
16.Закон парности касательных напряжений
17.Понятие о деформациях. Мера линейной, поперечной и угловой деформации
18.Гипотеза плоских сечений
19.Закон Гука (1670). Физический смысл входящих в него величин
Напряженность электрического поля — Мегаэнциклопедия Кирилла и Мефодия — статья
Напряженность электри́ческого по́ля (Е) — основная силовая характеристика электрического поля, определяемая силой (F), действующей на точечный (единичный) положительный электрический заряд (Qo), помещенный в данную точку поля. Заряд должен быть малым, чтобы не изменять ни величины, ни расположения тех зарядов, которые порождают исследуемое поле (т. е. заряд, не искажающий поля, которое с его помощью изучается, при этом собственным электрическим полем точечного заряда пренебрегают).
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''








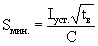


Поделиться с друзьями: