В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом. Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель. Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений. Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы. К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении. В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула: R(общ)=1/(1/R1+1/R2+1/R3+1/Rn). причем : Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу: R(общ)=R1*R2/R1+R2. причем: Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов: R(общ)=R1\n. причем : Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь. Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее: R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом. Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%. Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой. Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт. Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом. Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры. Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи. elektro.guru Условно, потому что во многом эта характеристика зависит от внешних условий, например температуры. Сопротивление же какого-либо конкретного элемента (мы будем говорить о резисторах) складывается из многих факторов, например, из геометрических параметров, а когда речь идет о цепи переменного тока, то в расчеты включают также индуктивное и емкостное сопротивление, но об этом мы расскажем позже. Пока же — немного теории. В 1826 году немецкий физик Георг Ом на основе своих опытов вывел закон, согласно которому сила тока на участке цепи прямо пропорциональна напряжению, которое к нему приложено, и обратно пропорциональна сопротивлению участка. Из школьного курса мы знаем этот закон: I=U/R Позже он был сформулирован и для полной цепи: I=ε/(R+r) Где ε — ЭДС источника, R — сопротивление цепи, а r — сопротивление источника. Электрический заряд при своем перемещении совершает работу. Может быть, это незаметно глазу, но вот пощупать результат этой работы можно: электроприборы у нас греются, а иногда нагрев — это цель, а не побочное явление. Не верите — ну, электроплитки, ТЭНы, утюги как раз это свойство и эксплуатируют. Правда, руками это проверять не советую. Мощностью у нас называют работу, совершенную за единицу времени. Попробуем вычислить мощность электроприбора, включенного в цепь. Поскольку он обладает сопротивлением, обозначим его R, работу — А, мощность — Р, заряд — Q, а время — Δt. Итак, заряд проходит по цепи под действием напряжения U, которое совершает работу по его перемещению на участке цепи за время Δt: Р=А/Δt , А=UQ Произведем подстановку: Р=UQ/Δt Ну а поскольку Q/Δt — не что иное, как сила тока I, получаем: Р=UI Свяжем полученное выражение с законом Ома и получим: Р=I^2*R, P=U^2/R В реальной жизни мы редко имеем дело с одним проводником и одним источником. Достаточно взглянуть в любую принципиальную электрическую схему, например, такую простенькую: (это схема микроволновки «Электроника») можно увидеть, что элементы в схеме соединены по-разному, но мы покажем вам базовые закономерности, которые работают в цепях. Если взять замкнутую электрическую цепь, по которой течет заряд, то можно определенно сказать: он никуда не денется. Сумма всех зарядов, которые текут в одной цепи, всегда одинакова. Это называется законом сохранения заряда, частным случаем общего закона сохранения (как говорится, если в одном месте что-то убудет, в другом непременно прибудет). Отсюда мы и выводим тот факт, что в каждом узле цепи сумма токов равна нулю. То есть, если ток «приходит» в точку по ветке и «уходит» по двум — значит, первый равен сумме второго и третьего. На этой картинке мы видим, что I1+I4=I2+I3 Это называется первым правилом Кирхгофа. Если наша цепь не будет содержать узлов, значит, ток в ней будет величиной постоянной, а элементы, один за другим поставленные в цепь, будут давать падение напряжения. При этом общее напряжение в цепи останется тем же. Отсюда вытекает второе правило Кирхгофа: сумма напряжений на участках цепи будет равна ЭДС источников тока, входящий в эту цепь. Если у нас источник один, то будет верно равенство: ε=U1+U2+U3+…+Un Сумма падений напряжения будет, таким образом, нулевой. В ситуациях, когда мы имеем дело с переменным током, падение будет наблюдаться на участках с конденсаторами и катушками — в цепях переменного тока у них появляется сопротивление (об этом позже). Теперь, когда мы познакомились с теоретической частью, можем перейти к более приближенному к суровой реальности вопросу, а именно — расчету последовательного и параллельного соединения резисторов. Рассчитаем параметры цепей с разным типом соединения. Последовательное соединение. Как мы видим из рисунка, резисторы соединены один за другим, последовательным способом. Значит, ток в этой цепи — величина постоянная, а напряжение, исходя из второго правила Кирхгофа — U=U1+U2+U3 /напряжение при последовательном соединении/ Поскольку из закона Ома получается U=IR, то IR=IR1+IR2+IR3, следовательно, сопротивление всей цепи R=R1+R2+R3 /сопротивление при последовательном соединении/ а ее потребляемая мощность Р=I^2*R Параллельное соединение. I=I1+I2+I3 /сила тока при параллельном соединении/ Выражаем ток через напряжение и сопротивление, и получим: U/R=U/R1+U/R2+U/R3 1/R=1/R1+1/R2+1/R3 R=1/(1/R1+1/R2+1/R3) /сопротивление при параллельном соединении/ Ну а мощность будет выражаться так: P=U^2/R Исходя из вышеперечисленных закономерностей, вы сможете рассчитывать самые причудливые соединения резисторов, можете попрактиковаться, взяв в библиотеке задачник. Как уже было сказано ранее, элемент, который ставится в цепь для нагрузки, называется резистором. Ставят его для разных целей, главным образом для того, чтобы изменить тот или иной параметр на участке цепи. Например, понизить напряжение или силу тока, чтобы деталь, стоящая за резистором, не сгорела. Предприятиями выпускается большой ассортимент таких изделий, и их можно по-разному классифицировать. Номинально резистор имеет то сопротивление, которое указано на нем, а по факту оно может зависеть от напряжения в сети (нелинейность), иметь разброс параметра (иногда до 20% доходит). По применяемой технологии резисторы можно разделить на: Помимо этого, большое распространение получили переменные резисторы, значение сопротивления которых можно регулировать. Делается это чаще всего отверткой. Необходимость в таких изделиях продиктована разбросом параметров у обычных резисторов, а подстроечный вариант позволяет регулировать сопротивление. Все вышесказанное актуально для цепей постоянного тока и переменного при невысоких частотах, и все это — при нормальных условиях внешней среды. Расчеты цепей при нарушении этих условий нуждаются в дополнительной корректировке: это связано с ограниченностью действия закона Ома. С чем связаны ограничения? Вот несколько примеров: Все это прекрасно работает. Не верите — можете поэкспериментировать у себя дома или провести замеры тестером. Например, изучить елочную гирлянду или показания счетчиков при включенных электроприборах (напомню, что в гирлянде лампочки соединены последовательно, а розетки в доме — параллельно). Удачи! instrument.guru Виды соединения резисторов: 1) Последовательное соединение резисторов: Если: При последовательном соединении общее сопротивление резисторов будет больше чем наибольшее из сопротивлений. 2) Параллельное соединение резисторов: При параллельном соединении суммируются величины, которые обратно пропорциональны сопротивлению: Если цепь можно разделить на составляющие подблоки, параллельно или последовательно включенные между собой, то сначала высчитывается сопротивление на каждом подблоке, затем заменяют каждый подблок его эквивалентным сопротивлением, и таким путем находится общее сопротивление на цепи. 3) Смешанное соединение резисторов: Схема состоит из двух параллельно включенных блоков, один из которых состоит из последовательно включенных резисторов R1 и R2, общее сопротивление которых равно R1+R2, другой из резистора R3, общая проводимость равняется: то есть общее сопротивление будет равно: Для расчета таких цепей, которые нельзя разделить на отдельные блоки параллельно или последовательно соединенные между собой, применяют правило Кирхгофа. Также иногда используют преобразование треугольник-звезда, затем применяя принцип симметрии. 4) Делитель напряжения. Если R=9R1, то UWY=0,1UWE, то есть входное напряжение поделиться в десять раз. 44kw.com Как подключить резистор? Резистор – это элемент электрической цепи, главным свойством которого является определенное активное сопротивление. Существует масса разновидностей резисторов – постоянные, переменные, варисторы, терморезисторы и т.п., а также масса возможных схем включения. В этой статье рассмотрим основные схемы включения и разберем, как подключить резистор. Последовательно соединение – одна из основных схем включения резистора. Допустим, нам необходимо спаять два резистора в последовательное соединение. В таком случае: Если необходимо соединить больше резисторов, действуйте аналогично (см. рисунок). Помните, при последовательном соединении общее сопротивление схемы будет равняться сумме сопротивлений, включенных в нее резисторов. Параллельное соединение – также одна из основных схем включения резисторов. Для параллельного соединения двух резисторов: elhow.ru С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь. Резистор — пассивный элемент, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов: Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников: Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли. Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором. Примером последовательного соединения проводников в быту является ёлочная гирлянда. При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном. Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников. В таких схемах значение напряжения постоянно. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения. Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника. Примеры параллельного соединения проводников: Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора. Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты. Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты. В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение. instrument.guru Смешанным соединением называют сочетание последовательного и параллельного соединений резисторов. Большое разнообразие этих соединений не позволяет вывести общую формулу для определения эквивалентного сопротивления цепи. Поэтому в каждом конкретном случае, используя методы расчета при последовательном и параллельном соединениях, можно рассчитать эквивалентное сопротивление при смешанном соединении. Поясним это на конкретном примере расчета электрической цепи (рис. 1.20 а). Электрическую цепь постепенно упрощают и приводят к простейшему виду (рис. 1.20 б, в) Проверка: 1) 1.8.4. Метод преобразований треугольника резисторов в эквивалентную звезду и наоборот Рассмотрим две электрические цепи (рис. 1.21). Одна из них имеет вид треугольника, другая – трехлучевой звезды. В дальнейшем такие соединения будем называть соответственно соединением в треугольник и соединением звездой. Рис. 1.21 Соединения такого вида очень распространены в трехфазных цепях, в которых часто возникает необходимость перехода от одного вида соединения к другому (эквивалентному). Эквивалентность треугольника и звезды резисторов заключается в том, что их замена не изменяет потенциалов узловых точек (φа, φbи φс), являющихся вершинами треугольника и эквивалентной звезды. Не изменяются также токи, напряжения и мощности в остальной части схемы, не затронутой преобразованием. Формулы пересчета без вывода сопротивлений ветвей треугольника При переходе от звезды к треугольнику можно воспользоваться следующими формулами Если сопротивления всех ветвей цепи по схеме треугольник одинаковы, т.е. 1.8.5. Последовательное соединение источников энергии В практике последовательное и согласное включение источников применяют для увеличения напряжения. Рассмотрим схему с двумя согласно и одним встречно включенными источниками (рис. 1.22). Рис. 1.22 По второму закону Кирхгофа запишем Отсюда где Напряжения на зажимах источников и приемника При последовательном соединении Онлайн калькулятор для параллельного соединения резисторов. Соединения резисторов схемы
Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета
Параллельное соединение: общая информация
Расчет сопротивления
Универсальная схема расчета
Пример расчета
Важные нюансы
Заключение
закон Ома, формулы и схемы, примеры расчета
 Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.
Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.Закон Ома
Мощность прибора
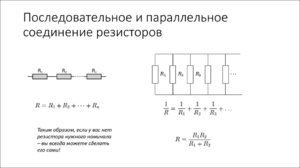
Последовательное и параллельное соединение
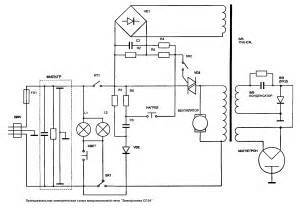
Правила Кирхгофа
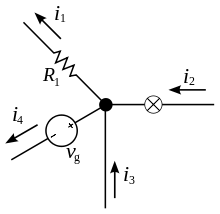
Примеры расчетов
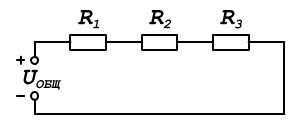
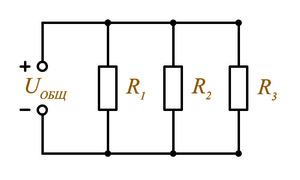 На этой картинке мы видим, что резисторы соединены параллельно друг другу. Произведем расчет параллельного соединения резисторов. Напряжение при параллельном соединении постоянно, а вот ток во всей цепи, исходя из первого правила Кирхгофа, складывается из тока по каждой ветке отдельно:
На этой картинке мы видим, что резисторы соединены параллельно друг другу. Произведем расчет параллельного соединения резисторов. Напряжение при параллельном соединении постоянно, а вот ток во всей цепи, исходя из первого правила Кирхгофа, складывается из тока по каждой ветке отдельно:Типы резисторов
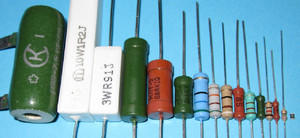 Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током. Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.
Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током. Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.Соединения резисторов / Школа электрика / Коллективный блог
 Резистор – пассивный элемент электроцепи, в идеале характеризуемый только сопротивляемостью электрическому току, то есть для идеального резистора в любом временном промежутке будет выполняться закон Ома для участка цепи: на резисторе мгновенное значение напряжения прямо пропорционально электрическому току, проходящему через него. На практике же резисторы в той или иной мере обладают паразитной индуктивностью и паразитной емкостью.
Резистор – пассивный элемент электроцепи, в идеале характеризуемый только сопротивляемостью электрическому току, то есть для идеального резистора в любом временном промежутке будет выполняться закон Ома для участка цепи: на резисторе мгновенное значение напряжения прямо пропорционально электрическому току, проходящему через него. На практике же резисторы в той или иной мере обладают паразитной индуктивностью и паразитной емкостью. При таком соединении резисторов их сопротивление суммируется:
При таком соединении резисторов их сопротивление суммируется: 
 То общее сопротивление будет равно:
То общее сопротивление будет равно:







ВложениеРазмер 1.png 657 байтов 2.png 634 байта 3.png 440 байтов 4.png 546 байтов 5.png 794 байта 6.png 809 байтов 7.png 542 байта 8.png 871 байт 9.png 1 КБ 10.png 2.64 КБ 11.png 1.02 КБ 12.jpg 18.1 КБ Как подключить резистор?
Последовательное соединение
Параллельное соединение
Схемы с параллельным соединением резисторов, варианты расчётов: ручной, онлайн-калькулятор
 Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.Виды соединений
Последовательное соединение проводников
 В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно. Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно. Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.Параллельное соединение резисторов
Смешанное соединение проводников
 Этот вид соединения состоит из каскадов резисторов. Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Этот вид соединения состоит из каскадов резисторов. Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.Смешанное соединение резисторов
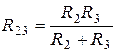 ;
; 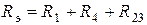 ;
; 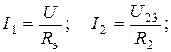
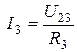 ;
;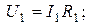
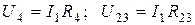 .
. 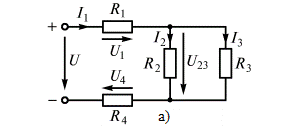
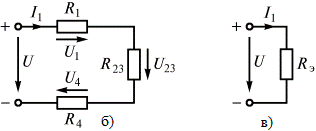 Рис. 1.20
Рис. 1.20
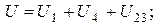 2)
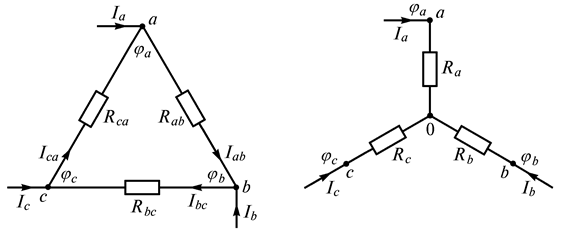
2) 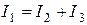 .
.
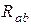 ,
, 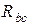 ,
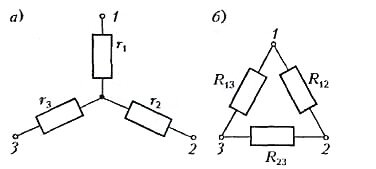
, 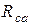 в эквивалентную звезду
в эквивалентную звезду  ,
, 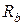 ,
, 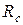 имеют вид
имеют вид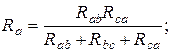
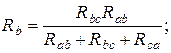
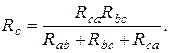 (1.39)
(1.39)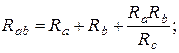
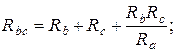
 (1.40)
(1.40)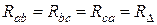 , сопротивления эквивалентной звезды будут также одинаковые:
, сопротивления эквивалентной звезды будут также одинаковые: 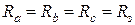 , причем
, причем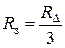 .
.
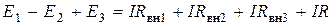 . (1.41)
. (1.41)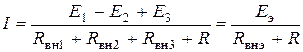 , (1.42)
, (1.42)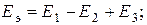
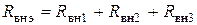 .
.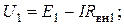
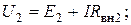
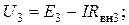
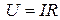 .
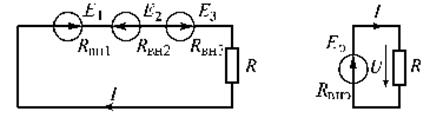
. источников с одинаковыми параметрами
источников с одинаковыми параметрами . (1.43)
. (1.43)Похожие статьи:
poznayka.org





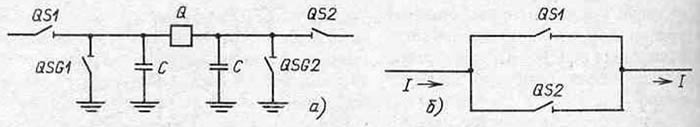






Поделиться с друзьями: