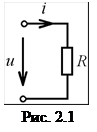
Задания Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. Определить токи во всех ветвях схемы методом контурных токов. Определить токи во всех ветвях схемы методом узловых потенциалов. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой. Составить баланс мощностей в исходной схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Определить ток в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе. Начертить потенциальную диаграмму для любого замкнутого контура, включая обе э.д.с. R1=18Ом; R2=40Ом; R3=32Ом; R4=80Ом; R5=60Ом; R6=44Ом; E2=60В; E3=28В; Линейные цепи постоянного тока. 1.Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. Направим произвольно токи в ветвях схемы. В схеме четыре узла значит по первому закону Кирхгофа составим три уравнения. Составим уравнения узлов а,b,с. Для узла а -I3+I5-I6=0 Для узла b -I1-I2+I6=0 Для узла c I1+I3-I4=0 По второму закону Кирхгофа составим 3 уравнения. Так как общее число уравнений 6, то число неизвестных тоже 6. Примем направление обхода контуров против часовой стрелки. Для контура I; -R2I2-R5I5- R6I6 =E2 Для контура II; R3I3+R4I4+R5I5=E3 Для контура III; -R1I1+R2I2-R4I4=-E2 2. Определить токи во всех ветвях методом контурных токов. Выберем направления обхода контуров против часовой стрелки. Найдем сопротивления контуров R11=R2+R5+R6=40+60+44=144Ом R22=R3+R4+R5=32+80+60=172Ом R33=R1+R2+R4=18+40+80=138Ом Смежные сопротивления: R12=R21=-R5=-60Ом R13=R31=-R2=-40Ом R23=R32=-R4=-80Ом E11=E2=60В E22=E3=28В E33=-E2=-60В Записываем систему уравнений. R11I11+R12I22+R13I33=E11 R21I11+R22I22+R23I33=E22 R31I11+R32I22+R33I33=E33 144I11-60I22-40I33=60 -60I11+172I22-80I33=28 -40I11-80I22+138I33=-60 Составляем определитель: 144 -60 -40 = -60 172 -80 =1340000 -40 -80 138 60 -60 -40 1= 28 172 -80 =660800 -60 -80 138 144 60 -40 2= -60 28 -80 =365200 -40 -28 138 144 -60 60 3= -60 172 28 =-179500 -40 -80 -60 I11=1/= 0,493A; I1=- I33= 0,134A; I4=I22-I33= 0,406A I22=2/= 0,272A; I2=I33-I11= -0,627A; I5=I22-I11= -0,221A I33=3/= -0,134A; I3=I22= 0,272 A; I6=-I11= -0,493A Знаки « - » перед значениями токов указывают, что токи направлены в противоположную сторону от выбранных нами направлений. 3. Определить ток в схеме методом узловых потенциалов. Заземлим точку c, приняв её потенциал равным 0. Запишем общую систему уравнений. φ11G11+φ22G12+φ33G13=I11 φ11G21+φ22G22+φ33G32=I22 φ11G31+φ22G32+φ33G31=I33 Узловые проводимости: G11=1/R3+1/R5+1/R6 G22=1/R2+1/R4+1/R5 G33=1/R1+1/R2+1/R6 Смежные проводимости: G12=G21=-1/R5 G13=G31=-1/R6 G23=G32=-1/R2 Узловые токи: I11=-E3/R3; I22=-E2/R2; I33=E2/R2 Подсчитываем проводимости и токи, и подставляя их в общую систему уравнений решаем её. Находим узловые потенциалы. 0,071φ11-0,017φ22-0,023φ33=-0,857 -0,017φ11+0,054φ22-0,025φ33=-1,5 -0,023φ11-0,025φ22+0,103φ33=1,5 0,071 -0,017 -0,023 = -0,017 0,054 -0,025 = 0,0002726 -0,023 -0,025 0,103 -0.857 -0,017 -0,023 1= -1,5 0,054 -0,025 = -0,00522 1,5 -0,025 0,103 0,071 -0,857 -0,023 2 = -0,017 -1,5 -0,025 = -0,00892 -0,023 1,5 0,103 0,071 -0,017 -0,857 3 = -0,017 0,054 -1,5 = 0,0006399 -0,023 -0,025 1,5 Получили значения потенциалов φ11= -19,144 В φ22= -32,718 В φ33= 2,347 В Токи в ветвях схемы вычисляем по закону Ома. Причем не будем менять направления на противоположные для наглядности, что получили те же токи. Т.к. не меняли направления токов то они как и во 2-ом пункте получились отрицательные. 4.Свести результаты расчета токов в таблицу и определить относительную и абсолютную погрешности. Метод контурных токов Метод узловых потенциалов ε,% ∆I,А I1=0,134А I1= 0,13А 0,03 0,004 I2= -0,627А I2= -0,623А 0,006 -0,004 I3= 0,272А I3= 0,227А 0,018 -0,005 I4= 0,406А I4= 0,409А 0,007 -0,003 I5= -0,221А I5= -0,226А 0,023 0,005 I6= -0,493А I6= -0,488А 0,01 -0,005 ε иI рассчитаны по формулам: ε=|(IК-Iφ)/IК|*100%,где IК-ток по МКТ. Iφ-ток по МУП. I=IК-Iφ. 5.Составить баланс мощностей в исходной схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Уравнение баланса: I2кRк=EКIК. Как видим баланс мощностей сходится. Определить ток I1 в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе. Для нахождения тока I1,преобразуем исходную схему, используя теорему об активном двухполюснике. И рассчитаем I1 по формуле: I1=εэкв / Rвх+R1 Для нахождения εэкв исключим из исходной схемы ветвь содержащую ток I1.Произвольно направим токи в полученной схеме. Потенциал узла c примем равным нулю. Для нахождения токов в преобразованной схеме воспользуемся методом двух узлов. Полученные значения токов подставим в выражения для потенциалов. И получим εэкв: εэкв = Найдем Rвх для чего исключим из схемы все источники ЭДС и найдем сопротивление схемы относительно зажимов (bc ). Для нахождения входного сопротивления преобразуем треугольник R4,R5,R6 в звезду R45,R53,R34. Теперь мы можем найти I1. Выберем направление обхода контура fabkdcf. При этом не будем менять направления токов. А значения токов возьмем из второго задания с теми же знаками. Заземлим узел f. φf = 0В Рассчитаем потенциалы остальных точек контура. φa = φf + R3I3= 8,7В φb = φa –I6R6 = 30,4В φk = φb – R2I2 = 55,5В φd = φk - Е2 = -4,5В φc = φd + R4I4 =28В φf = φk – E3 = 0В По полученным данным строим потенциальную диаграмму: studfiles.net По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности. а) Определяем частные токи от ЭДС Е1 при отсутствии ЭДС Е2, т. е. рассчитываем цепь по Показываем направление частных токов от ЭДС E1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания" Ток источника Определяем частные токи от ЭДС Е2 при отсутствии ЭДС Е1 Ток источника Вычисляем токи ветвей исходной цепи выполняя алгебраическое сложение частных токов, учитывая их направление: Источники Е1 и Е2 вырабатывают электрическую энергию, т. к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так: Подставляем числовые значения и вычисляем С учетом погрешности расчетов баланс мощностей получился. Ток ветви I1 A I2 A I3 A I4 A I5 A I6 A Метод расчета Метод контурных токов 0,429 0,081 0,510 0,291 0,219 0,138 Метод наложения 0,429 0,081 0,509 0,189 0,05 0,239 Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви: Возьмем контур АВCА. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А. Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат -потенциалы точек с учетом их знака. Построить входную вольтамперную характеристику схемы нелинейной электрической цепи постоянного тока. Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики. R3=45 Ом; U=140В. ВАХ нэ1-б нэ2-в. ВАХ линейного элемента строим по уравнению. Она представляет собой прямую, проходящую через начало координат. Для определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, UR = 90 В, тогда соответствующее значение тока Соединив полученную точку с началом координат, получим ВАХ линейного элемента. Далее строится общая ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически "сворачиваем" цепь. Начинаем с разветвленного участка. Нелинейные элемент нэ2 и линейный R1 соединены параллельно, их ВАХ I1=f(U1) и I2=f(U2). С учетом этого строим общую для них ВАХ. Для этого задаемся напряжением и складываем токи при этом напряжении I3=I1+I2. Точка пересечения этих значений тока и напряжения дает одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ I3=f(U12). Далее мы имеем характеристики нелинейного элемента I3=f(U3) и нелинейного элемента (нэ12) I3=f(U12), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I3=f(U). Дальнейший расчет цепи производим по полученным графикам. Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значение напряжения, равное 140 В (точка "а"). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ I3=f(U), получим точку "в". Из точки "в" опускаем перпендикуляр на ось тока (точка "с"). Отрезок "ос" дает нам искомое значение общего тока I3=0,9 А. Когда опускаем перпендикуляр из точки "в" на ось тока, то пересекаем ВАХ I3=f(U3) и I3=f(U12) в точках "f' и "d" соответственно. Опуская перпендикуляры из этих точек на ось напряжения, получим напряжения на каждом участке цепи: U3=110В и U12=30 В, но U12=U1=U2, т. к. нелинейные элементы соединены параллельно. Чтобы найти токи I1 и I2 при U12=81 В, опустим перпендикуляр из на ось напряжений до пересечения с ВАХ I1=f(U1) и I2=f(U2) в точках "N" и "М". Опустив из этих точек перпендикуляры на ось токов, получим I2 = 0,5 А и I1 = 0,4 А. В результате имеем следующие значения токов и напряжений на всех элементах цепи: I1=0,4 А; I2 =0,5 А; I3 = 0,9 A; U1=30 В; U2=30 В; U3=110 В. studfiles.net Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров. Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений. При расчете рекомендуется придерживаться следующей последовательности: – выделить все независимые контуры – указать направления обхода контуров (желательно одно и то же для всех контуров) – указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода) – для всех независимых контуров составить уравнения второго закона Кирхгофа – решить полученную систему уравнений любым известным методом – по вычисленным значениям контурных токов определить величины токов в ветвях и их направления. Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E1R3R1E1и R3E2R2R3. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R3, которая принадлежит двум контурам сразу, протекают два контурных тока IK1и IK2, но в противоположных направлениях. E1 = IK1 (R1 + R3) – IK2R3 – E2= –IK1R3+IK2(R2+R3) Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление. Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: IK1=7 A, IK2= – 5 A. Тогда I1= IK1= 7 = 7 A и протекает в резисторе R1так же, как контурный ток IK1по схеме сверху вниз. Ток I2= – IK2= – 5 А и протекает в резисторе R2по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R3 , цепи представленной на рис. 1.10, протекают контурный ток IK1= 7 А по схеме сверху вниз и контурный ток I2= – 5 А по схеме снизу вверх. IK1> IK2и I3= IK1– IK2= 7 – (–5) = 12 А. Ток I3имеет такое же направление, что и ток IK1 , т.е. по схеме сверху вниз. Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений. По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента. Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в) Например, в цепи представленной на рис. 1.11а приемники R3и R4соединены последовательно и их можно заменить одним эквивалентным с сопротивлением R34= R3+ R4. После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R2 и эквивалентный приемник R34включены параллельно. Параллельный участок R2– R34также можно заменить одним эквивалентным с сопротивлением после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно. Входное сопротивление этой цепи R1234= R1+ R234 позволяет найти ток I1исходной цепи рис. 1.11а, пользуясь законом Ома . Напряжение на участке R234легко найти по закону Ома для пассивного участка цепи U234= I1R234. Токи в ветвях R2и R34также находятся по закону Ома . Токи I3= I4, т.к. приемники R3и R4включены последовательно, они равны току I34. studfiles.net Министерство образования и науки Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Алтайский государственный технический университет им. И.И. Ползунова» Факультет информационных технологий Кафедра информационных технологий Отчет защищен с оценкой. Преподаватель Е.М. Патрушев (подпись) (и.о. фамилия) «»2011 г. Отчет по лабораторной работе № 2 «Разветвленные линейные электрические цепи постоянного тока» по дисциплине «Общая электротехника» ЛР 200106.02.000 О. Студент группы ИИТ-01 С. С. Николаенко Преподаватель доцент., к.т.н. Е.М. Патрушев должность, ученая степень и.о., фамилия БАРНАУЛ 2011 Задание: Для электрической схемы, выбираемой по вариантам, выполнить следующее: Упростить схему, заменив источники тока источниками ЭДС . Для полученной схемы выполнить следующее: Составить на основании законов Кирхгофа систему уравнений для расчёта токов во всех ветвях схемы. Определить токи во всех ветвях схемы методом контурных токов. Определить токи во всех ветвях схемы методом узловых потенциалов. Результаты расчёта токов, проведённого двумя методами, свести в таблицу и сравнить между собой. Найти токи для ветвей исходной схемы, в которых было выполнена замена источников тока источниками ЭДС Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Определить ток I1 в заданной по условию схеме с источником тока, используя теорему об активном двухполюснике (эквивалентном генераторе). Программное обеспечение: ОС Windows, система схемотехнического моделирования MicroCap, система для математических расчетов MathCad. Порядок выполнения задания: В системе MicroCap выполнить построение исходной схемы. Определить все токи, узловые напряжения, мощности. Выполнить упрощение исходной схемы, заменив источники тока источниками ЭДС. Для полученной схемы составить матрицы для решения использованием законов Кирхгофа, метода контурных токов, метода узловых потенциалов. Матричные вычисления выполняются в системе MathCad. Получить токи тех ветвей исходной схемы, в которых было выполнено преобразование. Значения, полученные по методу контурных токов и методу узловых потенциалов, свести в одну таблицу. В системе MathCad отдельно просуммировать генерируемые и потребляемые мощности. Полученные значения сравнить. Исключить из исходной схемы сопротивление R1. Определить эквивалентную ЭДС и эквивалентное внутреннее сопротивление, используя теорему об эквивалентном генераторе. Для нахождения эквивалентной ЭДС воспользоваться методом узловых потенциалов. Для нахождения эквивалентного внутреннего сопротивления воспользоваться методом контурных токов. Найти ток I1. Примечание: при невозможности выполнения расчетов в MathCad, расчет может быть выполнен вручную. Таблица 1 – Исходные данные для расчета Вар. Рис. R1 R2 R3 R4 R5 R6 E1 E2 E3 J1 J2 J3 Ом B A 2 2.1 13 5 2 8 11 15 12 16 0 2 Рисунок 1 – Исходная электрическая цепь Отчет по лабораторной работе должен включать: титульный лист задание порядок выполнения лабораторной работы, в который помещены схемы, все промежуточные расчеты и результаты выводы по работе список использованных источников Отчет сдается в распечатанном или рукописном виде, выполненном аккуратно. Задание принял к исполнению /Ужеков С.С./14.10.2011 Упростим исходную схему. Так как значение J1 равно нулю, ток через ветвь J1 не течет. Эту ветвь исключаем из данной по условию цепи. Расставим токи: Рисунок 2 – Исходная схема с обозначенными токами без ветви J1 Заменим источники токи эквивалентным ЭДС. В данном случае имеется один активный источник тока – J3, заменим его эквивалентным ЭДС E4. Рисунок 3 – Схема после замены источника тока J3 источником ЭДС E4 Заменим источники ЭДС E3 и E4 эквивалентным E34. Рисунок 4 – Схема после замены источниковE1 и E3 эквивалентным E13 Составим систему уравнений по законам Кирхгофа: В данной разветвленной цепи имеется 4 узла, 6 ветвей, 6 контуров. Рисунок 5 – Узлы на схеме Составим У-1=4-1=3 уравнения по первому закону Кирхгофа относительно узлов: По второму закону В-У+1=6+4-1=3 уравнений относительно контуров: Всего уравнений в системе 6 – равно количеству ветвей. Найдем токи методом контурных токов: Примем для 3-х контуров одинаковое направление обхода по часовой стрелке и обозначим на схеме контурные токи: Рисунок 6 –Контурные токи на схеме Выразим контурные токи через токи свободных ветвей: Составим матрицу по методу контурных токов: Решив матрицу методом Крамера, найдем контурные токи: Найдем токи свободных ветвей: Токи смежных ветвей из1-го закона Кирхгофа: Найдем токи методом узловых потенциалов: Для нахождения токов методом узловых потенциалов обозначим на схеме узлы: Рисунок 7 – Обозначение узлов на схеме Потенциал φ0 примем равным 0. Составим матрицу по методу узловых потенциалов: Найдем узловые потенциалы, решив её методом Крамера: Зная значения узловых потенциалов, найдем токи по закону Ома для участка цепи: Сравним результаты: Сравним результаты, полученные с помощью методов контурных токов и узловых потенциалов и в программе MicroCap: Таблица 2 – Сравнение полученных результатов Ток Метод контурных токов Метод узловых потенциалов MicroCap I1 0.805 A 0.805 A 804.937 mA I2 0.172 А 0.172 А 171.995 mA I3 0.977 A 0.977 A 976.932 mA I4 0.299 A 0.299 A 299.474 mA I5 0.471 A 0.471 A 471.469 mA I6 0.505 A 0.505 A 505.463 mA Рисунок 8 – Расчет токов в MicroCap Рисунок 9 – Расчет напряжений в MicroCap Результаты при сопоставлении оказались практически одинаковыми (в MicroCap расчет точнее), можно сказать, что токи рассчитаны верно. Баланс мощностей: Ток J3_1 данной по условию цепи, который исключается при замене источника тока J3 эквивалентным ЭДС, найдем по первому закону Кирхгофа: Баланс мощностей для схемы, данной по условию. Сумма генерируемой мощности: Сумма потребляемой мощности: Суммы генерируемой и потребляемой мощности равны. Значит, баланс сошелся. Рисунок 10 – Расчет мощностей в MicroCap Метод эквивалентного генератора: Найдем ток I1 методом эквивалентного генератора: Рисунок 11 – Суть метода эквивалентного генератора Мысленно исключим из схемы ветвь с током I1 и рассчитаем эквивалентное ЭДС Eekv и эквивалентное сопротивление Rekv: Рисунок 12 – Схема, из которой исключили ветвь с током I1 Эквивалентное ЭДС равно разности потенциалов на зажимах исключенной ветви. Но так как φ0 и φ1 больше не являются узлами, нужно обозначить оставшиеся узлы как φ1’ и φ0’ (где φ0’=0) и найти потенциалы этих точек. Затем найти потенциал точек φ0 и φ1, выразив их через потенциалы φ1 и φ0, использую закон Ома. Для того чтобы найти φ1’, составим матричное уравнение по методу узловых потенциалов: В новой цепи протекают новые токи: Рисунок 13 – Новые токи в цепи – I23 и I46 Найдем потенциал на зажимах ветви с током I1: Найдем эквивалентное ЭДС: Найдем эквивалентное сопротивление: Рисунок 14 – Схема без ветви I1 и без источников Сопротивления R2, R4, R5 представляют собой «звезду». Произведем замену «звезда-треугольник» и найдем сопротивления образовавшегося «треугольника»: Рисунок 15 – После замены «звезда-треугольник» Заменим последовательно соединенные сопротивления R24 и R45 эквивалентным сопротивлением R245, а R3 и R6 – также последовательно соединенные – сопротивлением R36. Рисунок 16 – Схема после замены последовательно соединенных сопротивлений R24, R45, и R3, R6 соответственно эквивалентными R245 и R36 Заменим параллельно соединенные R25, R245 эквивалентным сопротивлением R2245: Затем найдем Rekv: Найдем в итоге ток I1: Выводы: В данной лабораторной работе я изучил и рассчитал токи различными методами: методом контурных токов, методом узловых потенциалов, получил ток I1 методом эквивалентного генератора (активного двухполюсника). Сделал баланс мощностей для схемы с источником тока. Результаты от различных методов практически совпали, баланс мощностей сошелся. Список литературы: Патрушев Е.М. Методические указания по выполнению лабораторных работ по дисциплине «Общая электротехника»/ Е.М. Патрушев, Т.В. Патрушева; Алт.гос.техн.ун-т им. И. И. Ползунова. – Барнаул: Изд-во АтлГТУ, 2009. – 39с. Общая электротехника – электронный учебно-методический комплекс [Электронный ресурс]. – Режим доступа: http://it.fitib.altstu.ru/neud/oe. – Загл. с экрана. studfiles.net mпримеры решений задач / 1.1 Методы расчета электрических цепей / exampl11. Определить токи во всех ветвях схемы методом контурных токов
примеры решений задач / variant_77
7.Построить потенциальную диаграмму для любого замкнутого контура включающего обе ЭДС.
1.1.3 Определить токи во всех ветвях схемы на основании метода наложения
1.1.4 Составить баланс мощностей для заданной схемы
1.1.5 Результаты расчетов токов по пунктам 1 и 2 представить в виде таблицы и сравнить
1.1.6 Построить потенциальную диаграмму для любого замкнутого контура, включающего обе эдс
1.2 Расчет нелинейных электрических цепей постоянного тока Задание
1.8. Расчет цепей методом контурных токов.
1.9. Расчет цепей методом эквивалентного преобразования.
2 2 Ужеков
примеры решений задач / 1.1 Методы расчета электрических цепей / exampl11
| R1 | R2 | R3 | R'4 | R''4 | R5 | R'6 | R''6 | E2 | E3 | J2 |
| Ом | В | А | ||||||||
| 5 | 9 | 2,5 | 3 | 2 | 4 | 9 | 4,5 | 8,2 | 17,5 | 0,2 |
Найти:
1. Составить на основании законов Кирхгофа систему уравнений для
расчёта токов во всех ветвях схемы и решить ее.
2. Определить токи во всех ветвях схемы методом контурных токов.
3. Определить токи во всех ветвях схемы методом узловых потенциалов.
4. Результаты расчёта токов, проведённого тремя методами, свести
в таблицу и сравнить между собой.
5. Составить баланс мощностей в исходной схеме, вычислив суммарною
мощность источников и суммарную мощность нагрузки.
1. Упростить схему, заменив последовательно и параллельно соединённые резисторы четвёртой и шестой ветвей эквивалентными. Дальнейший расчёт вести для упрощённой схемы.
R1
Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы и решить ее.
Упростим схему, заменив источник тока J2 дополнительной ЭДС.
Составляем уравнения Кирхгофа для упрощенной схемы.
1 закон Кирхгофа 2 закон Кирхгофа
где . где
Решать данную систем рекомендуется с помощью метода Крамера, с приведением матрицы 6х6 к матрице вида 3х3.
3. Определить токи во всех ветвях схемы методом контурных токов.
Запишем общую систему уравнений для метода контурных токов.
Рассчитаем коэффициенты данной системы.
Подставим полученные коэффициенты в исходную систему.
Выразим искомые токи ветвей через контурные токи.
4. Определить токи во всех ветвях схемы методом узловых потенциалов.
По условию задания примем потенциал узла с равным 0 => jс=0.
Запишем общую систему уравнений для метода контурных токов.
Рассчитаем коэффициенты данной системы.
Подставим полученные коэффициенты в исходную систему
5. Результаты расчёта токов, проведённого тремя методами, свести в таблицу и сравнить между собой.
| I1 | I2 | I3 | I4 | I5 | I6 | |
| A | ||||||
| метод основанный на законах Кирхгофа | … | … | … | … | … | … |
| метод контурных токов | 0,7888 | 0,9116 | 2,7018 | 1,0014 | 1,7004 | 1,913 |
| метод узловых потенциалов | 0,7888 | 0,9116 | 2,7018 | 1,0014 | 1,7004 | 1,9131 |
| относительная погрешность ( %) | 0 | 0 | 0 | 0 | 0 | 5,227*10-3 |
6. Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).
studfiles.net
Расчет из методички образец
АНАЛИЗ ЭЛЕКТРИЧЕСКОГО СОСТОЯНИЯ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
1.1. Расчет линейных электрических цепей постоянного тока
Задание
Для электрической цепи (рис. 1.1—1.30) выполнить следующее:
1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;
2) определить токи во всех ветвях схемы, используя метод контурных токов;
3) определить токи во всех ветвях схемы на основании метода наложения;
4) составить баланс мощностей для заданной схемы;
5) результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить;
6) определить ток во второй ветви методом эквивалентного генератора;
7) построить потенциальную диаграмму для любого замкнутого кон- тура, включающего обе ЭДС.
Вариант задания определяют по табл. 1.1.
Таблица 1.1
Числовые параметры схем электрических цепей
постоянного тока
| № варианта | Е1 | Е2 | R1 | R2 | R3 | R4 | R5 | R6 | r01 | r02 |
| В | В | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | |
| 0 | 40 | 30 | 52 | 24 | 43 | 36 | 61 | 16 | 1 | 2 |
| 1 | 50 | 30 | 53 | 34 | 24 | 18 | 25 | 42 | 1 | 1 |
| 2 | 20 | 30 | 54 | 43 | 32 | 26 | 51 | 15 | 2 | 2 |
| 3 | 20 | 40 | 64 | 48 | 32 | 25 | 51 | 15 | 1 | 2 |
| 4 | 40 | 20 | 35 | 52 | 24 | 41 | 16 | 61 | 2 | 1 |
| 5 | 30 | 20 | 45 | 53 | 32 | 24 | 61 | 15 | 1 | 1 |
| 6 | 30 | 40 | 26 | 64 | 43 | 35 | 51 | 16 | 2 | 2 |
| 7 | 20 | 30 | 64 | 43 | 31 | 25 | 52 | 14 | 1 | 2 |
| 8 | 30 | 40 | 16 | 63 | 34 | 42 | 25 | 52 | 3 | 2 |
| 9 | 30 | 20 | 54 | 42 | 23 | 31 | 16 | 51 | 1 | 2 |
Примечание. Номер схемы соответствует порядковому номеру, под которым фамилия учащегося записана в журнале учебных занятий группы.
Числовые параметры схемы соответствуют последней цифре ее порядкового номера.
Варианты схем электрических цепей постоянного тока
1.2. Методика расчета линейных электрических
цепей постоянного тока
Для электрической цепи, изображенной на рис. 1.38, выполнить следующее:
1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;
2) определить токи во всех ветвях схемы, используя метод контурных токов;
3) определить токи во всех ветвях схемы на основании метода наложения;
4) составить баланс мощностей для заданной схемы;
5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить;
6) определить ток во второй ветви методом эквивалентного генератора;
7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Дано: Е1= 40 В, Е2 = 60 В, R1 = 18 Ом,
R2 = 36 Ом, R3 = 16 Ом, R4 = 24 Ом,
R5 = 40 Ом, R6 = 34 Ом, r01 = 2 Ом,
r02 = 4 Ом.
Определить: I1, I2, I3, I4, I5.
1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.
Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.
При расчете данным методом произвольно задаем направление токов в ветвях I1, I2, I3, I4, I5.
Составляем систему уравнений.
В заданной цепи пять ветвей, значит, в системе должно быть пять уравнений (m = 5). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n - 1) независимых уравнений. В нашей цепи три узла (А, В, С), значит, число уравнении n - 1 = 3-1 = 2. Составляем два уравнения для любых 2-х узлов, например, для узлов В и С.
узел В: I1 + I2 = I4
узел С: I3 + I5 = I2
Всего в системе должно быть пять уравнений. Два уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.
Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.
Контур АДСВА - обход по часовой стрелке:
Е2 - E1 = I2 (R2 + r02) – I1 (R1 + r01) + I3(R3 + R6)
Контур ABA'A - обход по часовой стрелке:
E1 = I1(R1+r01)+I4R4
Контур А'СВА' — обход против часовой стрелки:
E2 = I2(R2 + r02)+I4R4 + I5R5
ЭДС в контуре берется со знаком “+”, если направление ЭДС совпадает с обходом контура, если не совпадает – знак “-”.
Падение напряжения на сопротивлении контура берется со знаком “+”, если направление тока в нем совпадает с обходом контура, со знаком “-” если не совпадает.
Мы получили систему из пяти уравнений с пятью неизвестными:
Решив систему, определим величину и направление тока во всех ветвях схемы.
Если при решении системы ток получается со знаком “-” значит его действительное направление обратно тому направлению, которым мы задались.
2) Определить токи во всех ветвях схемы, используя метод контурных токов.
Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.
Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной.
Итак, в заданной цепи (рис. 1.38) можно рассмотреть три контура-ячейки (АДСВА, ABA'А, А'СВА') и ввести для них контурные токи Ik1, Ik2, Ik3.
Контуры-ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.
Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур - ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура
На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:
стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3. в контурах - ячейках. Направление обхода контуров принимаем таким же;
составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.
Подставляем в уравнение численные значения ЭДС и сопротивлений.
или
Сократив первое уравнение на 4, второе – на 4,третие – на 10, получим:
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ1, Δ2, Δ3.
Вычисляем контурные токи:
Действительные токи ветвей:
3) Определить токи во всех ветвях схемы на основании метода наложения.
По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
а) Определяем частные токи от ЭДС E1, при отсутствии ЭДС Е2, т. е. рассчитываем цепь по рис. 1.39.
Показываем направление частных токов от ЭДСЕ1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания"
Ток источника
Применяя формулу разброса и 1-й закон Кирхгофа, вычисляем токи
ветвей:
б) Определяем частные токи от ЭДСE2 при отсутствии ЭДС Е1,т.е. рассчитываем простую цепь по рис. 1.40.
Показываем направление частных токов от ЭДС Е2 и обозначаем их буквой I с двумя штрихами (I"). Рассчитываем общее сопротивление цепи:
Вычисляем ток источника:
Применяя форму разброса и 1-й закон Кирхгофа, вычисляем токи ветвей:
Вычисляем токи ветвей исходной цепи (рис. 1.38), выполняя алгебраическое сложение частных токов, учитывая их направление:
4) Составить баланс мощностей для заданной схемы.
Источники E1 и Е2 вырабатывают электрическую энергию, т. к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:
Подставляем числовые значения и вычисляем
С учетом погрешности расчетов баланс мощностей получился.
5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить.
| Ток в ветви Метод расчета | I1,A | I2,A | I3,A | I4,A | I5,A |
| метод контурных токов метод наложения | 0,624 0,625 | 0,522 0,522 | 0,232 0,232 | 1,146 1,147 | 0,290 0,290 |
Расчет токов ветвей обоими методами с учетом ошибок вычислений практически одинаков.
6) Определить ток во второй ветви методом эквивалентного генератора.
Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.
Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части:потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2служит источником электрической энергии, т. е. генератором). Получается схема замещения (рис. 1.41)
На схеме искомый ток I2 определим по закону Ома для замкнутой цепи:
,
где Еэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ = Uхх.
rэ - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов.
Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.42), т. е. при отключенном потребителеR2 от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину:
Зная Iхх, величины сопротивлений и ЭДС, в схеме можно определить Uхх как разность потенциалов между клеммами а и б. Для этого потенциал точки б будем считать известным и вычислим потенциал точки а.
тогда
Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис. 1.43), при этом ЭДСЕ2 и E1 из схемы исключается, а внутренние сопротивления этих источников r01 и r02 в схеме остаются.
Вычисляем эквивалентное сопротивление схемы (рис. 1.43) относительно зажимов а и б.
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:
т. е. ток в этой ветви получился таким же, как и в пунктах 2 и 3.
7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Возьмем контур АДСВА. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю φА=0 (рис. 1.38).
Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А.
0- проверочная точка. Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, во оси ординат - потенциалы точек с учетом их знака.
studfiles.net
4.2. Метод контурных токов
Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.
Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11и I22- контурные токи.
Рис. 4.2
Токи в сопротивлениях R1и R2равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11и I22, так как эти токи направлены в ветви с R3 встречно.
Порядок расчета
Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:
Перегруппируем слагаемые в уравнениях
(4.4)
(4.5)
Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы
, .
Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.
,
где R12- общее сопротивление между первым и вторым контурами;
R21- общее сопротивление между вторым и первым контурами.
E11= E1и E22= E2- контурные ЭДС.
В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
,
.
Собственные сопротивления всегда имеют знак "плюс".
Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.
В схеме на рис. 4.2
.
Рекомендации
Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам.
Контурные токи желательно направлять одинаково (по часовой стрелке или против).
Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным.
Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.
4.3. Метод узловых потенциалов
Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы φ4= 0.
Запишем уравнение по первому закону Кирхгофа для узла 1.
Рис. 4.3
(4.6)
В соответствии с законами Ома для активной и пассивной ветви
,
где - проводимость первой ветви.
,
где - проводимость второй ветви.
Подставим выражения токов в уравнение (4.6).
(4.7)
где g11= g1+ g2- собственная проводимость узла 1.
Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.
g12= g2- общая проводимость между узлами 1 и 2.
Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.
- сумма токов источников, находящихся в ветвях, сходящихся в узле 1.
Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком "плюс", если от узла - со знаком "минус".
По аналогии запишем для узла 2:
(4.8)
для узла 3:
(4.9)
Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы φ1, φ2, φ3, а затем по закону Ома для активной или пассивной ветви найдем токи.
Если число узлов схемы - n, количество уравнений по методу узловых потенциалов - (n - 1).
Замечание.
Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше.
studfiles.net










Поделиться с друзьями: