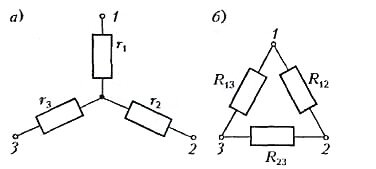
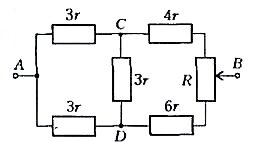
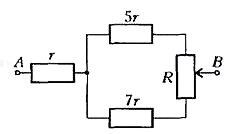
Зильберман А.Р. Преобразование электрических цепей //Квант. — 2002. — № 3. — С. 30-31,34. По специальной договоренности с редколлегией и редакцией журнала "Квант" В этой статье рассказывается о методе, позволяющем упрощать сложные задачи по расчету электрических цепей. Что мы понимаем под «преобразованием цепи»? Предположим, что у нас есть сложная схема из резисторов, имеющая множество выводов и подключенная к источникам. Заменим эту схему другой, но с тем же числом выводов, причем так, чтобы сопротивления между двумя любыми выводами у новой схемы были такими же, как у старой. Ясно, что источники «ничего не узнают» об этой замене и токи, потребляемые схемой, останутся прежними. Но найти эти токи, возможно, окажется проще. Итак, если мы хотим подсчитать токи в сложной схеме, ее можно заменить более простой эквивалентной схемой. При этом токи внутри заменяемой части меняются. Поэтому так поступать можно только с той частью схемы, которая нас непосредственно не интересует. С подобными заменами вы, конечно же, встречались. Пусть, например, в схеме два сопротивления[1]r1 и r2 включены последовательно. Их мы можем заменить одним, равным по величине сумме r1 + r2. Если же два сопротивления включены параллельно, то их также можно заменить одним, величина которого равна \(~\frac{r_1 r_2}{r_1 + r_2}\) . Это — простейшие примеры преобразования цепей. Мы же остановимся на более сложных схемах. Посмотрим, как преобразуются друг в друга схемы, имеющие по три вывода, - «звезда» и «треугольник» (рис.1). Рис. 1 Немного непривычные обозначения на рисунке 1,б очень удобны — индексы показывают, между какими точками включено сопротивление. Например, сопротивление R13 включено между точками 1 и 3 и т.д. Если мы хотим заменить одну из этих схем другой, нужно получить такие соотношения между r и R, чтобы сопротивления между любыми точками были для обеих схем одинаковы. В схеме «звезда» (см. рис. 1, а) сопротивление между точками 1 и 2 равно r1 + r2, а в схеме «треугольник» оно равно \(~\frac{R_{12} (R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . Следовательно, для того чтобы со- противления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы Аналогично, для точек 2 и 3 и для точек 1 и 3: Система уравнений (1) — (3) легко решается. Сложим все уравнения и поделим обе части на 2: Вычтя теперь из этого уравнения уравнение (2), получим Аналогично, и Эти результаты легко запомнить - знаменатель всюду один и тот же, а в числителе справа дважды встречается тот же индекс, что и слева\[~r_1 \to R_{12} R_{13}, r_2 \to R_{12} R_{23}, r_3 \to R_{13} R_{23}\] . Немного сложнее получить формулы для обратного преобразования: но их также легко запомнить - числитель всюду один и тот же, а в знаменателе стоит как раз тот индекс, которого недостает слева. Пользуясь формулами, которые мы только что получили, можно производить замену одной схемы другой. Например, «звезду» с сопротивлениями 1 Ом можно заменить «треугольником» с сопротивлениями 3 Ом (рис.2). Рис. 2 Решим теперь такую задачу: найдем сопротивление между точками A и B в схеме на рисунке 3. Рис. 3 Это обычная схема «мостика», но в нашей задаче «мостик» неуравновешен. Такие задачи приходится решать при помощи правил Кирхгофа. В школьной программе их нет, да и вычисления с помощью этих правил очень громоздкие - в нашем случае получилась бы система пяти уравнений с пятью неизвестными. Мы поступим проще: заменим «треугольник» ACD «звездой», как показано на рисунке 4. Рис. 4 Теперь ясно, что сопротивление между точками A и B будет равно Мы заменяли «треугольник» ACD «звездой», но можно было решать задачу иначе - заменяя «звезду» ADB «треугольником» (проделайте зто самостоятельно). Пусть теперь к точкам A и B подключена батарея с пренебрежимо малым внутренним сопротивлением и ЭДС ε = 1 В. Нужно найти ток через участок СВ. Понятно, что преобразовать схему надо так, чтобы не затронуть интересующее нас сопротивление СВ. Подойдет то преобразование, которое мы делали раньше (см. рис.4). Используя, что \(~R_{AB} = \frac{13}{11}\) Ом , получим После разветвления токи в верхней и в нижней ветвях поделятся в отношении, обратном сопротивлениям ветвей: Отсюда находим Немного сложнее было бы найти ток, идущий через участок CD. Для этого пришлось бы еще найти ток через участок АС, а затем вычесть из него найденный уже ток через участок СВ. Можно еще немного усложнить задачу — учесть внутреннее сопротивление батареи r. Тогда полный ток равен а остальные токи находятся так же, как и раньше. Рис. 5 Рассмотрим более интересную задачу, найдем, при каком соотношении между величинами r и R сопротивление между точками А и В в схеме, показанной на рисунке 5, максимально в крайнем положении движка потенциометра. Рис. 6 Сначала преобразуем схему, заменив «треугольник» ACD «звездой» (рис.6). Очевидно, что сопротивление r не влияет на соотношение сопротивлений в остальной цепи. Займемся поэтому оставшейся частью схемы. Тут включены параллельно два сопротивления: 5r + R1 и 7r + R2, где R1 и R2 - сопротивления верхней и нижней частей потенциометра соответственно. При этом сумма сопротивлений 5r + R1, и 7r + R2 остается постоянной. Посмотрим, какими они должны быть, чтобы полное сопротивление было максимальным. Обозначим Тогда общее сопротивление включенных параллельно частей схемы равно Если учесть, что то Это выражение максимально, когда максимален числитель. Но \(~y = cr_1 - r^2_1\) - это уравнение параболы, ветви которой пересекают ось абсцисс в точках 0 и с. Поэтому числитель дроби наибольший при \(~r_1 = \frac c2\). Так как r1 + r2 = с, то это означает, что сопротивление между точками А и В максимально, если r1 = r2, т.е. Ясно, что это возможно лишь в том случае, если сопротивление всего потенциометра R = R1 + R2 не меньше чем 2r. В противном же случае максимум сопротивления между точками A и B достигается, когда движок потенциометра находится в крайнем положении. Итак, ответ: R ≤ 2r. Метод, о котором мы рассказали, очень удобен для последовательного преобразования сложной схемы к простому виду. Он позволяет рассчитать практически любую сложную цепь, состоящую из сопротивлений. Однако его можно применять и к цепям, содержащим не только сопротивления. Обратим внимание на то, что мы вообще не говорили нигде о физических процессах в цепи, а пользовались только формальным выражением для закона Ома: U = rI. Из него следует, что при последовательном соединении сопротивлений их величины складываются, а при параллельном - складываются величины, обратные сопротивлениям. Понятно, что если какие-нибудь другие физические величины связаны законом, аналогичным закону Ома, то все наши выводы справедливы и для них. Рис. 7 В качестве примера рассмотрим цепь с конденсатором (рис.7). Мы знаем, что заряд конденсатора Q связан с его емкостью C и напряжением на нем U соотношением Сравним последнее выражение с выражением для закона Ома U = rI. Видно, что законы похожи, только вместо тока стоит заряд, а вместо сопротивления-величина, обратная емкости. Это означает, что для того чтобы найти, скажем, заряды на конденсаторах, можно поступить так: вместо цепи, содержащей конденсаторы, нарисовать цепь, содержащую сопротивления, причем конденсатор емкостью C(Ф) заменить сопротивлением \(~r = \frac 1C\) (Ом). После того как мы рассчитаем токи в цепи из сопротивлений, можно сразу записать, каковы заряды на конденсаторах: если по сопротивлению течет ток I = х (А), то на соответствующем конденсаторе будет заряд Q = х (Кл). ЭДС батарей при таком преобразовании цепи остаются без изменения. Но, разумеется, в цепи с конденсаторами внутренние сопротивления батарей не влияют на результат. Поэтому, преобразуя цепь, нам придется лишить батареи их внутренних сопротивлений. Пусть, например, нужно найти заряд на конденсаторе емкостью 10 мкФ в схеме, изображенной на рисунке 8. Конденсатору емкостью С = 2 мкФ = 2·10-6 Ф соответствует сопротивление r = 5·105 Ом = 500 кОм. Далее расчет проводится уже достаточно просто (проделайте это самостоятельно). Рис. 8 Таким образом, метод преобразования цепей, как мы видим, пригоден и для схем из конденсаторов. www.physbook.ru Расчет обычных цепей неизменного тока Под эквивалентными преобразованиями в электронной цепи предполагается подмена одних частей другими таким макаром, чтоб электрические процессы в ней не поменялись, а схема упрощалась. Одним из видов таких преобразований является подмена нескольких потребителей, включённых поочередно либо параллельно, одним эквивалентным. Несколько поочередно соединённых потребителей можно поменять одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых поочередно. Для n потребителей можно записать: rэ = r1 +r2+…+rn , где r1 , r2, …, rn – сопротивления каждого из n потребителей. При параллельном соединении n потребителей эквивалентная проводимость gэ равна сумме проводимостей отдельных частей, включённых параллельно: gэ= g1 + g2 +…+ gn . Беря во внимание, что проводимость является оборотной величиной по отношению к сопротивлению, можно эквивалентное сопротивление найти из выражения: 1/rэ = 1/r1 + 1/r2 +…+ 1/rn, где r1, r2, …, rn – сопротивления каждого из n потребителей, включённых параллельно. В личном случае, когда параллельно включены два потребителя r1 и r2, эквивалентное сопротивление цепи: rэ = (r1 х r2)/(r1 + r2) Преобразования в сложных цепях, где отсутствует в очевидном виде последовательное и параллельное соединение частей (набросок 1), начинают с подмены частей, включённых в начальной схеме треугольником, на эквивалентные элементы, соединённые звездой. Набросок 1. Преобразование частей цепи: а — соединённых треугольником, б — в эквивалентную звезду На рисунке 1, а треугольник частей образуют потребители r1, r2, r3. На рисунке 1, б этот треугольник заменён эквивалентными элементами ra, rb, rc, соединёнными звездой. Чтоб не происходило изменение потенциалов в точках a, b, с схемы, сопротивления эквивалентных потребителей определяются из выражений: Упрощение начальной цепи можно также выполнить подменой частей, соединённых звездой, схемой, в какой потребители соединены треугольником. В схеме, изображённой на рисунке 2, а, можно выделить звезду, образованную потребителями r1, r3, r4. Эти элементы включены меж точками c, b, d. На рисунке 2, б меж этими точками находятся эквивалентные потребители rbc, rcd, rbd, соединённые треугольником. Сопротивления эквивалентных потребителей определяются из выражений: Набросок 2. Преобразование частей цепи: а — соединённых звездой, б — в эквивалентный треугольник Предстоящее упрощение схем, приведённых на рисунках 1, б и 2, б, можно производить оковём подмены участков с поочередным и параллельным соединением частей их эквивалентными потребителями. При практической реализации способа расчёта обычный цепи при помощи преобразований выявляются в цепи участки с параллельным и поочередным соединением потребителей, а потом рассчитываются эквивалентные сопротивления этих участков. Если в начальной цепи в очевидном виде нет таких участков, то, применяя описанные ранее переходы от треугольника частей к звезде либо от звезды к треугольнику, проявляют их. Данные операции позволяют упростить цепь. Применив их пару раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Дальше, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи. Расчет сложных цепей неизменного тока В процессе расчёта сложной цепи нужно найти некие электронные характеристики (сначала токи и напряжения на элементах) на базе начальных величин, данных в условии задачки. На практике употребляются несколько способов расчёта таких цепей. Для определения токов веток можно использовать: способ, базирующийся на основании конкретного внедрения законов Кирхгофа, способ контурных токов, способ узловых напряжений. Для проверки корректности вычисления токов нужно составить баланс мощностей. Из закона сохранения энергии следует, что алгебраическая сумма мощностей всех источников питания цепи равна арифметической сумме мощностей всех потребителей. Мощность источника питания равна произведению его ЭДС на величину тока, протекающего через данный источник. Если направление ЭДС и тока в источнике совпадают, то мощность выходит положительной. В неприятном случае она отрицательна. Мощность потребителя всегда положительна и равна произведению квадрата тока в потребителе на величину его сопротивления. Математически баланс мощностей можно записать в последующем виде: где n – количество источников питания в цепи; m – количество потребителей. Если баланс мощностей соблюдается, то расчет токов выполнен верно. В процессе составления баланса мощностей можно узнать, в каком режиме работает источник питания. Если его мощность положительна, то он дает энергию во внешнюю цепь (к примеру, как аккумулятор в режиме разряда). При отрицательном значении мощности источника последний потребляет энергию из цепи (аккумулятор в режиме заряда). Пацкевич В. А. Школа для электрика elektrica.info В ряде случаев расчет сложной электрической цепи упрощается, если в ее схеме замещения заменить группу резистивных элементов другой эквивалентной группой, в которой эти элементы соединены иначе. Взаимная эквивалентность заключается в том, что после замены режим работы остальной части цепи не изменится. Метод может быть успешно применен для расчета таких цепей, в которых имеются резисторы, включенные между собой последовательно, параллельно или по смешанной схеме. Смешанным соединением называют такое соединение нескольких элементов, при котором в схеме можно выделить участки с последовательным и параллельным соединением. Так на схеме, изображенной на рисунке 1.11(а), резисторы R3 и R4 включены последовательно: между ними, в точке 3 нет ответвления с током, поэтому I3=I4. Эти два резистора можно заменить одним, эквивалентным, определив его как сумму R3+R4=R34 После такой замены получается более простая схема (рис. 1.11(б). Здесь следует обратить внимание на возможные ошибки в определении способа соединения резисторов, которые иногда допускаются при отсутствии опыта в расчете электрических цепей. Например, резисторы R1 и R3 ошибочно принимают соединенными последовательно, а резисторы R2 и R4 – соединенными параллельно. Такое определение способа соединения резисторов не соответствует основным признакам последовательного и параллельного соединения. Между резисторами R1 и R3 , в точке 2, имеется ответвление с током I2. Поэтому ток I1 не может быть равен току I3, а резисторы R1 и R3 нельзя считать включенными последовательно. Резисторы R2 и R4 с одной стороны присоединены к общей точке 4, а с другой стороны – к разным точкам схемы 2 и 3. Следовательно, напряжение, приложенное к резистору R2, не может быть одновременно и напряжением на резисторе R4. Поэтому резисторы R2 и R4 нельзя считать включенными параллельно. Рисунок 1.11 – Расчет цепи методом эквивалентного преобразования схем Параллельно соединены резистор R2 и последовательная группа резисторов R3 и R4, т.е. эквивалентное сопротивление R34, что более наглядно видно из схемы, представленной на рисунке 1.11(б). Сопротивления резисторов R2 и R34 можно заменить одним, эквивалентным, определив его из выражения и получить более простую схему (рис.1.11(в). В схеме на рисунке 1.11(в) резисторы R1, R24, R5 соединены последовательно. Заменив их одним, эквивалентным, получим простейшую схему (рис. 1.11(г). Подобными преобразованиями схему смешанного соединения резисторов с одним источником энергии в большинстве случаев удается привести к простейшей схеме, что значительно облегчает расчет. В схеме рисунка 1.11(г) ток I1 определяется по закону Ома. Токи в других ветвях первоначальной схемы нетрудно определить, переходя от схемы к схеме в обратном порядке. Из схемы на рисунке 1.11,в наглядно видно, что I5=I1=I2+I3. Кроме того, напряжение между точками 2 и 4 U24=I1R24. Зная это напряжение, легко определить токи I2 и I3=I4: I2=U24/R2; I3=I4=U24/R34. Следует иметь в виду, что в некоторых электрических цепях резисторы могут быть включены не последовательно и не параллельно, а образовывать контуры, которые называют треугольниками сопротивлений. В этом случае свернуть схему до простейшей удается, применив преобразование треугольника сопротивлений в эквивалентную трехлучевую звезду. При этом сопротивления эквивалентной звезды (рис.1.12) могут быть пересчитаны через сопротивления треугольника при помощи формул: Рисунок 1.12 – Преобразование треугольника сопротивлений в эквивалентную звезду Возможна и обратная замена трехлучевой звезды эквивалентным треугольником: При расчете цепи этим методом полагают, что в каждом независимом контуре электрической цепи течет свой контурный ток. Записывают уравнения по второму закону Кирхгофа для контурных токов и, решая эти уравнения, находят контурные токи. Затем через контурные токи определяют действительные токи ветвей. Вывод основных расчетных уравнений приведем применительно к схеме, изображенной на рисунке 1.13, в которой имеется два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток I11, а в правом (также по часовой стрелке) – контурный ток I22. Рисунок 1.13 – Расчет цепи методом контурных токов Запишем уравнения по второму закону Кирхгофа для каждого из контуров. При этом учтем, что в смежной ветви (с резистором R5) сверху вниз течет ток равный I11-I22. Направления обхода контуров примем также по часовой стрелке. Для левого контура: Для правого контура: После элементарных преобразований получаем: Рассмотрим коэффициенты при искомых токах. В первом уравнении коэффициент при токе I11 представляет собой сумму сопротивлений первого контура. Обозначим его R11. Коэффициент при токе I22 – сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус. Обозначим его R12. Аналогично, во втором уравнении коэффициент при токе I11 представляет собой взятое со знаком минус сопротивление смежной ветви между вторым и первым контурами (R21). Коэффициент при токе I22 представляет собой суммарное сопротивление второго контура – R22. В правой части первого уравнения имеем контурную ЭДС первого контура E11, а в правой части второго уравнения – контурную ЭДС второго контура – Е22. Перепишем исходные уравнения с учетом принятых обозначений: Если в цепи имеется больше двух контуров, например, три, то система уравнений выглядит следующим образом: или в матричной форме: Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например, по часовой стрелке. Решение системы уравнений дает искомые контурные токи. В ветвях, не являющихся смежными между соседними контурами (например, в ветви с резисторами R1, R2 схемы рис.1.13), найденный контурный ток является действительным током ветви. В смежных ветвях действительные токи определяются через контурные. Например, в ветви с резистором R5 протекающий сверху вниз ток равен разности I11-I22. Рассмотрим пример: по заданным параметрам цепи и ЭДС источников рассчитать токи ветвей цепи, представленной на рисунке 2.2 методом контурных токов. Находим: R11=R1+R2+R5=2+3+1=6Ом; R22=R5+R3+R4=1+5+3=9Ом; R12=R21=-R5=-1Ом; E11=E1+E5=5+8=13В; E22=-E5-E4==-8-3=-11В. Подставив полученные данные в систему (1.25), находим решение: I11=2A; I22=-1А. Рассчитываем действительные токи ветвей: I1=I11=2А; I5=I11-I22=2+1=3А; I4=-I22=1А. Другие разделы главы 1: chertovlektor.ru Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью. Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут. Допустим, что R1=10 Ом R2=20 Ом, тогда Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1) Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз. В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом) Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно. Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R. R4=20 Ом, R5=40 Ом, R6=15 Ом Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник. electroandi.ruРасчет сопротивления цепи. Как упростить схему электрической цепи
Kvant. Преобразование эл. цепей — PhysBook





Примечания
Расчет электрических цепей постоянного тока
 Целью расчёта электронной цепи неизменного тока является определение неких характеристик на базе начальных данных, из условия задачки. На практике употребляют несколько способов расчёта обычных цепей. Какой-то из них базируется на применении эквивалентных преобразований, позволяющих упростить цепь.
Целью расчёта электронной цепи неизменного тока является определение неких характеристик на базе начальных данных, из условия задачки. На практике употребляют несколько способов расчёта обычных цепей. Какой-то из них базируется на применении эквивалентных преобразований, позволяющих упростить цепь. 




Расчет цепей постоянного тока
/ 1.9.1 Метод эквивалентного преобразования схем
1.9.2 Метод контурных токов
Расчет сопротивления цепи
Пример 1


Пример 2


Пример 3


Пример 4


Пример 5


интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''









Поделиться с друзьями: