Электрическая схема — это условное графическое изображение электрической цепи. Различают следующие виды электрических схем: структурные (функциональные), принципиальные и эквивалентные. Структурной (функциональной) электрической схемой называется условное графическое изображение цепи, на котором показаны основные функциональные части цепи (блоки, каскады и пр.) и связи между ними. Принципиальной электрической схемой называется условное графическое изображение реальной цепи, на котором с помощью условных обозначений показаны все элементы цепи и соединения между ними. Эквивалентной электрической схемой называется схема, составленная путём замены реальных элементов принципиальной электрической схемы их идеализированными эквивалентами. Условные графические изображения и буквенные обозначения элементов, используемые при составлении принципиальных и эквивалентных электрических схем, определяются действующими стандартами единой системы конструкторской документации (ЕСКД). Лекция № 2 Тема 2. Идеализированные элементы электрической цепи Сопротивление Сопротивлением называется идеализированный элемент цепи, способный необратимо преобразовывать электрическую энергию в другой вид энергии (тепловую, механическую и пр.). С этой точки зрения сопротивление является пассивным (диссипативным, то есть рассеивающим энергию) элементом электрической цепи. Условное графическое изображение сопротивления показано на рис 2.1. Основной характеристикой сопротивления является вольтамперная характеристика, которая представляет собой зависимость напряжения на выводах сопротивления от проходящего через него тока (рис 2.2). Если вольтамперная характеристика сопротивления линейна (рис. 2.2, 2), то в этом случае сопротивление называют линейным, а его статическое и динамическое сопротивления одинаковы Уравнение, связывающее ток и напряжение линейного сопротивления, определяется законом Ома, который был установлен Омом экспериментальным путём в 1826 г, Величина обратная сопротивлению называется проводимостью и обозначается буквой В Международной системе единиц СИ сопротивление измеряется в омах (Ом), а проводимость — в сименсах (См). Поэтому сопротивление резисторов часто называют омическим Мгновенная мощность, поступающая в сопротивление, всегда является положительной вещественной величиной Электрическая энергия, поступающая в сопротивление и преобразующаяся в нём в другие виды энергии (тепловую, механическую и т.п.), также является положительной вещественной величиной Мкость Емкостью называется идеализированный элемент электрической цепи, способный запасать энергию электрического поля. Условное графическое изображение емкости показано на рис. 2.3. При этом каждой точке характеристики ставится в соответствие статическая ёмкость Если кулон-вольтная характеристика ёмкости является линейно (рис. 2.4, 2), то такая ёмкость называется линейной, её статическая и динамическая емкости равны и не зависят от напряжения на ёмкости и запасённого в ней заряда В Международной системе единиц СИ емкость измеряется в фарадах (Ф = Кл/В). Тогда заряд линейной ёмкости Подставляя (2.3) в (1.1), находим ток линейной емкости Если напряжение на емкости не изменяется во времени Преобразуя (2.4), найдём напряжение ёмкости: В последнем выражении нижний предел интегрирования равен где Определим мгновенную мощность электрического поля ёмкости Приравнивая правые части уравнений (1.3) и (2.6), находим Откуда получаем, что энергия электрического поля, запасенная ёмкостью, в произвольный момент времени определяется выражением и всегда имеет положительное значение. Когда заряд ёмкости увеличивается, электрическая энергия из внешней цепи поступает в ёмкость, где она запасается в виде энергии электрического поля. О таком процессе говорят, что ёмкость заряжается. Когда заряд ёмкости уменьшается, ёмкость отдает накопленную энергию во внешнюю цепь. О таком процессе говорят, что ёмкость разряжается. Поскольку при этом никакого преобразования электрической энергии в другие виды энергии не происходит, то с энергетической точки зрения идеализированная ёмкость является пассивным энергоёмким или реактивным элементом электрической цепи. Индуктивность Индуктивностью называется идеализированный элемент электрической цепи, способный запасать энергию магнитного поля. Условное графическое изображение индуктивности показано на рис. 2.5. В соответствии с законом электромагнитной индукции Фарадея э.д.с., наводимая в индуктивности, где В общем случае магнитный поток, пронизывающий где Поэтому в общем случае потокосцепление индуктивности состоит из двух составляющих где В результате, э.д.с., наведенная в индуктивности, может быть представлена в виде где Тогда потокосцепление прямо пропорционально току индуктивности Если индуктивность линейная и отсутствует внешнее потокосцепление, то э.д.с. самоиндукции, наводимая в индуктивности, определяется с учётом (2.8) и (2.9) по формуле При анализе цепей положительное направление напряжения на выводах индуктивности выбирают совпадающим с положительным направлением тока, то есть противоположным направлению э.д.с. самоиндукции (рис. 2.5), Из (2.10) следует, что при протекании через индуктивность постоянного тока напряжение на индуктивности равно нулю и, следовательно, её сопротивление на постоянном токе также равно нулю. Решая уравнение (2.10) относительно тока В последнем выражении нижний предел интегрирования равен где С учётом (2.10) определим мгновенную мощность индуктивности Приравнивая правые части уравнений (1.3) и (2.12), находим Откуда следует, что энергия магнитного поля, запасенная индуктивностью, в произвольный момент времени определяется выражением и всегда имеет положительное значение. Таким образом, с энергетической точки зрения индуктивность является пассивным элементом электрической цепи, который при возникновении в нем электрического тока запасает энергию в виде энергии магнитного поля и отдает эту энергию в процессе исчезновения этого тока. Поэтому идеализированные индуктивность называют пассивным энергоемким или реактивным элементом электрической цепи по аналогии с идеальной ёмкостью. Линейные и нелинейные электрические цепи. Электрической схемой называют
Электрическая схема
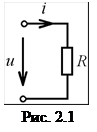 Термин «сопротивление» и соответствующее ему условное обозначение
Термин «сопротивление» и соответствующее ему условное обозначение  используется в расчётных формулах для обозначения сопротивления как физической величины, а также в электрических схемах для обозначения резистора как элемента цепи. Наиболее близким к идеализированному сопротивлению по своим характеристикам является резистор.
используется в расчётных формулах для обозначения сопротивления как физической величины, а также в электрических схемах для обозначения резистора как элемента цепи. Наиболее близким к идеализированному сопротивлению по своим характеристикам является резистор.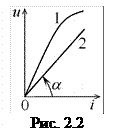 Если вольтамперная характеристика сопротивления является нелинейной (рис 2.2, 1), то такое сопротивление называют нелинейным. При этом каждая точке вольтамперной характеристики ставится в соответствие статическое сопротивление
Если вольтамперная характеристика сопротивления является нелинейной (рис 2.2, 1), то такое сопротивление называют нелинейным. При этом каждая точке вольтамперной характеристики ставится в соответствие статическое сопротивление  и динамическое сопротивление
и динамическое сопротивление  , которые в общем случае не равны между собой
, которые в общем случае не равны между собой  .
. и не зависят от напряжения и тока сопротивления.
и не зависят от напряжения и тока сопротивления. ;
;  ,
, 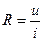 . (2.1)
. (2.1)
 .
. . (2.2)
. (2.2)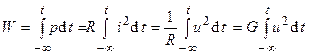 .
.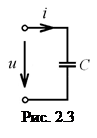 Наиболее близким к идеализированной емкости является конденсатор. Термин «ёмкость» и соответствующее ему условное обозначение
Наиболее близким к идеализированной емкости является конденсатор. Термин «ёмкость» и соответствующее ему условное обозначение 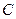 используется в расчётных формулах для обозначения ёмкости как физической величины, а также в электрических схемах для обозначения конденсатора как элемента цепи.
используется в расчётных формулах для обозначения ёмкости как физической величины, а также в электрических схемах для обозначения конденсатора как элемента цепи.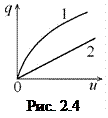 Основной электрической характеристикой ёмкости является кулон-вольтная характеристика, которая представляет собой зависимость заряда
Основной электрической характеристикой ёмкости является кулон-вольтная характеристика, которая представляет собой зависимость заряда  , накопленного в ёмкости, от напряжения
, накопленного в ёмкости, от напряжения  на её выводах (рис 2.4) Если эта характеристика является нелинейной (рис 2.4, 1), то такая ёмкость называется нелинейной.
на её выводах (рис 2.4) Если эта характеристика является нелинейной (рис 2.4, 1), то такая ёмкость называется нелинейной.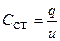 и динамическая ёмкость
и динамическая ёмкость 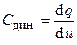 , которые в общем случае не равны друг другу
, которые в общем случае не равны друг другу  .
. .
. . (2.3).
. (2.3).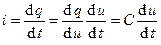 . (2.4).
. (2.4).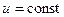 , то в ёмкости существует постоянное электрическое поле. При этом из (2.4) следует, что ток емкости равен нулю, и, следовательно, её сопротивление на постоянном токе бесконечно велико. Если напряжение на емкости изменяется во времени, то в ёмкости существует переменное электромагнитной поле, которое движется внутри емкости от одной его обкладки к другой. При этом в цепи, подключенной к ёмкость, идёт переменный электрический ток, который называют током ёмкости.
, то в ёмкости существует постоянное электрическое поле. При этом из (2.4) следует, что ток емкости равен нулю, и, следовательно, её сопротивление на постоянном токе бесконечно велико. Если напряжение на емкости изменяется во времени, то в ёмкости существует переменное электромагнитной поле, которое движется внутри емкости от одной его обкладки к другой. При этом в цепи, подключенной к ёмкость, идёт переменный электрический ток, который называют током ёмкости.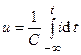 .
. , что позволяет учесть все изменения заряда в ёмкости, как бы давно они ни происходили. Если наблюдение за напряжением ёмкости начинается с некоторого момента времени
, что позволяет учесть все изменения заряда в ёмкости, как бы давно они ни происходили. Если наблюдение за напряжением ёмкости начинается с некоторого момента времени  , то последний интеграл можно представить в виде суммы
, то последний интеграл можно представить в виде суммы , (2.5)
, (2.5)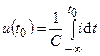 — начальное напряжение на ёмкости в момент времени
— начальное напряжение на ёмкости в момент времени 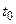 .
. . (2.6)
. (2.6)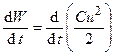 .
.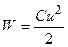 (2.7)
(2.7)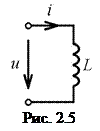 Наиболее близким к идеализированной индуктивности является катушка индуктивности без ферромагнитного сердечника. Термин «индуктивность» и соответствующее ему условное обозначение
Наиболее близким к идеализированной индуктивности является катушка индуктивности без ферромагнитного сердечника. Термин «индуктивность» и соответствующее ему условное обозначение 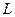 используется в расчётных формулах для обозначения индуктивности как физической величины, а также в электрических схемах для обозначения катушки индуктивности как элемента цепи.
используется в расчётных формулах для обозначения индуктивности как физической величины, а также в электрических схемах для обозначения катушки индуктивности как элемента цепи.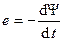 , (2.8)
, (2.8) — потокосцепление индуктивности;
— потокосцепление индуктивности; 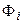 — магнитный поток, пронизывающий
— магнитный поток, пронизывающий  -й виток индуктивности;
-й виток индуктивности;  — число витков индуктивности.
— число витков индуктивности. -й виток индуктивности, можно представить в виде
-й виток индуктивности, можно представить в виде ,
,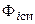 — магнитный поток самоиндукции, который вызван электрическим током, протекающим в индуктивности;
— магнитный поток самоиндукции, который вызван электрическим током, протекающим в индуктивности; 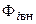 — внешний магнитный поток, обусловленный внешними источниками магнитного поля.
— внешний магнитный поток, обусловленный внешними источниками магнитного поля. ,
, — потокосцепление самоиндукции;
— потокосцепление самоиндукции; 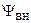 — внешнее потокосцепление.
— внешнее потокосцепление.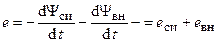 .
. — э.д.с. самоиндукции, вызванная изменением потокосцепление самоиндукции;
— э.д.с. самоиндукции, вызванная изменением потокосцепление самоиндукции; 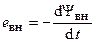 — э.д.с., вызванная изменением внешнего потокосцепления.
— э.д.с., вызванная изменением внешнего потокосцепления.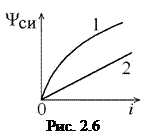 Зависимость потокосцепления самоиндукции от тока индуктивности называется вебер-амперной характеристикой. Если эта характеристика является нелинейной (рис 2.6, 1), то такая индуктивность называется нелинейной. Каждой точке вебер-амперной характеристики ставится в соответствие статическая индуктивность
Зависимость потокосцепления самоиндукции от тока индуктивности называется вебер-амперной характеристикой. Если эта характеристика является нелинейной (рис 2.6, 1), то такая индуктивность называется нелинейной. Каждой точке вебер-амперной характеристики ставится в соответствие статическая индуктивность  и динамическая индуктивность
и динамическая индуктивность 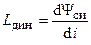 , которые в общем случае не равны между собой
, которые в общем случае не равны между собой 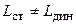 . Если вебер-амперную характеристика линейная (рис 2.6, 2), то индуктивность называют линейной. В этом случае статическая и динамическая индуктивности равны и могут рассматриваться как коэффициент пропорциональности между потокосцеплением и током
. Если вебер-амперную характеристика линейная (рис 2.6, 2), то индуктивность называют линейной. В этом случае статическая и динамическая индуктивности равны и могут рассматриваться как коэффициент пропорциональности между потокосцеплением и током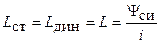 .
. . (2.9).
. (2.9). .
. . (2.10)
. (2.10) , находим
, находим .
. , что позволяет учесть все изменения потокосцепления индуктивности, как бы давно они ни происходили. Если ток индуктивности определяется, начиная с некоторого момента времени
, что позволяет учесть все изменения потокосцепления индуктивности, как бы давно они ни происходили. Если ток индуктивности определяется, начиная с некоторого момента времени  , то последний интеграл можно представить в виде
, то последний интеграл можно представить в виде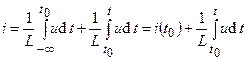 , (2.11)
, (2.11)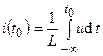 — ток индуктивности в момент
— ток индуктивности в момент 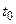 .
.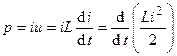 . (2.12)
. (2.12)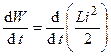 .
.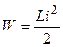 ,. (2.13)
,. (2.13)Похожие статьи:
poznayka.org
Линейные и нелинейные электрические цепи — Мегаобучалка
Ветвь и узел электрической цепи
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. В зависимости от особенностей схемы следует применять тот или иной способ расчета электрической цепи. В данном разделе рассмотрим ключевые понятия, которые в дальнейшем будут необходимы для выбора наиболее оптимального и правильного приема решения задач.
Ветвью называется участок электрической цепи, обтекаемый одним и тем же током. Ветвь образуется одним или несколькими последовательно соединенными элементами цепи.
Узел - место соединения трех и более ветвей.В качестве примера на рисунке изображены схемы двух электрических цепей. Первая из них содержит 6 ветвей и 4 узла. Вторая состоит из 5 ветвей и 3 узлов. В этой схеме обратите внимание на нижний узел. Очень часто допускают ошибку, считая что там 2 узла электрической цепи, мотивируя это наличием на схеме цепи в нижней части 2-х точек соединения проводников. Однако на практике следует считать две и более точки, соединенных между собой проводником, как один узел электрической цепи.
При обходе по соединенным в ветвях цепям можно получить замкнутый контурэлектрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел встречается в данном контуре не более одного раза. Ниже приведена электрическая схема, на которой отмечено несколько произвольно выбранных контуров.
Всего для данной цепи можно выделить 6 замкнутых контуров.
Закон Ома
Данный закон очень удобно применять для ветви электрической цепи. Позволяет определить ток ветви при известном напряжении между узлами, к которым данная ветвь подключена. Также позволяет буквально в одно действие рассчитать одноконтурную электрическую цепь.
При применении закона Ома предварительно следует выбрать направление тока в ветви. Выбор направления можно осуществить произвольно. Если при расчете будет получено отрицательное значение, то это значит, что реальное направление тока противоположно выбранному.Для ветви, состоящей только из резисторов и подключенной к узлам электрической цепиa и b (см. рис.) закон Ома имеет вид:Соотношение (1.15) написано в предположении, что выбрано направление тока в ветви от узла a к узлу b. Если мы выберем обратное направление, то числитель будет иметь вид: (Ub-Ua). Теперь становится понятно, что если в соотношении (1.15) возникнет ситуация, когда Ub>Ua то получим отрицательное значение тока ветви. Как уже упоминалось выше, это значит, что реальное направление тока противоположно выбранному. Примером практического применения данного частного случая закона Ома при расчетах электрических цепей является соотношение (1.18) для электрической цепи, изображенной на рисунке.
Для ветви содержащей резисторы и источники электрической энергии закон Ома принимает следующий вид:Соотношение (1.16) написано в предположении, что предварительно выбрано напавление тока от узла a к узлу b. При расчете алгебраической суммы ЭДС ветви следует знак "+" присваивать тем ЭДС, чье направление совпадает с направлением выбранного тока ветви (направление ЭДС определяется направлением стрелки в обозначении источника электрической энергии). Если направления не совпадают, то ЭДС берется со знаком "-". На рисунке есть примеры применения данного варианта закона Ома - соотношения (1.17) и (1.19)
Если необходимо рассчитать одноконтурную электрическую цепь с произвольным количеством источников электрической энергии и резисторов, то следует применять соотношение (1.16), имея ввиду что Ua=Ub.
Линейные и нелинейные электрические цепи
Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы(подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и катушки индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.
Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту, от напряжения на этом компоненте называется вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.
В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.
Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие толькорезисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.
Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть применён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).
электрическая цепь – это отдельно взятая группа электроприборов (утюги, блоки телевизоры, холодильники и т. д.) совместно с розетками, выключателями, проводами, автоматами и электрической подстанцией (как же без нее получить ток) на данный момент работающих совместно для достижения определенной цели. Ну а вот в зависимости от цели (просмотра любимой передачи, сохранения свежести продуктов или обеспечения стабильности питающих параметров в блоке питания компьютера) электрические цепи подразделяются на простые и сложные, неразветвленные и разветвленные, линейные и нелинейные.
То есть электрическую цепь можно рассматривать как совокупность отдельных электрических устройств, так и совокупность дискретных простейших деталей и связей между ними образующих один из функциональных блоков в электрической схеме какого-то устройства.
Неразветвленныеэлектрические цепи – они же простые – это цепи в которых ток течет не меняя свое значение и по простейшему пути от источника энергии до потребителя. То есть через все элементы этой цепи течет один и тот же ток. Простейшей неразветвленной цепью можно считать цепь освещения одной из комнат в квартире, где используется однорожковая люстра. В данном случае ток течет от источника энергии через автомат, выключатель, лампочку и обратно к источнику энергии.
Разветвленные– это цепи имеющие одно или более ответвленных путей протекания тока. То есть ток начиная свой путь от источника энергии разветвляется на несколько ветвей потребителей, при этом меняя свое значение. Одним из несложных примеров такой цепи является приведенная выше цепь освещения комнаты в квартире, но только с многорожковой люстрой и многоклавишным выключателем. Ток от источника энергии доходит через автомат к многоклавишному выключателю, а дальше разветвляется на несколько ламп люстры, а далее через общий провод обратно к источнику энергии.
Линейной считается такая электрическая цепь, где характеристики всех ее элементов не зависят от величины и характера протекающего тока и приложенного напряжения.
Нелинейной считается цепь содержащая хотя бы один элемент, характеристики которого зависят от протекающего тока и приложенного напряжения.
2. Эквивалентные преобразования в электрических цепях. Определение эквивалентного сопротивления при последовательном, параллельном и смешанном соединении элементов электрических цепей.
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R3. Следует понимать, что после преобразования эквивалентное сопротивление R1R2 и резистор R3, соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R1, R2 и R3.
Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R3,R4 и R5,R2 соединены между друг другом последовательно, а в парах параллельно.
megaobuchalka.ru
1.3.Электрическая схема, топология электрической цепи
Кроме понятия электрической цепи в инженерной практике широкое распространение нашел термин «электрическая схема». В теории цепей схемой называют графическое изображение электрической цепи. Элементам схемы соответствуют активные и пассивные элементы электрической цепи.
В микроэлектронике понятие электрической цепи и электронной схемы часто отождествляют между собой. Так, микросхемой (интегральной схемой) называют интегральную электрическую цепь, содержащую сотни и тысячи простейших активных и пассивных элементов. Чтобы не ломать сложившуюся традицию, будем использовать термин «электрическая схема» или просто «схема» применительно
к графическому изображению электрической цепи или электронной схемы и термины «электрическая цепь» или «электронная (микроэлектронная, интегральная) схема» применительно к моделям реальных физических электрических или электронных устройств.
Для анализа электрических цепей в последнее время все большее распространение находят матрично-топологические методы. В их основе лежит представление электрической схемы с помощью графа цепи. Графом цепи называют геометрическую систему линий (ветвей), соединяющих заданные точки (узлы). Если ветви графа ориентированы по направлению токов ветвей, то граф называется ориентированным (направленным). На рис. 1.11, а изображена электрическая схема и ее ориентированный (рис. 1.11, б) граф. Граф содержит всю информацию о геометрической структуре схемы.
Простым узлом называют место соединения зажимов двух элементов (рис. 1.12, «), а сложным — место соединения зажимов трех и более элементов (рис. 1.12, б).
Ветвью называют часть цепи, включенной между двумя узлами, через которые она обменивается энергией с остальной цепью. Ветви, подсоединенные к одной паре узлов, образуютпараллельное соединение (рис. 1.12, в).
Последовательно соединенные ветви, связывающие два заданиях узла образуют простой путь, если в нем нет повторяющих Узлов. Например, между узлами 1 и 4 (рис. 1.11, б) простой путь
образуется ветвями 3, 5 или 3, 4 и т. д. Замкнутый путь называется контуром (рис. 1.12, в).
Подграфом называют часть графа. Подграф является связным, если любые его два узла связаны, т. е. соединены ветвями.
Деревом графа называют связный подграф, содержащий все узлы, но не содержащий ни одного контура (рис. 1.13). Ветви дерева называют ребрами (на рис. 1.13 показаны сплошными линиями).
В теории графов доказывается, что число ветвей дерева, содержащего «у узлов, определяется уравнением
Совокупность ветвей не входящих в состав дерева, образует его дополнение (на рис. 1.13 помечено штриховыми линиями). Ветви дополнения называют хордами. Можно показать, что число хорд
где пв — общее число ветвей исходного графа.
Сечением графа называют минимальное множество ветвей, удаление которых разбивает граф на две несвязанных части (подграфы). На рис. 1.11, 6 показан пример двух сечений, образованных ветвями 1, 2, 4, 5 (по линии А—А) и 3, 6 (по линии В—В). Добавление любой из ветвей сечения делает граф связным. Обычно сечение изображают в виде замкнутой линии, рассекающей граф цепи на несвязанные компоненты. Сечение, «рассекающее» только одну ветвь дерева, называют главным сечением. Причем, каждому
дереву соответствует своя совокупность главных сечений (рис. 1.13, сечения S1, S2, S3). Число главных сечений равно числу ветвей дерева (1.14).
Аналитически граф можно описать с помощью структурной матрицы Ас (матрицы соединений, инциденций), представляющей собой прямоугольную таблицу с числом столбцов, равным числу ветвей, и числом строк, равным числу узлов. Если положительное направление тока в ветви l выбрать от узла k, то элементы структурной матрицы аи определяются из условия:
Анализ матрицы Ас: показывает, что сумма элементов каждого ее столбца равна нулю. Это является следствием зависимости одной из строк, поэтому ее можно исключить из Аc. Узел, строка которого исключается, называют базисным, а матрица Аo, образующаяся при этом, редуцированная.
Кроме матрицы Ас при анализе электрических цепей используется матрица сечений С, представляющая собой таблицу со строками, соответствующими сечениям графа и столбцами — его ветвями. Если за положительное направление принять направление ветви внутрь области, охваченной сечением, то элементы Матрицы сечений сы определяются следующим образом:
Матрицей контуров В называют таблицу, с числом строк равным числу независимых контуров, и числом столбцов равным числу ветвей. Элементы матрицы контуров определяются по правилу
Число независимых контуров определяется числом хорд графа , (1.15).
studfiles.net










Поделиться с друзьями: