Схемаэлектрической цепиэто условное графическое изображение цепи. Примером схемы электрической цепи может служить схема системы передачи энергии от генератора1к потребителю3через линию электропередачи2, изображенная на рис.3.13. Основой для расчета электрической цепи служит схема замещения электрической цепи (эквивалентная схема), представляющая схему, состоящую из основных элементов ,,,,и отображающая свойства реальной цепи. Схема замещения реальной цепи, представленной на рисунке 3. 13, может иметь вид, изображенный на рис.3.14. Введем понятия узел, ветвь, контурэлектрической цепи и соответственно ее схемы. Ветвьучасток схемы, в котором в любой момент времени ток имеет одно и то же значение. Ветвь может содержать любое число последовательно соединенных элементов цепи. Последовательное соединение‑ это такое соединение элементов, когда по ним протекает один и тот же ток. Узелместо соединения ветвей. Параллельнымсоединением ветвей называют такое соединение, при котором все ветви присоединяются к одной паре узлов и ко всем этим ветвям приложено одно и то же напряжение. Смешаннымсоединением называют комбинацию последовательных и параллельных соединений. Сложные цепи могут не сводиться к перечисленным типам соединений. Контурэто любой замкнутый путь, проходящий по нескольким ветвям. К каждому узлу в контуре присоединены две ветви. В рассмотренном примере (схема рис.3.14) имеем: число узлов = 3; число ветвей = 5; ветви 1, 3, 5 содержат последовательно соединенные элементы; ветви 1 и 2, а также 4 и 5 соединены параллельно; ветвь 2 соединена параллельно участку, образованному ветвями 3, 4 и 5; ветвь 1 соединена последовательно с участком, образованным ветвями 2, 3, 4 и 5; ветви 1, 4, 5 не образуют какого либо из рассмотренных типов соединений; ветви 2, 3, 5 образуют контур (2,3,5), можно также выделить следующие контуры : (1,2), (2,3,4), (4,5), (1,3,4), (1,3,5). Введем основные топологические понятия схемы электрической цепи. Графсхемыэто такое графическое (топологическое) представление схемы, при котором ветви схемы изображаются отрезками (или дугами), а узлыточками. Отрезки называют ветвями графа, а точкиузламиграфа. Такое представление является наглядным изображением взаимных соединений ветвей схемы. Условимся ветвь с идеальным источником тока не включать в граф схемы, так как внутренняя проводимость идеального источника тока равна нулю и соответственно сопротивление таких ветвей бесконечно велико. Для схемы, изображенной на рисунке 3.14, граф имеет вид (рис.3.15а) Если условные положительные направления токов в электрической схеме перенести на граф, то получим направленныйграф (рис.3.15б). На рисунке 3.16 представлены схема электрической цепи и ее направленный граф При описании графа цепи полезно использовать понятие дерева графа. Деревографаэтосвязаннаячасть графа, включающая все узлы и не имеющая ни одного контура. Дерево графа с узлами содержит () ветвь. Один и тот же граф может иметь различные деревья. Например, для графа, изображенного на рис.3.16, деревья могут принимать следующий вид Связиграфаэто ветви, дополняющие дерево до исходного графа. Число связей, гдечисло ветвей,число узлов. studfiles.net 1)Электрическая
цепь: 2) Элемент электричес- кой цепи: Элементы электрической
цепи – устройство или прибор,
выполняющий определенные функции. Все элементы электрической цепи
принципиально делятся на источники и потребители: 3) монтажная схема электрической
цепи. Монтажная схема -изображает элементы цепи и соединительные провода. 4) принципиальная схема электрической
цепи. Принципиальная
схема – на ней показываются условные графические изображения элементов и
их соединений. 5) схема
замещения электрической цепи. Схема замещения – расчетная модель электрической цепи, на которой
элементы замещаются идеализи -рованными элементами без вспомогательных
элементов, не влияющих на результаты расчетов. 6)Иисточники эц: В
качестве источников питания применяются эл. генераторы, аккумуляторы и
первичные элементы. 7) Приемники эц: К приёмникам эл. энергии относятся электродвигате ли, лампы накаливания, нагревательные устройст ва и тд. 8)Классификация эц по роду тока: . ПО РОДУ ТОКА: - 1. цепи постоянного тока (ток, не меняющ. во времени), 2. цепи
переменного тока (синусоидально-измененяющийся ток I(t) 9) Линейные эц: Линейные –
ЭЦ сопротивление каждого эл-та кот. не зависит ни от тока, ни от напряжения.
Зависимость напряж. от тока показывается на вольт-амперных хар-ках. I(t) t 10)Нелинейные эц: Нелинейные –
если хотя бы один эл-т в цепи имеет сопрот-е, зависящее или от тока или от
напряж-я. I(t) t 11) Простые
эц: Все элементы соединены последовательно 12)Сложные эц: Сложнее электрические цепи содержат азветвления 13) Идеальный
источник ЭДС: Ид ист ЭДС – источник, напряжение на зажимах которого не зависит
от тока 14)
Идеальный источник тока: Источник энергии, ток через который не зависит от напряжения на
его зажимах 15)
Схемы замещения реальных источников энергии: Графическое
изображение Эл. цепи, составленное из условных обозначений электротехнич.
устройств, наз. принципиальной схемой. Схема замещения эл. цепи является её
количественной моделью. Она состоит из совокупности различных идеализированных
элементов, выбранных так, чтобы можно было с хорошим приближением описать процессы
эл. цепи. Рассмотрим
один из распространённых источников энергии постоянного тока – гальванический
элемент. Между разноимённо заряженными пластинами возникает однородное Эл. поле
с напряженностью Е [В/м], которое препятствует направленному движению ионов в
растворе. Напряжение, при котором накопление зарядов прекращается, служит
количественной мерой сторонней силы. Её называют электродвижущей силой (ЭДС,
ξ). Если к выводам гальванического элемента подключить приёмник,. То в
замкнутой эл. цепи возникнет ток. Заряд каждой из пластин уменьшится и появится
направленное движение ионов в растворе кислоты. Направленное движение ионов
сопровождается их взаимными столкновениями, что создает внутреннее
сопротивление гальванического элемента постоянному току. Т.о., эскизное
изображение которого дано на рис.1, а изображение на принципиальных схемах – на
рис.2, можно представить в виде схемы замещения (рис.3), состоящей из последовательно
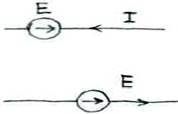
включенных источника ЭДС ξ и резистивного элемента с сопротивлением 16) Закон Ома для участ-ка цепи: Uab = IR => I = Uab/R 17)
закон Ома для участка цепи, содержа -щего источник ЭДС: Uab a I R c E b Uab = Uac + Ucb Uac = IR Ucb = φc - φb = - E φb - φc = E Uab = IR – E I = (Uab + E)/R 18)
Режимы работы источников энергии: Ист. тока и ЭДС м. раб-ть как
в режиме ист. тока так и в режиме потребителей (приемников) эл-ой эн-ии.
Источник ЭДС работает в режиме потреб-ля , если напряжения тока ч/з него и ЭДС
не совпадают. (рис-1 – потребитель, 2-источник): Ист. тока раб. в режиме
потребителя, если напряж. на зажиме, из кот вытекает ток, выше чем, на
зажиме, в котором ток втекает. 19,26) Баланс
мощностей в цепи постоянного тока: Сумме мощностей энергии равна сумме мощностей приёмников энергии ∑ Pист = ∑Pпр Pист = EI Если направление тока и ЭДС через источник тока не совпадает, то
исто -чник потребляет энергию 20)
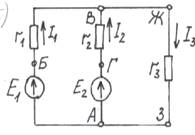
первый закон Кирхгофа Для
узла А можно написать:, I1 + I2
– I3 – I4 – I5
= 0 а в общем виде 21) второй закон Кирхгофа Рассмотрим
источники, работающие в режиме генератора, т.е. аправления токов совпадают с
направ -лениями ЭДС. Одинаковое для них напряжение между точками ВА или, что то
же, между точками ЖЗ определяется по формуле: По первому зак. Кирхгофа составляется Y – 1 урав- нений. Направления токов выбираются произвольно По II-му составляется B – (Y - 1) – T уравнений,
где В – кол. ветвей в цепи Y – кол. узлов в цепи T – кол. ветвей содерж. источник тока. 23)
расчёт цепей постоян -ного тока методом контурных токов Он снован на предположении, что в каждом независимом контуре, в
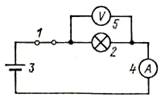
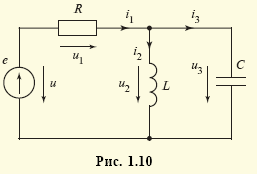
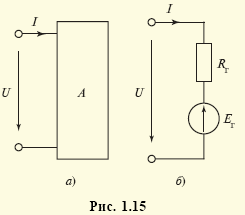
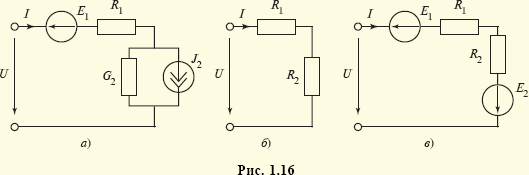
каждой vunivere.ru Основными элементами электрических цепей являются источники электромагнитной энергии (см. § 1.1), элементы передачи (линии электропередачи, линии связи) и преобразования (трансформаторы, различные преобразователи — выпрямители, инверторы и др.) энергии, а также приемники энергии, в которых электромагнитная энергия преобразуется в энергию других видов, например в механическую (электрические двигатели), химическую (аккумуляторы), тепловую (электрические печи) и т.п. Источники энергии принято называть активными элементами, а ту часть цепи, в которой они действуют, — активной подцепью, все остальные элементы — пассивными элементами, а часть цепи, в которой нет активных элементов, — пассивной подцепью. Сложность изучения всего многообразия реальных элементов цепей (линий электропередачи, трансформаторов, генераторов и др.) породила необходимость выделения минимального набора простейших элементов, с помощью комбинаций которых можно описывать эти реальные элементы. К таким элементам относят источники энергии: источник ЭДС (схемное обозначение представлено на рис. 1.6, а), источник тока (рис. 1.6, б), резистор (рис. 1.6, в), конденсатор (рис. 1.6, г) и индуктивная катушка (рис. 1.6, д). Для источника ЭДС (рис. 1.6, а) характерным является равенство напряжения между его выводами значению электродвижущей силы: для источника тока (рис. 1.6, б) — численное равенство тока i элемента значению тока J источника: для резистора (рис. 1.6, в) — линейная связь напряжения и тока: для конденсатора (рис. 1.6, г) — линейная связь тока элемента с производной напряжения: для катушки (рис. 1.6, д) — линейная связь напряжения с производной тока: При этом уравнения (1.1)—(1.5) называют компонентными уравнениями рассматриваемых элементов, параметры R(G), С и L этих элементов — соответственно сопротивлением (проводимостью) резистора, емкостью конденсатора и индуктивностью катушки, а значения тока i(t), напряжения u(t) и ЭДС e(t) в момент времени t соответственно мгновенными значениями i, u, e. Выражение (1.3) носит название закона Ома, а произведение мгновенных значений напряжения и тока p = ui, называемое мгновенной мощностью, для резистора равно р = ui = Ri2 (закон Джоуля—Ленца). Мощность в данном случае определяет количество теплоты, выделяемое резистором в единицу времени. Таким образом, резистор (резистивный элемент) — это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является ом — 1 Ом = 1 В/1 А (проводимости — сименс — 1 См = 1 А/1 В), мгновенной мощности — ватт — 1 Вт = 1 В · 1 А. Сопротивлением R можно охарактеризовать любой проводник длиной l и сечением S (рис. 1.7), причем если ток распределен по сечению проводника равномерно, то Конденсатор (емкостной элемент) запасает энергию электрического поля Wэ = Cu2/2, его мгновенная мощность Катушка индуктивности (индуктивный элемент) запасает энергию магнитного поля Wм = Li2/2, ее мгновенная мощность Ток i в этом случае создает магнитное поле, направление индукции В которого показано линиями со стрелками. Интегрально его можно охарактеризовать для каждого витка потоком Таким образом, любая часть реальной электрической цепи обладает всеми перечисленными параметрами — R, L, С, а названные выше — резистор, конденсатор, катушка — суть элементы, в которых соответственно сопротивление, емкость и индуктивность являются основными параметрами, другими же параметрами обычно пренебрегают. Электрическую цепь удобно изображать в виде чертежа, называемого схемой электрической цепи. Такая схема составляется из условных обозначений элементов цепи (см. рис. 1.6) и показывает их соединение. При этом последовательность элементов, имеющих один и тот же ток, называют ветвью, место соединения ветвей — узлом, замкнутый путь, проходящий по нескольким элементам, называют контуром. Для любого узла справедлив первый закон Кирхгофа: алгебраическая сумма мгновенных значений токов в ветвях, соединенных с данным узлом, равна нулю: ∑i = 0. Для любого контура справедлив второй закон Кирхгофа: алгебраическая сумма напряжений на всех элементах любого замкнутого контура равна нулю: ∑u = 0. Если число ветвей цепи равно В, узлов У, то число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно У – 1, по второму — В – У + 1 . Дополнив В уравнений, составленных по первому и второму законам Кирхгофа (У – 1 + В – У + 1 = В), компонентными уравнениями элементов цепи, можно получить полную систему ее уравнений, позволяющую решить задачу анализа: по заданной схеме и значениям параметров элементов рассчитать неизвестные токи и напряжения ветвей цепи. Пример 1.1. Для цепи, изображенной на рис. 1.10, имеем: число узлов равно двум, число ветвей — трем, число элементов — четырем. Тогда согласно первому закону Кирхгофа имеем согласно второму закону Кирхгофа: Компонентные уравнения имеют вид Полная система уравнений электрической цепи (1.6)—(1.8) позволяет по известным параметрам е = e(t), R, L, С найти все токи и напряжения активного (источник ЭДС) и трех пассивных (резистор, катушка индуктивности, конденсатор) элементов цепи, т.е. решить задачу анализа цепи при условии, что заданы также начальные значения (т.е. значения переменных в момент времени, равный нулю) тока катушки i2(0) = i02 и напряжения конденсатора u3(0) = u03, которые необходимы для решения алгебродифференциальных уравнений (1.6)—(1.8). В общем случае для решения задачи анализа сложной электрической цепи (т.е. задачи определения всех неизвестных токов и напряжений ее элементов при известной схеме и параметрах — сопротивлениях, емкостях, индуктивностях, ЭДС и токах источников тока) полную систему уравнений составляют редко. Более эффективными оказываются иные подходы, основанные, например, на различных преобразованиях схем (см. ниже) или использовании более простых — канонических уравнений, связывающих лишь часть из неизвестных переменных. Такие канонические уравнения оказывается возможным составлять относительно переменных, определяющих энергетическое состояние цепи, т.е. запасы ее электрической и магнитной энергии. Поэтому подобные канонические уравнения называют уравнениями состояния электрической цепи, а переменные, относительно которых они составляются, — переменными состояния. Из сказанного следует, что переменными состояния для электрических цепей являются токи индуктивных элементов, определяющих запас магнитной энергии, и напряжения емкостных элементов, определяющих запас электрической энергии. Пример 1.2. Выразив ток i3 из уравнения (1.6) i3 = i1 – i2 и воспользовавшись компонентными уравнениями (1.8) u1 = Ri1, u = е, из системы уравнений (1.7) найдем Следовательно, Тогда из компонентных уравнений (1.8) Полученная в примере 1.2 каноническая форма дифференциального уравнения удобна для аналитического либо численного (с помощью стандартных пакетов программ интегрирования дифференциальных уравнений) решения. Под решением здесь понимаются определенные зависимости тока индуктивного элемента i2 = i2(t) и напряжения емкостного элемента u3(t) от времени. Располагая такими зависимостями и уравнениями (1.6), (1.8), аналогичные зависимости от времени для остальных переменных i1(t), i3(t), u1(t), u2(t) находят уже с помощью одних алгебраических операций. Для электрической цепи закон сохранения энергии записывается в виде равенства суммы генерируемых источниками мгновенных мощностей сумме мгновенных мощностей остальных элементов Пример 1.3. Согласно теореме Телледжена для схемы рис. 1.10 имеем ei1 = u1i1 + u2i2 + u3i3, где е = u. Электрические цепи принято классифицировать по типу параметров элементов и типу электромагнитных процессов в них. Так, говорят о линейных цепях, если параметры элементов е = e(t), J = J(t), R, L, С не зависят от интенсивностей электромагнитных процессов (т.е. от токов и напряжений этих элементов). Подобные цепи описываются линейными системами уравнений, решение которых может быть достигнуто с использованием принципа суперпозиции (наложения), когда можно рассматривать вклад параметра е или J каждого источника энергии в решение независимо от вклада в него других источников. Линейные цепи называют стационарными, если параметры R, L, С их элементов — константы, и параметрическими, если эти параметры известные функции времени R = R(t), L = L(t), С = C(t). Если же параметры е, J, R, L, С зависят от интенсивности процессов, то сами элементы и цепи, их содержащие, называют нелинейными элементами и цепями. Уравнения таких цепей нелинейны, и поиск их решения с гарантированной точностью представляет собой весьма сложную задачу. Различают также элементы и цепи с сосредоточенными и распределенными параметрами. О сосредоточенных параметрах R, L, С говорят в том случае, когда они сосредоточены (локализованы) на определенном участке. Если же приходится учитывать геометрическую протяженность этого участка, то эти параметры считаются распределенными. Параметры R, L, С в этом случае характеризуют единицами Ом/м, Гн/м, Ф/м. Цепи с распределенными параметрами описываются уравнениями в частных производных, решение которых весьма трудоемко. Следует отметить, что допущение о линейности и сосредоточенности параметров справедливо лишь для определенных диапазонов интенсивностей процессов, т.е. является условным, и в этом смысле говорят о границах абстракций в теории электрических цепей. По типу электромагнитных процессов цепи подразделяют на цепи постоянных токов (если токи и напряжения всех элементов цепей не изменяются во времени), цепи переменных токов (если токи и напряжения всех элементов цепей изменяются во времени) и, в частности, цепи синусоидальных токов (если эти токи и напряжения цепей изменяются во времени по синусоидальным законам). Следует заметить, что в частных случаях, когда процессы в цепях описываются функциями одного вида, например постоянными или синусоидальными функциями, расчет цепей резко упрощается. Существует масса приемов и методов расчета таких цепей. Ознакомимся с некоторыми из них. Но прежде всего обратим внимание на то, что в схемах замещения цепей постоянных токов отсутствуют емкостные и индуктивные элементы. В самом деле, из допущения о постоянстве тока из компонентного уравнения (1.5) индуктивного элемента (см. рис. 1.6, д) следует, что напряжение его будет равным нулю, т.е. сам индуктивный элемент в схеме замещения цепи на постоянном токе представляет собой идеальный проводник с нулевым сопротивлением — так называемую «закоротку». Из допущения о постоянстве напряжения для емкостного элемента (см. рис. 1.6, г) из компонентного уравнения (1.4) следует, что его ток в этом случае будет равен нулю, а сам емкостной элемент представляет собой «разрыв» ветви цепи. Полученная резистивная цепь описывается уже не дифференциальными, а чисто алгебраическими уравнениями, решение которых не представляет особой сложности. Пример 1.4. Схема рис. 1.10 для случая, когда ЭДС источника e(t), токи i1(t), i2(t), i3(t) и напряжения u1(t), u2(t), u3(t) постоянны, т.е. е = Е, i1 = I1, i2 = I2, i3 = I3, u1 = U1, u2 = U2, u3 = U3, может быть представлена в виде рис. 1.11. При этом I3 = 0, U2 = 0, а токи I1 = I2 и напряжение U3 находятся из уравнений второго закона Кирхгофа U1 + U2 = Е, U3 = U2, где U1 = I1R. Окончательно имеем I1 = I2 = E/R. При расчетах резистивных цепей можно пользоваться следующими преобразованиями, основанными на использовании компонентных уравнений и уравнений Кирхгофа: последовательно соединенные резисторы с сопротивлениями R1 и R2 (рис. 1.12, а) можно заменить одним эквивалентным резистивным элементом с сопротивлением Rэ = R1 + R2 (рис. 1.12, б), не изменив при этом общего тока I и на пряжения U ветви; параллельно соединенные резисторы с проводимостями G1 = l/R1 и G2 = l/R2 (рис. 1.13, а) можно заменить одним эквивалентным резистивным элементом с проводимостью Gэ = G1 + G2 (с сопротивлением источник ЭДС Е с внутренним сопротивлением Rвн (рис. 1.14, а) можно заменить источником тока J с внутренней проводимостью Gвн (рис. 1.14, б) при условии J = E/Rвн, Gвн = 1/Rвн; аналогично источник тока J с внутренней проводимостью Gвн (рис. 1.14, б) можно заменить источником ЭДС Е = J/Gвн с внутренним сопротивлением Rвн = 1/Gвн (рис. 1.14, а), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи. Используя подобные методы преобразования схемы цепи, можно существенно упростить ее схему и соответственно расчет токов и напряжений. Наряду с подобными методами преобразования при расчете цепей постоянных токов или в более общем случае любых чисто резистивных цепей используют и специальные методы упрощения их схем. Наиболее известным из них является метод эквивалентного генератора. Суть его сводится к эквивалентной замене любого активного (т.е. содержащего источники энергии) двухполюсника А (т.е. подцепи, присоединенной к остальной части цепи двумя узлами) (рис. 1.15, а) источником ЭДС Ег, называемой ЭДС эквивалентного генератора с последовательно включенным внутренним сопротивлением Rг (рис. 1.15, 6). При этом значение Ег равно напряжению так называемого «холостого хода», т.е. напряжению U на разомкнутых зажимах двухполюсника. Это напряжение можно непосредственно измерить, если цепь существует в виде реального устройства, или рассчитать, если она задана в виде схемы с известными параметрами. Внутреннее сопротивление такого генератора определяется как сопротивление двухполюсника А с замкнутыми источниками ЭДС и разорванными ветвями с источниками тока. Пример 1.5. Определим параметры эквивалентного генератора активного двухполюсника (рис. 1.16, а). «Закоротив» источник ЭДС Е1 и «разорвав» ветвь с источником тока J2, получим схему рис. 1.16, б, эквивалентное сопротивление которой R1 + 1/G2 как раз и будет равно внутреннему сопротивлению эквивалентного генератора, т.е. Rг = R1 + 1/G2. Для определения ЭДС этого генератора заменим источник тока J2 с проводимостью G2 эквивалентной ЭДС Е2 = J2/G2 с сопротивлением R2 = 1/G2 (см. выше). Напряжение холостого хода (I = 0) для полученной схемы (рис. 1.16, в) будет, очевидно, равно U = E1 – E2. Таким образом схему, изображенную на рис. 1.16, а, можно заменить эквивалентным генератором, изображенным на рис. 1.15, б, с параметрами Ег = E1 – J2/G2, Rг = R1 + 1/G2. Заменяя отдельные подцепи, соединенные с остальной частью цепи только двумя узлами, подобными эквивалентными генераторами, можно существенно упростить расчет цепи. В общем случае методика расчета сложной электрической цепи, основанная на замене ее отдельных подцепей более простыми подцепями (типа эквивалентных генераторов для двухполюсников), называется диакоптикой электрических цепей. Введенная в теорию электрических цепей Г. Кроном диакоптика является в настоящее время одной из наиболее востребованных практикой методикой их расчета. Электрические цепи: элементы, схемы, законы, классификация. Схемы электрической цепи
Схемы электрических цепей
Топологические понятия схемы электрической цепи
Электрическая цепь и ее элементы. Принципиальная схема электрической цепи. Схема замещения электрической цепи
 Совокупность устройств для получения в них эл. тока наз. электрической
цепью. В основном цепь состоит из источников питания, приёмников энергии, или
потребителей, и проводов для передачи эл. энергии.
Совокупность устройств для получения в них эл. тока наз. электрической
цепью. В основном цепь состоит из источников питания, приёмников энергии, или
потребителей, и проводов для передачи эл. энергии. 
 t
t
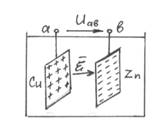
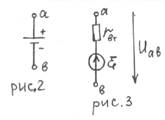
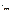 . Равным внутреннему сопротивлению
гальванического элемента. Стрелка ЭДС указывает направление движения положительных
зарядов внутри источника под действием сторонних сил. Схема замещения рис.3
применяется и для любых других источников эл. энергии постоянного тока.
. Равным внутреннему сопротивлению
гальванического элемента. Стрелка ЭДС указывает направление движения положительных
зарядов внутри источника под действием сторонних сил. Схема замещения рис.3
применяется и для любых других источников эл. энергии постоянного тока.





 Pпр = I2 R
Pпр = I2 R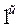 закон Кирхгофа: сумма токов,
направленных к узлу, равна сумме токов, направленных от него.
закон Кирхгофа: сумма токов,
направленных к узлу, равна сумме токов, направленных от него.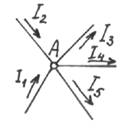
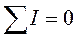 ,т.е.алгебраичеc-кая
сумма токов в узле равна нулю. При этом токи, направленные от узла, считаются
отрицательными.
,т.е.алгебраичеc-кая
сумма токов в узле равна нулю. При этом токи, направленные от узла, считаются
отрицательными. 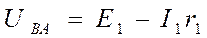
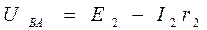 Тогда
для замкнутого контура АБВГДА спра -ведливо уравнение
Тогда
для замкнутого контура АБВГДА спра -ведливо уравнение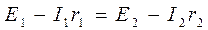 откуда
откуда 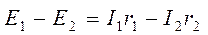 или
в обшей форме
или
в обшей форме  .
. 22) расчёт цепей посто- янного тока путём непосредственного
применения законов Кирхгофа.
22) расчёт цепей посто- янного тока путём непосредственного
применения законов Кирхгофа.Электрические цепи: элементы, схемы, законы, классификация

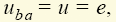
(1.1)
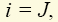
(1.2)
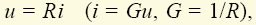
(1.3)

(1.4)
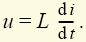
(1.5)
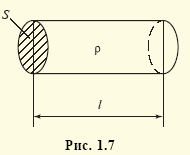
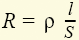 , где ρ — удельное электрическое сопротивление, характеризующее свойства материала проводника. Единицей удельного электрического сопротивления является ом х метр (Ом · м). Поэтому в схеме замещения (см. ниже) электрической цепи резистивные элементы отражают не только собственно резисторы, но и сопротивления проводов линий электропередач, сопротивления проводников, из которых выполнены обмотки трансформаторов, электрических машин и т.п.
, где ρ — удельное электрическое сопротивление, характеризующее свойства материала проводника. Единицей удельного электрического сопротивления является ом х метр (Ом · м). Поэтому в схеме замещения (см. ниже) электрической цепи резистивные элементы отражают не только собственно резисторы, но и сопротивления проводов линий электропередач, сопротивления проводников, из которых выполнены обмотки трансформаторов, электрических машин и т.п.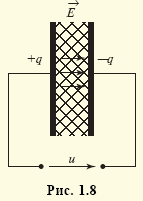
 — характеризует скорость изменения этой энергии во времени. Конденсатор выполняется в виде двух металлических пластин, разделенных слоем диэлектрика (рис. 1.8). Собственно емкость, для использования которой и предназначен этот элемент, представляет собой отношение двух равных по значению, но противоположных по знаку зарядов пластин, разнесенных в пространстве (рис. 1.8), к напряжению этого элемента С = q/u. Единицей емкости является фарад — 1 Ф = 1 Кл/1 В. Емкостью обладает не только конденсатор, но и пары проводов электропередач, емкостью характеризуется связь каждого из этих проводов с землей и т.д. При составлении схемы замещения реальной цепи необходимо отражать подобные связи емкостными элементами, входящими в схему наравне с конденсаторами.
— характеризует скорость изменения этой энергии во времени. Конденсатор выполняется в виде двух металлических пластин, разделенных слоем диэлектрика (рис. 1.8). Собственно емкость, для использования которой и предназначен этот элемент, представляет собой отношение двух равных по значению, но противоположных по знаку зарядов пластин, разнесенных в пространстве (рис. 1.8), к напряжению этого элемента С = q/u. Единицей емкости является фарад — 1 Ф = 1 Кл/1 В. Емкостью обладает не только конденсатор, но и пары проводов электропередач, емкостью характеризуется связь каждого из этих проводов с землей и т.д. При составлении схемы замещения реальной цепи необходимо отражать подобные связи емкостными элементами, входящими в схему наравне с конденсаторами.
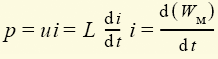 характеризует скорость изменения этой энергии во времени. Конструктивно такой элемент часто выполняется из проводника в виде спирали (рис. 1.9).
характеризует скорость изменения этой энергии во времени. Конструктивно такой элемент часто выполняется из проводника в виде спирали (рис. 1.9). через поверхность S. Произведение этого потока на число витков w катушки называют потокосцеплением ψ = Фw. Индуктивность характеризует связь между этим потокосцеплением и вызывающим его током ψ = Li. Единицей магнитного потока является тесла — 1 Тл = 1 Вб · 1 м2, индуктивности — генри — 1 Гн = 1 Тл/1 А. Таким образом, индуктивная катушка — это элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо собственно катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередач, что необходимо отражать в схемах замещения соответствующих цепей.
через поверхность S. Произведение этого потока на число витков w катушки называют потокосцеплением ψ = Фw. Индуктивность характеризует связь между этим потокосцеплением и вызывающим его током ψ = Li. Единицей магнитного потока является тесла — 1 Тл = 1 Вб · 1 м2, индуктивности — генри — 1 Гн = 1 Тл/1 А. Таким образом, индуктивная катушка — это элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо собственно катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередач, что необходимо отражать в схемах замещения соответствующих цепей. 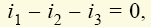
(1.6)

(1.7)
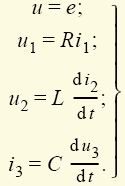
(1.8)
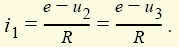
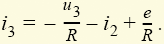
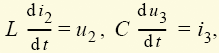 уравнения u2 = u3 (1.7) и полученного уравнения для i3 находим уравнения состояния электрической цепи, изображенной на рис. 1.10:
уравнения u2 = u3 (1.7) и полученного уравнения для i3 находим уравнения состояния электрической цепи, изображенной на рис. 1.10: 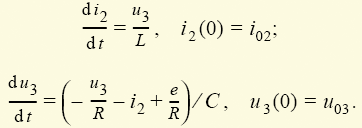
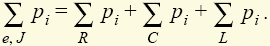 Это выражение, представляющее собой запись теоремы Телледжена, показывает, что энергия источников расходуется на теплоту, выделяемую резисторами, и перераспределение запасов электрической и магнитной энергии, запасенных конденсаторами и катушками. В этой связи говорят о балансе мгновенных мощностей цепи.
Это выражение, представляющее собой запись теоремы Телледжена, показывает, что энергия источников расходуется на теплоту, выделяемую резисторами, и перераспределение запасов электрической и магнитной энергии, запасенных конденсаторами и катушками. В этой связи говорят о балансе мгновенных мощностей цепи.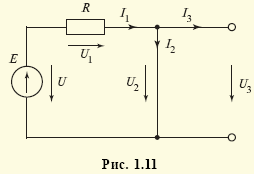
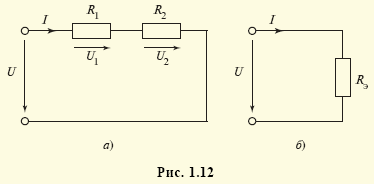
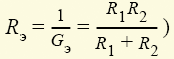 (рис. 1.13, 6), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи;
(рис. 1.13, 6), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи;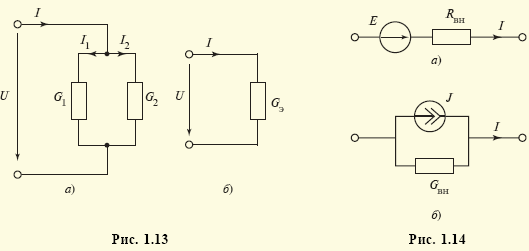
Похожие статьи:
poznayka.org
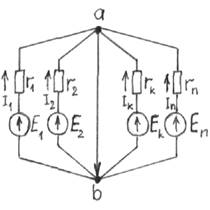
Расчет электрических цепей производится с применением различных методов, с помощью которых производятся вычисления. Всем известно, что одну и ту же задачу вполне можно решить с помощью нескольких способов. В конечном итоге, при одном и том же результате, сложность расчетов всегда будет значительно различаться. Для того, чтобы выбрать корректный метод расчета необходимо определить ее класс. Все цепи разделяются на два основных класса – простой и сложный. Классификация электрических цепейПростыми считают цепи, в состав которых включен всего один источник электроэнергии (Е), как это видно на схеме слева. К простым относят также и с двумя источниками электроэнергии (Е1 и Е2), которые расположены совместно на общей ветви эл. цепи. Это очень хорошо просматривается на правой схеме. Назначение электрической цепиЭлектрическая цепь создается для того, чтобы обеспечить нормальную работу какого-либо электротехнического устройства. То есть, главной задачей является передача этому устройству электрической энергии и обеспечение требуемого режима работы. Таким образом, она представляет собой комплекс различных устройств и приборов, которые и образуют путь прохождения электротока. Для того, чтобы правильно проанализировать и произвести расчет электрических цепей, составляются графические схемы, в которых указываются элементы в виде условных обозначений и все виды их соединений. Схема, приведенная выше, отображает самую простую цепь, обеспечивающую работу аппаратуры освещения. Здесь электроэнергия, поступает из источника (Е), имеющего внутреннее сопротивление (r0). С помощью реостата (R) и вспомогательных элементов, электроэнергия передается к потребителям, в данном случае – это лампочки EL1и EL2. Составные части электрических цепейВсе приборы и устройства, которые составляют электрическую цепь, условно разделяются на три основные группы:
Все эти элементы входят в общий электромагнитный процесс. Методы расчета электрических цепей |
electric-220.ru
Схемы электрических цепей и их элементы.
Тема 1. Введение
Электротехника - техническая дисциплина, которая занимается анализом и практическим использованием для нужд промышленного производства и быта всех физических явлений, связанных с электрическими и магнитными полями. Область практического применения электротехники имеет четыре связанные друг с другом направления :
1. Получение электрической энергии.
2. Передача энергии на расстояние.
3. Преобразование электромагнитной энергии.
4. Использование электроэнергии.
Научно-технический прогресс происходит при все более широком использовании электрической энергии во всех отраслях отечественной промышленности. Поэтому электротехническая подготовка инженеров не электротехнических специальностей должна предусматривать достаточно подробное изучение вопросов теории и практики использования различных электроустановок. Инженер любой специальности должен знать устройство, принцип действия, характеристики и эксплуатационные возможности электрических цепей, электрических машин, различных аппаратов и другого электрооборудования, способы регулирования и управления ими.
История развития электротехники как науки связана с важнейшими исследованиями и открытиями. Это исследования атмосферного электричества, появление источников непрерывного электрического тока - гальванических элементов (1799 г.), открытие электрической дуги (1802 г.) и возможность ее использования для плавки металлов и освещения, открытие закона о направлении индуцированного тока (1832 г.) и принципа обратимости электрических машин, в 1834 г. впервые осуществлен электропривод судна, открытие закона теплового действия тока - закона Джоуля - Ленца (1844 г.), в 1876 г. положено начало практическому применению электрического освещения с изобретением электрической свечи, в 1889-1891 гг. созданы трехфазный трансформатор и асинхронный двигатель.
В настоящее время отечественная электроэнергетика занимает передовые позиции в мире по созданию мощных ГЭС и каскадов электростанций, производству мощных гидрогенераторов, высоким темпам теплофикации, строительству высоковольтных линий электропередач и мощных объединенных энергосистем, высокому техническому уровню электросетевого хозяйства.
В современных производственных машинах с помощью электротехнической и электронной аппаратуры осуществляется управление ее механизмами, автоматизация их работы, контроль за ведением производственного процесса, обеспечивается безопасность обслуживания и т.д. Все шире используется в технологических установках электрическая энергия, например, для нагрева изделий, плавления металлов, сварки.
Основной задачей данного курса является получение основных сведений и формирование знаний, умений и навыков по электротехнике, электронным устройствам и электроприводу.
Тема 2. Линейные электрические цепи постоянного тока.
Основные понятия и определения.
Электрической цепью называется совокупность источников и потребителей электрической энергии, соединенных друг с другом с помощью проводников.
Электрический ток - направленное движение заряженных частиц (электронов или ионов ).
Постоянный ток - ток, неизменный по величине и направлению.
Ветвью называется участок цепи между двумя соседними узлами, содержащий последовательное соединение элементов.
Точка, где соединяются три и более ветвей называется узлом.
Любой замкнутый путь, проходящий по ветвям данной цепи, называется контуром.
Основными параметрами, характеризующими электрические цепи постоянного тока, являются: I(А)- сила тока - количество электричества, проходящего через поперечное сечение проводника за единицу времени, U(В) - напряжение на некотором участке электрической цепи, равное разности потенциалов на концах этого участка, R(Ом) - сопротивление, Р(Вт)- мощность. Все обозначения основных физических величин предусмотрены государственным стандартом. Единицы измерения диктуются международной системой единиц.
Схемы электрических цепей и их элементы.
Графическое изображение электрической цепи и ее элементов называется электрической схемой (рис. 1)
| На любую машину, в состав которой входят электрические устройства, кроме конструкторских чертежей имеется электродокументация, состоящая из различных электрических схем. Электрические функциональные схемы раскрывают принцип действия устройства. Существуют электромонтажные схемы, в которых раскрывается монтаж (соединение) электрических элементов цепи. Электрические принципиальные схемы раскрывают электрические связи всех отдельных элементов электрической цепи между собой. |
Все схемы вычерчиваются по определенным стандартам- ГОСТам. ГОСТы являются основой технического языка, применяемого в масштабе всей страны.
Кроме основных электрических схем существуют схемы замещения, по которым наиболее удобно составлять математические уравнения, описания электрических и энергетических процессов. Такие схемы являются эквивалентными моделями электрической цепи. Схемы максимально упрощены и по ним удобнее провести анализ отображаемых ими сложных электрических цепей.
Все элементы электрических цепей можно разделить на три группы: источники (активные элементы), потребители и элементы для передачи электроэнергии от источников к потребителю (пассивные элементы).
Источником электрической энергии (генератором) называют устройство, преобразующее в электроэнергию какой-либо другой вид энергии (электромашинный генератор - механическую, гальванический элемент или аккумулятор - химическую, фотоэлектрическая батарея - лучистую и т.п.).Источники делятся на источники напряжения (Е,U=соnst, при изменении и I) и источники тока (I=соnst, при изменении U). Все источники имеют внутреннее сопротивление Rвн, значение которого невелико по сравнению с сопротивлением других элементов электрической цепи .
Приемником электрической энергии (потребителем) называют устройство, преобразующее электроэнергию в какой-либо другой вид энергии (электродвигатель - в механическую, электронагреватель - в тепловую, источник света - в световую (лучистую) и т.п.).
Элементами передачи электроэнергии от источника питания к приемнику служат провода, устройства, обеспечивающие уровень и качество напряжения и др.
Условные обозначения элементов электрической цепи на схеме стандартизованы. Примеры:
Законы Ома и Кирхгофа
Закон Ома в простейшем случае связывает величину тока через сопротивление с величиной этого сопротивления и приложенного к нему напряжения:
Сила тока на некотором участке электрической цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению этого участка.
Закон Ома справедлив для любой ветви (или части ветви) электрической цепи, в таких случаях его называют обобщенным законом Ома. Для ветви, не содержащей ЭДС, закон Ома запишется:
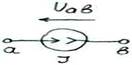
Здесь - потенциалы крайних точек ветви, их разность можно заменить напряжением Uab.
Обобщенный закон Ома для ветви, содержащей ЭДС (т.е. для активной ветви):
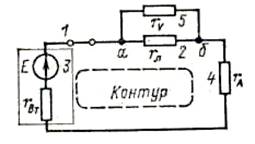
Пример: Записать закон Ома для активной цепи на рис. 2.
Первый закон Кирхгофа
Алгебраическая сумма токов, сходящихся в любом узле электрической цепи равна нулю. При этом токи, текущие к узлу считаются положительными, а от узла - отрицательными. Другая формулировка: сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла.
Первый закон Кирхгофа по сути является законом баланса токов в узлах цепи.
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма падений напряжений на элементах, входящих в контур, равна алгебраической сумме ЭДС.
Второй закон Кирхгофа по сути является законом баланса напряжений в контурах электрических цепей.
Для составления уравнения по 2-му закону Кирхгофа выбирается произвольное направление обхода контура. Тогда, если направление тока в цепи совпадает с направлением обхода, то соответствующее слагаемое берется со знаком "+", а если не совпадает, то со знаком "-". Аналогичное правило расстановки знаков справедливо и для ЭДС.
Пример:
Уравнение по 2-му закону Кирхгофа может быть записано и для контура, имеющего разрыв цепи, однако при этом необходимо в уравнении учитывать напряжение между точками разрыва.
Пример:
pdnr.ru













Поделиться с друзьями: