Катушка индуктивности (дроссель) — катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении, способная накапливать электромагнитную энергию в собственном магнитном поле. Обозначается – L. Внешний вид может быть различным, но если вы её мотаете самостоятельно, то будет выглядеть как-то так: Величина индуктивности измеряется в Генри [Гн]. 1 Генри – очень большая величина, поэтому применяемые в технике катушки индуктивности имеют величины: микрогенри – 10-6 (мкГн) и миллигенри – 10-3 (мГн). Процессы, происходящие в катушке индуктивности (далее — индуктивности) на временном графике при подключении индуктивности к источнику прямоугольного однополярного сигнала, показаны на рисунке. Из рисунка сбоку видно, реакция индуктивности на воздействие электрического тока абсолютно противоположно реакции конденсатора (ёмкости). В момент подачи прямоугольного импульса источника тока (красный), ток индуктивности (фиолетовый) сначала равен нулю и с изменением времени увеличивается по экспоненте – индуктивность накапливает энергию, в начальный момент её внутреннее сопротивление максимально. Напряжение на выводах индуктивности (зелёный) наоборот сначала максимально, но потом по мере накопления энергии уменьшается по экспоненте до нуля. При пропадании входного импульса, так как индуктивность — элемент инерционный, напряжение на выводах индуктивности резко изменив полярность сначала максимально, а ток продолжает течь в том же направлении, уменьшаясь при этом по экспоненте – запасённая в индуктивности энергия иссякает. Напряжение из отрицательной области так же по экспоненте стремится к нулю. Скорость изменения напряжения и тока зависит от значения индуктивности. Чем больше индуктивность, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Если сравнить с конденсатором — полная противоположность. Взаимосвязь тока и напряжения в индуктивности так же описывается законом Ома, с учётом реактивного сопротивления индуктивности. Фактически, мы рассмотрели «четырёхполюсник» состоящий из катушки индуктивности и резистора, который называют интегрирующей цепочкой. Интегрирующая цепочка чаще всего применяется для формирования пилообразных импульсов в любой радио аппаратуре и временной (ударение на «о») задержки прямоугольных импульсов. Чтобы, Вам было понятнее, интегрирующая цепочка и получение пилообразного импульса изображены на следующем рисунке. Для получения последнего, используется наиболее прямолинейный участок интегрированного импульса — его начало, и «обрезается» по времени или по амплитуде (порогу). Для задержки импульсов используют пороговое устройство. По достижении амплитуды сигнала прошедшего через интегрирующую цепочку определённого значения (порога), пороговое устройство пропускает входной сигнал на выход. После чего, сигнал усиливается усилителем до необходимой величины. В целях уменьшения размеров (исключения громоздкости), схемы формирования пилообразных импульсов, и схемы задержки импульсов эффективнее делать на интегрирующей цепочке состоящей из резистора и конденсатора. Кроме функции преобразования прямоугольных импульсов, интегрирующая цепочка может применяться в качестве фильтра низких частот (ФНЧ). Индуктивность – инертный элемент. Если к дросселю с большим значением индуктивности приложить переменное напряжение высокой частоты, в силу своей инертности, индуктивность будет не способной пропустить через себя ток, ведь индуктивности сначала надо будет запастись энергией в собственном сердечнике, а потом отдавать эту энергию. Свойство индуктивности сопротивляться переменному электрическому току называют реактивным сопротивлением индуктивности, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление индуктивности обозначается XL или ZL и измеряется в Омах. Реактивное сопротивление индуктивности связано с частотой тока выражением: Из формулы видно, что реактивное сопротивление индуктивности прямо пропорционально частоте. Другими словами, чем выше частота, тем больше реактивное сопротивление индуктивности. Теперь представьте, что интегрирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает индуктивность. А мы из формулы теперь знаем, что индуктивность легко пропускает низкие частоты – его сопротивление минимально и плохо пропускает высокие частоты – его сопротивление максимально. Не изменяя текста повторюсь: В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке. То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2. Зная, как рассчитывается делитель напряжения и реактивное сопротивление индуктивности на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр низкой частоты на катушке индуктивности (дросселе) и резисторе. Если в интегрирующей цепочке поменять местами индуктивность и резистор, то мы получим – дифференцирующую цепочку. Все процессы в дифференцирующей цепочке происходят точно так же, как и в интегрирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для дифференцирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а катушка индуктивности. Как описывалось в статье про конденсатор: если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1. Cледует добавить, частотные фильтры, выполненные на катушках индуктивности и резисторах, так же, как и на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез, имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом в следующей статье. Наверняка прочитав данную статью, грамотный читатель подумает: «Хм, теория это конечно хорошо, но как измерить руками значение индуктивности на практике?». Однажды этим повросом задался и я, и собрал простую схему для проверки индуктивностей. Чтобы показать всё в работе, было решено записать видео, где всё наглядно и доступно объяснить. Видео доступно на канале сайта на YouTube и на данной странице. Принцип работы там прост: как в теоретической части, на индуктиность подаются прямоугольные импульсы и измеряется сила тока протекающую через схему. Из данных параметров рассчитывается значение индуктивности. meanders.ru Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля. Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком. Это понятно из формулы: Предположим, что ток iL изменился скачком, то есть: А значит, что и напряжение в данном случае будет бесконечно велико: Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности. На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности - “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности. Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается. Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе. Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума. Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R = 10 Ом, L = 0,1 Гн. Скачать файл Multisim 13.0 Рассчитаем время, за которое ток в цепи достигает установившегося значения: Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”. Внутреннее активное сопротивление катушки индуктивности, принято равным нулю. electroandi.ru Доброго времени суток, сегодня мы вам расскажем, что такое индуктивность и как устроена катушка индуктивности. От слова катушка всем приходит на мысль катушка ниток, лески, схожая ситуация и здесь, наматывается изоляционный провод тесно намотанный друг на друга по которому идёт ток. Давайте, все же начнём с термина из википедии: Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как странно это не звучит, но любая катушка индуктивности имеет свою индукцию. Индуктивность катушки измеряется в единицах Генри (Гн), обозначается буковкой L и измеряется LC - метром. Так, что же такое индуктивность? Давайте начнём с начала, если через провод пустить электрический ток, то вокруг создаётся магнитное поле, ниже на картинке приведён пример. На рисунке В - магнитное поле , I - сила тока. Если взять провод и намотать например на карандаш, вы получите спираль, и если подключить её к электрической цепи, затем пропустить по нему ток, то на рисунке ниже мы увидим какие потоки выйдут. Говоря простым языком, чем больше потоков магнитного поля пересекут площадь этого соленоида, тем больше получается магнитный поток (Ф). Потому что по всей конструкции протекает электрический ток. Выходит, что в этот момент он обладает какой-то Силой тока (I). А коэффициент между магнитным потоком и силой тока называется индуктивностью, и вычисляется ниже по формуле. Индуктивность - это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. При увеличении тока на катушке, магнитное поле возрастает, при уменьшении убывает. У катушке индуктивности присутствует особое свойство. Если на катушку подать постоянное напряжение, то в ней возникает противоположное напряжение протекающего в электрической цепи, но этот процесс длится мгновение и исчезает. Такое противоположное напряжение назвали электродвижущей силой самоиндукции, то есть ЭДС. Прочитав нашу статью, что такое ЭДС вы будете знать, что ЭДС зависит от индуктивности катушки. Выходит, что при подачи напряжения на катушку, сила тока изменяет свою величину от 0 до некоторого значения. Тогда напряжение, также меняет свое значение от ноля и до установившегося значения, согласно Закону Ома. Второе свойство катушки индуктивности мы увидим когда разомкнём цепь и тогда ЭДС самоиндукции будет приплюсовываться к напряжению, которое мы подали на катушку. Следовательно и ток будет в самом начале больше, а потом тихонько спадет до нуля. Время спада силы тока также зависит от индуктивности катушки. Сделаем вывод о работе катушки индуктивности. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока резко возрастет в катушке и плавно убавиться до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может. Это в электронике называют первым законом коммутации. Катушка индуктивности делится на два типа, с сердечником и без. Катушка без сердечника это проволока намотанная в спираль. Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллиГенри. В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра. Ниже можно рассмотреть катушку с сердечником. Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но есть одно различие: у них имеется только одна первичная обмотка, которую можно увидеть ниже. Витки катушки, разделённые слоем изоляции, образуют элементарный конденсатор. В многослойных катушках ёмкость возникает между отдельными слоями. Таки образом, катушка индуктивности обладает не только индуктивностью, но и собственной ёмкостью. В большинстве случаев собственная ёмкость катушки индуктивности является вредной, и от неё стремятся избавиться. Для этого катушки индуктивности выполняют со специальными формами каркаса, а обмотки катушки также выполняют специальными способами. Собственная ёмкость катушки также увеличивается, если её намотка выполнена рядами виток к витку. Если вы хотите получать интересные статьи и последние новости электроники, подписывайтесь на рассылку справа. РЕКОМЕНДУЕМ Просмотров: 11285 | Комментариев: 0 | Дата: 17.12.2014 proelektrik.ucoz.ruКатушка индуктивности в цепи постоянного тока. Напряжение на катушке индуктивности формула
Катушка индуктивности (дроссель) | Meanders.ru
Определение и теория катушек индуктивности
Способ измерения индуктивностей
Катушка индуктивности в цепи постоянного тока








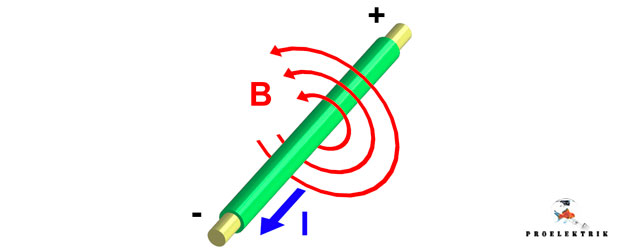
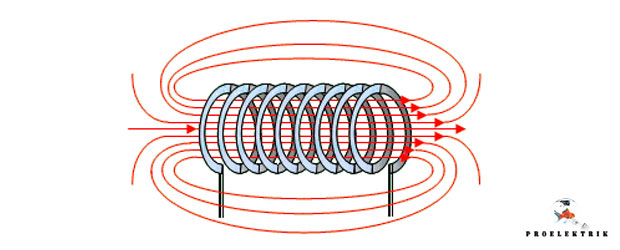
Что такое индуктивность и катушка индуктивности

Что такое катушка индуктивности
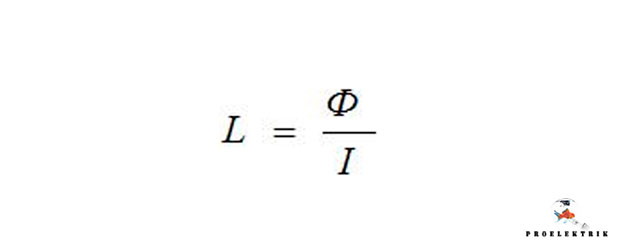
Что такое индуктивность
Какие виды катушек индуктивности бывают


Ёмкость катушки индуктивности
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''










Поделиться с друзьями: