Одним из разделов физики, лежащих в основе умения, посвященного процессам, связанным с электричеством, является электростатика. Она постигает взаимодействие стационарных электрических зарядов. Следственно одной из нормальных задач, которую может понадобиться решить школьникам и студентам младших курсов ВУЗ-ов, является нахождение напряжения между пластинами конденсатора на основании умения разных параметров. Вам понадобится 1. Обнаружьте напряжение между пластинами конденсатора, если знаменита нынешняя величина собранной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C?U?)/2, где C — емкость, а U — напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=?(2?W/C). 2. Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (числа электричества) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q?U/2 (где q — заряд). Следственно, зная энергию и заряд конденсатора, дозволено вычислить напряжение между его пластинами по формуле: U=2?W/q. 3. От того что заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C?U), то, зная заряд и емкость, дозволено обнаружить и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C. 4. Для приобретения значения напряжения на конденсаторе с знаменитыми геометрическими и физическими параметрами, вначале рассчитайте его емкость. Для простого плоского конденсатора, состоящего из 2-х проводящих пластин, поделенных диэлектриком, расстояние между которыми пренебрежимо немного по сопоставлению с их размерами, емкость может быть вычислена по формуле: C=(???0?S)/d. Тут d — расстояние между пластинами, а S — их площадь. Значение ?0 — электрическая непрерывная (константа, равная 8,8542•10^-12 Ф/м), ? — относительная диэлектрическая проницаемость пространства между пластинами (ее дозволено узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из способов, приведенных в шагах 1-3. Для того дабы знать, дозволено ли применять в том либо другом месте схемы конденсатор, следует определить его емкость . Метод нахождения этого параметра зависит от того, каким образом он обозначен на конденсаторе и обозначен ли вообще. Вам понадобится 1. На больших конденсаторах емкость традиционно обозначена открытым текстом: 0,25 мкФ либо 15 uF. В этом случае, метод ее определения банален. 2. На менее больших конденсаторах (в том числе, SMD) емкость обозначается двумя либо тремя цифрами. В первом случае, она обозначена в пикофарадах. Во втором случае, первые две цифры обозначают емкость , а третья — в каких единицах она выражена:1 — десятки пикофарад;2 — сотни пикофарад;3 — нанофарады;4 — десятки нанофарад;5 — десятые доли микрофарады. 3. Существует также система обозначения емкости, использующая сочетания латинских букв и цифр. Буквы обозначают следующие цифры:A — 10;B — 11;C — 12;D — 13;E — 15;F — 16;G — 18;H — 20;J — 22;K — 24;L — 27;M — 30;N — 33;P — 36;Q — 39;R — 43;S — 47;T — 51;U — 56;V — 62;W — 68;X — 75;Y — 82;Z — 91.Полученное число следует умножить на число 10, заранее возведенное в степень, равную цифре, дальнейшей позже буквы. Итог будет выражен в пикофарадах. 4. Встречаются конденсаторы, емкость на которых не обозначена вообще. Вы наверно встречали их, в частности, в стартерах ламп дневного света. В этом случае, измерить емкость дозволено только особым прибором. Они бывают цифровыми и мостовыми.В любом случае, если конденсатор впаян в то либо иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость которого следует измерить, и лишь позже этого выпаять его. После этого его нужно подключить к прибору.На цифровом измерителе вначале выбирают самый дерзкий предел, после этого переключают его до тех пор, пока он не покажет перегрузку. Позже этого переключатель переводят на один предел назад и читают показания, а по расположению переключателя определяют, в каких единицах они выражены.На мостовом измерителе, ступенчато переключая пределы, на всем из них прокручивают регулятор из одного конца шкалы в иной, пока звук из динамика не исчезнет. Добившись исчезновения звука, по шкале регулятора считывают итог, а единицы, в которых он выражен, также определяют по расположению переключателя.После этого конденсатор устанавливают обратно в устройство. Обратите внимание! Никогда не подключайте к измерителю заряженные конденсаторы. Обнаружить значение электрического заряда дозволено двумя методами. 1-й – измерить силу взаимодействия незнакомого заряда с знаменитым и с поддержкой закона Кулона рассчитать его значение. 2-й – внести заряд в вестимое электрическое поле и измерить силу, с которой оно действует на него. Для измерения заряда происходящего через поперечное сечение проводника за определенное время измерьте силу тока и умножьте ее на значение времени. Вам понадобится 1. Измерение заряда при его взаимодействии с знаменитым зарядомЕсли знаменит заряд одного тела, поднесите к нему незнакомый заряд и измерьте расстояние между ними в метрах. Заряды начнут взаимодействовать. С поддержкой динамометра измерьте силу их взаимодействия. Рассчитайте значение неведомого заряда — для этого квадрат измеренного расстояния умножьте на значение силы и поделите на знаменитый заряд. Полученный итог поделите на число 9•10^9. Итогом будет значение заряда в Кулонах (q=F•r?/(q0•9•10^9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные. 2. Измерение значения заряда , внесенного в электрическое полеИзмерьте значение непрерывного электрического поля особым прибором (измеритель электрического поля). Если такого прибора нет, возьмите воздушный конденсатор, зарядите его, измерьте напряжение на его обкладках и поделите не расстояние между пластинами – это и будет значение электрического поля внутри конденсатора в вольтах на метр. Внесите в поле неведомый заряд. С подмогой эмоционального динамометра измерьте силу, которая на него действует. Измерение проводите в ньютонах. Поделите значение силы на напряженность электрического поля. Итогом будет значение заряда в Кулонах (q=F/Е). 3. Измерение заряда , происходящего через поперечное сечение проводникаСоберите электрическую цепь с проводниками и ступенчато подключите к ней амперметр. Замкните ее на источник тока и измерьте силу тока с подмогой амперметра в амперах. Единовременно секундомером засеките время, в течение которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, миновавший через поперечное сечение всего проводника за это время (q=I•t). При измерениях следите, дабы проводники не перегревались и не случилось короткое замыкание. Конденсатором именуется устройство, способное накапливать электрические заряды. Число накапливаемой электрической энергии в конденсаторе характеризуется его емкостью . Она измеряется в фарадах. Считается, что емкость в один фарад соответствует конденсатору, заряженному электрическим зарядом в один кулон при разности потенциалов на его обкладках в один вольт. 1. Определите емкость плоского конденсатора по формуле С = S•e•e0/d, где S — площадь поверхности одной пластины, d — расстояние между пластинами, e — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме она равна единице), e0 — электрическая непрерывная, равная 8,854187817•10(-12) Ф/м.Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, от расстояния между ними и от материала диэлектрика. В качестве диэлектрика может использоваться бумага либо слюда. 2. Относительную проницаемость диэлектриков определите по особым таблицам. Для бумаги ее величина составит 3,5, для слюды — 6,8-7,2, для фарфора — 6,5. Эта цифра показывает, во сколько раз сила взаимодействия между зарядами в данной среде поменьше, чем в вакууме. 3. Вычислите емкость сферического конденсатора по формуле С = (4П•e0•R?)/d, где П — число «пи», R — радиус сферы, d — величина зазора между его сферами.Величина емкости сферического конденсатора прямо пропорциональна радиусу концентрической сферы и обратно пропорциональна расстоянию между сферами. 4. Рассчитайте емкость цилиндрического конденсатора по формуле С = (2П•e•e0•L•R1)/(R2-R1), где L — длина конденсатора , П — число «пи», R1 и R2 — радиусы его цилиндрических обкладок. 5. Если конденсаторы в цепи объединены параллельно, рассчитайте их всеобщую емкость по формуле С = С1+С2+…+Сn, где С1, С2,…Сn – емкости параллельно объединенных конденсаторов. 6. Вычислите всеобщую емкость ступенчато объединенных конденсаторов по формуле 1/С = 1/С1+1/С2+…+1/Сn, где С1, С2,…Сn — емкости ступенчато объединенных конденсаторов. Обратите внимание! На любом конденсаторе неукоснительно должна быть нанесена маркировка, которая может быть буквенно-цифровая либо цветовая. Маркировка отражает его параметры. Емкость – величина, в системе СИ выражаемая в фарадах. Правда применяются, реально, лишь производные от нее – микрофарады, пикофарады и так дальше. Что касается электроемкости плоского конденсатора, она зависит от зазора между обкладок и их площади, от вида диэлектрика, в данном зазоре расположенного. 1. В том случае, если обкладки конденсатора имеют идентичную площадь и имеют расположение сурово одна над иной, рассчитайте площадь одной из обкладок – всякий. Если же одна из них касательно иной смещена либо они различные по площади, надобно рассчитывать площадь области, в которой обкладки друг другу перекрывают. 2. При этом применяются общепризнанные формулы, разрешающие рассчитывать площади таких геометрических фигур, как круг (S=?(R^2)), прямоугольника (S=ab), его частного случая – квадрата (S=a^2) – и других. 3. Полученная площадь непременно переводится в единицы привычной для нас системы СИ, то есть в квадратные метры. Что касается расстояния между обкладками, оно переводится, соответственно, в метры. 4. В условиях данной вам задачи может указываться как безусловная диэлектрическая проницаемость данного материала, тот, что размещен между обкладок конденсатора, так и относительная. Безусловная проницаемость выражается в Ф/м (фарады на метр), относительная же является величиной безразмерной. 5. В случае с относительной диэлектрической проницаемостью среды (диэлектрика в данном случае) применяется показатель, тот, что указывает на связь безусловной диэлектрической проницаемости материала и этой же колляции, но в вакууме, а вернее на то, во сколько раз первая огромнее 2-й. Переведите относительную диэлектрическую проницаемость в безусловную, а после этого умножьте полученный итог на электрическую непрерывную. Она составляет 8,854187817*10^(-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума. 6. Обнаружив посредством вычислений, описанных в предыдущем шаге, безусловную диэлектрическую проницаемость материала между обкладок конденсатора, если она не задана первоначально, умножьте ее на площадь той области, в которой пластины перекрывают друг другу. После этого полученный итог поделите на расстояние между обкладками, и вы получите выраженную в фарадах емкость конденсатора. 7. Если требуется, переведите полученный итог в другие единицы, больше комфортные – микро-, пико- либо нанофарады. Дозволено перевести и в миллифарады, но учтите, что в технике электроемкость в них не принято указывать, самостоятельно от того, какую конструкцию имеет тот либо другой конденсатор. Усердствуйте при выборе единицы измерения, дабы позже запятой у вас было знаков как дозволено поменьше. Видео по теме Емкость конденсатора определяется как внешними классическими геометрическими размерами прибора, а также природой и размером сердечника конденсатора, если он применяется. Вам понадобится 1. Обратите внимание на определение ёмкости конденсатора в учебнике по физике. Как знаменито, емкость конденсатора есть отношение заряда, скопленного на одной из его обкладок, к напряжению между обкладками. Таким образом, увеличить либо уменьшить емкость конденсатора дозволено, изменяя число заряда, которое он может удержать в себе при данном значении напряжения. 2. Вникните в правило действия конденсатора, дабы осознать, каким образом дозволено изменять число зарядов на его обкладках. При подаче напряжения на обкладки конденсатора внутри него создается электрическое поле, которое удерживает заряды на пластинах. Таким образом, для увеличения числа заряда на пластинах конденсатора нужно усилить электрическое поле внутри него. Для этих целей традиционно применяют вещества, именуемые поляризаторами. 3. Поляризаторы представляют собой диэлектрические вещества, атомы либо молекулы которых владеют поляризационными свойствами. Таким образом, в толще поляризатора помимо внешнего электрического поля, создаваемого зарядами обкладок, существует собственное электрическое поле, наводимое внешним. Собственное электрическое поле диэлектрика конденсатора образуется за счет идентичной ориентировки полярных частиц вещества диэлектрика. Таким образом, внутреннее электрическое поле накладывается на внешнее электрическое поле, усиливая его и создавая вероятность скапливать большее число зарядов. 4. Учтите, что разные полярные вещества способны сделать разное внутреннее электрическое поле. Таким образом, переходя от одного диэлектрика к иному, помещаемого в конденсатор, дозволено круто изменять его емкость. 5. Подметьте также, что изменить число зарядов на обкладках дозволено, легко изменив геометрические размеры прибора, а именно, изменив площадь обкладок конденсатора. Если вы обратите внимание на формулу для емкости плоскопараллельного конденсатора, вы увидите, что она представляет собой отношение площади его обкладок к расстоянию между ними, умноженное на диэлектрическую непрерывную данного вещества. Таким образом, дозволено, уменьшив расстояние между обкладками, усилить электрическое поле внутри конденсатора, тем самым увеличивая емкость конденсатора. 6. Обратите внимание, что связанность емкости конденсатора от расстояния между его платинами больше резкая, чем связанность емкости от площади обкладок. Следственно больше обоснованным является метод метаморфозы емкости посредством метаморфозы расстояния между обкладками. Видео по теме Обратите внимание! Для приобретения правильных итогов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ. jprosto.ru completerepair.ru Конденсатор представляет собой две металлические пластины, разделенные диэлектриком, поэтому постоянный ток (или постоянная составляющая тока) через конденсатор не течет! На обкладках конденсатора накапливается заряд, пропорциональный напряжению на конденсаторе. Коэффициентом пропорциональности выступает ёмкость конденсатора, обозначаемая буквой С [ф]. Если напряжение на обкладках конденсатора будет меняться, то и заряд тоже будет меняться: Изменение заряда создает в цепи конденсатора ток: Таким образом, ток, протекающий через конденсатор, равен производной от напряжения по времени, умноженной на ёмкость С. Из уравнения (1) определим напряжение на конденсаторе: Пусть на конденсатор подаётся переменное синусоидальное напряжение Из этого выражения видно, что на конденсаторе синусоидальный ток Амплитуда тока связана с амплитудой напряжения следующим соотношением: Это соотношение очень напоминает закон Ома. Поэтому введём понятие ёмкостного реактивного сопротивления: Если поделить левую и правую часть уравнения (3) на Производная от Подсчитаем значение средней за период мощности (активной мощности): Графики Как видно из графика, мгновенная мощность на конденсаторе изменяется синусоидально с удвоенной частотой. Четверть периода конденсатор запасает энергию Произведение Поскольку эта мощность не совершает полезной работы, её называют реактивной, и сопротивление Как правило, за начальную фазу принимают фазу тока, поэтому первые четверть периода мгновенная мощность отрицательна. Реактивная мощность конденсатора при расчетах берется со знаком «–», она отрицательна. В электротехнике часто синусоидальные токи и напряжения представлены в виде векторов, длина которых равна амплитуде или действующему значению, а угол поворота соответствует фазе. Такой вектор будет вращаться с частотой Как найти напряжение между пластинами конденсатора. Как найти напряжение на конденсаторе
Как найти напряжение между пластинами конденсатора

Инструкция

Инструкция

Инструкция

Инструкция

Инструкция

Инструкция
Как найти напряжение между пластинами конденсатора
Одним из разделов физики, лежащих в основе знания, посвященного процессам, связанным с электричеством, является электростатика. Она изучает взаимодействие неподвижных электрических зарядов. Поэтому одной из типичных задач, которую может потребоваться решить школьникам и студентам младших курсов ВУЗ-ов, является нахождение напряжения между пластинами конденсатора на основании знания различных параметров. Вам понадобится
Инструкция
Переменный ток в конденсаторе

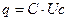 . Размерность ёмкости – фарада. Это очень большая величина, поэтому используются её производные
. Размерность ёмкости – фарада. Это очень большая величина, поэтому используются её производные 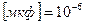 ;
; 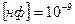 ;
;  .
.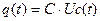
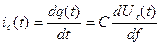 (1)
(1)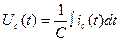 (2)
(2) . Определим ток конденсатора по формуле (1):
. Определим ток конденсатора по формуле (1):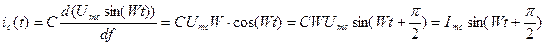
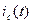 опережает по фазе напряжение
опережает по фазе напряжение  на угол
на угол 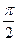 (или 90°).
(или 90°).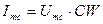 или
или 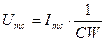
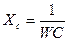 , тогда
, тогда 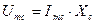 (3)
(3)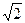 , то получим:
, то получим: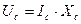 , где
, где  и
и  – действующие значения напряжения и тока конденсатора. Конденсатор способен накапливать энергию:
– действующие значения напряжения и тока конденсатора. Конденсатор способен накапливать энергию: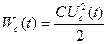 (это энергия электрического поля в конденсаторе)
(это энергия электрического поля в конденсаторе)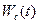 – есть мгновенная мощность:
– есть мгновенная мощность:
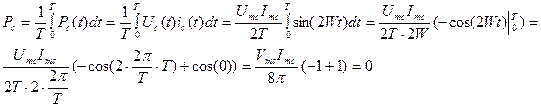
 ,
,  ,
,  показаны на рис. 1.
показаны на рис. 1.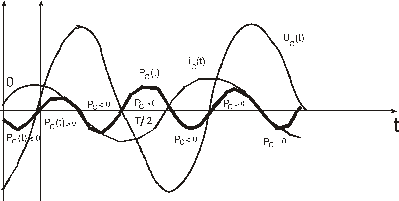
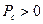 , а следующую четверть периода – отдает обратно в цепь
, а следующую четверть периода – отдает обратно в цепь 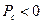 , поэтому активная мощность конденсатора (идеального, без потерь) равна нулю.
, поэтому активная мощность конденсатора (идеального, без потерь) равна нулю.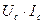 дает величину реактивной мощности конденсатора, обозначаемой
дает величину реактивной мощности конденсатора, обозначаемой 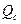 . Эта величина определяет среднее значение мощности, запасаемой в конденсаторе энергии.
. Эта величина определяет среднее значение мощности, запасаемой в конденсаторе энергии.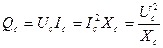
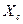 – тоже называют реактивным.
– тоже называют реактивным. , чтобы его остановить полагают
, чтобы его остановить полагают 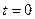 , тогда угол поворота будет равен начальной фазе g, для конденсатора
, тогда угол поворота будет равен начальной фазе g, для конденсатора 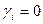 ;
; 

Похожие статьи:
poznayka.org
Конденсатор в цепи постоянного тока
Заряд конденсатора через резисторПри подключении конденсатора к источнику постоянного тока под действием электрического поля на нижнюю обкладку движутся электроны. В следствии, явления электростатической индукции с верхней обкладки конденсатора заряды уходят к положительному выводу источника питания в цепи возникает ток – ток заряда по мере накопления зарядов в конденсаторе, растёт напряжение , а ток заряда уменьшается, и так, – конденсатор подключённый к источнику тока, заряжается до Uист.
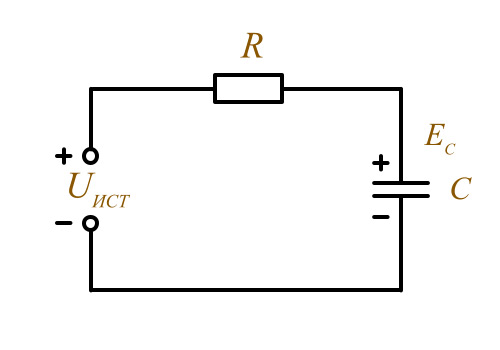
Конденсатор в цепи постоянного тока
Кратковременный ток в цепи называется ток заряда, а так как он существует короткое время, то говорят, конденсатор постоянный ток не пропускает.
Считается что конденсатор заряжается если напряжение на нём составляет 0,63 от Uист и это происходит за время равное Τ
Ес – ЭДС ёмкости
Τ заряда – постоянная времени заряда конденсатора в секундах
Одна секунда – 1с = 103мс = 106мкс =1012нс
Rзар – сопротивление в Омах
С – ёмкость в Фарадах
Τ = Rзар × С
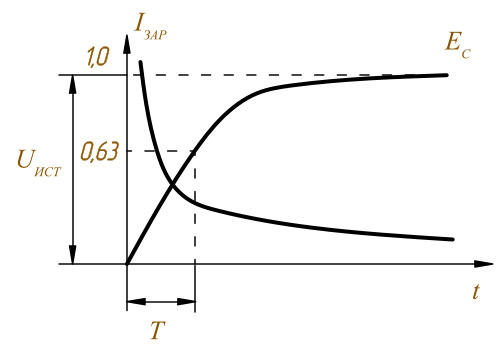
График заряда конденсатора
Разряд конденсатора через резистор
Работа конденсатора в цепи постоянного тока
Считается, что конденсатор разрядится если напряжение на нём составляет 0,37 от напряжения источника и это происходит за время Τ разряда.
Τразр = Rразр × С
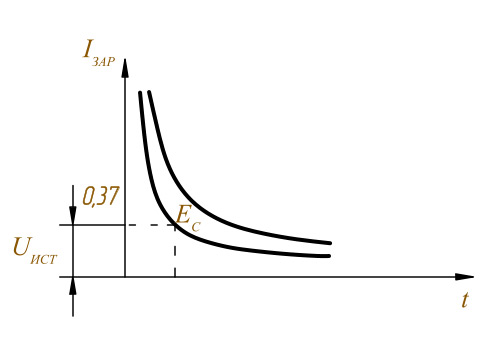
График разряда конденсатора
selectelement.ru



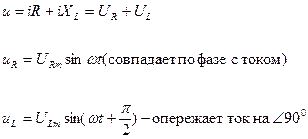







Поделиться с друзьями: