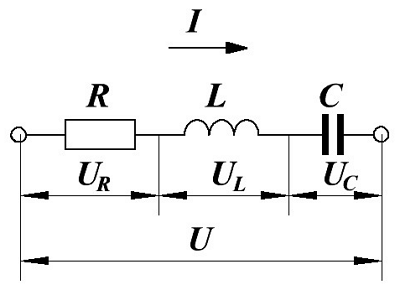
Электрические цепи постоянного тока и методы их расчета (стр. 1 из 6). Как найти напряжение в цепи

Электрические цепи постоянного тока и методы их расчета

1.1. Электрическая цепь и ее элементы

В электротехнике рассматривается устройство и принцип действия основных электротехнических устройств, используемых в быту и промышленности. Чтобы электротехническое устройство работало, должна быть создана электрическая цепь, задача которой передать электрическую энергию этому устройству и обеспечить ему требуемый режим работы.

Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.

Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис. 1.1.

Рис. 1.1

Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы:

1) Источники электрической энергии (питания).

Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).

2) Потребители электрической энергии.

Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой.

3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.

Все элементы цепи охвачены одним электромагнитным процессом.

В электрической схеме на рис. 1.1 электрическая энергия от источника ЭДС E, обладающего внутренним сопротивлением r0 , с помощью вспомогательных элементов цепи передаются через регулировочный реостат R к потребителям (нагрузке): электрическим лампочкам EL1 и EL2 .

1.2. Основные понятия и определения для электрической цепи

Для расчета и анализа реальная электрическая цепь представляется графически в виде расчетной электрической схемы (схемы замещения). В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают. Источник питания показывается как источник ЭДС E с внутренним сопротивлением r0 , реальные потребители электрической энергии постоянного тока заменяются их электрическими параметрами: активными сопротивлениями R1 , R2 , …, Rn . С помощью сопротивления R учитывают способность реального элемента цепи необратимо преобразовывать электроэнергию в другие виды, например, тепловую или лучистую.

При этих условиях схема на рис. 1.1 может быть представлена в виде расчетной электрической схемы (рис. 1.2), в которой есть источник питания с ЭДС E и внутренним сопротивлением r0 , а потребители электрической энергии: регулировочный реостат R, электрические лампочки EL1 и EL2 заменены активными сопротивлениями R, R1 и R2 .

Рис. 1.2

Источник ЭДС на электрической схеме (рис. 1.2) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС.

При расчете в схеме электрической цепи выделяют несколько основных элементов.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Схема на рис. 1.2 имеет три ветви: ветвь bma, в которую включены элементы r0 , E, R и в которой возникает ток I; ветвь ab с элементом R1 и током I1 ; ветвь anb с элементом R2 и током I2 .

Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 1.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R1 и R2 (рис. 1.2) находятся в параллельных ветвях.

Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 1.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.

Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 1.2) стрелками укажем положительные направления ЭДС, напряжений и токов:

а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;

б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;

в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи.

Все электрические цепи делятся на линейные и нелинейные.

Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь.

Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.

Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент.

1.3. Основные законы цепей постоянного тока

Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.

Закон Ома для участка цепи

Соотношение между током I, напряжением UR и сопротивлением R участка аb электрической цепи (рис. 1.3) выражается законом Ома

Рис. 1.3

(1.1)

или UR = RI.

В этом случае UR = RI – называют напряжением или падением напряжения на резисторе R, а

– током в резисторе R.

При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:

В этом случае закон Ома для участка цепи запишется в виде:

I = Uq.

Закон Ома для всей цепи

Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис. 1.3), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи:

(1.2)

Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

(1.3)

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2) I - I1 - I2 = 0.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

(1.4)

где n – число источников ЭДС в контуре;m – число элементов с сопротивлением Rк в контуре;Uк = Rк Iк – напряжение или падение напряжения на к-м элементе контура.

Для схемы (рис. 1.2) запишем уравнение по второму закону Кирхгофа:

E = UR + U1 .

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю

(1.5)

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

mirznanii.com

Как вычислить напряжение, силу тока и сопротивление в параллельной цепи » VripMaster

В параллельной цепи резисторы соединены таким образом, что электрический ток в цепи делится между резисторами и проходит через них одновременно (сравните это с автодорогой, которая разделяется на две параллельные дороги и делит поток машин на два потока, движущихся параллельно друг другу). Эта статья расскажет вам, как вычислить напряжение, силу тока и сопротивление в параллельной цепи.

Часть 1 из 3: Параллельные цепи

Определение. Параллельная цепь – это цепь, в которой ток течет из точки А в точку В одновременно по нескольким элементам цепи (то есть поток электронов разбивается на несколько потоков, которые на конечном участке цепи вновь объединяются в единый поток). В большинстве задач, в которых присутствует параллельная цепь, нужно вычислить напряжение, сопротивление и силу тока.
- Элементы, подключенные параллельно, находятся на отдельных ветвях цепи.
Сила тока и сопротивление в параллельных цепях. Представьте себе автостраду с несколькими полосами, на каждой из которых установлен пункт пропуска, замедляющий движение автомобилей. Построив новую полосу, вы увеличите скорость движения (даже если и на этой полосе вы поставите пункт пропуска). Аналогично с параллельной цепью – добавив новую ветвь, вы уменьшите общее сопротивление цепи и увеличите силу тока.
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть если вы знаете силу тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + ...
Общее сопротивление в параллельной цепи. Оно вычисляется по формуле: /RT = /R1 + /R2 + /R3 + ..., где R1, R2 и так далее – это сопротивление соответствующих элементов (резисторов) этой цепи.
- Например, параллельная цепь включает два резистора и сопротивление каждого равно 4 Ом. /RT = /4 + /4 → /RT = /2 → RT = 2 Ом. То есть общее сопротивление параллельной цепи с двумя элементами, сопротивления которых равны, в два раза меньше сопротивления каждого резистора.
- Если какая-либо ветвь параллельной цепи не имеет сопротивления (0 Ом), то весь ток пройдет именно через эту ветвь.
Напряжение. Напряжение – это разность электрических потенциалов между двумя точками электрической цепи. Так как здесь рассматриваются две точки без учета пути движения тока по цепи, напряжение в параллельной цепи одинаково на каждом элементе этой цепи, то есть: VT = V1 = V2 = V3 = ...
Вычислите значения неизвестных величин по закону Ома. Закон Ома описывает взаимосвязь между напряжением V, силой током I и сопротивлением R: V = IR. Если вам известны значения двух величин из этой формулы, вы можете найти значение третьей величины.
- Вы можете применить закон Ома для всей цепи (V = ITRT) или для одной ветви этой цепи (V = I1R1).

Часть 2 из 3: Пример цепи

Нарисуйте таблицу, чтобы облегчить решение задачи, особенно если неизвестны значения сразу нескольких величин в данной параллельной цепи. Рассмотрим пример электрической цепи с тремя параллельными ветвями. Обратите внимание, что здесь под ветвями подразумеваются резисторы с сопротивлениями R1, R2, R3. R1 R2 R3 Общее Единицы измерения V В I А R Ом
Внесите в таблицу данные вам значения. Например, к электрической цепи подключена батарея, напряжение которой равно 12 В. Цепь включает три параллельные ветви с сопротивлениями 2 Ом, 4 Ом, 9 Ом. R1 R2 R3 Общее Единицы измерения V 12 В I А R 2 4 9 Ом
Заполните значения напряжения для каждого элемента цепи. Помните, что общее напряжение в параллельной цепи и напряжение на каждом резисторе этой цепи равны. R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I А R 2 4 9 Ом
Вычислите силу тока на каждом резисторе по закону Ома. Так как теперь в каждом столбце вашей таблицы есть значения двух величин, вы с легкостью вычислите значение третей величины при помощи закона Ома: V = IR. В нашем примере нужно найти силу тока, поэтому перепишите формулу закона Ома следующим образом: I = V/R R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 12/2 = 6 12/4 = 3 12/9 = ~1,33 А R 2 4 9 Ом
Вычислите общую силу тока. Помните, что общая сила тока в параллельной цепи равна сумме сил тока на каждом элементе этой цепи. R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1,33 6 + 3 + 1,33 = 10,33 А R 2 4 9 Ом
Вычислите общее сопротивление. Сделайте это одним из двух способов. Либо используйте формулу /RT = /R1 + /R2 + /R3, либо формулу закона Ома: R = V/I. R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1.33 10,33 А R 2 4 9 12 / 10,33 = ~1,17 Ом

Часть 3 из 3: Дополнительные вычисления

Вычислите мощность тока по формуле: P = IV. Если вам дана мощность тока на каждом участке цепи, то общая мощность вычисляется по формуле: PT = P1 + P2 + P3 + ....
Вычислите общее сопротивление в параллельной цепи, состоящей из двух ветвей (двух резисторов).
Найдите общее сопротивление в параллельной цепи, если сопротивление всех резисторов одинаково: RT = R1 / N, где N – количество резисторов в цепи.
- Например, если в параллельной цепи два резистора с одинаковым сопротивлением, то общее сопротивление цепи будет вдвое меньше сопротивления одного резистора. Если в цеп

vripmaster.com

Показать содержимое по тегу: электротехника

В связи с широким развитием вычислительных устройств задача расчета и моделирования электрических схем заметно упростилась. Наиболее подходящим программным обеспечением для данных целей является продукт National instruments – Multisim (Electronic Workbench ).

В данной статье рассмотрим простейшие примеры моделирования электрических схем с помощью Multisim.

Итак, у нас имеется Multisim 12 это последняя версия на момент написания статьи. Откроем программу и создадим новый файл с помощью сочетания Ctrl+N.

После создания файла перед нами открывается рабочая зона. По сути, рабочая зона Multisim – это поле для собирания требуемой схемы из имеющихся элементов, а их выбор, поверьте велик.

Кстати вкратце о элементах. Все группы по умолчанию расположены на верхней панели. При нажатии на какую либо группу, перед вами открывается контекстное окно, в котором вы выбираете интересующий вас элемент.

По умолчанию используется база элементов – Master Database. Компоненты содержащиеся в ней разделены на группы.

Перечислим вкратце содержание групп.

Sources содержит источники питания, заземление.

Basic – резисторы, конденсаторы, катушки индуктивности и т.д.

Diodes – содержит различные виды диодов.

Transistors - содержит различные виды транзисторов.

Analog - содержит все виды усилителей: операционные, дифференциальные, инвертирующие и т.д.

TTL - содержит элементы транзисторно-транзисторная логики

CMOS - содержит элементы КМОП-логики.

MCU Module – управляющий модуль многопунктовой связи.

Advanced_Peripherals – подключаемые внешние устройства.

Misc Digital - различные цифровые устройства.

Mixed - комбинированные компоненты

Indicators - содержит измерительные приборы и др.

С панелью моделирования тоже ничего сложного, как на любом воспроизводящем устройстве изображены кнопки пуска, паузы, останова. Остальные кнопки нужны для моделирования в пошаговом режиме.

На панели приборов расположены различные измерительные приборы (сверху вниз) - мультиметр, функциональный генератор, ваттметр, осциллограф, плоттер Боде, частотомер, генератор слов, логический конвертер, логический анализатор, анализатор искажений, настольный мультиметр.

Итак, бегло осмотрев функционал программы, перейдём к практике.

Пример 1

Для начала соберём простенькую схему, для этого нам понадобиться источник постоянного тока (dc-power) и пара резисторов (resistor).

Допустим нам необходимо определить ток в неразветвленной части, напряжение на первом резисторе и мощность на втором резисторе. Для этих целей нам понадобятся два мультиметра и ваттметр. Первый мультиметр переключим в режим амперметра, второй – вольтметра, оба на постоянное напряжение. Токовую обмотку ваттметра подключим во вторую ветвь последовательно, обмотку напряжения параллельно второму резистору.

Есть одна особенность моделирования в Multisim – на схеме обязательно должно присутствовать заземление, поэтому один полюс источника мы заземлим.

После того как схема собрана нажимаем на пуск моделирования и смотрим показания приборов.

Проверим правильность показаний (на всякий случай=)) по закону Ома

Показания приборов оказались верными, переходим к следующему примеру.

Пример 2

Соберём усилитель на биполярном транзисторе по схеме с общим эмиттером. В качестве источника входного сигнала используем функциональный генератор (function generator). В настройках ФГ выберем синусоидальный сигнал амплитудой 0,1 В, частотой 18,2 кГц.

С помощью осциллографа (oscilloscope) снимем осциллограммы входного и выходного сигналов, для этого нам понадобится задействовать оба канала.

Чтобы проверить правильность показаний осциллографа поставим на вход и на выход по мультиметру, переключив их предварительно в режим вольтметра.

Запускаем схему и открываем двойным кликом каждый прибор.

Показания вольтметров совпадают с показаниями осциллографа, если знать что вольтметр показывает действующее значение напряжения, для получения которого необходимо разделить амплитудное значение на корень из двух.

Пример 3

С помощью логических элементов 2 И-НЕ соберём мультивибратор, создающий прямоугольные импульсы требуемой частоты. Чтобы измерить частоту импульсов воспользуемся частотомером (frequency counter), а проверим его показания с помощью осциллографа.

Итак, допустим, мы задались частотой 5 кГц, подобрали опытным путём требуемые значения конденсатора и резисторов. Запускаем схему и проверяем, что частотомер показывает приблизительно 5 кГц. На осциллограмме отмечаем период импульса, который в нашем случае равен 199,8 мкс. Тогда частота равна

Мы рассмотрели только малую часть всех возможных функций программы. В принципе, ПО Multisim будет полезен как студентам, для решения задач по электротехнике и электронике, так и преподавателям для научной деятельности и т.д.

Надеемся данная статья оказалась для вас полезной. Спасибо за внимание!

electroandi.ru

Как вычислить напряжение в цепи

Есть некоторые важные профессии, где для работы требуется правильно произвести вычисление напряжения в сети. Для осуществления данной операции используется специальная формула, то есть определенный метод вычисления. В любой параллельной цепи все резисторы соединены строго таким образом, что ток в сети распределяется между ними одинаково в процессе прохождения через данные устройства. Подобное движение можно сравнить с обычной автомобильной трассой, которая время от времени разделяется на две параллельные дороги, соответственно транспортные средства, перемещающиеся по ней, делятся на два потока. Чтобы вычислить неизвестное значение напряжения, используется специальная формула, основанная на законе Ома. Выглядит она следующим образом - V=I*R, где I сила тока, а R сопротивление. Данное вычисление можно произвести только при условии, что оба эти параметры известны. Итак, если известен уровень сопротивления, а также сила тока, достаточно просто подставить их в данную формулу. Стоит отметить, что полученное значение для всех подключенных резисторов будет одинаковым.

Все довольно просто, если присутствуют два из трех неизвестных. Ситуация немного усложниться, если сопротивление или сила тока будут неизвестны. R определяется по следующей формуле R = R1*R2/(R1+R2). При необходимости вычислить силу тока при известных двух показателях, можно применить формулу I=V/R. Все подобные процессы можно произвести при помощи обычного калькулятора. При необходимости можно вычислить силу тока в каждом из установленных резисторов.В процессе определения уровня напряжения в сети рекомендуется записывать все полученные результаты производимых вычислений на бумажный носитель, это касается силы тока и сопротивления. В ситуации, если в задаче была дана параллельная и одновременно последовательная цепь, стоит сделать все вычисление специальным методом. Узнать о нем можно в любом техническом учебнике. Сначала рассчитывается параллельный участок, а затем следует умножить полученный результат на общее их количество в последовательной сети. В некоторых источниках можно встретить формулы в такими данными, как V1, I1, R1. Они означают определенные величины, характерные для какого-то одного конкретного резистора проводника. Если же указаны такие параметры, как V, I, R, нужно знать, что это обычные общие суммарные данные. Общий показатель силы тока равен сумме подобных параметров в каждом из проводников. Что касается мощности, то она вычисляется также обычным сложением, говоря иными словами, это результат их прибавления. Чтобы решить задачи такого плана, профессионалы рекомендуют применять примеры, указанные в обычных школьных учебниках. При этом не стоит забывать указывать единицы измерения, предназначенные для вычисления данных величин. Важно помнить, что если напряжение требуется узнать для параллельной цепи, полученные в результате параметры будут одинаковыми для всех установленных устройств, характеризующихся, как резисторы.

completerepair.ru

Каталог товаров