Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока. Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω. В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно, Im – амплитудное значение переменного тока. Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде где R – активное сопротивление, Х – реактивное сопротивление. Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер. В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым. При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение где Z – полное сопротивление цепи, ψ – разность фаз между напряжением и током. Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением где Um – амплитудное значение переменного напряжения, Im – амплитудное значение переменного тока, Z – полное сопротивление цепи. Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока. Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно, Um – амплитудное значение переменного тока. Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения где g – активная проводимость, b – реактивная проводимость. Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной. Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым. Определим зависимость между напряжением и силой тока в параллельной цепи где y – полная проводимость, ψ – разность фаз между напряжением и током в цепи. Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид где Um – амплитудное значение переменного напряжения, Im – амплитудное значение переменного тока, y – полная проводимость цепи. Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения. Мгновенная мощность в цепи будет равна Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока). Теперь определим среднее значение мощности за период или активную мощность, которая будет равна где U – действующее значение переменного напряжения, I – действующее значение переменного тока, cos(φ) – коэффициент мощности. Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности. При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I). Теория это хорошо, но теория без практики - это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками Скажи спасибо автору нажми на кнопку социальной сети www.electronicsblog.ru Цепь переменного тока при последовательном соединении элементов. Напряжение в последовательной цепи
Соединение элементов в цепи переменного напряжения и тока
Последовательное соединение элементов цепи при переменном напряжении
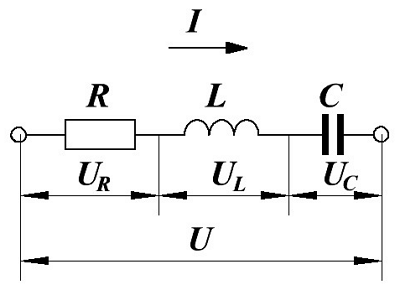 Последовательное соединение элементов цепи.
Последовательное соединение элементов цепи. 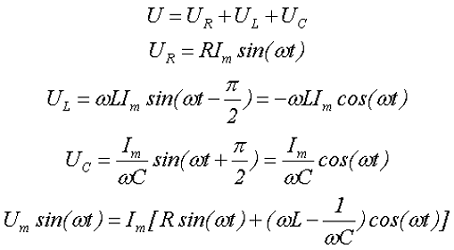
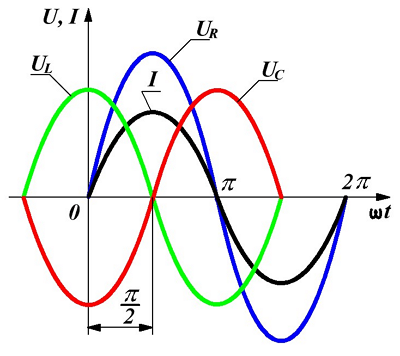 Напряжения и токи при последовательном соединении.
Напряжения и токи при последовательном соединении. 


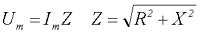
Параллельное соединение элементов цепи при переменном напряжении
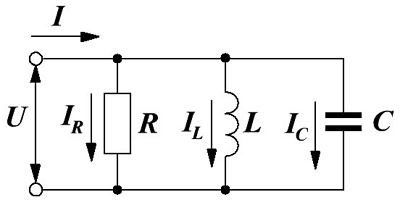 Параллельно соединение элементов цепи.
Параллельно соединение элементов цепи. 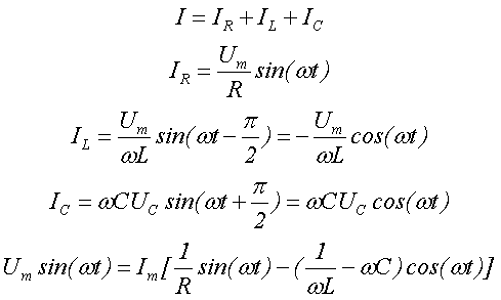
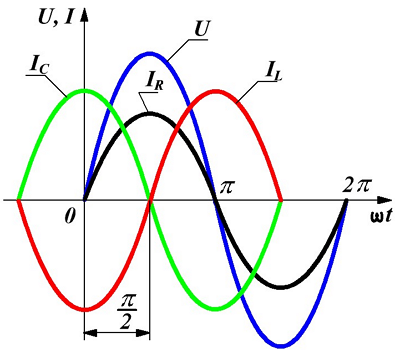 Напряжение и токи при параллельном соединении.
Напряжение и токи при параллельном соединении. 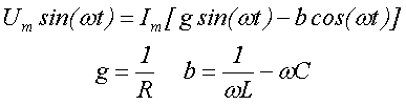
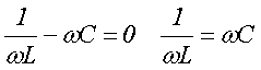
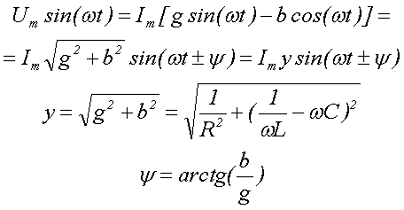

Чему равна мощность в цепи при синусоидальном напряжении?

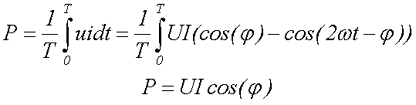
Цепь переменного тока при последовательном соединении элементов
i=Imsinωt
При последовательном соединении элементов ток на всех участках цепи одинаков. Действующее значение тока и угловую частоту ω можно найти, используя закон изменения токаi=Imsinωt
Падение напряжения на каждом элементе цепи можно определить из закона Ома
UR = I R ; UL = I XL = I 2π f L = I ωL; UC = I XC =
Приложенное напряжение Uравно геометрической сумме падений напряжения на каждом элементе последовательной цепи (IIзакона Кирхгофа).
– сумма геометрическая (векторная), следовательно, необходимо построить векторную диаграмму (ВД)
Порядок построения ВД:
Строим вектор тока
Относительно вектора тока строим вектор падения напряжения на первом элементе цепи, учитывая величину и направление угла сдвига фаз между током и напряжением.
Из конца этого вектора аналогично строим вектор падения напряжения на следующем элементе цепи и т.д. – в результате получим векторную сумму падений напряжения на всех элементах цепи, т.е. приложенное напряжение .
ВД при резонансе напряжений
φ= 0
Численное значение приложенного напряжения Uможно определить из ВД
=
Где: – полное сопротивление цепи
– эквивалентное активное сопротивление цепи
– эквивалентное реактивное сопротивление цепи
Резонанс в последовательной цепи (резонанс напряжений)
При резонансе напряжений сумма индуктивных напряжений равна сумме емкостных, следовательно, эквивалентное реактивное напряжение
– условие резонанса напряжений
Следовательно, при резонансе напряжений
Приложенное напряжение – равно активному.
Полное сопротивление цепи – равно сумме активных сопротивлений и минимально, т.е. всю цепь можно заменить эквивалентным активным сопротивлениемRЭ.
Ток в цепи – максимален, и падение напряжения на отдельных реактивных элементах может быть больше приложенного напряжения (см. ВД при резонансе).
При резонансе напряжений приложенное напряжение совпадает по фазе с током (φ = 0), т.е. несмотря на наличие реактивных элементов, цепь ведет себя как чисто активный приемник.
Цепь переменного тока при параллельном соединении элементов
При параллельном соединении элементов напряжение на каждой ветви схемы одинаково и равно приложенному. Каждая ветвь схемы представляет из себя последовательное соединение элементов, следовательно, можно для каждой из ветвей найти полное сопротивление Z, токIи угол сдвига фаз φ
Аналогично можно определить Z,Iи φ для остальных ветвей
По Iзакону Кирхгофа ток в неразветвленной части цепи равен геометрической сумме токов в ветвях–сумма геометрическая (векторная), следовательно, необходимо построить векторную диаграмму (ВД).
Порядок построения ВД:
Строим вектор напряжения
Относительно вектора напряжения строим вектор тока первой ветви , учитываявеличину и направление угла сдвига фаз между током и напряжением φ1.
Из конца этого вектора строим вектор тока второй ветви и т.д. – в результате получим векторную сумму токов в ветвях, т.е. ток в неразветвленной части цепи.
Численное значение полного тока Iможно определить из ВД, если разложить ток каждой ветви на две составляющие
Например, для первой ветви
– активная составляющая токаI1
– реактивная составляющая токаI1
– активная проводимость отдельной ветви
– реактивная проводимость отдельной ветви
Аналогично можно разложить на составляющие токи всех ветвей
Тогда из ВД, учитывая, что емкостные и индуктивные токи направлены в противоположные стороны, получим
=
=
Где: – активная составляющая полного тока
– реактивная составляющая полного тока
– эквивалентная активная проводимость цепи
– эквивалентная реактивная проводимость цепи
– полная проводимость цепи
Резонанс в параллельной цепи (резонанс токов)
При резонансе токов сумма индуктивных токов равна сумме емкостных, следовательно, реактивная составляющая полного тока
– условие резонанса токов
Следовательно, при резонансе токов
Полный ток (в неразветвленной части цепи) – равен активному, т.е. сумме активных токов всех ветвей.
Полная проводимость цепи – равно сумме активных проводимостей всех ветвей и минимальна.
Ток в цепи – минимален, т.е. параллельная цепь при резонансе обладает минимальной проводимостью, т.е. максимальным сопротивлением.
При резонансе токов полный ток совпадает по фазе с приложенным напряжением (φ = 0), т.е. вся цепь имеет чисто активный характер.
studfiles.net
Почему последовательная цепь сопротивлений называется делителем напряжений.
Тема: что такое делитель электрического напряжения, его суть, принцип действия.
Чтобы понять, почему именно последовательную цепь, состоящую из электрических сопротивлений, называют делителем напряжений давайте с Вами разберемся в основах электрофизики. Хотя, если вдуматься в само название этого вопроса, можно и самому догадаться, что если имеется последовательная цепь из резисторов, то на каждом из них по идее должно оседать какая-то определённая часть электрического напряжения. Следовательно, мы как бы делим одно общее напряжение на некоторые его части, величина которых нам нужна для каких-то своих нужд.
Итак, электрическое напряжение — это разность электрических потенциалов между двумя различными точками. Если взять обычный резистор (имеющее некоторое сопротивление, пусть 10 Ом), и к нему приложить напряжение, к примеру величиной в 12 вольт, то через резистор потечет электрический ток величиной в 1,2 ампера (по закону ома мы напряжение делим на сопротивление). При этом если щупами вольтметра прикоснутся к выходу источника питания, а потом непосредственно к нашему резистору, то убедимся, что напряжение будут совпадать (возможно с очень малой разницей по причине оседания напряжения на самих проводах, если они достаточно длинны).
Теперь вместо одного резистора на 10 Ом мы поставим два последовательно соединенных резистора, каждый из которых по 5 Ом (при последовательном соединении сопротивлений их номиналы слаживаются). Подсоединив всё тот же блок питания на 12 вольт и измерив напряжение на каждом из резисторов мы увидим что напряжение поделилось поровну. На каждом резисторе осело ровно по 6 вольт. Это потому что сопротивления одинаковой величины. Если мы поставили три одинаковых резистора то и напряжение разделилось бы поровну на три части (по 4 вольта). Ну думаю смысл деления понятен.
А что если резисторы будут разной величины (соединение их также последовательное) ? Тогда электрическое напряжение поделится прямо пропорционально их сопротивлению. Узнать на каком какое осядет напряжения можно либо просто измерив его вольтметром, либо же путём применения формулы закона Ома, но для этого мы должны знать силу тока, что будет протекать по этой последовательной цепи. И чтобы узнать напряжение на резисторе нужно силу тока (в Амперах) умножить на его сопротивление (в Омах). Ну, и так для каждого резистора, где нужно узнать напряжение.
На примере последовательно соединённых резисторов мы увидели сам принцип деления напряжения. Более распространенным вариантом делителя напряжения является использование переменного (подстроечного) резистора, имеющего три вывода (два основных, имеющие общее сопротивление данного резистора и один вывод, идущий от ползунка, смещающегося между этими двумя основными). В схемах делителя напряжения его подключают так: один вывод (из основных) является общим, второй из основных является местом, куда прилаживается общее напряжение, ну, а с вывода, идущего от ползунка, относительно общего провода, снимается более низкое напряжение, величину которого можно выставить ручкой этого переменного резистора. Данный вариант делителя напряжения повсеместно используется в регуляторах громкости, тембра и т.д.
Итак, мы выяснили, что приложенное электрическое напряжение на цепочку последовательно соединенных резисторов будет делится пропорционально сопротивлению, которым обладает каждый из них. Может возникнуть вопрос (если коснуться практического применения делителя напряжения в конкретных схемах), а что при этом сопротивления могут быть совсем разные? Для получения нужной величины именно напряжения, то да, лишь бы соблюдался принцип пропорциональности. Но вот если в схеме имеет значение сила тока, текущего через этот самый делитель напряжения, то тут уж величина сопротивлений имеет значение.
Допустим нам нужно использовать делитель напряжения для регулируемого блока питания. В обычной схеме такого блока питания имеется параметрический стабилизатор в виде опорного стабилитрона. Стабилитроны не рассчитаны на большие токи (через них в рабочем состоянии протекают десятки миллиампер). Следовательно параллельно подключенный к стабилитрону делитель напряжения (в виде обычного переменного резистора) также не будет пропускать через себя большие токи. Посему номинал переменного резистора для делителя напряжения берется обычно в пределах 1-10 килоОм.
В электрических схемах делители напряжения встречаются на каждом шагу. Именно эти делители позволяют получать нужное значения электрического напряжения в тех или иных узлах схемы. В более простом варианте роль данного делителя выполняют обычные постоянные и переменные резисторы. Хотя при усложнении схемы уже могут использоваться цифровые варианты и аналоги, что дает свои преимущества.
P.S. Понимая общий принцип работы и само назначение делителя напряжения вы уже легко сможете распознавать эту функциональную часть в различных электрических и электронных схемах. При некоторой практике сами начнете широко их использовать в тех или иных схемах (обычно начинают с самодельных регулируемых блоков питания).
electrohobby.ru
Последовательная RL-цепь
Рассмотрим цепь, состоящую из последовательно соединенных резистора R и катушки L, в электротехнике такая цепь часто называется последовательной RL-цепью.

Напряжение, приложенное к цепи равно

По второму Кирхгофа, для рассматриваемой цепи можно записать выражение

Напряжение на резисторе и катушке равно

Тогда напряжение, приложенное к цепи

Ток в цепи равен

Подставив ток в выражение для напряжения, получим

или

Из выше приведенной формулы первое слагаемое это напряжение на резисторе, то есть

Из этого можно сделать вывод, что ток и напряжение в резисторе совпадают по фазе.
Напряжение на катушке

Напряжение на катушке опережает ток на угол π/2.
Реактивное сопротивление катушки равно

Сопротивление катушки зависит от частоты. При постоянном токе, частота равна нулю, а значит и сопротивление тоже.
Сдвиг фаз RL-цепи можно определить по формуле

Полное сопротивление RL-цепи

Амплитудное значение тока

Рассмотрим пример
К цепи, состоящей из последовательно соединенных катушки и резистора приложено синусоидальное напряжение. Ток в цепи равен 1,2 А. Сопротивление резистора 10 Ом, индуктивность катушки 26 мГн. Найдите напряжение U, UR, UL, сдвиг фаз φ. Постройте векторную диаграмму.
Найдем напряжение на каждом из элементов, зная ток в цепи и их сопротивление

Найдем сдвиг фаз между током и напряжением в цепи. В нашем случае реактивное сопротивление x состоит только из индуктивного сопротивления xL

Построим векторную диаграмму напряжений для нашей цепи. Подробнее об этом в статье Построение векторных диаграмм.

Напряжение в цепи найдем из треугольника напряжений

Спасибо за внимание! Рекомендуем - Последовательная RC-цепь
electroandi.ru










Поделиться с друзьями: