В этой главе… Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало). Итак, самое время обратиться к термодинамике. Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.) Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!) Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна. Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала. Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует. Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия \( Q \), а сама система выполняет над окружающими телами работу \( W \) (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение \( U_н \), становится равной \( U_к \) следующим образом: В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы. На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное \( Q \), то при отсутствии работы ее количество внутренней энергии, обозначаемое как \( U \), изменится на \( Q \). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия \( U \) изменится на \( W \). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется. Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью. Величина передаваемой тепловой энергии \( Q \) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы \( W \) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой. Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж. Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии: Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки: В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой: а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение \( W \) считается отрицательным. Таким образом, получаем: В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа. В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия). Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы. Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным. Какую работу выполняет система при расширении газа? Работа равна произведению \( F \) на \( s \), означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению \( P \) на \( A \), означающих, соответственно, давление и площадь. Это значит, что: Но произведение площади \( A \) и перемещения \( s \) равно изменению объема \( \Delta\!V \). Таким образом: Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как \( W=P\Delta\!V \), то работа — это площадь, ограниченная графиком. Допустим, имеется 60 м3 идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м3 (\( PV= nRT \), где \( n \), \( R \) и \( Т \) означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения: Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж. А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется). Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому \( Fs \) (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю. В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как \( PV= nRT \) (см. главу 14), то температура также остается постоянной. Какая работа выполняется при изменении объема? Поскольку \( PV= nRT \), то получается такое отношение между \( P \) и \( V \): Эту формулу иллюстрирует график, показанный на рис. 15.6. Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где \( ln \) — натуральный логарифм, \( R \) — газовая постоянная (8,31), \( V_1 \) и \( V_0 \) означают, соответственно, конечный и начальный объем: Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна \( (3/2)nRT \) (см. главу 14), то эта энергия не меняется. Таким образом: другими словами: Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия \( Q \), а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с \( V_0 \) = 0,010 м3 до \( V_1 \) = 0,020 м3. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения: Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как \( Q=W \), то добавляемая к газу тепловая энергия также равна 1690 Дж. При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим. Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что \( Q \) = 0, таким образом: Так как внутренняя энергия \( U \) идеального газа равна \( (3/2)nRT \) (см. главу 14), то выполняется работа: где \( T_0 \) и \( T_1 \) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8). Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле: Что такое \( \gamma \)? Это отношение \( C_p/C_v \) двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении \( C_p \), а в знаменателе — теплоемкость при постоянном объеме \( C_v \). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии \( Q \), необходимой для изменения температуры тела единичной массы на величину \( \Delta T \), т.е. \( c=Q/m\Delta T \), где \( c \), \( m \) и \( \Delta T \) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом \( C \) и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей \( n \), а не массой \( m \): Как найти \( C \)? Надо вычислить две разные величины: \( C_\mathrm{p} \) (при постоянном давлении) и \( C_\mathrm{v} \) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), \( Q=\Delta U+W \). Поэтому достаточно только выразить \( \Delta U \) через \( T \). Выполняемая работа \( W \) равна \( P\Delta\!V \), тогда при постоянном объеме \( W \) = 0. А изменение внутренней энергии идеального газа равно \( (3/2)nR\Delta T \) (см. главу 14), поэтому \( Q \) при постоянном объеме выражается следующей формулой: При постоянном давлении работа \( W \) равна \( P\Delta\!V \). А поскольку \( PV= nRT \), то \( W=P(V_1-V_0)=nR(T_1-T_0) \). Поэтому \( Q \) при постоянном давлении выражается следующей формулой: Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, \( Q=Cn\Delta T \), поэтому \( C=Q/n\Delta T \). Деля предыдущие две формулы на \( n\Delta T \), получаем: Теперь вы имеете молярные удельные теплоемкости идеального газа. Нужное вам отношение \( \gamma \) равно отношению этих двух формул: Связать давление и объем в любых двух точках адиабаты (см. предыдущий раздел об адиабатическом процессе) можно таким образом: Например, если сначала 1 л газа находился под давлением 1 атм, а после адиабатического изменения (когда обмена тепловой энергией нет), объем газа стал 2 л, то каким должно быть новое давление \( P_1 \)? Путем простой алгебраической операции деления на \( V_1^{5/3} \) оставляем в левой части равенства только \( P_1 \) и получаем: Подставив в эту формулу численные значения, получим: Итак, новое давление должно быть равно 0,314 атмосферы. Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении. Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит. Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически. Тепловая энергия, подаваемая нагревателем, обозначается как \( Q_{нг} \), а отправляемая в холодильник (см. предыдущий раздел) — как \( Q_{\mathrm{x}} \). Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы \( W \), выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу: Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть: Это значит, что для записи КПД достаточно использовать \( Q_{нг} \) и \( Q_{\mathrm{x}} \): Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·107 Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что \( W \) = 2,55·107 Дж и Это значит, что: Количество входящей тепловой энергии равно 3,27·107 Дж. А сколько тепловой энергии \( Q_{\mathrm{x}} \) остается неизрасходованной и отправляется в холодильник? Как известно: поэтому: Подставив в эту формулу численные значения, получим: Количество тепловой энергии, отправляемое в холодильник, равно 0,72·107 Дж. Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь. А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД. Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру \( T_{нг} \). А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру \( T_{х} \). Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах): А так как КПД теплового двигателя вычисляется по следующей формуле: то получается такая формула для вычисления КПД двигателя Карно: где температура выражается в кельвинах. В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. \( T_{х} \) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД. Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно: Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело: Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению. Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно. Странные явления вблизи абсолютного нуля Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям! (Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.) Глава 15. Тепловая энергия и работа: начала термодинамики fizi4ka.ru Здесь Единица измерения количества теплоты — Дж (Джоуль) или кал (калория). По сути тепловая энергия – это внутренняя энергия тела, значит потеря тепла – это уменьшение внутренней энергии тела, а нагревание – увеличение. Удельная теплоёмкость – это характеристика вещества, обозначающая его способность накапливать в себе внутреннюю (тепловую) энергию. Чем она меньше, тем легче вещество нагреть или охладить. Она не пропорциональна плотности, то есть более плотное вещество не обязательно будет нагреваться легче, чем менее плотное. Одно из веществ с большой теплоёмкостью – вода ( ru.solverbook.com К оглавлению... Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c. Тогда количество теплоты (энергии) необходимое для изменения температуры некоторого тела массой m можно рассчитать по формуле: При этом в этой формуле абсолютно не важно в каких единицах подставлена температура, так как нам важно не ее абсолютное значение, а изменение. Единица измерения удельной теплоемкости вещества: Дж/(кг∙К). Произведение массы тела на удельную теплоемкость вещества, из которого оно изготовлено называется теплоемкостью тела (т.е. просто теплоемкостью без слова «удельная»): Если в условии задачи сказано про теплоемкость тела, то количество теплоты, отданное или полученное этим телом, можно рассчитать по формуле: Итак, запомните: Напомним, что количество теплоты Q отданное каким–либо источником (нагревателем) рассчитывается по формуле: Q = Pt, где: P – мощность источника, t – время, в течение которого источник отдавал тепло. При решении задач не путайте время работа источника и температуру. К оглавлению... Фазой вещества называется однородная система, например, твердое тело, физические свойства которой во всех точках одинаковые. Между различными фазами вещества при обычных условиях существует четко выраженная граница (поверхность) раздела. При изменении внешних условий (температуры, давления, электрических и магнитных полей) вещество может переходить из одной фазы в другую. Такие процессы называются фазовыми превращениями (переходами). Процесс фазового перехода из жидкого состояния в газообразное (парообразование) или из твердого в жидкое (плавление) может происходить только при сообщении веществу некоторого количества теплоты. Обратные фазовые переходы (конденсация и кристаллизация, или отвердевание) сопровождаются выделением такого же количества теплоты. Количество теплоты, поступающее в систему или выделяющееся из нее, изменяет ее внутреннюю энергию. Это означает, что внутренняя энергия пара при 100°С больше, чем жидкости при той же температуре. Указанные фазовые переходы идут при постоянных температурах, которые называются соответственно температурой кипения и температурой плавления. Количество теплоты, необходимое для превращения жидкости в пар или выделяемое паром при конденсации, называется теплотой парообразования: где: r – удельная теплота парообразования. Единица измерения [r] = 1 Дж/кг. Физический смысл удельной теплоты парообразования: она равна количеству теплоты, необходимому для превращения в пар 1 кг жидкости, находящейся при температуре кипения. Превращение жидкости в пар не требует доведение жидкости до кипения. Вода может превратиться в пар и при комнатной температуре. Такой процесс называется испарением. Количество теплоты, необходимое для плавления тела или выделяемое при кристаллизации (отвердевании), называется теплотой плавления: где: λ – удельная теплота плавления. Единица измерения [λ] = 1 Дж/кг. Физический смысл удельной теплоты плавления: теплота, необходимая для плавления 1 кг вещества, находящегося при температуре плавления. Удельные теплоты парообразования и плавления называются также скрытыми теплотами, поскольку при фазовых переходах температура системы не меняется, несмотря на то, что теплота к ней подводится. Обратите внимание: что во время фазовых переходов температура системы не изменяется. А также на то, что сами фазовые переходы начинаются только после достижения необходимой температуры. Наиболее распространенным источником энергии для нужд человека является топливо – вещество, при сгорании которого выделяется некоторое количество теплоты. Количество теплоты, выделяемое при сгорании топлива массой m, называется теплотой сгорания топлива: где: q – удельная теплота сгорания (теплотворная способность, калорийность) топлива. Единица измерения [q] = 1 Дж/кг. Физический смысл удельной теплоты сгорания топлива: величина, показывающая, какое количество теплоты выделяется при полном сгорании 1 кг топлива. К оглавлению... В соответствии с законом сохранения энергии для замкнутой системы тел, в которой не происходит никаких превращений энергии, кроме теплообмена, количество теплоты, отдаваемое более нагретыми телами, равно количеству теплоты, получаемому более холодными. Теплообмен прекращается в состоянии термодинамического равновесия, т.е. когда температура всех тел системы становится одинаковой. Сформулируем уравнение теплового баланса: в замкнутой системе тел алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующими в теплообмене, равна нулю: При использовании такой формы записи уравнения теплового баланса, чтобы не сделать ошибку, запомните: когда Вы будете считать теплоту при нагревании или охлаждении тела, нужно из большей температуры вычитать меньшую, чтобы теплота всегда была положительной. Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то уравнение теплового баланса можно записать в виде: При использовании такой формы записи, нужно всегда от конечной температуры отнимать начальную. При таком подходе знак их разности сам «покажет» отдаёт тело теплоту или получает. Запомните, что тело поглощает теплоту если происходит: Тело отдает теплоту если происходит: Именно в этой теме, имеет смысл не решать задачи в общем виде, а сразу подставлять числа. При неупругих ударах механическая энергия частично или полностью переходит во внутреннюю энергию тел, то есть тела могут нагреваться и плавится. В общем случае изменение механической энергии равно выделяющемуся количеству теплоты. К оглавлению... Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно–кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно–кинетические модели для иллюстрации своих выводов. Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей. Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом. Если процесс протекает достаточно медленно (в пределе бесконечно медленно), то система в каждый момент времени оказывается близкой к равновесному состоянию. Процессы, состоящие из последовательности равновесных состояний, называются квазистатическими (или квазистационарными, еще одно название таких процессов - равновесные). В изобарном процессе работу идеального газа можно рассчитывать по формулам: Подчеркнем еще раз: работу газа по расширению можно считать по этим формулам только если давление постоянно. Согласно данной формуле, при расширении газ совершает положительную работу, а при сжатии – отрицательную (т.е. газ сопротивляется сжатию и над ним нужно совершать работу чтобы оно состоялось). Если давление нельзя считать постоянным, то работу газа находят, как площадь фигуры под графиком в координатах (p, V). Очевидно, что в изохорном процессе работа газа равна нулю. Ввиду того, что работа газа численно равна площади под графиком, становится понятно, что величина работы зависит от того, какой именно процесс происходил, ведь у каждого процесса свой график, а под ним своя площадь. Таким образом, работа зависит не только и не столько от начального и конечного состояний газа, сколько от процесса, с помощью которого конечное состояние было достигнуто. К оглавлению... Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно–кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема. Внутренняя энергия одноатомного идеального газа рассчитывается по формулам: Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния. Это значит, что изменение внутренней энергии не зависит от того, как система была переведена из одного состояния в другое (а зависит лишь от характеристик первоначального и конечного состояний) и всегда, в любых процессах для одноатомного идеального газа определяется выражением: Обратите внимание: эта формула верна только для одноатомного газа, зато она применима ко всем процессам (а не только к изобарному, как формула для работы). Как видно из формулы, если температура не изменялась, то внутренняя энергия остаётся постоянной. К оглавлению... Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, то есть изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы. Первый закон (начало) термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом: Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами. Однако, соотношение, выражающее первый закон термодинамики, чаще записывают в немного другой форме: Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами (такая формулировка более удобна и понятна, в таком виде совсем очевидно, что это просто закон сохранения энергии). Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких–либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии. Адиабатным (адиабатическим) называют процесс, в ходе которого система не обменивается теплотой с окружающей средой. При адиабатном процессе Q = 0. Поэтому: ΔU + A = 0, то есть: A = – ΔU. Газ совершает работу за счет уменьшения собственной внутренней энергии. К оглавлению... Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплотаQ, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const): Изобарный процесс (p = const): Изотермический процесс (T = const): Адиабатный процесс (Q = 0): Если в задаче явно не сказано, что газ одноатомный (или не назван один из инертных газов, например, гелий), то применять формулы из этого раздела нельзя. К оглавлению... Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т.д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. КПД тепловой машины может быть рассчитан по формуле: где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл: Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1). Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Цикл Карно состоит из двух изотерм и двух адиабат. КПД цикла Карно равен: К оглавлению... Первый закон термодинамики не устанавливает направление протекания тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым. Обратимыми процессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию. Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из–за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т.д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов. Первый закон термодинамики не может отличить обратимые процессы от необратимых. Он просто требует от термодинамического процесса определенного энергетического баланса и ничего не говорит о том, возможен такой процесс или нет. Направление самопроизвольно протекающих процессов устанавливает второй закон термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов. Английский физик У.Кельвин дал в 1851 году следующую формулировку второго закона: В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара. Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют «вечным двигателем второго рода». Как уже должно было стать понятно, второе начало термодинамики запрещает существование такого двигателя. Немецкий физик Р.Клаузиус дал другую формулировку второго закона термодинамики: Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой. Следует отметить, что обе формулировки второго закона термодинамики эквивалентны. К оглавлению... При решении различных нестандартных задач по термодинамике необходимо учитывать следующие замечания: К оглавлению... Задачи данной темы по праву считаются одними из самых сложных задач в термодинамике. Итак, для решения Вам придется, во-первых, перевести график процесса в p(V) – координаты. Во-вторых, надо рассчитать работу газа за цикл. Полезная работа равна площади фигуры внутри графика циклического процесса в координатах p(V). В-третьих, необходимо разобраться, где газ получает, а где отдает теплоту. Для этого вспомните первое начало термодинамики. Внутренняя энергия идеального газа зависит только от его температуры, а работа – от объема. Поэтому, газ получает теплоту, если: Газ отдает теплоту, если: Если один из параметров увеличивается, а другой уменьшается, для того, чтобы понять, отдает газ теплоту или получает ее, необходимо «в лоб» по первому началу термодинамики рассчитать теплоту и посмотреть на ее знак. Положительная теплота – газ ее получает. Отрицательная – отдает. Первый тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ получает теплоту в изохорных и изобарных процессах. Применяйте формулу: Обратите внимание, что в знаменателе стоит только теплота, полученная газом за один цикл, то есть теплота только в тех процессах, в которых газ получал ее. Второй тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ отдает теплоту в изохорных и изобарных процессах. Применяйте формулу: Обратите внимание, что в знаменателе стоит только теплота, отданная газом за один цикл, то есть теплота только в тех процессах, в которых газ отдавал ее. Третий тип задач. Газ получает теплоту не в удобных для расчета изохорных или изобарных процессах, в цикле есть изотермы или адиабаты, или вообще «никакие» процессы. Применяйте формулу: К оглавлению... Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов. Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно–кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, то есть к охлаждению жидкости (если нет подвода энергии от окружающих тел). Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость. В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, т.е. число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, это значит, что скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным. Насыщенный пар имеет максимальные: давление, концентрацию, плотность при данной температуре. Они зависят только от температуры насыщенного пара, но не от его объема. Это означает, что если бы мы сосуд закрыли не крышкой, а поршнем, и после того, как пар стал насыщенным, стали бы его сжимать, то давление, плотность и концентрация пара не изменились бы. Если быть более точным, то давление, плотность и концентрация на небольшое время увеличились бы, и пар стал бы перенасыщенным. Но сразу же часть пара превратилась бы в воду, и параметры пара стали бы прежними. Если поднять поршень, то пар перестанет быть насыщенным. Однако за счёт испарения через некоторое время снова станет насыщенным. Здесь следует учесть, что если воды на дне сосуда нет или её немного, то это испарение может оказаться недостаточным, чтобы пар снова стал насыщенным. Абсолютной влажностью ρ называют количество водяного пара, содержащегося в 1 м3 воздуха (т.е. просто плотность водяных паров; из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула): где: р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура. Единица измерения абсолютной влажности в СИ [ρ] = 1 кг/м3, хотя обычно используют 1 г/м3. Относительной влажностью φ называется отношение абсолютной влажности ρ к тому количеству водяного пара ρ0, которое необходимо для насыщения 1 м3 воздуха при данной температуре: Относительную влажность можно также определить как отношение давления водяного пара р к давлению насыщенного пара р0 при данной температуре: Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (то есть давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению. В частности, при нормальном атмосферном давлении вода кипит при температуре 100°С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. Важно знать, что температура кипения жидкости зависит от давления. В герметически закрытом сосуде жидкость кипеть не может, т.к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром. К оглавлению... Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может скачком переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах, и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Вследствие плотной упаковки молекул сжимаемость жидкостей, то есть изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах. Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (то есть увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔAвнеш, пропорциональную изменению ΔS площади поверхности. Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Ep поверхности жидкости пропорциональна ее площади: Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости на единицу при постоянной температуре. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2). Из механики известно, что educon.by 145. Молекулярная физика - раздел физики, изучающий строение и свойства вещества, исходя из молекулярно-кинетических представлений о его строении. 146. Основные положения молекулярно-кинетической теории: 1) Все тела состоят из атомов, молекул и ионов, имеющих в свою очередь сложное строение. 2) Атомы, молекулы и ионы находятся в непрерывном хаотическом движении, называемом тепловым. Скорость этого движения зависит от температуры. 3) Между атомами и молекулами существуют силы взаимного притяжения и отталкивания. 147. Экспериментальным подтверждением справедливости первых двух положений являются диффузия, броуновское движение, растворимость и др. Подтверждением справедливости третьего положения служит явление возникновения сил упругости при деформации тел. 148. Диффузия - это явление самопроизвольного проникновения молекул одного вещества в промежутки между молекулами другого вещества, происходящее в результате теплового движения. 149. Броуновское движение - это движение мельчайших макроскопических тел (пылинок, цветочной пыльцы, частичек туши и т.д.) под действием ударов со стороны молекул жидкости или газа. 150. Диаметр молекул имеет порядок 10-10 м, а масса - 10-26 кг. 151. Количество вещества - величина, равная числу структурных элементов (атомов, молекул, ионов), составляющих систему. где N - число частиц, NA - постоянная Авогадро, m – масса вещества, - молярная масса вещества. Единицей количества вещества является 1 моль. 152. 1 моль - это порция молекул, равная числу Авогадро. Более точное определение 1 моля: это порция молекул или других структурных единиц вещества, в которой содержится столько же молекул или других структурных единиц, сколько их содержится в 0,012 кг углерода. 153. Молярная масса - это масса одного моля данного вещества. Единицей молярной массы является кг/моль. 154. Относительная молекулярная масса – это величина численно равная отношению массы молекулы данного вещества к 1/12 массы изотопа атома углерода 6С12. Измеряется в углеродных единицах (у. ед) или атомных единицах (а.е.м.) 155. Число N молекул в теле массой m можно подсчитать по формуле: где - количество вещества, NА - число Авогадро, - молярная масса вещества, из которого состоит тело. 156. Идеальным называется газ, потенциальная энергия взаимодействия, между молекулами которого равна нулю. 157. Основное уравнение МКТ: где n - число молекул в единице объёма (концентрация), m - масса молекулы,- средний квадрат скорости. 158. Другой вид основного уравнения МКТ где p - давление, - средняя кинетическая энергия молекул. 159. Средняя квадратичная скорость молекул где – молярная масса вещества, m0 – масса молекулы, T – абсолютная температура. 160. Средняя кинетическая энергия поступательного движения молекулы идеального газа 161. Зависимость давления газа от концентрации молекул и температуры: 162. Температура - величина, характеризующая состояние термодинамического (теплового) равновесия макроскопической системы. 163. Абсолютный нуль температуры - это предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении. Можно сформулировать иначе: Абсолютный нуль температуры - это предельная температура, при которой прекращается поступательное движение молекул. 164. Абсолютная (термодинамическая) шкала - это шкала температур, в которой за начало отсчета принят абсолютный нуль. Единица температуры в этой шкале - кельвин (К), величина которого совпадает с градусом Цельсия. В шкале Цельсия абсолютный нуль равен -273,15С. Связь между абсолютной температурной шкалой и шкалой Цельсия выражается формулой 165. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона): где р - давление, V - объём, R=8,31 Дж/(мольК) - универсальная газовая постоянная, T - абсолютная температура, - молярная масса газа. Или где - плотность газа. 166. Уравнение Клапейрона или объединённый газовый закон: 167. Изотермическим называется процесс, протекающий при постоянной температуре. Если при этом масса газа не изменяется, то процесс подчиняется закону Бойля-Мариотта. Формулировка закона: Для данной массы газа произведение давления на объём при постоянной температуре есть величина постоянная. Или 168. Изобарным называется процесс, протекающий при постоянном давлении. Если масса газа не меняется, то процесс подчиняется закону Гей-Люссака: Для данной массы газа при постоянном давлении отношение объёма к абсолютной температуре есть величина постоянная. Или 169. Изохорным называется процесс, протекающий при постоянном объёме. Если масса газа постоянна, то процесс подчиняется закону Шарля: Для данной массы газа при постоянном объёме отношение давления к абсолютной температуре есть величина постоянная. Или 170. Давление смеси газов равно сумме парциальных давлений, созданных каждым газом. Этот закон известен под названием "закон Дальтона". 171. Термодинамика - это раздел физики, в котором рассматриваются тепловые явления с точки зрения происходящих в них преобразований энергии. 172. Внутренняя энергия - это сумма кинетической энергии хаотического движения молекул, потенциальной энергии их взаимодействия и внутримолекулярной энергии молекул, из которых состоит тело. 173. Внутреннюю энергию тел можно изменить двумя способами: теплообмен и совершение работы. Признаком изменения внутренней энергии тела является изменение его температуры и (или) агрегатного состояния. 174. Внутренняя энергия одноатомного, идеального газа определяется по формуле: 175. Изменение внутренней энергии одноатомного газа можно подсчитать по формуле: где m - масса газа, - молярная масса газа. 176. Теплообмен бывает трёх видов: лучеиспускание, конвекция, теплопередача. Лучеиспускание - это теплообмен с помощью электромагнитных волн теплового диапазона. Конвекция - это теплообмен, осуществляемый при перемешивании жидкостей или газов, имеющих разную температуру, Теплопередача -это форма передачи энергии, при которой осуществляется непосредственный обмен энергией между хаотически движущимися молекулами тел при их тепловом контакте. 177. Количество теплоты - это энергия, которую тело получает или отдаёт при теплообмене. 178. Теплоёмкость тела - это величина равная количеству теплоты, которое надо передать телу для изменения его температуры на 1 кельвин. Теплоёмкость тела измеряется в Дж/К. Количество теплоты, которое надо сообщить телу с теплоёмкостью С вычисляется по формуле 179. Удельная теплоёмкость - это величина численно равная количеству теплоты, которую надо сообщить веществу массой 1 кг для изменения его температуры на 1 кельвин. Удельная теплоёмкость измеряется в Дж/(кгК). Теплоёмкость тела связана с удельной теплоёмкостью вещества, из которого оно изготовлено, формулой 180. Закон сохранения энергии в тепловых процессах (первый закон термодинамики): количество теплоты, переданное телу, идёт на увеличение его внутренней энергии и на совершение работы против внешних сил. 181. Применение первого закона термодинамики к изопроцессам. 1) Изотермический (Т=const) т.к. U=0, т.е. количество теплоты, переданное системе, идёт на совершение работы против внешних сил; 2) Изобарный (p=const) т.е. количество теплоты, переданное системе, идёт на совершение работы против внешних сил и на изменение её внутренней энергии; 3) Изохорный (V=const) т.е. количество теплоты, переданное системе, идёт на изменение её внутренней энергии. 4) Адиабатным называется процесс, протекающий без теплообмена с окружающей средой (Q=0). Закон сохранения энергии для него имеет вид: т.е. работа против внешних сил совершается за счёт убыли внутренней энергии. 182. Работа расширения газа при постоянном давлении вычисляется по формуле: где V2 и V1 - конечный и начальный объёмы газа, р - давление. Т.к. то где T2 - температура газа в конечном состоянии, T1 - температура газа в начальном состоянии, - молярная масса, R - универсальная газовая постоянная. 183. Тепловой двигатель (тепловая машина) - это устройство, совершающее работу за счёт уменьшения внутренней энергии рабочего тела. 184. Любая тепловая машина состоит из трёх частей: нагревателя, холодильника и рабочего тела. 185. Тепловой коэффициент полезного действия тепловой машины равен: где Q1 - количество теплоты, полученной от нагревателя, Q2 - количество теплоты, отданной холодильнику, A ‑ механическая работа. 186. Формула Карно для идеальной тепловой машины: где Т1 - температура нагревателя, Т2 - температура холодильника, - КПД. 187. Плавление - это процесс перехода вещества из твёрдого состояния в жидкое при температуре плавления. 188. Процесс превращения жидкости в твёрдое кристаллическое состояние называется кристаллизацией. 189. Удельная теплота плавления - это количество теплоты, необходимое для превращения 1 кг твёрдого кристаллического вещества из твёрдого состояния в жидкое, при температуре плавления. Удельная теплота плавления измеряется в Дж/кг . 190. Парообразование - это процесс перехода вещества из твёрдого или жидкого состояния в газообразное. 191. Испарение - это процесс парообразования, происходящий с открытой поверхности жидкости или твёрдого тела. 192. Сублимация (возгонка) – это переход твёрдого вещества в газообразное, минуя жидкое состояние. 193. Кипение - это процесс парообразования, происходящий не только с открытой поверхности жидкости, но и по всему её объёму внутрь пузырьков газа, растворённого в жидкости. Для каждой жидкости существует своя температура кипения. Жидкость кипит при такой температуре, при которой давление её насыщенных паров равно атмосферному давлению. 194. Пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным. 195.Точка росы - температура, при которой пар переходит в состояние насыщения. 196. Процесс перехода вещества из газообразного состояния в жидкое, называется конденсацией. 197. Количество теплоты, которое необходимо для превращения единицы массы жидкости в пар, называется удельной теплотой парообразования и конденсации Удельная теплота парообразования измеряется в Дж/кг. 198. Абсолютная влажность - это парциальное давление (плотность) водяных паров в атмосфере. 199. Относительная влажность - это величина равная отношению абсолютной влажности к давлению (плотности) насыщенного пара при данной температуре. studfiles.net Изменить внутреннюю энергию газа в цилиндре можно не только совершая работу, но и нагревая газ (рис. 43). Если закрепить поршень, то объем газа не будет изменяться, но температура, а следовательно, и внутренняя энергия будут возрастать. Энергию, переданную телу в результате теплообмена, называют количеством теплоты. Количеством теплоты называют также энергию, которую тело отдает в процессе теплообмена. Молекулярная картина теплообмена. При теплообмене на границе между телами происходит взаимодействие медленно движущихся молекул холодного тела с более быстро движущимися молекулами горячего тела. В результате кинетические энергии молекул выравниваются и скорости молекул холодного тела увеличиваются, а горячего уменьшаются. При теплообмене не происходит превращения энергии из одной формы в другую: часть внутренней энергии горячего тела передается холодному телу. Количество теплоты и теплоемкость. Из курса физики VII класса известно, что для нагревания тела массой m от температуры t1 до температуры t2 необходимо сообщить ему количество теплоты Q = cm(t2 – t1) = cmΔt. (4.5) При остывании тела его извечная температура t2 меньше начальной t1 и количество теплоты, отдаваемое телом, отрицательно.Коэффициент c в формуле (4.5) называют удельной теплоемкостью. Удельная теплоемкость – это количество теплоты, которое получает или отдает 1 кг вещества при изменении его температуры на 1 К. Удельную теплоемкость выражают в джоулях, деленных на килограмм, умноженный на кельвин. Различным телам требуется неодинаковое количество энергии для увеличения температуры на 1 К. Так, удельная теплоемкость воды 4190 Дж/(кг · К), а меди 380 Дж/(кг · К). Удельная теплоемкость зависит не только от свойств вещества, но и от того, при каком процессе осуществляется теплопередача. Если нагревать газ при постоянном давлении, то он будет расширяться и совершать работу. Для нагревания газа на 1°C при постоянном давлении ему нужно будет передать большее количество теплоты, чем для нагревания его при постоянном объеме. Жидкие и твердые тела расширяются при нагревании незначительно, и их удельные теплоемкости при постоянном объеме и постоянном давлении мало различаются. Удельная теплота парообразования. Для превращения жидкости в пар необходима передача ей определенного количества теплоты. Температура жидкости при этом превращении не меняется. Превращение жидкости в пар при постоянной температуре не ведет к увеличению кинетической энергии молекул, но сопровождается увеличением их потенциальной энергии. Ведь среднее расстояние между молекулами газа во много раз больше, чем между молекулами жидкости. Кроме того, увеличение объема при переходе вещества из жидкого состояния в газообразное требует совершения работы против сил внешнего давления. Количество теплоты, необходимое для превращения при настоянной температуре 1 кг жидкости в пар, называют удельной теплотой парообразования. Обозначают эту величину буквой r и выражают в джоулях на килограмм. Очень велика удельная теплота парообразования воды: 2,256 · 106 Дж/кг при температуре 100°C. У других жидкостей (спирт, эфир, ртуть, керосин и др.) удельная теплота парообразования меньше в 3-10 раз. Для превращения в пар жидкости массой m требуется количество теплоты, равное: Qn = rm (4.6) При конденсации пара происходит выделение такого же количества теплоты Qk = –rm. (4.7) Удельная теплота плавления. При плавлении кристаллического тела вся подводимая к нему теплота идет на увеличение потенциальной энергии молекул. Кинетическая энергия молекул не меняется, так как плавление происходит при постоянной температуре. Количество теплоты λ (лямбда), необходимое для превращения 1 кг кристаллического вещества при температуре плавления в жидкость той же температуры, называют удельной теплотой плавления. При кристаллизации 1 кг вещества выделяется точно такое же количество теплоты. Удельная теплота плавления льда довольно велика: 3,4 · 105 Дж/кг. Для того чтобы расплавить кристаллическое тело массой m, необходимо количество теплоты, равное: Qпл = λm. (4.8) Количество теплоты, выделяемое при кристаллизации тела, равно: Qкр = – λm. (4.9) 1. Что называют количеством теплоты? 2. От чего зависит удельная теплоемкость веществ? 3. Что называют удельной теплотой парообразования? 4. Что называют удельной теплотой плавления? 5. В каких случаях количество переданной теплоты отрицательно? phscs.ru Количество теплоты. Основные понятия Количество теплоты Раздел молекулярной физики, который изучает передачу энергии, закономерности превращения одних видов энергии в другие. В отличие от молекулярно-кинетической теории, в термодинамике не учитывается внутреннее строение веществ и микропараметры. Это совокупность тел, которые обмениваются энергией (в форме работы или теплоты) друг с другом или с окружающей средой. Например, вода в чайнике остывает, происходит обмен теплотой воды с чайником и чайника с окружающей средой. Цилиндр с газом под поршнем: поршень выполняет работу, в результате чего, газ получает энергию, и изменяются его макропараметры. Это энергия, которую получает или отдает система в процессе теплообмена. Обозначается символом Q, измеряется, как любая энергия, в Джоулях. В результате различных процессов теплообмена энергия, которая передается, определяется по-своему. Нагревание и охлаждение Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле Удельная теплоемкость вещества с измеряется количеством теплоты, которое необходимо для нагревания единицы массы данного вещества на 1К. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость - известная, уже вычисленная для всех веществ величина, значение смотреть в физических таблицах. Теплоемкость вещества С - это количество теплоты, которое необходимо для нагревания тела без учета его массы на 1К. Плавление и кристаллизация Плавление - переход вещества из твердого состояния в жидкое. Обратный переход называется кристаллизацией. Энергия, которая тратится на разрушение кристаллической решетки вещества, определяется по формуле Удельная теплота плавления известная для каждого вещества величина, значение смотреть в физических таблицах. Парообразование (испарение или кипение) и конденсация Парообразование - это переход вещества из жидкого (твердого) состояния в газообразное. Обратный процесс называется конденсацией. Удельная теплота парообразования известная для каждого вещества величина, значение смотреть в физических таблицах. Горение Количество теплоты, которое выделяется при сгорании вещества Удельная теплота сгорания известная для каждого вещества величина, значение смотреть в физических таблицах. Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса. Алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующим в теплообмене, равна нулю: Q1+Q2+...+Qn=0 fizmat.by m — масса; μ — молярная масса вещества; N — число молекул; NA = 6,02·1023 моль-1 — число Авогадро p — давление идеального газа; m — масса одной молекулы; n = N/V — концентрация молекул; V — объем газа; N — число молекул; k = 1,38·10-23 Дж/К — постоянная Больцмана; R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная; T = t+273 — абсолютная температура; t — температура по шкале Цельсия. n — концентрация молекул; k — постоянная Больцмана; T — абсолютная температура. p — давление; V — объем газа. p0 — давление газа при 0 °С; α = 1/273 °C-1 — температурный коэффициент давления. V0 — объем газа при 0 °С. pi — парциальное давление i-й компоненты смеси газов. ν — количество вещества; R = 8,31 Дж/(моль·К) — универсальная газовая постоянная; T — абсолютная температура. при изменении объема на бесконечно малую величину dV p — давление газа. При изменении объема от V1 до V2 ΔQ — количество подведенной теплоты; ΔA — работа, совершаемая веществом; ΔU — изменение внутренней энергии вещества. ΔQ — количество переданной системе теплоты на участке процесса; ΔT — изменение температуры на этом участке процесса. fizikazadachi.ruМолекулярная физика. Тепловые явления. Тепловая мощность физика формула
Глава 15. Тепловая энергия и работа: начала термодинамики – FIZI4KA

Стремимся к тепловому равновесию: нулевое начало термодинамики
Сохраняем энергию: первое начало термодинамики

Применяем закон сохранения энергии




Изучаем изобарические, изохорические, изотермические и адиабатические процессы
Постоянное давление: изобарический процесс





Постоянный объем: изохорический процесс

Постоянная температура: изотермический процесс







Постоянная энергия: адиабатический процесс




Вычисляем удельную теплоемкость









Передаем тепловую энергию: второе начало термодинамики
Заставим тепловую энергию работать: тепловые двигатели

Оцениваем эффективность работы: КПД теплового двигателя


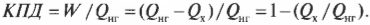





Как сказал Карно: нельзя все тепло превратить в работу
Построение двигателя Карно



Используем формулу Карно


Охлаждаемся: третье (и абсолютно последнее) начало термодинамики
Формула количества теплоты
![Rendered by QuickLaTeX.com \[ Q = c m \Delta T \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-21d08871960fd1d6601e7bcf690425c3_l3.png)
 – количество теплоты,
– количество теплоты,  – удельная теплоёмкость вещества, из которого состоит тело,
– удельная теплоёмкость вещества, из которого состоит тело, 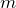 – масса тела,
– масса тела,  – разность температур.
– разность температур.

 Дж/(кг * К)).
Дж/(кг * К)).Примеры решения задач по теме «Количество теплоты»

Понравился сайт? Расскажи друзьям!
Термодинамика - Физика - Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Теплоемкость вещества
Фазовые превращения
Уравнение теплового баланса
Взаимные превращения механической и внутренней энергии
Работа идеального газа
Внутренняя энергия
Первый закон термодинамики
Первое начало термодинамики и изопроцессы
Циклы. Тепловые машины
Второе начало (второй закон) термодинамики
Сложные задачи по термодинамике
Расчет КПД циклов по графику
Свойства паров. Влажность
Поверхностное натяжение
Молекулярная физика. Тепловые явления
Количество теплоты | Физика
 Процесс передачи энергии от одного тела к другому без совершения работы называют теплообменом или теплопередачей.
Процесс передачи энергии от одного тела к другому без совершения работы называют теплообменом или теплопередачей.Количество теплоты: нагревание, охлаждение, плавление, кристаллизация, парообразование, конденсация, горение. Термодинамическая система
Тестирование онлайн
Термодинамика
Термодинамическая система
Количество теплоты









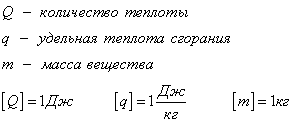
Молекулярная физика - Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества

1.2 Основное уравнение молекулярно-кинетической теории идеального газа

 — среднее значение квадрата скорости молекул.
— среднее значение квадрата скорости молекул.1.3 Средняя квадратичная скорость молекул идеального газа

1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

1.6 Закон Бойля-Мариотта

1.7 Закон Шарля

1.8 Закон Гей-Люссака

1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа

2.2 Элементарная работа, совершаемая газом,


2.3 Первый закон термодинамики

2.4 Теплоемкость идеального газа

интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: