Иметь представление о мощности при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия. Знать зависимости для определения мощности при поступательном и вращательном движениях, КПД. Уметь рассчитать мощность с учетом потерь на трение и сил инерции. Мощность Для характеристики работоспособности и быстроты совершения работы введено понятие мощности. Единицы измерения мощности: ватты, киловатты, Мощность при поступательном движении (рис. 16.1) Учитывая, что S/t = vcp, получим где F — модуль силы, действующей на тело; vср — средняя скорость движения тела. Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости. Тело движется по дуге радиуса r из точки М1 в точку M2 Работа силы: где Мвр — вращающий момент. Учитывая, что где ωcp — средняя угловая скорость. Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость. Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент. Мощностью силы. Коэффициент полезного действия. Работа и мощность коэффициент полезного действия
Тема 1.14. Работа и мощность. Коэффициент полезного действия.
 Мощность — работа, выполненная в единицу времени:
Мощность — работа, выполненная в единицу времени:

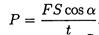

 Мощность при вращении (рис. 16.2)
Мощность при вращении (рис. 16.2)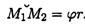
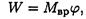


 получим
получим 
Похожие статьи:
poznayka.org
Конспект "Механическая работа, мощность и КПД"
Механическая работа, мощность и КПД механизма
1. Механическая работа (или работа силы над телом) – физическая величина, равная по модулю произведению силы на путь, пройденный телом вдоль направления этой силы. Если вектор силы перпендикулярен направлению движения тела, то совершаемая этой силой работа равна нулю; если вектор силы сонаправлен с направлением движения тела, то работу силы считают положительной; если вектор силы противоположен направлению движения тела, то работу силы считают отрицательной.
- В случае, когда точка приложения силы перемещается в направлении действия силы, механическая работа А равна произведению модуля F силы на путь s, пройденный точкой приложения силы: А = Fs.
- Единица работы в СИ 1 Джоуль (Дж) = 1 Нм.
- «Золотое правило» механики с использованием понятия работы: никакой простой механизм не дает выигрыша в работе.
Таблица «Механическая работа, мощность и КПД»

2. Коэффициент полезного действия (КПД) – физическая величина, равная отношению полезной работы к полной совершённой работе. КПД показывает долю полезной работы от полной и, как и все доли, всегда имеет положительный знак и не имеет «своей» единицы для измерения. Значение КПД обычно выражают в процентах, которое нужно переводить в десятичную дробь для дальнейших вычислений.
- Коэффициентом полезного действия (КПД) механизма называют отношение полезной работы Апол к совершенной Асов, выраженное в процентах: η = Апол/Асов · 100%.
- КПД любого реального механизма меньше 100 % (из-за трения и из-за того, что сами механизмы и их части имеют некоторую массу).
3. Мощность действия – физическая величина, равная отношению механической работы ко времени, за которое она была совершена. Мощность характеризует быстроту (скорость) совершения работы. Мощность принято вычислять только для тех действий, в которых механическая работа положительна.
- Мощностью N называют отношение совершенной работы А к промежутку времени t, за который эта работа совершена: N = A/t
- Единица мощности в СИ 1 ватт (Вт) = 1 Дж/с.
- Мощность можно выразить через силу и скорость с помощью формулы N = Fv.
Схема «Механическая работа. Мощность»

Конспект урока «Механическая работа и энергия».
Следующая тема: «Простые механизмы. Блоки»
Механическая работа, мощность и КПД
4.5 (90%) 2 votesuchitel.pro
Коэффициент полезного действия
Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений. Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.
Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом полезного действия (КПД):

Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:

Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери.
Чем выше КПД, тем совершеннее машина.
Примеры решения задач
 Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.
Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.
Решение
1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.
Полезная мощность определяется по формуле
Р = Fv cos α.
В данном случае α = 0; груз движется поступательно.
1. Скорость подъема груза

2. Необходимое усилие равно весу груза (равномерный подъем).
4. Полезная мощность Р = 3000 • 4 = 12 000 Вт.
5. Полная мощность. затрачиваемая мотором,

Пример 2. Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления воды движению судна. КПД машины 0,4.

Решение
1. Определяем полезную мощность, используемую на движение с заданной скоростью:
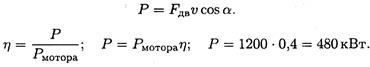
2. По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды:
Fдв = Fcопр.
3. Скорость движения судна v = 36 * 1000/3600 = 10 м/с
4. Сила сопротивления воды

Сила сопротивления воды движению судна
Fcопр. = 48 кН
 Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.
Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.
Решение
1. Резание осуществляется за счет трения между точильным камнем и обрабатываемой деталью:
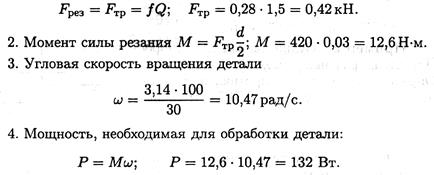
 Пример 4. Для того чтобы поднять волоком по наклонной плоскости на высоту H = 10 м станину массой т == 500 кг, воспользовались электрической лебедкой (рис. 1.64). Вращающий момент на выходном барабане лебедки М = 250 Н-м. Барабан равномерно вращается с частотой п = 30 об/мин. Для подъема станины лебедка работала в течение t = 2 мин. Определить коэффициент полезного действия наклонной плоскости.
Пример 4. Для того чтобы поднять волоком по наклонной плоскости на высоту H = 10 м станину массой т == 500 кг, воспользовались электрической лебедкой (рис. 1.64). Вращающий момент на выходном барабане лебедки М = 250 Н-м. Барабан равномерно вращается с частотой п = 30 об/мин. Для подъема станины лебедка работала в течение t = 2 мин. Определить коэффициент полезного действия наклонной плоскости.
Решение
Как известно,

где Ап.с. — полезная работа; Адв — работа движущих сил.
В рассматриваемом примере полезная работа — работа силы тяжести
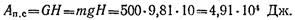
Вычислим работу движущих сил, т. е. работу вращающего момента на выходном валу лебедки:

Угол поворота барабана лебедки определяется по уравнению равномерного вращения:

где
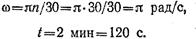
Тогда

Подставив в выражение работы движущих сил числовые значения вращающего момента М и угла поворота φ, получим:

Коэффициент полезного действия наклонной плоскости составит
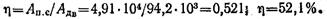
Контрольные вопросы и задания
1. Запишите формулы для расчета работы при поступательном и вращательном движениях.
2. Вагон массой 1000 кг перемещают по горизонтальному пути на 5 м, коэффициент трения 0,15. Определите работу силы тяжести.
3. Колодочным тормозом останавливают барабан после отключения двигателя (рис. 16.6). Определите работу торможения за 3 оборота, если сила прижатия колодок к барабану 1 кН, коэффициент трения 0,3.
4. Натяжение ветвей ременной передачи S1 = 700 Н, S2 = 300 Н (рис. 16.7). Определите вращающий момент передачи.
5. Запишите формулы для расчета мощности при поступательном и вращательном движениях.
6. Определите мощность, необходимую для подъема груза весом 0,5 кН на высоту 10 м за 1 мин.
7. Определите общий КПД механизма, если при мощности двигателя 12,5 кВт и общей силе сопротивления движению 2 кН скорость движения 5 м/с.
8. Ответьте на вопросы тестового задания.
 |
Тема 1.14. Динамика. Работа и мощность
 |
Похожие статьи:
poznayka.org
Механическая работа, мощность, КПД. Энергия.
Работа, совершаемая переменной силой на пути: A =  Работа силы тяжести вблизи поверхности Земли: A =mgh;
Работа силы упругости: A =kx2/2.
Работа силы трения: A = - Ft Δr.
Мгновенная мощность:
Работа силы тяжести вблизи поверхности Земли: A =mgh;
Работа силы упругости: A =kx2/2.
Работа силы трения: A = - Ft Δr.
Мгновенная мощность:  N =Fv =Frv = Fvcos α
Коэффициент полезного действия (КПД): N =Fv =Frv = Fvcos α
Коэффициент полезного действия (КПД): 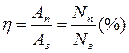 An, A3, Nn, N3 – соответственно полезные и затраченные работа и мощность An, A3, Nn, N3 – соответственно полезные и затраченные работа и мощность
|
Кинетическая энергия:  |
Связь между консервативной силой, действующей на тело в данной точке, и потенциальной энергией частицы:   = - grad Wп ;
Потенциальная энергия частицы в поле центральных сил:
Wп(r) = ΔA = - = - grad Wп ;
Потенциальная энергия частицы в поле центральных сил:
Wп(r) = ΔA = - 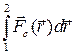 ,
предположив Wп(∞) = 0,
получим Wп(r) = ,
предположив Wп(∞) = 0,
получим Wп(r) = 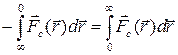 .
Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии r: .
Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии r:  Потенциальная энергия тела в поле силы тяжести Земли:
Потенциальная энергия тела в поле силы тяжести Земли:  где r = R +h - расстояние от центра Земли до центра масс тела.
Потенциальная энергия тела в однородном поле силы тяжести (h<<R):
Wп = mgh, где g – ускорение свободного падения.
Потенциальная энергия упруго деформированного тела:
где r = R +h - расстояние от центра Земли до центра масс тела.
Потенциальная энергия тела в однородном поле силы тяжести (h<<R):
Wп = mgh, где g – ускорение свободного падения.
Потенциальная энергия упруго деформированного тела: 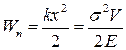 где k - коэффициент жесткости, x – смещение;
σ – нормальное напряжение; E – модуль Юнга; V – объем.
где k - коэффициент жесткости, x – смещение;
σ – нормальное напряжение; E – модуль Юнга; V – объем.
|
ЗАДАНИЕ 6. ЗАКОНЫ СОХРАНЕНИЯ ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
Закон сохранения момента импульса. Работа при вращении тела. Кинетическая энергия вращательного движения.
Закон сохранения момента импульса для замкнутой системы
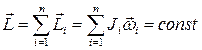 |
| Работа при вращении тела: ΔA = MzΔφ, где Δφ - угол поворота тела; Mz - момент силы относительно оси |
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
 ,
где J– момент инерции тела относительно оси, ω - его угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения: ,
где J– момент инерции тела относительно оси, ω - его угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
 где m– масса тела; vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
где m– масса тела; vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
|
Аналогия между формулами поступательного и вращательного движения.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КОНТРОЛЬНАЯ РАБОТА № 1
Пример 1.Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = А + В t + С t3, где А = 4 м, В = 2 м/с, С = - 0,5 м/с2. Для момента времени t1 = 2 с определить: 1) координату х1 точки; 2) мгновенную скорость V1; 3) мгновенное ускорение а1.
Дано:
х = А + В t + С t3
А = 4 м
В = 2 м/с
С = - 0,5 м/с2.
t1 = 2 с
_____________
х1-? V1-? а1-?
Решение. Найдем координату точки, для которой известно кинематическое уравнение движения, подставив в уравнение движения вместо t заданное значение t1:
х1 = А + В t1 + С t13; х1 = 4 м.
Мгновенную скорость V в произвольный момент времени t найдем, продифференцировав координату х по времени:
V = 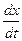 = B + 3Ct2.
= B + 3Ct2.
Тогда в заданный момент времени мгновенная скорость:
V1 = B + 3Ct21;
Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты по времени:
a =  = 6Ct, т.е. a1 = 6Ct1
= 6Ct, т.е. a1 = 6Ct1
Вычисления:
Скорость V1 = - 4 м/с. Знак минус указывает на то, что в момент времени t1 = 2 с точка движется в отрицательном направлении координатной оси.
Мгновенное ускорение в заданный момент времени равно:
a1 = - 6 м/c2 ,
Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси.
Ответ: V1 = - 4 м/с, a1 = - 6 м/c2
Пример 2.Тело вращается вокруг неподвижной оси по закону, выражаемому формулой φ = 10 + 20 t - 2 t2 (рис. 1). Найдите по величине и направлению полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t1 = 4 с.

Условие:
φ=10+20t-2t2;
R=0,1 м;
t1=4 c;
a - ? α - ?
Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки определяется геометрической суммой тангенциального и нормального ускорения:
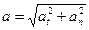 (1)
(1)
Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
а t= εR; (2)
an = ω2R, (3)
где ω - угловая скорость тела; ε - его угловое ускорение; R - расстояние от оси вращения.
Подставляя выражения аt и аn в формулу (1) находим:
a = R  . (4)
. (4)
Угловая скорость вращающегося тела равна первой производной от угла поворота по времени
ω = 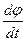 = 20 – 4t.
= 20 – 4t.
В момент времени t = 4 с угловая скорость ω = 4 с-1.
Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени:
ε =  = - 4 c-2.
= - 4 c-2.
Подставляя найденные и заданные значения в формулу (4) получим:
a = 1,65 м/c2.
Направление полного ускорения можно определить, если найти углы, которые векторы ускорения составляют с касательной к траектории или нормалью к ней:
cos α = 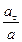 . (5)
. (5)
Вычисления:
По формулам (2) и (3) найдем значения аt и an:
at = - 0,4 /c2; an = 1,6 /c2 .
Подставив эти значения и значения полного ускорения в формулу (5), получим:
cos α = 0,242; α = 760.
Ответ: a = 1,65 м/c2, α = 760
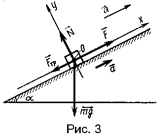 Пример 3. Автомобиль массой m = 1000 кг движется вверх по наклонной плоскости с уклоном 0,1, развивая на пути S = 200 м скорость vк = 54 км/ч. Коэффициент трения μ = 0,05. Определить силу тяги двигателя
Пример 3. Автомобиль массой m = 1000 кг движется вверх по наклонной плоскости с уклоном 0,1, развивая на пути S = 200 м скорость vк = 54 км/ч. Коэффициент трения μ = 0,05. Определить силу тяги двигателя
Условие:
m =1000 кг;
S=200 м;
sina =0,1
μ=0,05;
v0 =0;
vк =54км/ч = 15м/с;
F - ?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3).
На автомобиль действует четыре силы: сила тяжести FТ=mg, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
 .
.
Это уравнение в проекциях на оси координат
на ось х : ma = F – mg sina - FTP,
на ось у : 0 = N – mg cosa,
FTP = μ N.
соsa= 
Выразим из этих уравнений силу тяги F
F = mg sina + μmg cosa + ma.
Ускорение на этом участке равно:
a = (vk2 - v02)/(2s) = vk2/(2s).
Найдем силу тяги двигателя на этом участке:
F = mg sinα + μmg cosα +  = m(g sin α + μg cos α +
= m(g sin α + μg cos α +  )
)
Вычисления:
F = 1000(0.98+0,50+0,56) = 2043( Н)
Ответ: F =2043( Н)
Пример 4.На горизонтальной платформе шахтной клети стоит человек массой m = 60 кг. Определить силу давления человека на платформу: 1) при ее подъеме с ускорением
а1 = 3 м/с2; 2) при равномерном подъеме и спуске; 3) при спуске с ускорением а3 = 9,8 м/с2.
 Условие:
Условие:
m=60 кг;
а1=3 м/с2;
v2=const, a2=0;
а3=9,8 м/с;
F1- ? F2 - ? F3 - ?
Решение. На человека, стоящего на платформе шахтной клети действуют две силы: сила тяжести mg и сила реакции опоры N. Согласно второму закону Ньютона:
 .(1)
.(1)
Согласно третьему закону Ньютона сила давления человека на платформу равна силе реакции опоры:
 NN = F (2)
NN = F (2)
1. Согласно рис. 2 запишем уравнение (1) в проекции на ось У
ma1 = N1 – mg
Учитывая (2) получим
F1 = N1 = m (g + a1),
2. При равномерном движении шахтной клети а2= 0 и, следовательно, сила давления человeка на платформу равна силе тяжести: F2 = N2 = mg.
3. При спуске платформы с ускорением, направленным вниз уравнение движения платформы имеет вид ma3 = mg – N3.
Откуда сила давления человека на платформу: F3 = N3 = =m(g – a3).
Учитывая, что а3 = g имеем F3 = 0 .
Следоватeльно, человек не давит на платформу.
Вычисления:
F1 = 783 H, F2 =60·9,81=588,6 (Н), F3 = 0.
Ответ: F1 = 783 H, F2 =588,6 (Н), F3 = 0.
Пример 5 .Каким был бы период обращения ИСЗ на круговой орбите, если бы он был удален от поверхности Земли на расстояние, равное земному радиусу (R = 6400 км).
Условие: h = R = 6370 км;
Т - ?
Решение. Период обращения ИСЗ по круговой орбите
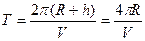 .
.
Для определения скорости спутника учтем, что при его движении по круговой орбите на спутник действует только сила притяжения Земли Ft, сообщающая ему нормальное ускорение:
Ft = Fn; 
где G – гравитационная постоянная, m – масса спутника, M – масса Земли.
Отсюда скорость спутника равна

Учитывая, что
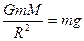
где g – ускорение силы тяжести на поверхности Земли, получаем

Подставляя это значение скорости в формулу периода, найдем, что

Вычисление: Т =  14360 (с) = 3 ч 59 мин
14360 (с) = 3 ч 59 мин
Ответ: Т = 3 ч 59 мин.
Пример 6.Стальная прoвoлока сечением S= 3 мм2 под действием растягивающей силы, равной F = 4 . 104 Н имеет длинy L1 = 2 м. Определить абсолютное удлинение проволоки при увеличении растягивающей силы на F1 = 104 Н. Модуль Юнга стали Е =2 . 1011 Па.
Условие:
Е = 2·1011 Па;
S= 3 мм2 =3·10-6 м2;
L1 = 2 м;
F = 4·104 Н;
F1=1,0·104 Н;
ΔL2 - ?
Решение. Для того чтобы найти абсолютное удлинение проволоки при увеличенной растягивающей силе, необходимо узнать ее первоначальную длину L. Из закона Гука
F = εE = E(L1 – L)S/L
находим L = EL1S/(F +ES).
При увеличении растягивающей силы на величину F1
F + F1 = EΔL2S/L.
Откуда ΔL2 = (F + F1)L/ES.
Заменив L выражением, записанным выше, получаем
ΔL2 = (F + F1)L1/(F + ES).
Проверка размерности:  .
.
Вычисление:ΔL2 = (4·104+1,0·104)2/(4·104+ 2·10113·10-6)=0,16(м)
Ответ: ΔL2 = 0, 16 м.
Пример 7.Маховик, массу которого m = 5 кг можно считать распределенной по ободу радиуса r = 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр с частотой n = 720 мин-1. При торможении маховик останавливается через Δt = 20 с. Определить тормозящий момент М и число оборотов N, которое сделает маховик до полной остановки.
Условие:
m = 5 кг
r = 20см =0,20 м
n =720 мин-1 = 12 с-1
Δt =20 с
М - ? N - ?
Решение. Если тормозящий момент постоянен, то движение маховика равнозамедленное, и основное уравнение динамики вращательного движения можно записать в виде:
 (1)
(1)
где  - изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент.
- изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент.
Число оборотов N может быть найдено как кинематически, так и по изменению кинетической энергии, равному работе совершаемой тормозящей силой.
Векторному уравнению (1) соответствует скалярное уравнение
J∆ω = M∆t, (2)
где ∆ω, M - модули соответствующих векторов.
Из условия задачи следует, что
∆ω = |ω – ω0|= ω0 =2πn (3)
Поскольку масса маховика распределена по ободу, момент инерции
J = mr2 (4)
Подставляя выражения (2), (3) в (1) получим
mr22πn = M∆t.
Откуда M = 2πnmr2/Δt .
Векторы  направлены в сторону противоположную вектору
направлены в сторону противоположную вектору 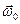 .
.
Угловое перемещение, пройденное маховиком до остановки
φ = ω0∆t – ε∆t2/2. (5)
Учитывая, что ω = ωo - ε∆t = 0 преобразуем выражение (6)
φ = ω0∆t/2.
Так как φ = 2πN, ω =2πn, где N - число оборотов, которое делает маховик до полной остановки, окончательно получим
N = nt/2
Проверяем размерность: 
Вычисления: М = 2·3,14·5·0,04/20 = 0,75 (Дж)
N = 12·20/2=120 (об)
Ответ: М = 0,75 Дж , N = 120 об.
 Пример 8.Автомобиль массой m = 2000 кг движется вверх по наклонной плоскости под углом α = 150 , развивая на пути S = 100 м скорость vк = 36 км/ч. Коэффициент трения μ = 0,05. Найти среднюю и максимальную мощность двигателя автомобиля при разгоне.
Пример 8.Автомобиль массой m = 2000 кг движется вверх по наклонной плоскости под углом α = 150 , развивая на пути S = 100 м скорость vк = 36 км/ч. Коэффициент трения μ = 0,05. Найти среднюю и максимальную мощность двигателя автомобиля при разгоне.
Условие:
m =2000 кг;
S=100 м;
α= 150;
μ=0,05;
v0 =0;
vк =36км/ч = 10м/с;
Рср - ? Рmax - ?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3).
На автомобиль действует четыре силы: сила тяжести FТ=mg, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
 .
.
Это уравнение в проекциях на оси координат
на ось х: ma = F – mg sina - FTP,
на ось у : 0 = N – mg cosa,
FTP = μ N= μ mg cosa,
Выразим из этих уравнений силу тяги F
F = mg sina + μmg cosa + ma.
Ускорение на этом участке равно:
a = (vk2 - v02)/(2s) = vk2/(2s).
Найдем силу тяги двигателя на этом участке:
F = mg sinα + μmgcosα +  = m(gsinα + μgcosα +
= m(gsinα + μgcosα +  )
)
Работа двигателя на этом участке: A = Fscosφ,
Где φ– угол между F и s, равный нулю. Следовательно A = Fs
Подставив сюда выражение для F, получим
А = m(gsinα + μgcosα +  )s
)s
Средняя мощность равна <P> = 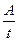 , где
, где 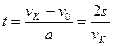 , откуда
, откуда

Максимальная мощность автомобиля достигается в тот момент, когда скорость максимальна: Pmax = F·vk,
Проверка размерности: 
Вычисление:
<P> = 3,58·104 Вт, Pmax = 7·104 Вт.
Ответ: <P> = 3,58·104 Вт, Pmax = 7·104 Вт.
Пример 9.На скамье Жуковского сидит человек и держит в вытянутых руках гири массой m =10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l1 = 50 см. Скамья вращается с частотой n1 = 1,0 с-1. Как изменится частота вращения скамьи и какую работу A произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2 = 20 см. Суммарный момент инерции человека и скамьи относительно оси вращения J =2,5 кг·м2. Ось вращения проходит через центр масс человека и скамьи.
Условие:
m = 10 кг;
l1=50 см = 0,5 м;
n1 =1,0 с-1;
l2 =20 см =0,2 м;
J = 2,5 кг·м2.
n2 - ? А - ?
Решение. Частота вращения скамьи Жуковского изменится в результате действий, производимых человеком при сближении гирь. В системе тел скамья – человек – гири все силы, кроме сил реакции опоры, являются внутренними и не изменяют момента импульса системы. Однако моменты сил реакции опоры относительно вертикальной оси равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими.) Следовательно, момент импульса этой системы остается постоянным:
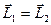 ;
; 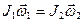 , (1)
, (1)
где J1ω1, J2ω2 - моменты импульса системы соответственно до и после сближения гирь.
Перепишем векторное уравнение (1) в скалярном виде:
J1ω1 = J2ω2. (2)
До сближения гирь момент инерции всей системы: J1 = J0 + 2ml12.
После сближения: J2 = J0 + 2ml22,
где m - масса каждой гири.
Выражая угловую скорость через частоту вращения по формуле
ω = 2πn и подставляя ее в уравнение (1) получаем
(J0 + 2ml12)n1 = (J0 + 2ml22)n2.
Откуда
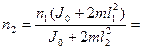 2,3 c-1.
2,3 c-1.
Все внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому изменение кинетической энергии системы равно работе, совершенной человеком:
A = W2 - W1 = 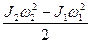 .
.
Учитывая, что ω2 = J1ω1/J2, получаем работу, совершаемую человеком:
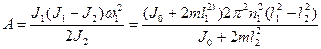
Проверка размерности:
 ,
, 
Вычисление: А = 190 Дж , n2= 2,3 c-1
Ответ: А = 190 Дж , n2= 2,3 c-1
infopedia.su
10.4. Мощность
Скалярная величина
,
характеризующая быстроту совершения работы, называется средней мощностью силы. В СИ мощность выражается в ваттах:
Если в течение некоторого времени t мощность машины остается постоянная или существенно неизменно, то произведена работа выражается формулой:
отсюда и появляется единица времени
10.5. Механический коэффициент полезного действия
В технике работа сил обычно связана с преодолением различных сопротивлений, для выполнения этой работы создается множество разнообразных машин и механизмов.
Силы сопротивления , которые преодолевает любая машина (механизм):
Тогда вся работа совершает машина или механизм:
где – работа по преодолении полезного сопротивления, отсюда:
Отношения полезной работы ко всей совершенной работе называется механический коэффициент полезного действия.
В технике распространены случаи работы машин при их последовательном соединении друг с другом.
Допустим, имеем совокупность трех механизмов с КПД.Если работа совершенная механизмам и их полезная работа , то КПД всех точек механизмов:
Вывод: чем длиннее «цепочка» совместно работающих механизмов, тем меньше её общий КПД, причем общий КПД всегда меньше самого низкого из числа перемножаемых КПД.
10.6. Работа сил на наклонной плоскости
Пусть требуется поднять на высоту h груз, сила тяжести которого G.
Предположим, что подъем осуществляется тремя способами:
Вертикальный
По наклонной плоскости с углом подъема α.
По менее крутой плоскости с углом подъема β (β<α).
Если считать, что груз перемещается равномерно, то работа по подъеме груза во всех 3-х случаях совершаются одинакова:
Но, в первом случае приходится преодолевать силу тяжести G, во втором – , в третьем –
Так как β<α, то , значит
Наклонная плоскость, как одно из средств получения выигрыша в силе при перемещении тяжести, широко использование в технике.
Сила F направлена параллельно наклонной плоскости.
При перемещении вверх по наклонной плоскости тела и на него кроме силы F, действует еще три силы:
– сила тяжести G, нормальная реакция наклонной плоскости Rn,, значение которого равно:
– сила трения Rf , значения которого равно:
При равномерном подъеме тела М четыре силы образуют уравновешенную систему. Алгебраическая сумма работ этих сил равна нулю.
где – работа силы тяжести
–работа силы трения
–работа нормальной реакции
Если же требуется определить значение силы F, то с учетом того, что получаем:
Полезную часть работы сил F составляют работа по подъему тела на высоту и тогда:
Таким образом КПД наклонной плоскости при подъеме груза силой направленной параллельно наклонной плоскости:
Вывод: КПД наклонной плоскости зависит только от ее угла наклона и коэффициента трения при перемещении груза по плоскости.
10.7. Работа и мощность при вращательном движении тел
Допустим, что к рукоятке C колеса, насаженного на ось OZ,
приложена сила , постоянно направленная перпендикулярно . При вращении колеса точка приложения силы перемещается по окружности и элементарная работа этой силы
.
Но так как , то , где произведение называется вращающим моментом. Следовательно, при вращении тела элементарная работа
.
При повороте колеса на угол работа
.
Если при этом вращающий момент , то
(работа при вращении тела равна произведению вращающего момента на угол поворота).
Разделив обе части этого равенства на время действия вращающего момента, получим его мощность:
,
или, так как ,
(мощность при вращении тела равна произведению вращающего момента на угловую скорость).
Из последней формулы вытекает важное следствие:
(при постоянной мощности вращающий момент обратно пропорционален угловой скорости).
studfiles.net
Работа в механике. Мощность. КПД.
Энергию можно изменить (увеличить или уменьшить) путем совершения работы. Работой называют скалярную физическую величину, характеризующую процесс обмена энергией между взаимодействующими телами. Физический смысл имеет лишь работа, совершаемая под действием конкретной силы. Если эта сила постоянна, то работа численно равна скалярному произведению силы на перемещение, совершенное под действием этой силы: , где α – угол между направлением силы и направлением перемещения. Единица измерения работы Джоуль (Дж).
Сила, работа которой не зависит от формы траектории, а зависит только от начального и конечного положения тела, называется потенциальной (консервативной). Работа такой силы по замкнутому контуру (пути) равна нулю. Сила тяжести и сила упругости являются потенциальными, а сила трения и сила сопротивления таковыми не являются.
Связь работы с изменением энергии выражается двумя соотношениями:
1) Работа консервативной силы равна разности потенциальных энергий тела или изменению потенциальной энергии, взятой со знаком минус.
.
2) Изменение кинетической энергии тела равно алгебраической сумме работ всех сил, действующих на тело (теорема об изменении кинетической энергии)
.
Мощность – это скалярная физическая величина, характеризующая быстроту выполнения работы и численно равная отношению работы к промежутку времени, за который она была совершена:
.
Единица измерения в Си Ватт (Вт). Если на тело действует постоянная сила в направлении перемещения, то мощность можно рассчитать по формуле:
,
где v - скорость установившегося движения.
Коэффициент полезного действия – скалярная физическая величина, характеризующая процесс преобразования энергии, который неизменно сопровождается потерями части энергии на преодоление сил трения, рассеяния тепла и т. п. Коэффициент полезного действия (КПД) численно равен отношению полезной работы (энергии, мощности) ко всей затраченной работе (энергии, мощности), выраженному в процентах или долях единицы
.
Дата добавления: 2015-07-07; просмотров: 445 | Нарушение авторских прав
Читайте в этой же книге: ПАМЯТКА СТУДЕНТУ | Предмет изучения и метод научного познания в физике | Основные физические термины | Структура физической теории | Физика и гуманитарные науки. | Основная задача, структура и модели. | Система понятий и законов кинематики | Система понятий и законов динамики | Система понятий и законов статики | Предмет изучения и основное понятие |mybiblioteka.su - 2015-2018 год. (0.006 сек.)mybiblioteka.su
Мощностью силы. Коэффициент полезного действия
Мощность
Мощностью силы называется работа совершаемая в ед.времени. Т.е мощность характеризует быстроту совершения работы.
Средняя мощность равна:
 где N – мощность, А – работа
где N – мощность, А – работа
N = 
1КВТ=103Вт
1л с 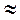 736Вт = 0,736 кВт
736Вт = 0,736 кВт
1КВТ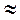 1,36 лс
1,36 лс
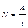 =
=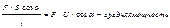
Мощность в данный момент времени:
N=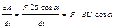
КПД
В процессе выполнения работы движущей силы машин и механ преобладают силы сопротивления которые делятся на:
А) силы полезного сопротивления
Б) силы временного сопротивления
А) силы для преодоления которых построчна машина
Б) Которые машине и механизму приходится вынужденно преодолевать вместе с полезными сопротивлениями явл.силы трения и силы сопротивления окруж.среды
Работа для преодоления полезных сопротивлений назыв.полезной работы движ.сил называется затраченной или просто вся совершенная работа.
Отношение полезной работы ко всей

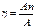 или
или 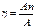

Затраченная работа
An= A – Aв – где Ав работа по преодолению вредных сопротивлений.
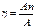 =
=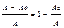 из этой формулы следует что КПД всегда меньше 1 и чем меньше вредное сопротивление тем больше КПД
из этой формулы следует что КПД всегда меньше 1 и чем меньше вредное сопротивление тем больше КПД
Разделим числитель и знаменатель на время t
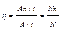
Если ряд мех.соед.последовательно т.е каждый последующий мех.получает движ.от ведомого звена предыдущего механизма, то тогда общий КПД равен произведению КПД всех мех.
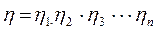
Сопротивление материалов.
сходные понятия и задачи сопромата
Сопромат – наука о прочности, жесткости и устойчивости мех.конструкций и методы их расчета.
Деформацией – назыв.изменения формы и размеров тела под действием приложенных к нему нагрузок.
Упругость – св-во тв.тел принимать первоначальную форму и размеры после прекращения действия силы.
Остаточной или пластической деформацией назыв.Деформацию которая после снятия нагрузки полностью не исчезает т.е тело полностью не возвращается к первоначальным размерам, а получает частичные _
I – ая задача.
Расчет по прочности.
Позволяет определить размеры и форму деталей выдерживающих заданную нагрузку, но не только при заданном значении при некоторых увел. нагруз. т.е конструкция должна иметь запас прочности.
Жесткостью - способность мат.констр. сопротивляться упругим деформациям.
II-ая задача.
Расчет на жесткость.
Расчет в основу которого положено требования ограничения наибольших упругих перемещений ( прогибов)
Устойчивость – способность констр.сопротивляться усилиям стремящимся вывести ее из исходного состояния упругого равновесия.
III – ая задача.
Расчет на устойчивость.
Пример:
Длинный тонкий стержень сжат центрально расположенной силы при вел. силы больше критической, стержень внезапно прогибается в результате первоноч.прямолинейная форма равновесия становится не устойчивой и возникает новая устойчивая форма равновесия _
По этому расчету на устойчивость должен обеспечить такое соотношения нагрузок размеров и св-в мат. при котором гарантированно с определенным запасом устойчивость прямолинейной формы равновесия.
При расчетах на прочн.и жесткость некоторые полож и. теор.мех не применимы.
I Действующие внешние силы нельзя заменить, равнодействующ. или экв. сист.сил. т.к при этом меняется хар-р деформации.
II. Силу нельзя переносить вдоль линии ее действия т.к меняется хар-р деформации.
III. Пару сил нельзя перемещать в плоскости действия пары.
vunivere.ru


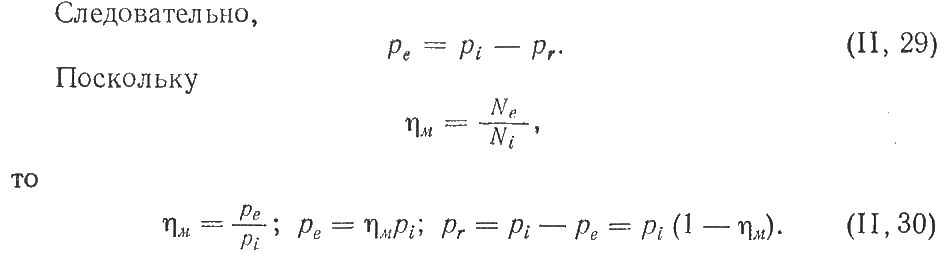








Поделиться с друзьями: