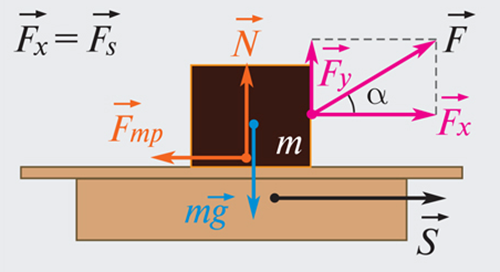
9. Механическая работа и мощность. Что такое работа и мощность

9. Механическая работа и мощность

Если действующая на тело сила вызывает его перемещение, то действие силы характеризуется механической работой

, где - угол между направлением силы и перемещения. Формула справедлива для случая когда тело движется прямолинейно и действующая на него сила остается постоянной. Если сила изменяется, то.

Механическая работа является мерой изменения энергии. За единицу работы в системе Си принимают джоуль (Дж).

Средней мощностью называют величину, равную отношению работык промежутку времени, за который она совершается

Мгновенная мощность определяется по формуле . Учитывая, что, получаем, гдеv – мгновенная скорость.

За единицу мощности в системе СИ принимают ватт (Вт).

На практике часто применяют внесистемную единицу мощности – лошадиную силу.

1 л.с. = 735 Вт

10. Кинетическая и потенциальная энергия

Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией.

Энергия может быть обусловлена движением тела с некоторой скоростью (кинетическая энергия), а также нахождением тела в потенциальном поле сил (потенциальная энергия).

Кинетическая энергия

Рассмотрим случай, когда тело массой m под действием силы F изменяет свою скорость от до. Определим работу силы, приложенной к телу

Так как механическая работа является мерой изменения энергии, то величина представляет собой энергию, обусловленную движениемтела.

Энергию, которой обладает тело вследствие своего движения называют кинетической .

Работа совершаемая силой при изменении скорости тела, равна изменению кинетической энергии тела

Потенциальная энергия тела в поле силы тяжести

При падении тела массой m с высоты до высотынад Землей сила тяжести совершает работу

или .

Сила тяжести является консервативной силой, а поле тяготения – потенциальным. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком

Потенциальная энергия тела в поле силы тяжести .

Энергия, которая определяется взаимным расположением тел или частей одного и того же тела называется потенциальной.

11. Закон сохранения полной механической энергии

Рассмотрим движение тела в замкнутой системе, в которой действуют только консервативные силы. Пусть, например, тело массой m свободно падает. При переходе тела из состояния 1 в состояние 2 сила тяжести совершает работу

В то же время . Следовательно,. Преобразовав данное выражение, получим.

Сумма кинетической и потенциальной энергии тела называется полной механической энергией тела.

Согласно закону сохранения полной механической энергии: полная механическая энергия замкнутой системы тел, взаимодействующих друг с другом только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии в кинетическую и обратно.

Системы, в которых сохраняется полная механическая энергия, называются консервативными.

Системы, в которых полная механическая энергия не сохраняется называются диссипативными (диссипация – переход энергии в другой вид, например, механической во внутреннюю).

В общем случае закон сохранения энергии в природе формулируется следующим образом:

Энергия тел никогда не исчезает и не появляется вновь: она лишь превращается из одного вида в другой или переходит от одного тела к другому.

studfiles.net

Механическая работа: определение и формула

Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?

Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа – это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом. Как так? Сейчас разберемся.

Механическая работа в физике

Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример – это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть. В каком случае совершается механическая работа?

Определение механической работы

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

A=Fs,

где A – работа,F – сила,s – пройденный путь.

Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.

Единица работы – 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример – это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения, то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.

Нужна помощь в учебе?

Предыдущая тема: Воздухоплавание в физике Следующая тема:&nbsp&nbsp&nbspМощность: формула и применение в физике

Все неприличные комментарии будут удаляться.

www.nado5.ru

Работа и мощность силы

Количество просмотров публикации Работа и мощность силы - 1221

Работа и мощность силы. Теорема об изменении кинетической энергии

РАБОТА, МОЩНОСТЬ, ЭНЕРГИЯ

. Единой мерой различных форм движения служит физическая величина, называемая энергией. Для характеристики качественно различных форм движения, изучаемых в физике, вводятся соответствующие им виды (формы) энергии, к примеру, механическая, внутренняя, электромагнитная.

Для количественной характеристики процесса взаимодействия тела с другими телами в механике вводят понятие работы, совершаемой силой.

Пусть материальная точка под действием силы совершает перемещение по некоторой траектории 1-2(рис. 3.1). В общем случае сила в процессе движения точки может меняться как по модулю, так и по направлению. Рассмотрим элементарное перемещение , в пределах которого силу можно считать постоянной.

Действие силы на перемещении характеризуют величиной, равной скалярному произведению , которую называют элементарной работой δA силы на перемещении .

. (3.1)

Рис.3.1

Элементарную работу также можно представить в виде:

, (3.2)

где α - между векторами и , ds =|| - элементарный путь, Fs - проекция вектора на вектор (рис. 3.1).

Величина δA - скалярная. Учитывая зависимость отугла α(или от знака проекции Fsвектора на вектор ) δAдолжна быть положительной, отрицательной и равной нулю (если перпендикулярен , т. е. Fs = 0).

Суммируя (интегрируя) выражение (3.2) по всем элементарным участкам пути от точки 1 до точки 2, найдем работу силы нa данном пути:

. (3.3)

где интегрирование выполняется вдоль траектории.

За единицу работы в системе СИ принимается 1 Дж = 1 Н·м.

Для характеристики скорости, с которой совершается работа͵ вводят величину, называемую мощностью. Мощность - это работа͵ совершаемая силой за единицу времени. В случае если за промежуток времени dt сила совершает работу , то мощность N, развиваемая этой силой в данный момент времени, равна (dt выбирается настолько малым, что силуна данном промежутке можно считать постоянной):

(3.4)

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, мощность, развиваемая силой , равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы.Как и работа͵ мощность является скалярной величиной. Зная мощность силы, можно найти и работу, которую совершает эта сила за промежуток времени t. Представив выражение (3.1) в виде, получим:

. (3.5)

Единицей мощности в СИ является ватт (Вт), равный джоулю в секунду (Дж/с).

referatwork.ru

Механическая работа и мощность

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Если действующая на тело сила вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).

Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.

Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения (рис. 1.18.1):

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Рисунок 1.18.1.

Работа силы :

Если проекция силы на направление перемещения не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:

Это сумма в пределе (Δsi → 0) переходит в интеграл.

Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.18.2).

Рисунок 1.18.2.

Графическое определение работы. ΔAi = FsiΔsi

Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины (рис. 1.18.3).

Рисунок 1.18.3.

Растянутая пружина. Направление внешней силы совпадает с направлением перемещения :

k – жесткость пружины.

Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).

Рисунок 1.18.4.

Зависимость модуля внешней силы от координаты при растяжении пружины

По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:

Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

Модель. Механическая работа.

Мощность

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

questions-physics.ru

Т. Работа и мощность тока — PhysBook

Работа и мощность тока

Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту.

Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи.

Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,

\(~A = qU ,\)

где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.

Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим

\(~A = IUt .\)

Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:

\(~A = I^2Rt = \frac{U^2}{R} t .\)

Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле

\(~A = I(\varphi_1 - \varphi_2 \pm \varepsilon) t .\)

По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.

Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа Ameh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия. В этом случае коэффициент полезного действия можно рассчитать как

\(~A_0 = A_{meh} + Q ;\) \(~\eta = \frac{A_{meh}}{A_0} = \frac{A_{meh}}{A_{meh} + Q} .\)

Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:

\(~A_p = IUt = I^2Rt .\)

Затраченная же работа источника тока равна работе сторонних сил:

\(~A_z = q \varepsilon = I \varepsilon t ,\)

где \(~\varepsilon = I (R + r)\).

Тогда \(~A_z = I^2 (R + r) t\) .

КПД источника \(~\eta = \frac{A_p}{A_z} = \frac{IUt}{I \varepsilon t} = \frac{U}{\varepsilon} = \frac{R}{R + r}\), где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f(R) при r = const приведена на рис. 1.

Рис. 1

Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж.

1 Дж = Кл·В = А·В·с.

Измеряют работу электрического тока счетчиками.

Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле \(~P = \frac At\) или P = IU.

Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока\[~P = I^2R = \frac{U^2}{R}\]. В этом случае речь идет о тепловой мощности.

Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.

Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·106 Дж = 3,6 МДж; 1 гВт·ч = 3,6·105 Дж = 360 кДж.

Для измерения мощности тока существуют специальные приборы — ваттметры.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 267-270.

www.physbook.ru

Механическая работа - это... Что такое Механическая работа?

Механическая работа

Работа силы

Ключевые статьи

См. также: Портал:Физика

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы[1].

Определение

В механике можно ввести понятие работы, исходя из довольно простых представлений[2]

Работа силы (сил) над одной точкой

Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:

Здесь точкой обозначено скалярное произведение[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:

где и — радиус-векторы начального и конечного положения тела соответственно.

Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:

где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что

Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Работа в термодинамике

В термодинамике работа, совершенная газом при расширении[8], рассчитывается как интеграл давления по объёму:

Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

следовательно,

(1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим

Единицей измерения работы в СИ является Джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м 1 эрг = 1 г·см²/с² = 1 дин·см 1 эрг = 10−7Дж

Ссылки

↑ Концепции современного естествознания
↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
1. работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
2. работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
3. работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
4. работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
5. работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).
↑ Механическая работа. Мощность
↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература

Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.

См. также

dik.academic.ru

Каталог товаров