В электротехнике при анализе режимов работы электрических цепей широко используется понятие двухполюсника. Двухполюсникомпринято называть часть электрической цепи произвольной конфигурации, рассматриваемую относительно двух выделенных выводов (полюсов). Двухполюсники, не содержащие источников энергии, называются пассивными. Всякий пассивный двухполюсник характеризуется одной величиной – входным сопротивлением, т.е. сопротивлением, измеряемым (или вычисляемым) относительно двух выводов двухполюсника. Входное сопротивление и входная проводимость являются взаимно обратными величинами. Пусть пассивный двухполюсник содержит одну или несколько индуктивностей и один или несколько конденсаторов. Под резонансным режимом работы такого двухполюсника понимают режим (режимы) двухполюсника при котором входное сопротивление является чисто активным. По отношению к внешней цепи двухполюсник ведет себя как активное сопротивление, вследствие чего входные напряжение и ток совпадают по фазе. Различают две разновидности резонансных режимов: резонанс напряжения и резонанс тока. В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости конденсаторов Спроисходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах, а также активная, реактивная и полная мощности электрической цепи. Зависимости токаI, коэффициента мощности cosи полного сопротивленияZцепи переменного тока в функции емкостного сопротивления (резонансные кривые) для рассматриваемой цепи приведены на рис. 9,а. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 9,б. Как видно из этой диаграммы, реактивная составляющая напряжения ULна катушке при резонансе равна напряжениюUСна конденсаторе. При этом напряжение на катушке индуктивностиUкпри резонансе вследствие того, что катушка кроме реактивного сопротивленияXLобладает еще и активным сопротивлениемR, несколько больше, чем напряжение на конденсаторе. Анализ представленных выражений (2), а также рис. 9,аибпоказывают, что резонанс напряжений имеет ряд отличительных особенностей. 1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т.е. 2. Из этого следует, что при неизменном напряжении питающей сети (U= const) при резонансе напряжений ток в цепи достигает наибольшего значенияI =U/Z =U/R. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки. а)б) Рис. 9 3. Коэффициент мощности при резонансе cos=R/Z =R/R = 1, т.е. принимает наибольшее значение, которому соответствует угол= 0. Это означает, что вектор токаи вектор напряжения сетипри этом совпадают по направлению, так как они имеют равные начальные фазыi=u. 4. Активная мощность при резонансе P=RI 2имеет наибольшее значение, равное полной мощностиS, в то же время реактивная мощность цепиQ=XI 2= (XLXC)I 2оказывается равной нулю:Q =QLQC= 0. 5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными UС=UL=XCI =XLIи в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т.е.UR=U. Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений широко используется в различного рода приборах и устройствах электроники. studfiles.net Активная мощность – это энергия, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R . [Вт]. (2.49) Реактивная мощность – это энергия, которой обмениваются генератор и приемник. Под реактивной мощностью Q понимают: .[Вар] (2.50) Если и наоборот – Полная мощность [ВА]. (2.51) Графически связь между мощностями представляют в виде треугольника мощности, у которого два катета Р и Q и гипотенуза S. Рисунок 2.12 – Треугольник мощностей Косинус угла сдвига фаз называетсякоэффициентом мощности. Он показывает, какую долю полной мощности составляет активная мощность, а какая доля электроэнергии преобразуется в другие виды энергии. Когда , то это означает, что активная мощность равна полной или сопротивление потребителя только активное. Коэффициент мощностиважный эксплуатационный параметр электроприемников. Так как , (2.52) то чем выше , тем при меньшем значении тока в цепи происходит преобразование электроэнергии в другие виды энергии, что приводит к уменьшению потерь электроэнергии, ее экономии и снижению стоимости устройств электропередачи. Повышение коэффициента мощности Во многих электротехнических устройствах преобладает индуктивная составляющая реактивного тока, т.е. большой положительный угол сдвига фаз φ между напряжением и током, что ухудшает коэффициент мощности. Низкое значение приводит к неполному использованию технических и электротехнологических систем, которые загружаются реактивной (индуктивной) составляющая тока, что приводит к увеличению потерь энергии. Для увеличения параллельно электротехническому устройству включают батарею конденсаторов. Емкостный (реактивный) ток компенсирует индуктивный ток. Баланс мощности в цепи синусоидального тока Баланс мощности заключается в том, что: 1. Алгебраическая сумма активных мощностей всех источников энергии равная арифметической сумме мощностей всех резистивных элементов (2.53) 2. Алгебраическая сумма реактивных мощностей источников энергии равна разности между арифметическими суммами реактивных мощностей индуктивных элементов и емкостных элементов (2.54) Баланс мощностей можно выразить и в комплексной форме: алгебраическая сумма комплексных мощностей источников энергии равна алгебраической сумме комплексных мощностей потребителей энергии (2.55) Знаки алгебраических слагаемых источников энергии выбираются по правилу для активных мощностей: знак «+» если направления действия ЭДС совпадает с направлением действия тока и «–», если не совпадают. В качестве критерия режима «резонанс» в электрических цепях, содержащих катушки индуктивности и конденсаторы, принимается совпадение по фазе тока и напряжения на входных зажимах, т. е. фазовый резонанс. Если конденсатор зарядить до какого-то напряжения, то его разряд на катушку и повторный заряд имеет колебательный характер. При свободных колебаниях в отсутствии потерь напряжение на обкладках конденсатора меняется во времени по косинусоидальному, а ток в катушке – по синусоидальному законам. В реальном колебательном контуре кроме катушки индуктивности и емкостного элемента должен быть и резистивный элемент. При подключении колебательного контура к источнику энергии могут возникать резонансные явления. Различают два основных вида резонанса: резонанс напряжений при последовательном соединении контура с источником энергии и резонанс токов – при параллельном соединении. Резонанс напряжений Рисунок 2.13 – Последовательный колебательный контур По закону Ома комплекс тока в контуре будет (2.56) где Z – комплексное сопротивление контура, определяемой формулой (2.38). Полное сопротивление контура и угол сдвига фаз из формул (2.41) и (2.42). Тогда действующее значение тока равно: (2.57) Резонанс возникает при равенстве индуктивных и емкостных сопротивлений: . (2.58) При этом начальные фазы тока и напряжения будут равны ,. Полное сопротивление минимально и равно, а действующее значение тока придостигнет максимального значения: (2.59) Резонанс напряжений – это режим неразветвленной цепи, при котором ток и напряжение совпадают по фазе, а действующие значения напряжений на индуктивном и емкостном элементах равны, но противоположны по фазе. Рисунок 2.14 – Векторные диаграммы режимов резонанса напряжений (а) и резонанса токов (б) Из условия (2.58) следует, что резонанса можно достичь, изменяя частоту напряжения питания или параметры цепи: индуктивность или емкость. Резонансная угловая частота – частота, при которой наступает резонанс: . (2.60) Отношение напряжения на индуктивном элементе или емкостном элементек напряжению питания при резонансеназывают добротностью контура или коэффициентом резонанса: (2.61) Частотные характеристики и резонансные кривые последовательного контура. Изменение частоты ω приводит к изменению параметров контура, т. е. изменяется его реактивное сопротивление, а также угол . Зависимость от частоты параметров цепи (XL и XC) называется частотными характеристиками цепи, а зависимость действующих (или амплитудных) значений тока и напряжения от частоты – резонансными кривыми. Рисунок 2.15 – Частотные характеристики последовательного контура Изменение реактивного сопротивления приводит к изменению режима цепи. На рисунке 2.16 показан примерный вид резонансных кривых: тока , напряжений на емкостноми индуктивномэлементах, а также угла φ для цепи с добротностьюQ ≈1,25. Рисунок 2.16 – Резонансные кривые последовательного контура Резонансные кривые рисунка 2.17 показывают, что чем выше добротность Q, тем острее резонансная кривая и лучше избирательные свойства цепи, для оценки которых пользуются понятием полосы пропускания, что является разницей верхней и нижней частот . Пересечениес резонансными кривыми и определяет граничные частоты. Рисунок 2.17 –Резонансные кривые для цепей с различной добротностью Резонанс токов может возникнуть в цепи, схема которой содержит параллельно соединенные индуктивный, емкостной и резистивный элементы. Резонанс наступает, когда у входной проводимости (2.62) равны противоположные по фазе реактивные составляющие токов . Поэтому такой резонанс и называется резонансом токов. Рисунок 2.18 – Параллельный колебательный контур При резонансе полная проводимость контура минимальна , и общий ток также минимален (2.64) Резонанс токов – это режим участка цепи с параллельными ветвями, при котором сдвиг фаз между напряжением на его выводах и общим током равен нулю. На рисунке 2.19 б приведены резонансные кривые параллельного контура. Точка пересечения кривых исоответствует резонансу токов, при котором. Рисунок 2.19 – Частотные характеристики (а) и резонансные кривые (б) параллельного контура Резонанс напряжений – явление нежелательное, т. к. приводит к перенапряжениям в цепях, которые могут в несколько раз превышать рабочее напряжение установки. Резонанс токов – явление безопасное для установок. Явление резонанса применяется в радиотехнике при настройке контуров на резонансную частоту. studfiles.net Технико-экономическое значение коэффициента мощности cosφ заключается в том, что от его значения зависят эффективность использования электрических установок и, следовательно, капитальные и эксплуатационные расходы. Активная мощность, развиваемая генератором при номинальном режиме где UНОМ – номинальное напряжение генератора; IНОМ – номинальный ток, который при длительном прохождении вызывает предельно допустимое нагревание генератора. Полное использование мощности генератора происходит, когда cosφ=1. В этом случае активная мощность Р максимальна и равна номинальной полной мощности Влияние значений cosφ на режим работы оборудования: 1) уменьшение cosφ, значение которого определяется характером нагрузки, приводит к неполному использованию генератора; 2) уменьшение cosφ при постоянной мощности потребителя Р приводит к увеличению тепловых потерь в линии передачи, которые растут обратно пропорционально квадрату коэффициента мощности . (16) где Р0 – потери в линии при cosφ=1. Для полного использования номинальной мощности генераторов и уменьшения тепловых потерь необходимо повышать cosφ приемников энергии до значений, близких к единице (0,95–1,0). В этом случае потребитель меньше нагружает линию реактивной мощностью. Способы повышения коэффициента мощности: 1) естественный – правильный выбор оборудования и его эксплуатация; 2) подключение параллельно приемнику батарей конденсаторов в случае индуктивной нагрузки (асинхронные двигатели). Благодаря этому источником реактивной энергии для приемника становится емкость и линия передачи разгружается от реактивного тока. Разберем следующие вопросы: Коэффициент мощности электрической цепи синусоидального тока называется … отношение активной мощности Р к полной мощности S отношение полной мощности S к активной мощности Р произведение активной мощности Р на полную мощность S активная мощность Р Активную мощность Р цепи синусоидального тока можно определить по формуле… Если Q и S – реактивная и полная мощности пассивной электрической цепи синусоидального тока, то отношение Q к S равно… tg φ arcsin φ Вывод по четвертому вопросу: синусоидальные токи и напряжения как функции времени могут быть описаны различными способами: алгебраически, векторными диаграммами и комплексами. 1) Процессы, протекающие в однофазных цепях переменного тока со смешанным последовательным соединением приемников, характеризуются появлением понятий полного сопротивления, полной мощности, треугольников сопротивлений и мощностей, повторяющих треугольник напряжений. В них также необходимо учитывать взаимные фазовые сдвиги напряжений и токов. Умение анализировать однофазные цепи со смешанным соединением резисторов является важным при изучении трехфазных цепей, принципа действия и устройства электрических машин. 2) Для расчета параллельного соединения приемников используется метод проводимостей. 3) При резонансном режиме работы цепи, содержащей приемники различного характера, ее сопротивление является чисто активным. Различают резонансы токов и напряжений, которые используются в радиотехнике и повышения коэффициента мощности. 3) От значения коэффициента мощности зависят эффективность использования электрических установок и, следовательно, капитальные и эксплуатационные расходы. Для его повышения необходимо правильно выбирать оборудование и условия его эксплуатации. studfiles.net Итак, только активная составляющая тока определяет преобразование электроэнергии в другие виды энергии, т. е. позволяет количественно оценить совершаемую работу. Реактивная же составляющая тока никакой работы не производит. Однако при ее наличии увеличивается полный ток. Рис. 8.5. Электрическая цепь с параллельным включением конденсатора для повышения коэффициента мощности:а ¾ схема; б ¾ векторная диаграмма токов Представим электроприемник, потребляющий активную и индуктивную составляющие тока, схемой последовательного соединения элементов Rпр и Lпр (рис. 8.5, а). На векторной диаграмме (рис. 8.5, б) вектор тока приемника В отсутствие емкости С, включенной параллельно с приемником Так как в данном случае Iл = Iпр = Pпр / (Uсos jпр), то при постоянной мощности приемника и постоянном питающем напряжении (Рпр = const и U = const) с уменьшением коэффициента мощности Сos jпр увеличиваются ток, в линии, а следовательно, и потеря мощности Pп.л = (P2пр R/U2) (1/cosjпр). Таким образом, для уменьшения потерь мощности в передающих устройствах необходимо увеличивать коэффициент мощности приемников электроэнергии. Каждому промышленному предприятию задают то средневзвешенное значение коэффициента мощности (реактивной мощности), которое должно быть обеспечено. Получению заданного коэффициента мощности способствует правильный выбор электрооборудования. Однако при этом всегда необходимо принимать дополнительные меры, например, использовать батареи конденсаторов и т. д. Конденсаторы емкостью С включают параллельно электроприемнику (рис. 8.5, а). Ток При емкости конденсатора, равной С, и токе Угол сдвига фаз jмежду напряжением С увеличением емкости конденсатора ток IС = ВСU = w CU увеличивается так, что при некотором значении емкости Срез можно получить равенство IС = IL (режим резонанса токов). В этом случае реактивная составляющая тока приемника IL полностью компенсируется и ток в линии достигает минимального значения, равного активной составляющей тока приемника Iа.пр (рис. 8.5, б). При дальнейшем увеличении емкости конденсаторов IС > IL и реактивная составляющая тока в линии, а, следовательно, и полный ток в ней увеличиваются. Наступает режим перекомпенсации, когда реактивная составляющая тока в линии носит емкостной характер. На рис. 8.6 показано, как изменяется ток Iл при изменении емкости С конденсатора при Рпр = const и U = const. Сначала с ростом С ток Iл уменьшается, достигая минимума в режиме резонанса токов, а затем снова начинает увеличиваться. Коэффициент мощности изменяется в обратном порядке, достигая максимума при полной компенсации (cos Рис. 8.6. Зависимость тока в линии и коэффициента мощности от емкости конденсаторов:I ¾ область недокомпенсации, II ¾ область перекомпенсации Для обеспечения заданного значения коэффициента мощности необходимо устанавливать конденсаторы определенной мощности или емкости. Если электроприемники имеют мощность Р = const и cоsjпр, то они потребляют из сети реактивную индуктивную мощность Qпр = P tgjпр. При заданном значении cоsj2, которое должно обеспечить предприятие (cоsj2 > cоsjпр), потребляемая реактивная мощность Q2 = P tgj2. Разность реактивных мощностей Qпр - Q2 компенсируется емкостной реактивной мощностью конденсаторов Qc = Qпр - Q2 = Р(tgjпр - tgj2). (8.8) Реактивную мощность конденсаторов можно также определить не формуле: Qc = BCU2 = w CU2. (8.9) Приравнивая правые части уравнений (8.8) и (8.9), получим C = P (tgjпр - tgj2) / (2pfU2). При этом емкость выражается в фарадах, если мощность выражена в ваттах, а напряжение ¾ в вольтах. Для полной компенсации (j2 = 0) необходимо, чтобы С = Ptgjпр / (2pfU2). Таким образом, на лекции рассмотрены вопросы, характеризующие мощность в однофазной цепи синусоидального тока, ее вариации, коэффициент мощности и способы его повышения. Рекомендация: Для самоконтроля полученных знаний выполните тренировочные заданияиз набора объектов к текущему параграфу Читайте также: lektsia.comРезонансные режимы работы электрических цепей. Активная мощность равна полной мощности в режиме резонанса если коэффициент мощности
Резонансные режимы работы электрических цепей
Резонанс напряжений
2.6 Активная, реактивная и полная мощности
2.7 Резонанс в цепях синусоидального тока
Вопрос №4. Коэффициент мощности и его технико-экономическое значение (10 мин.)
5. Заключение (10 мин.)
ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ
⇐ ПредыдущаяСтр 8 из 14Следующая ⇒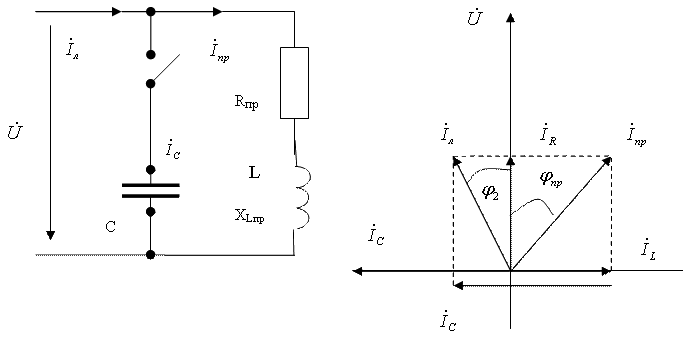
 составляет с вектором напряжения
составляет с вектором напряжения 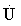 угол jпр, причем
угол jпр, причем
 , ток
, ток  в линии передачи равен току
в линии передачи равен току  приемника. Если в проводах линии передачи (сопротивление которых R) протекает ток
приемника. Если в проводах линии передачи (сопротивление которых R) протекает ток  , то теряемая в них мощность Рп.л =RI2.
, то теряемая в них мощность Рп.л =RI2. конденсатора является практически чисто реактивным, опережающим напряжение на угол p/2 (рис. 8.5, б). Этот ток компенсирует реактивную индуктивную составляющую тока приемника, в результате чего общая реактивная составляющая тока уменьшается.
конденсатора является практически чисто реактивным, опережающим напряжение на угол p/2 (рис. 8.5, б). Этот ток компенсирует реактивную индуктивную составляющую тока приемника, в результате чего общая реактивная составляющая тока уменьшается. ток в линии
ток в линии 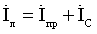 , или Iл <Iпр.
, или Iл <Iпр.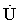 и током
и током  уменьшился, а коэффициент мощности увеличился (cоs j2 >cоs jпр).
уменьшился, а коэффициент мощности увеличился (cоs j2 >cоs jпр). = 1 при IС = IL). Следует помнить, что при подключении конденсаторов потребляемая реактивная индуктивная мощность электроприемника остается неизменной, но ее источником становится батарея конденсаторов, установленная вблизи приемника. В результате в линии передачи реактивные токи уменьшаются.
= 1 при IС = IL). Следует помнить, что при подключении конденсаторов потребляемая реактивная индуктивная мощность электроприемника остается неизменной, но ее источником становится батарея конденсаторов, установленная вблизи приемника. В результате в линии передачи реактивные токи уменьшаются.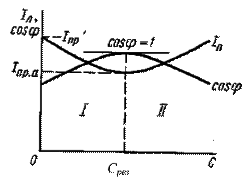
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''











Поделиться с друзьями: