Анализ избирательных цепей в частотной и временной областях Составим систему уравнений согласно первым и вторым законами Кирхгофа для мгновенных значений токов и напряжений (2.1): .(2.1) Из первого уравнения (2.2): .(2.2) Из второго уравнения (2.3): .(2.3) Из третьего уравнения (2.4): .(2.4) Подстановка (2.4) в уравнение (2... Идентификация и моделирование нелинейной системы электромеханического следящего привода с трехпозиционным реле Преобразуем схему следящей системы относительно входного сигнала нелинейного элемента. В автономной системе в режиме стабилизации угла поворота рабочего механизма входное воздействие , тогда Передаточная функция линейной части имеет вид... Исследование искажений сигналов на выходе фильтра нижних частот Получим уравнения состояния цепи с помощью формальной процедуры, для чего заменим L-элементы на источники тока i(t)L1 и i(t)L2 , а C- элемент на источник напряжения u(t)С1... Основные свойства и методы расчета линейных цепей постоянного тока Метод уравнений Кирхгофа позволяет рассчитать режим любой цепи, при любой форме сигнала, в любой момент времени. Пусть требуется найти токи ветвей схемы, у которой число ветвей равно nв и есть nj источников тока, следовательно... Проектирование автоматической системы пожаротушения Согласно п. 4.3 [3] дымовые пожарные извещатели следует устанавливать, как правило, на потолке. При невозможности такой установки допускается размещать их на стенах, балках, колоннах. Необходимо также учесть... Проектирование суммирующего двоично-десятичного счетчика импульсов В картах Карно выделены клетки, которые описываются наиболее простыми логическими уравнениями, и охватывающие все единичные состояния триггеров. Исходя из этого... Расчет и исследование линейной электрической цепи с источниками постоянных воздействий и при заданной угловой частоте питающего напряжения По первому закону Кирхгофа: A: i2(t)-i4(t)-i1(t)=0 B... Расчет линейной электрической цепи при гармоническом воздействии Для расчета токов и напряжений в сложной электрической цепи составим систему уравнений по методу контурных токов. Рис. 7 - Схема сложной цепи Сначала составим граф электрической схемы, согласно которому выберем независимые контуры... Расчет линейной электрической цепи при гармоническом воздействии Для определения токов и напряжений на всех элементах цепи при известных значениях R, C и E необходимо составить систему уравнений по методу контурных токов. Рисунок 4.1 Вначале составляется граф данной электрической цепи... Расчет установившихся режимов в линейных электрических цепях а) Порядок сложности электрической цепи: в испытательной схеме (рисунок 1) 5 ветвей, по ним протекает 5 токов, которые мы должны определить. Количество уравнений, составленных по законам Кирхгофа, равно количеству ветвей в схеме, то есть равно 5... Синтез счетчика импульсов С помощью карт Карно получаем минимизированные логические уравнения для каждого из входов каждого триггера. Для упрощения проектирования счетчика я заменила полученные логические уравнения, по правилу Де - Моргана... Синтез счетчиков импульсов В картах Карно выделены клетки, которые описываются наиболее простыми логическими уравнениями, и охватывающие все единичные состояния триггеров. Исходя из этого... Синхронный счетчик с преобразователем кода на выходе Основываясь на картах входов составляем логические функции входов триггеров A, B... Система автоматического регулирования скорости вращения двигателя 1) Напряжение рассогласования получается за счет разности задающего напряжения и напряжения с тахогенератора: 2) Напряжение Uвг на выходе электронного усилителя пропорционально напряжению рассогласования: гдеК1 - коэффициент усиления... Системы документальной электросвязи Таблица разрешенных комбинаций составляется путем сложения двух, трех, четырех и пяти строк образующей матрицы. Код (10,5) имеет 25 = 32 разрешенных комбинаций. Первая комбинация состоит из пятнадцати нулей (в таблице она не указана)... radio.bobrodobro.ru 2) определить токи во всех ветвях схемы, используя метод контурных токов; 3) определить токи во всех ветвях схемы на основании метода наложения; 4) составить баланс мощностей для заданной схемы; 5) результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить; 6) определить ток во второй ветви методом эквивалентного генератора; 7) построить потенциальную диаграмму для любого замкнутого кон- тура, включающего обе ЭДС. 2) определить токи во всех ветвях схемы, используя метод контурных токов; 3) определить токи во всех ветвях схемы на основании метода наложения; 4) составить баланс мощностей для заданной схемы; 5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить; 6) определить ток во второй ветви методом эквивалентного генератора; 7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Дано: Е1= 40 В, Е2 = 60 В, R1 = 18 Ом, R2 = 36 Ом, R3 = 16 Ом, R4 = 24 Ом, R5 = 40 Ом, R6 = 34 Ом, r01 = 2 Ом, r02 = 4 Ом. Определить: I1, I2, I3, I4, I5. 1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях. Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи. При расчете данным методом произвольно задаем направление токов в ветвях I1, I2, I3, I4, I5. Составляем систему уравнений. В заданной цепи пять ветвей, значит, в системе должно быть пять уравнений (m = 5). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n - 1) независимых уравнений. В нашей цепи три узла (А, В, С), значит, число уравнении n - 1 = 3-1 = 2. Составляем два уравнения для любых 2-х узлов, например, для узлов В и С. узел В: I1 + I2 = I4 узел С: I3 + I5 = I2 Всего в системе должно быть пять уравнений. Два уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие. Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа. Контур АДСВА - обход по часовой стрелке: Е2 - E1 = I2 (R2 + r02) – I1 (R1 + r01) + I3(R3 + R6) Контур ABA'A - обход по часовой стрелке: E1 = I1(R1+r01)+I4R4 Контур А'СВА' — обход против часовой стрелки: E2 = I2(R2 + r02)+I4R4 + I5R5 ЭДС в контуре берется со знаком “+”, если направление ЭДС совпадает с обходом контура, если не совпадает – знак “-”. Падение напряжения на сопротивлении контура берется со знаком “+”, если направление тока в нем совпадает с обходом контура, со знаком “-” если не совпадает. Мы получили систему из пяти уравнений с пятью неизвестными: Решив систему, определим величину и направление тока во всех ветвях схемы. Если при решении системы ток получается со знаком “-” значит его действительное направление обратно тому направлению, которым мы задались. 2) Определить токи во всех ветвях схемы, используя метод контурных токов. Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1. Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной. Итак, в заданной цепи (рис. 1.38) можно рассмотреть три контура-ячейки (АДСВА, ABA'А, А'СВА') и ввести для них контурные токи Ik1, Ik2, Ik3. Контуры-ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления. При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур - ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим: Подставляем в уравнение численные значения ЭДС и сопротивлений. или Сократив первое уравнение на 4, второе – на 4,третие – на 10, получим: Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ1, Δ2, Δ3. Вычисляем контурные токи: Действительные токи ветвей: 3) Определить токи во всех ветвях схемы на основании метода наложения. По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности. а) Определяем частные токи от ЭДС E1, при отсутствии ЭДС Е2, т. е. рассчитываем цепь по рис. 1.39. Показываем направление частных токов от ЭДС Е1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания" Ток источника Применяя формулу разброса и 1-й закон Кирхгофа, вычисляем токи ветвей: б) Определяем частные токи от ЭДС E2 при отсутствии ЭДС Е1,т.е. рассчитываем простую цепь по рис. 1.40. Показываем направление частных токов от ЭДС Е2 и обозначаем их буквой I с двумя штрихами (I"). Рассчитываем общее сопротивление цепи: Вычисляем ток источника: Применяя форму разброса и 1-й закон Кирхгофа, вычисляем токи ветвей: Вычисляем токи ветвей исходной цепи (рис. 1.38), выполняя алгебраическое сложение частных токов, учитывая их направление: 4) Составить баланс мощностей для заданной схемы. Источники E1 и Е2 вырабатывают электрическую энергию, т. к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так: Подставляем числовые значения и вычисляем С учетом погрешности расчетов баланс мощностей получился. 5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить. Метод расчета метод наложения 0,625 0,522 0,232 1,147 0,290 Расчет токов ветвей обоими методами с учетом ошибок вычислений практически одинаков. 6) Определить ток во второй ветви методом эквивалентного генератора. Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2служит источником электрической энергии, т. е. генератором). Получается схема замещения (рис. 1.41) На схеме искомый ток I2 определим по закону Ома для замкнутой цепи: , где Еэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ = Uхх. rэ - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.42), т. е. при отключенном потребителе R2 от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину: Зная Iхх, величины сопротивлений и ЭДС, в схеме можно определить Uхх как разность потенциалов между клеммами а и б. Для этого потенциал точки б будем считать известным и вычислим потенциал точки а. тогда Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис. 1.43), при этом ЭДС Е2 и E1 из схемы исключается, а внутренние сопротивления этих источников r01 и r02 в схеме остаются. Вычисляем эквивалентное сопротивление схемы (рис. 1.43) относительно зажимов а и б. Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви: т. е. ток в этой ветви получился таким же, как и в пунктах 2 и 3. 7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Возьмем контур АДСВА. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю φА=0 (рис. 1.38). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А. 0 - проверочная точка. Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, во оси ординат - потенциалы точек с учетом их знака. zakon.znate.ru Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. При составлении расчетной схемы учитываются ее параметры, указанные в задании, т.е. на схеме показываются только те источники питания, которые предусмотрены таблицей вариантов: источники ЭДС заменяются перемычками, если Е = 0, а источники тока разрывом, если J= 0. При расчете схемы внутренние сопротивления источников ЭДС принять равными нулю, т.е. полагать источники идеальными. Источники тока J и включенные параллельно с ними сопротивления rпар. следует заменить эквивалентными источниками ЭДС E с внутренними сопротивлениями rвн., используя формулы эквивалентного преобразования Рисунок. 2 E = Jrпар. rвн. = rпар. Рисунок. 3 Уравнения контурных токов имеют вид: Где: =7+4+5=16 Ом =4+4+3=11 Ом =5+3+2=10 Ом =4 Ом =5 Ом =3 Ом =18+20=38 В =-20+12=-8 В =0 В Подставляем значения в систему: Составляются определители контурных уравнений: основной и дополнительные = =16×11×10+−4×−3×−5+−5×−4×−3−5×11×−5−−3×−3×16−10×−4×−4=1061 1= =38×11×10+−4×−3×0+−5×−8×−3−0×11×−5−−3×−3×38−10×−8×−4=3398 2= =16×−8×10+38×−3×−5+−5×−4×0−−5×−8×−5−0×−3×16−10×−4×38=1010 3= =16×11×0+−4×−8×−5+38×−4×−3−−5×11×38−−3×−8×16−0×−4×−4=2002 По найденным определителям вычисляются контурные токи: I11 = 1 / =3398/1061 = 3,202 А;I22 = 2 / = 1010/1061 = 0,951 А; I33 = 3 / = 2002/1061 = 1,887 А. По контурным токам определяются токи в ветвях цепи: I1 = -I11 = -3,202А; I2 = I11 - I22 = 3,202 – 0.951 = 2,251 А; I3 = I33- I11 = 1,887-3,202=-1,315А; I4 = I22= 0,951 А; I5 = I22 -I33= 0,951 – 1,887 = - 0,936 А; I6 =- I33 = -1,887 А. Записать систему уравнений Кирхгофа, необходимых для определения токов во всех ветвях схемы и выполнить проверку расчета цепи методом контурных токов На схеме (рис. 3) указываются направления токов I 1, I2, I3, I4 , I5, I6 в ветвях с учетом их знаков и направлений контурных токов и составляются узловые уравнения по первому закону Кирхгофа для независимых узлов 1, 2, и 3. Число независимых уравнений на единицу меньше общего числа узлов в цепи. -I1 – I2 – I4 = 0; I2 + I3 + I5 = 0; I4 + I6 – I5 = 0. Выбираются независимые контуры и произвольно принимаются направления их обхода; для всех контуров по второму закону Кирхгофа составляются контурные уравнения. -I1 R1 + I2 R2 – I3 R3 = E1 + E2; -I2 R2 + I4 R4 + I5 R5 =- E2 +E4; I3 R3 -I5 R5 - I6 R6 = 0. -I1 R1 + I2 R2 – I3 R3 =3,202x7+2,251x4+1,315x5=22,414+9,004+6,575= 37,993 В E1 + E2=18+20=38 В -I2 R2 + I4 R4 + I5 R5= -2,251х4+0,951х4-0,936х3=-9,004+3,804-2,808=-8,008 В - E2 +E4=-20+12=-8 В I3 R3 -I5 R5 - I6 R6=-1,315х5+0,936х3+1,887х2=-6,575+2,808+3,774=0.007 В Выделить в схеме три сопротивления, включенные по схеме треугольника, и заменить их эквивалентным соединением по схеме звезды Рисунок. 4 На рис. 4 указано, что треугольником соединены сопротивления R1; R2; R3. Сопротивления эквивалентного соединения в звезду имеют значения: R12 = R1 R2/ (R1 + R2 + R3) = 28/16=1,75 Ом; R13 = R1 R3/( R1 + R2 + R3 ) = 35/16=2,19 Ом; R23 = R2 R3/(R1 + R2 + R3) =20/16= 1,25 Ом; Рисунок. 5 Рисунок. 5 Для определения напряжения UАВ составляется уравнение по второму закону Кирхгофа для замкнутого контура, который показан штриховой линией на рис. 5 UАВ – I1R1 – I3 R3 + Е2 = 0 Из этого уравнения находится UАВ UАВ = - Е2+ I1 R1 + I3 R3 = -20 +22,414 +6,575 = 8,989 В. megapredmet.ru1.2 Составление системы уравнений для расчёта тока во всех ветвях схемы по законам Кирхгофа. Составить систему уравнений для расчета токов во всех ветвях схемы
1.2 Составление системы уравнений для расчёта тока во всех ветвях схемы по законам Кирхгофа. Расчет и исследование линейной электрической цепи с источниками постоянных воздействий и при заданной угловой частоте питающего напряжения
Похожие главы из других работ:
2. Определение дифференциального уравнения относительно отклика цепи по методу уравнений Кирхгофа
2. Составление дифференциальных уравнений замкнутой нелинейной САУ
5. Составление уравнений состояний цепи
1. Метод уравнений Кирхгофа
2.2 Составление структурной схемы системы обнаружения пожара
1.5 Составление минимизированных логических уравнений
2.2 Система уравнений цепи по законам Кирхгофа для мгновенных значений токов и напряжений
4. Составление системы уравнений для расчета токов и напряжений
4. Составление системы уравнений для расчета токов и напряжений
1.6.1 Метод расчета по законам Кирхгофа
1.4 Составление минимизированных логических уравнений.
Составление минимизированных логических уравнений
1.7 Составление уравнений входов
3.1 Составление исходной системы уравнений
1.2 Составление таблицы всех разрешенных комбинаций
1 составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы
1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;
1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы; № варианта Е1 Е2 R1 R2 R3 R4 R5 R6 r01 r02 3 20 40 64 48 32 25 51 15 1 2 Ток в ветви I1,A I2,A I3,A I4,A I5,A метод контурных токов 0,624 0,522 0,232 1,146 0,290 Пользуясь данными таблицы, составить расчетную схему электрической цепи

 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.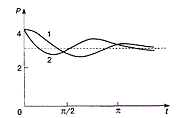 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''

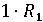









Поделиться с друзьями: