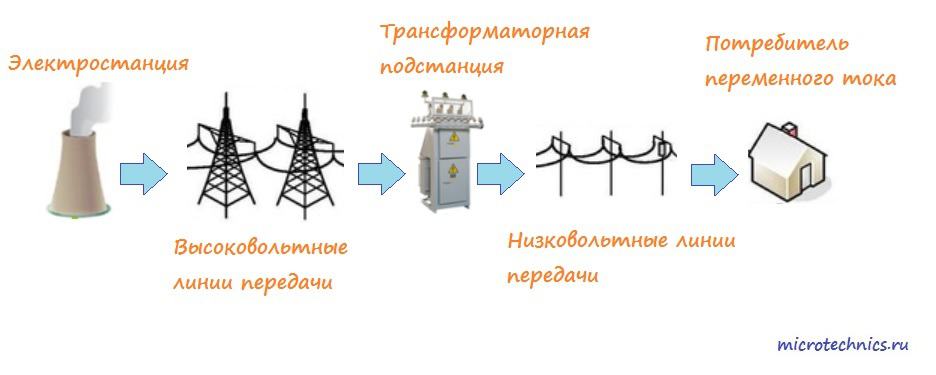
Приветствую всех на нашем сайте в рубрике “Электроника для начинающих”! В предыдущей статье мы обсудили понятия тока, напряжения и сопротивления, но все наши примеры были связаны только с постоянным током, поэтому сегодня мы будем разбираться с переменным 🙂 Итак, переходим от слов к делу! Давайте для начала выясним какова же область применения цепей переменного тока. А область довольно-таки обширна 😉 Смотрите сами – все бытовые электронные приборы, компьютеры, телевизоры и т. д. являются потребителями переменного тока, соответственно, все розетки в нашем доме работают именно с переменным током. Почему же для данных целей не используется постоянный ток? На этот вопрос можно дать сразу несколько ответов. Во-первых, гораздо проще преобразовать напряжение переменного тока одной величины в напряжение другой величины, чем произвести аналогичные “махинации” с постоянным током. Данные преобразования осуществляются при помощи трансформаторов, о которых мы обязательно поговорим в рамках нашего курса. Зачем вообще нужно изменять напряжение переменного тока? С этим тоже все просто и логично. Давайте для примера рассмотрим ситуацию передачи сигнала с электростанции в отдельно взятый дом. Как видите, с электростанции “выходит” высоковольтное переменное напряжение, затем оно преобразуется в низковольтное (к примеру, 220В), а затем уже по низковольтным линиям передачи достигает своей цели – а именно потребителей. Возникает вопрос – к чему такие сложности? Что ж, давайте разберемся… Задачей электростанции является генерировать и передавать сигнал большой(!) мощности (ведь потребителей много). Поскольку величина мощности прямо пропорциональна и значению тока и значению напряжения, то для достижения необходимой мощности нужно, соответственно, либо увеличивать ток, либо напряжение сигнала. Увеличивать значение тока, протекающего по проводам довольно проблематично, ведь чем больше ток, тем больше должна быть площадь поперечного сечения провода. Это связано с тем, что чем меньше сечение проводника, тем больше его сопротивление (вспоминаем формулу из статьи про сопротивление). Чем больше сопротивление, тем больше будет нагреваться провод и, соответственно, рано или поздно он прогорит. Таким образом, использование токов огромной величины нецелесообразно, да и экономически невыгодно (нужны “толстые” провода). Поэтому мы логически приходим к выводу, что абсолютно необходимо передавать сигнал с большим значением напряжения. А поскольку в домах у нас требуются низковольтные цепи переменного тока, то сразу же становится понятно, что преобразование напряжения просто неизбежно =) А из этого и вытекает преимущество переменного тока над постоянным (именно для данных целей), поскольку как мы уже упомянули – преобразовывать напряжение переменного тока на порядок легче, чем постоянного. Ну и еще одно важное преимущество переменного тока – его просто проще получать. И раз уж мы вышли на эту тему, то давайте как раз-таки и рассмотрим пример генератора переменного тока 😉 Итак, генератор – это электротехническое устройство, задачей которого является преобразование механической энергии в энергию переменного тока. Давайте рассмотрим пример: На рисунке мы видим классический пример генератора переменного тока. Давайте разбираться, как же он работает и откуда тут появляется ток 😉 Но для начала пару слов об основных узлах. В состав генератора входит постоянный магнит (индуктор), создающий магнитное поле. Также может использоваться электромагнит. Вращающаяся рамка носит название якоря. В данном случае якорь генератора имеет только одну обмотку/рамку. Именно эта обмотка и является цепью переменного тока, то есть с нее и снимается переменный ток. Переходим к принципу работы генератора переменного тока… Магнит создает поле, вектор индукции которого B изображен на рисунке. Проводящая рамка площадью S равномерно вращается вокруг своей оси с угловой скоростью w. Поскольку рамка вращается, угол между нормалью к плоскости рамки и магнитным полем постоянно меняется. Запишем формулу для его расчета: Здесь Вспоминаем курс физики и записываем выражение для магнитного потока, проходящего через рамку: Величина магнитного потока, как и угол Согласно закону Фарадея при вращении проводника в магнитном поле в нем (в проводнике) возникает ЭДС индукции, которую можно вычислить по следующей формуле: Эта ЭДС и используется для создания тока в цепи (возникает разность потенциалов и, соответственно, начинает течь ток). Как уже видно из формулы – зависимость тока от времени будет иметь синусоидальный характер: Именно такой сигнал (синусоидальный) и используется во всех бытовых цепях переменного тока. Давайте поподробнее остановимся на основных параметрах, а заодно рассмотрим основные формулы и зависимости. На этом рисунке изображено два сигнала (красный и синий 🙂 ). Отличаются они только одним параметром – а именно начальной фазой. Начальная фаза – это фаза сигнала в начальный момент времени, то есть при t = 0. При обсуждении генератора мы приняли величину Синий график: Красный график: Для второй формулы Часто для упрощения расчетов принимают начальную фазу равной нулю. Значение Следующий параметр сигнала – циклическая частота переменного тока – Где Среднее значение тока за период можно вычислить следующим образом: Эта формула представляет собой ни что иное как суммирование всех мгновенных значений переменного тока. А поскольку среднее значение синуса за период равно 0, то На этом мы на сегодня и заканчиваем, надеюсь, что статья получилась понятная и окажется полезна для читателей 🙂 В скором времени мы продолжим изучать электронику в рамках нашего нового курса, так что следите за обновлениями и заходите на наш сайт! microtechnics.ru Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока. Действующим илиэффективнымзначением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе. Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянномтокеза время, определяется по формуле. Переменный ток можно считать постоянным только в течение очень малых промежутков времени. Поделим период колебанийна очень большое число малых промежутков времени. Количество теплоты, выделяемое на сопротивленииза время:. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием: . Сила тока в цепи изменяется по синусоидальному закону , тогда . Опуская вычисления, связанные с интегрированием, запишем окончательный результат . Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов (4.28) Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током: (4.29) Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В. Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам: ,. Тогда мгновенное значение мощности, выделяемой на участке цепи, . Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний): . С использованием известной тригонометрической формулы получим . Величину усреднять не нужно, так как она не зависит от времени, следовательно: . За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю , поэтому(4.30) Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим . (4.31) Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением. Например, если участок цепи состоит из одного только активного сопротивления, тои. Если участок цепи содержит только индуктивность или только ёмкость, тои. Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается. Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27). Пример 4.7.К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлениема) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь. Решение.Когда к генератору подключено одно только активное сопротивление, расходуемая мощность (см. формулу (4.30)). Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора: . Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора . В результате средняя расходуемая генератором мощность . Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза. Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора . Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора . Тогда средняя мощность, расходуемая генератором . Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется. studfiles.net а) Активное сопротивление в цепи переменного тока. Рассмотрим цепь переменного тока, в которую включен только резистор сопротивлениемR не обладающий ни индуктивностью, ни ёмкостью (рис.5а). Такая нагрузка называется активной. Единственным результатом прохождения тока в этом случае будет превращение в резисторе энергии электрического тока в тепловую энергию. В этом случае ток через резистор будет определяться законом Ома i = I0sinωt, а напряжение на резисторе – u = I0R·sinωt = U0sinωt. Т.е. ток и напряжение совпадают по фазе. График тока и напряжения, а также векторная диаграмма амплитуд тока и напряжения показаны на рис. 5б и 5в. б) Индуктивное сопротивление в цепи переменного тока. Рассмотрим случай, когда цепь переменного тока содержит только катушку индуктивностью L, ёмкостью С = 0 и с активным сопротивлением R = 0 (рис.6а). Переменное напряжение u = U0cosωt, поданное на концы катушки, вызовет переменный ток. В результате этого возникнет ЭДС самоиндукции , которая в любой момент времени противоположна по направлению и равна по величине, приложенному к катушке напряжениюuL = U0cosωt: . Теперь закон Ома, для рассматриваемого участка примет вид: U0cosωt = 0,откуда = U0cosωt и di = cosωtdt. После интегрирования для тока получим: i = sinωt + const. Очевидно, что постоянная составляющая тока отсутствует, т.е. const = 0. Теперь i = sinωt = cos(ωt – 900) = I0 cos(ωt – 900). Откуда следует, что , где- индуктивное сопротивление катушки. Оно увеличивается с ростом частоты переменного тока. . Как видно из волновой и векторной диаграмм (рис.6 б,в), в цепи с чисто индуктивным сопротивлением, ток в катушке отстаёт по фазе от напряжения на π/2 радиан. в) Емкостное сопротивление в цепи переменного тока. Рассмотрим случай, когда в цепь включен только конденсатор С (рис.7а) Сопротивление и индуктивность подводящих проводов примем равными нулю. Мгновенное значение напряжения на конденсаторе можно выразить формулойuс=q/C, гдеq– величина заряда на обкладках конденсатора в данный момент времени. Так как всё внешнее напряжениеu=U0cosωtприложено к конденсатору тоuс ==U0cosωt. Откуда q =CU0cosωt. Производная от q поtдаёт силу токаiв цепи:i== – ωCU0sinωt=I0cos(ωt+ 900), гдеI0 = ωCU0= – амплитудное значение силы тока в цепи. Отсюда видно, что выражениеопределяет сопротивление, которое оказывает переменному току конденсатор. Ёмкостное сопротивление уменьшается с ростом частоты. [ХC] = Ом. В цепи с чисто емкостным сопротивлением напряжение, приложенное к обкладкам конденсатора, отстаёт по фазе от тока на π/2 радиан. Это показано на волновой и векторной диаграммах (рис.7 б, в). Рассмотрим цепь, состоящую из резистораR, катушки индуктивности L и конденсатора C (рис.7а). Подадим на концы этой цепи переменное напряжение u = U0cosωt. В цепи возникнет переменный ток той же частоты ω, амплитудой I0и фазой φ, значение которой будет определяться параметрами цепи: сопротивлениемR, индуктивностью L и электроёмкостью С. Этот ток вызовет падения напряжений на отдельных элементах участка цепи – U0,R,U0,C,U0,L.Поскольку соединение последовательное, то результирующее напряжениеU0 будет определяться векторной суммой напряжений на отдельных элементах (рис.7б). По теореме Пифагора получим: . (14) Закон Ома для данной цепи запишется так: , (15) где – полное сопротивление или импеданс цепи переменного тока. Треугольник сопротивлений представлен на рис. 8. Разность фаз между токомI и напряжением U определяется углом φ между векторами U0 и I0. Из диаграммы (рис.8) следует: . (16) Из формулы для Z вытекает, что чем ближе по величине и 1/ωС, тем меньше полное сопротивлениеZ и тем больше ток в цепи. При ωL = 1/ωC угол сдвига фаз обращается в нуль (φ = 0), полное сопротивление Z = R и ток достигает максимального значения: I0,max = U0,рез/ R. (17) Это явление называется резонансом напряжения. Для цепи с заданными L и C, резонанс имеет место при частоте . РАБОТА И МОЩНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА Мгновенное значение мощности р(t) переменного тока равно произведению мгновенных значений напряжения u(t) =U0cosωtи силы токаi(t) = I0cos(ωt– φ): р(t) = U0cosωtI0 cos(ωt – 900) = I0U0 cosωt cos(ωt – 900).() Воспользовавшись формулой получим: . Практический интерес представляет среднее по времени значение мощности Р. Т.к. среднее значение cos(2ωt- φ) равно нулю, то .() Из векторной диаграммы рис. 7б следует, что U0 cosφ= RI0. Поэтому. Такую же мощность развивает постоянный ток, силой. Это значение называется действующим (или эффективным) значением силы переменного тока. Аналогично величинаназывается действующим (или эффективным) значением напряжения. С использованием действующих (или эффективных) значений тока и напряжения Р =U0 I0cosφ.Множительcosφназывается коэффициентом мощности. Как видно из диаграммы рис. 7б, при равенстве реактивных значений сопротивлений ХC= ХLмножительcosφ= 1 (φ = 0) Р =U0 I0, т.е. выделяющаяся в цепи мощность имеет максимальное значение. При чисто реактивном сопротивлении цепи (R= 0) мощность, выделяемая в цепи, равна нулю. По этой причине на практике электрическую цепь переменного тока стремятся сбалансировать так чтобы значения реактивных сопротивлений ХCи ХLбыли как можно ближе. Для промышленных установок наименьшее допустимое значениеcosφ= 0,85. или. (48) Работа за период T: . (49) Средняя мощность переменного тока . (50) Обозначим , откуда эффективный (действующий) ток -.(51) Тогда . (52) Из сравнения соотношений (47) и (52) следует, что эффективная сила переменного равна силе такого постоянного тока, который имеет ту же мощность, что и данный переменный ток. Если в цепи переменного тока имеются реактивные сопротивления, то мощность: (53) (на основании тригонометрического тождества: ). Среднее значение мощности NСза период Т, а, следовательно, и за любой промежуток времениt>>T, равно разности средних значений. Но первый член есть постоянная величина, не зависящая от времени, а второй – периодическая функция, среднее значение которой за периодTравна нулю. Таким образом,(54) или (55) Множитель называется коэффициентом мощности электрической цепи. ЕслиR=0, тоиNC=0. Энергия, которая поступает в цепь от источника за T/2, возвращается источнику в течение следующей половины периода. Следовательно, для повышения мощности, отдаваемой переменным током в цепь, необходимо добиться повышенияпутём включения в цепь такихRLиRCнагрузок, которые соответствуют условию резонанса (45). ПРИРОДА ЕМКОСТНЫХ СВОЙСТВ ТКАНЕЙ ОРГАНИЗМА studfiles.net Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока. Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации. Переменный ток, меняет свое значение и направление, определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебательное движение. Вследствие своей малой скорости движения (Vэл= 10-4м/с = 0,1 мм/с) электроныпри таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода. Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, ЭДС) со временем показывает плавная кривая линия, называемая синусоидой). Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока. Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии. Кроме того, именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы, входящие в состав электрических цепей не изменяют синусоидальной формы тока и напряжения. Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются: во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности; во-вторых, тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения. Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется. Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи. Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений: сдвиг фаз, явление резонанса, появление реактивных мощностей. На современных промышленных предприятиях большинство потребителей электрической энергии переменного тока представляют собой активно-индуктивную нагрузку в виде асинхронных электродвигателей, силовых трансформаторов, сварочных трансформаторов, преобразователей и так далее. В такой нагрузке в результате протекания переменного тока индуктируются ЭДСсамоиндукции, обуславливающие сдвиг по фазе между током и напряжением. Этот сдвиг по фазе обычно увеличивается, аcos уменьшается при малой нагрузке. Например, еслиcos двигателей переменного тока при полной нагрузке составляет 0,75 - 0,8, то при малой нагрузке он уменьшается до 0,2 - 0,4. Если мощность, потребляемая всеми приемниками в данных цепях, является вполне определенной, то при неизменном напряжении на зажимах приемника их ток: I = P / (Ucos ) С уменьшением cos ток нагрузки электростанций и подстанций будет увеличиваться при одной и той же отдаваемой мощности. Вместе с тем электрические генераторы, трансформаторы и линии электропередачи рассчитываются на определенное напряжение и ток. Увеличение тока потребителя при снижении cosне должно превышать определенных пределов, так как питающие их генераторы рассчитываются на определенную номинальную мощностьSном = Uном Iном, вследствие чего они не должны оказаться перегруженными. Для того чтобы ток генератора не превышал номинального значения при сниженииcos потребителя, необходимо снижать его активную мощность. Таким образом, понижениеcos потребителей вызывает неполное использование мощности синхронных генераторов, трансформаторов и линий электропередачи. Они бесполезно загружаются за счет индуктивного реактивного тока. cos, характеризующий использование установленной мощности, часто называют коэффициентом мощности. Коэффициентом мощности определяют как отношение активной мощности к полной: cos = P/S. (2.71) 2.25 Коэффициент мощности (Адрес Блок 4) Коэффициентом мощности определяют как отношение активной мощности к полной:cos = P/S. Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. Коэффициент мощности (2.25)показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. Нормальным считаетсяcos 0,85 - 0,9. При низком коэффициенте мощности на предприятия, потребляющие электроэнергию, накладывается штраф, при высоком - предприятия премируются. Для улучшения коэффициента мощности проводится ряд мероприятий: 2.заменяются двигатели переменного тока, нагруженные относительно мало, двигателями меньшей мощности; 2.включаются параллельно приемникам конденсаторы. studfiles.net Переменный ток Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток. Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток. Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника или Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону. Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ωпо синусоидальному или косинусоидальному закону: u=Um⋅sinωt u=Um⋅sinωt или u=Um⋅cosωt u=Um⋅cosωt , где u – мгновенное значение напряжения, Um – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае i=Im⋅sin(ωt+φc) i=Im⋅sin(ωt+φc) , где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения. Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц. Резистор в цепи переменного тока Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление Rназывается активным потому, что, только на нем выделяется энергия, т.е. Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением. Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1). Рис. 1 Пусть напряжение на концах цепи меняется по гармоническому закону u=Um⋅sinωt u=Um⋅sinωt . Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома: i=UR=Um⋅sinωtR=Im⋅sinωt i=UR=Um⋅sinωtR=Im⋅sinωt . Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление: Рис. 2 При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока. Применение: Постоянный ток широко используется в технике: подавляющее большинство электронных схем в качестве питания используют постоянный ток. Переменный ток используется преимущественно для более удобной передачи от генератора до потребителя. Иногда в некоторых устройствах постоянный ток преобразуют в переменный ток преобразователями (инверторами). ЗАКОНЫ ПОСТОЯННОГО ТОКА Всякое движение электрических зарядов называют электрическим током. В металлах могут свободно перемещаться электроны, в проводящих растворах - ионы, в газах могут существовать в подвижном состоянии и электроны, и ионы. Условно за направление тока считают направление движения положительных частиц, поэтому металлахнаправление тивоположно направлению движения электронов. Плотность тока - величина заряда, проходящего в единицу времени через единицу поверхности, перпендикулярной к линиям тока. Эта величина обозначается j и рассчитывается следующим образом: j=nev. Здесь n - концентация заряженных частиц, e - заряд каждой из частиц, v - их скорость. Сила тока i - величина заряда, проходящего в единицу времени через полное сечение проводника. Если за время dt через полное сечение проводника прошел заряд dq, то i=(dq)/(dt). По другому, сила тока находится интегрированием плотности тока по всей поверхности любого сечения проводника. Единица измерения силы тока - Ампер. Если состояние проводника (его температура и др.) стабильно, то между приложенным к его концам напряжением и возникающим при этом током существует однозначная связь. Она называется Закон Ома и записывается так: I=U/R. R - электрическое сопротивление проводника, зависящее от рода вещества и от его геометрических размеров. Единичным сопротивлением обладает проводник, в котором возникает ток 1 А при напряжении 1 В. Эта единица сопротивления называется Ом. Закон Ома в дифференциальной форме: j=sE, где j - плотность тока, Е - напряженность поля, - проводимость. В этой записи закон Ома содержит величины, характеризующие состояние поля в одной и той же точке. Различают последовательное и параллельное соединения проводников.При последовательном соединении ток, протекающий по всем участкам цепи, одинаков, а напряжение на концах цепи складывается как алгебраическая сумма напряжений на всех участках R=S(Ri). При параллельном соединении проводников постоянным остается напряжение, а ток складывается из суммы токов, протекающих по всем ветвям. В этом случае складываются величины, обратные сопротивлению: 1/R=S(1/Ri) Для получения постоянного тока на заряды в электрической цепи должны действовать силы, отличные от сил электростатического поля; их называют сторонними силами. Если рассматривать полную электрическую цепь, необходимо включить в нее действие этих сторонних сил и внутренне сопротивление источника тока r. В этом случае закон Ома для полной цепи примет вид I=E/(R+r) Е - электродвижущая сила (ЭДС) источника. Она измеряется в тех же единицах, что и напряжение. Величину (R+r) называют иногда полным сопротивлением цепи. Сформулируем правила Киркгофа: Первое правило: алгебраическая сумма сил токов в участках цепи, сходящихся в одной точке разветвления, равна нулю. Второе правило: для любого замкнутого контура сумма всех падений напряжения равна сумме всех ЭДС в этом контуре. Мощность тока рассчитывается по формуле P=UI=I2R=U2/R. Закон Джоуля-Ленца. Работа электрического тока (тепловое действие тока) A=Q=UIt=I2Rt=U2t/R. Электрический ток в металлах есть движение электронов, ионы металла участия в переносе электрического заряда не принимают. Другими словами, в металлах есть электроны, способные перемещаться по металлу. Они получили название электронов проводимости. Положительные заряды в металле представляют собой ионы, образующие кристаллическую решетку. В отсутствии внешнего поля электроны в металле движутся хаотично, претерпевая соударения с ионами решетки. Под воздействием внешнего электрического поля электроны начинают упорядоченное движение, накладывающееся на их прежние хаотические флуктуации. В процессе упорядоченного движения электроны по-прежнему сталкиваются с ионами кристаллической решетки. Именно этим и обусловлено электрическое сопротивление. В классической электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики. Взаимодействием электронов между собой пренебрегают, взаимодействие электронов с ионами сводят только к соударениям. Можно сказать, что электроны проводимости рассматривают как электронный газ, подобный идеальному атомарному газу в молекулярной физике. Поскольку средняя кинетическая энергия на одну степень свободы для такого газа равна kT/2, а свободный электрон обладает тремя степенями свободы, то mv2t/2=3kT/2, где v2t - среднее значение квадрата скорости теплового движения.На каждый электрон действует сила, равная еЕ, в результате чего он приобретает ускорение еЕ/m. Скорость к концу свободного пробега равна v=eEt/m, где t - среднее время между соударениями. Поскольку электрон движется равноускоренно, его средняя скорость равна половине максимальной: vc=eEt/(2m) Среднее время между соударениями есть отношение длины свободного пробега к средней скорости: t=L/vt. Поскольку обычно скорость упорядоченного движения много меньше тепловой скорости, то скоростью упорядоченного движения пренебрегли. Окончательно, имеем vc=eEL/(2mvt). Коэффициент пропорциональности между vc и Е называется подвижность электронов. С помощью классической электронной теории газов могут быть объяснены многие закономерности - закон Ома, закон Джоуля-Ленца и другие явления, однако эта теория не может объяснить, например, явления сверхпроводимости: При определенной температуре удельное сопротивление для некоторых веществ скачком уменьшается практически до нуля. Это сопротивление настолько мало, что однажды возбужденный в сверхпроводнике электрический ток существует длительное время без источника тока. Несмотря на скачкообразное изменение сопротивления, другие характеристики сверхпроводника (теплопроводность, теплоемкость и др.) не меняются либо меняются мало. Более точным методом, объясняющим такие явления в металлах, является подход с использованием квантовой статистики. Электрический ток в газах В обычном состоянии газы не проводят электричества. Однако под влиянием различных внешних факторов (высокая температура, различные излучения) газы становятся электропроводящими. Это происходит вследствие того, что от нейтральных атомов отделяются электроны и образуются проводящие частицы - положительные ионы и свободные электроны. Часть свободных электронов может быть захвачена нейтральными атомами и образуются отрицательные ионы. Этот процесс называется ионизацией. Ионизация атома (отрыв электрона) требует определенной энергии, величина которой зависит от строения атома и называется энергией ионизации. Если ионизацию не поддерживать, например, бомбардируя атомы электронами, ускоренными во внешнем электрическом поле, то со временем происходит рекомбинация ионов - положительный и отрицательный ион в результате теплового движения сталкиваются и избыточный электрон переходит к положительному иону. В результате образуется два нейтральных атома. Рассмотрим принципиальную схему, изображенную на рисунке: Пусть на отрицательный электрод падают ультрафиолетовые лучи, обеспечивающие ионизацию газа. Если увеличивать напряжение между электродами (например, плавно уменьшая сопротивление r) то сила тока будет увеличиваться, пока не достигнет максимума (тока насыщения), при котором все свободные электроны достигают противоположного электрода. Сила тока насыщения зависит только от интенсивности процесса ионизации (в нашем случае, от интенсивности ультрафиолетовых лучей). Если снять внешнюю ионизацию, разряд между электродами исчезнет. Такие разряды называются несамостоятельными. Если же продолжать уменьшать сопротивление (увеличивая тем самым напряжение) произойдет резкое (в сотни раз) увеличение силы тока, в газе появятся световые и тепловые эффекты. Если прекратить действие ионизатора, то разряд будет продолжаться. Это значит, что новые ионы для поддержания разряда образуются благодаря процессам в самом разряде. Такие разряды называют самостоятельными. Дело в том, что с увеличением напряжения возрастает скорость и кинетическая энергия электрона, и он при столкновении с атомом сам способен произвести его ионизацию - высвободить еще один электрон. На следующем этапе два электрона образуют уже четыре и т.д. Происходит лавинообразное увеличение количества носителей. Это явление получило название электронной (или ионной) лавины, а напряжение, при котором это происходит - напряжением пробоя газового промежутка (напряжением зажигания газового разряда). В зависимости от свойств и внешнего вида разрядов различают коронный, искровой, дуговой, тлеющий и другие разряды. В различных формах газового разряда иногда образуется сильно ионизированный газ, в котором концентрация электронов приблизительно равна концентрации положительных ионов. Такая система получила название ионной плазмы. Ток в вакууме Как известно, в металлах имеются электроны проводимости, образующие "электронный газ" и участвующие в тепловом движении. Для того, чтобы свободный электрон мог выйти из металла, должна быть совершена определенная работа, различная для разных металлов и названная работой выхода. Существование работы выхода показывает, что в поверхностном слое металла существует электрическое поле, значит, электрический потенциал при переходе через этот слой изменяется на некоторую величину, также специфичную для разных металлов. Эта поверхностная разность потенциалов связана с работой выхода соотношением: A=ef Поскольку выйти из металла могут только "самые быстрые" электроны, то можно записать условие выхода так mv2/2>ef В обычных условиях работа выхода в сотни раз больше энергии теплового движения электронов, поэтому подавляющее большинство их остается в металле. Но если сообщить электронам дополнительную энергию, можно наблюдать явление испускания электронов или электронной эмиссии. В зависимости от того, каким образом сообщена дополнительная энергия, различают термоэлектронную эмиссию, фотоэмиссию, вторичную электронную эмиссию и др. Для наблюдения термоэлектронной эмиссии используется принципиальная схема, содержащая вакуумный диод (см. рис.). В такой цепи возникнет ток, только если катод раскалить до высокой температуры. Вольт-амперная характеристика диода показывает, что при нулевой разности потенциалов ток очень мал. В дальнейшем, при увеличении потенциала на аноде, увеличивается и ток, пока не достигнет некоторого постоянного значения - тока насыщения Is. Его значение увеличивается с увеличением температуры катода. Также с увеличением температуры растет и напряжение Us, при котором достигается ток насыщения. По графику наглядно видно, что зависимость между током и напряжением для диода носит нелинейный характер, то есть диод не подчиняется закону Ома. Богуславский и Лэнгмюр независимо друг от друга показали, что зависимость тока диода от потенциала анода имеет вид: I=CU3/2 Где С зависит от формы и размеров электродов. Зависимость плотности тока насыщения от температуры известна под названием формулы Ричардсона:Js=CT1/2exp(-ef/kT), где С - константа, различная для разных металлов. Эта формула выведена на основании классической электронной теории. Квантовая теория металлов дает следующее соотношение:Js=АT2exp(-ef/kT) Заметим, что это различие не существенно, так как зависимость плотности тока от температуры определяется главным образом экспоненциальным множителем exp(-e/kT). Соединение в звезду На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода. Линейнымназывается провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной(на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки). Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным(на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной,с нейтральным проводом – четырехпроводной. Все величины, относящиеся к фазам, носят название фазных переменных,к линии - линейных.Как видно из схемы на рис. 6, при соединении в звезду линейные токи Если система фазных токов симметрична, то Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать Отметим, что всегда На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае Обычно при расчетах принимается 3. Соединение источника энергии и приемника по схеме треугольник.В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8). Для симметричной системы ЭДС имеем Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9. Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями Аналогично можно выразить линейные токи через фазные токи генератора. На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов Помимо рассмотренных соединений «звезда - звезда» и «треугольник - треугольник» на практике также применяются схемы «звезда - треугольник» и «треугольник - звезда». Явление резонанса Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением. Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии. Для определения условий возникновения режима резонанса в электрической цепи нужно: найти ее комплексное сопротивление или проводимость; выделить мнимую часть и приравнять нулю. Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса. Уравнение Im[Z]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл. В электрических цепях резонанс может рассматриваться в задачах: анализа этого явления при вариации параметров цепи; синтеза цепи с заданными резонансными параметрами. Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами. Сдвиг фаз между током и напряжением. Понятие двухполюсника Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром. Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников. Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно Условием резонанса из выражения (1) будет Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление xL = wL равно емкостному xC = 1/(wC) . Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров - L, C и w , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в последовательном контуре можно создать изменением индуктивности L при постоянных значениях C и w ; изменением емкости C при постоянных значениях L и w ; изменением частоты w при постоянных значениях L и C. Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии. При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Zmin = R , j = 0 , т.е. полное сопротивление при резонансе соответствует минимальному значению. Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю xC®µ , xL® 0 , и j® - 90° (рис. 1 б)). При бесконечном увеличении частоты - xL®µ , xC ® 0 , а j® 90° . Равенство сопротивлений xLи xC наступает в режиме резонанса при частоте w0 . Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i=Imsinwt. Падение напряжения на входе уравновешивается суммой напряжений на элементах Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура а при резонансной частоте где величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура. Следовательно, при резонансе напряжение на резисторе равно напряжению на входе контура; напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура; соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений. Отношение волнового сопротивления к резистивному r /R = Q, называется добротностью контура, а величина обратная D=1/Q - затуханием. Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений. Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем в выражениях (5) к относительным единицам, разделив их на входное напряжение при резонансе U=RI0 где i =I/I0, uk=Uk/U, v = w /w0 - соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I0, напряжение на входе U и частота w0 в режиме резонанса. Абсолютный и относительный ток в контуре равен Из выражений (7) и (8) следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q=2 приведено на рис. 3 в логарифмическом (а) и линейном (б) масштабах оси абсцисс. На рис. 3 кривые A(v), B(v) и C(v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A(v)=uL(v) и B(v)=uC(v) имеют максимумы, напряжения в которых определяются выражением а относительные частоты максимумов равны При увеличении добротности Q ®µAmax = Bmax®Q, С уменьшением добротности максимумы кривых uL(v ) и uС(v ) смещаются от резонансной частоты, а при Q2 < 1/2 исчезают, и кривые относительных напряжений становятся монотонными. Напряжение на резисторе и ток в контуре имеют при резонансной частоте максимум равный 1,0. Если на оси ординат отложить абсолютные значения тока или напряжения на резисторе, то для различных значений добротности они будут иметь вид, показанный на рис. 4. В целом они дают представлние о характере изменения величин, но удобнее делать сопоставление в относительных единицах. На рис. 5 представлены кривые рис. 4 в относительных единицах. Здесь видно, что увеличение добротности влияет на скорость изменения тока при изменении частоты. Можно показать, что разность относительных частот, соответствующих значениям относительного тока Перейдем теперь к анализу зависимости фазового сдвига между током и напряжением на входе контура от частоты. Из выражения (1) угоj j равен Как и следовало ожидать, значение j определяется добротностью контура. Графически эта зависимость для двух значений добротности показана на рис. 6 . При уменьшении частоты значение фазового сдвига стремится к значению - 90° , а при увеличении к +90° , проходя через нулевое значение при частоте резонанса. Скорость изменения функции j (v ) определяется добротностью контура. Последовательный резонансный контур может питаться также от источника электрической энергии, обладающего свойствами источника тока, т.е. обеспечивающего постоянный ток в нагрузке. Выражения (5) остаются справедливыми и в этом случае, но ток в них будет константой. Поэтому постоянным будет падение напряжения на резисторе UR = RI = const. Разделив все напряжения на это базовое значение, Общее относительное падение напряжения на входе контура является гипотенузой прямоугольного еугольника напряжений, поэтому Для функции u (v )=С(v ) можно показать, что разность относительных частот v1 и v2 , соответствующих значениям Фазовые характеристики контура при питании от источника тока ничем не отличаются от характеристик режима питания от источника ЭДС (рис. 6). Сопоставляя частотные характеристики при питании последовательного резонансного контура от источника тока с характеристиками при питании его от источника ЭДС, можно сделать следующие выводы: частотные характеристики напряжений и тока контура принципиально отличаются друг от друга, т.к. при питании от источника ЭДС сумма напряжений остается постоянной и происходит только их перераспределение между элементами, а при питании от источника тока падения напряжения на каждом элементе формируются независимо; режимы резонанса для обоих случаев полностью идентичны; фазовые частотные характеристики для обоих случаев также идентичны. Режим резонанса можно создать также при параллельном соединении R, L и C (рис. 8а)). Такая цепь называется параллельным резонансным контуром. В этом случае условие резонанса удобнее сформулировать для мнимой части комплексной проводимости в виде Следовательно, для параллельного контура возможны те же вариации параметров, что и для последовательного и выражения для них будут идентичным При изменении частоты питания изменяется только мнимая составляющая вектора комплексной проводимости Y , поэтому его конец перемещается на комплексной плоскости по прямой параллельной мнимой оси и проходящей через точку G=1/R , соответствующую вещественной составляющей проводимости (рис. 8 б)). При частоте резонанса модуль вектора минимален, а при стремлении частоты к нулю и бесконечности, его значение стремится к бесконечности. При этом угол сдвига фаз между током и напряжением j на входе контура стремится к 90° при w® 0 и к - 90° при w®µ . Для параллельного соединения токи в отдельных элементах можно представить через проводимости и общее падение напряжения U в витщ где волновая или характеристическая проводимость контура. Как следует из выражений (17), при резонансе токи в реактивных элементах одинаковы, а входной ток равен току в резисторе R. Отношение Q=g /G называется добротностью, а величина обратная D=1/Q - затуханием параллельного резонансного контура. Таким образом, добротность равна отношению токов в реактивных элементах контура к току на входе или в резисторе. В электрических цепях добротность может достигать значений в несколько десятков единиц и во столько же раз токи в индуктивности и емкости будут превышать входной ток. Поэтому резонанс в параллельном контуре называется резонансом токов. Падение напряжения на входе контура U при питании его от источника, обладающего свойствами источника тока и формирующего ток с действующим значением I, будет равно lektsia.com Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1): Рис.1. Вращающийся вектор С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно, имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно, и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат) и тогда и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно, Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно. 2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2) Рис.2. Комплексное число на комплексной плоскости Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна На рисунке выше этот вектор также показан.Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.Итак, три формы записи комплексного числа: 1) показательная форма в виде 2) тригонометрическая форма в виде 3) алгебраическая форма где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая. Например, имеем комплексное число в показательной форме вида в тригонометрической форме записи это запишется как при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что В итоге получим где При переходе от алгебраической формы к показательной комплексное число вида переходит к показательному виду по следующим преобразованиям а угол Таким образом, и получим Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода: Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи. Рис.3. Схема с последовательным соединением элементов Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4): Рис.4. Схема с комплексными обозначениями По закону Ома ток в цепи равен где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида Соответственно, комплекс входного напряжения в показательной форме запишется как Полное комплексное сопротивление цепи в общем виде Находим комплексное сопротивление индуктивности Находим комплексное сопротивление емкости Соответственно, общее комплексное сопротивление цепи Ток в цепи Комплексные напряжения на элементах Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство Проверяем С небольшим расхождением из-за округлений промежуточных вычислений всё верно. Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:1) полное сопротивление электрической цепи и его характер;2) действующие значения токов в ветвях;3) показания вольтметра и ваттметра; Рис.5.Цепь однофвзного синусоидального тока Решение:1. Находим комплексные сопротивления ветвей и всей цепи:Учитываем, что Комплексное сопротивление первой ветви: Комплексное сопротивление второй ветви: Комплексное сопротивление третьей ветви: Общее сопротивление цепи Откуда 2. Находим действующие значения токов в ветвях: Рис.6. Схема с обозначенными комплексными токами Действующие значения, соответственно, 3. Определим показания приборов:Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:U=220 ВВаттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания: electrikam.com Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него. Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы). В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю. Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю. Тогда, падение напряжения на активном сопротивлении определяется по формуле: где, U-напряжение на элементе цепи, I – ток через элемент цепи R – активное сопротивление элемента Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения: где, Um-амплитудное значение напряжения на элементе цепи, Im – амплитудное значение тока через элемент цепи R – активное сопротивление элемента В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3). Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов. Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов. Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения. Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам: где — UL-падение напряжение на чисто индуктивном сопротивлении ; UС—падение напряжения на чисто емкостном сопротивлении; I— значение тока в через реактивное сопротивление; L— индуктивность реактивного элемента; C— емкость реактивного элемента; ω— циклическая частота. Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов. Приведенные выше формулы являются частными случаями закона Ома для переменного тока. Следовательно, полный закон Ома для переменного тока будет иметь вид: Где Z – полное сопротивление цепи переменного тока. Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены. Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.) Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления. Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой: где —эффективное значение силы тока в А; U—эффективное значение напряжения в В; R—активное сопротивление в Ом; ωL—индуктивное сопротивление в ом. Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения. В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления. Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления. А закон Ома для такой цепи принимает вид: В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6), Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления. Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так: где I-сила тока в А; U-напряжение в В; R-активное сопротивление в Ом; ωL-индуктивное сопротивление в Ом; 1/ωС-емкостное сопротивление в Ом. Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения. Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5). Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) - параллельное соединение R и L; б) - параллельное соединение R и C. Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8. Рисунок 8. Эквивалентная схема колебательного контура. Таким образом закон Ома для переменного тока можно сформулировать следующим образом. Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи) ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! www.sxemotehnika.ru3.2 Виды нагрузок в цепи переменного тока. Напряжение в цепи переменного тока
Переменный ток. Цепи переменного тока.

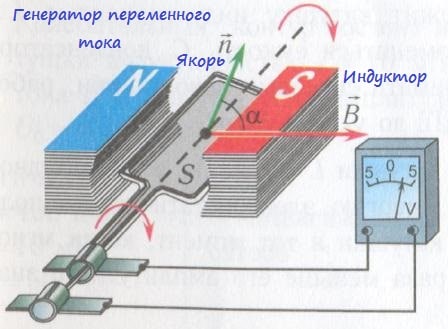
Генератор переменного тока.
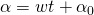
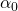 – это угол в начальный момент времени (t = 0). Примем его равным 0, таким образом:
– это угол в начальный момент времени (t = 0). Примем его равным 0, таким образом: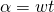
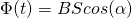
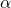 зависит от времени.
зависит от времени.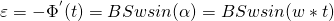
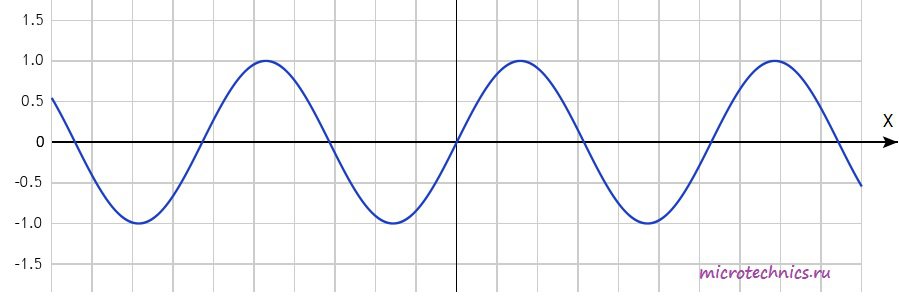
Основные параметры синусоидального сигнала.
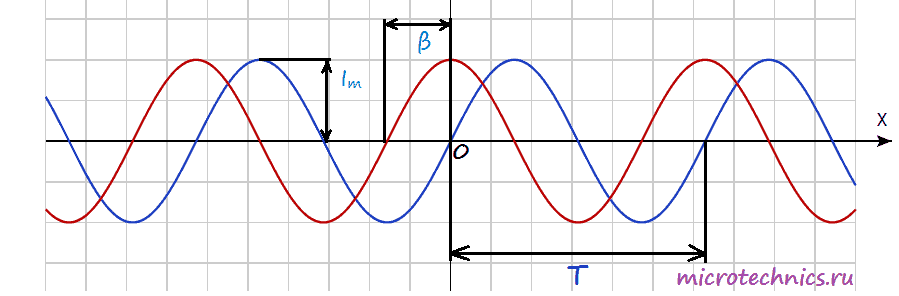
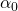 равной нулю, так вот это и есть начальная фаза. Для данных графиков уравнения выглядят следующим образом:
равной нулю, так вот это и есть начальная фаза. Для данных графиков уравнения выглядят следующим образом: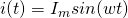
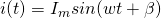
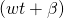 это фаза переменного тока, а
это фаза переменного тока, а 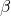 – это начальная фаза.
– это начальная фаза.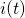 в любой момент времени называют мгновенным значением переменного тока. Вообще все эти термины справедливы для любых гармонических сигналов, но раз уж мы обсуждаем переменный ток, то будем придерживаться этой терминологии 🙂 Максимальное значение функции
в любой момент времени называют мгновенным значением переменного тока. Вообще все эти термины справедливы для любых гармонических сигналов, но раз уж мы обсуждаем переменный ток, то будем придерживаться этой терминологии 🙂 Максимальное значение функции 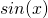 равно 1, соответственно, максимальная величина тока в нашем случае будет равна
равно 1, соответственно, максимальная величина тока в нашем случае будет равна 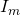 – амплитудному значению.
– амплитудному значению.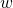 – она, в свою очередь, определяется следующим образом:
– она, в свою очередь, определяется следующим образом: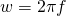
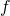 – частота переменного тока. Для привычных нам сетей 220 В частота равна 50 Гц (это значит, что 50 периодов сигнала укладываются в 1 секунду). А период сигнала равен:
– частота переменного тока. Для привычных нам сетей 220 В частота равна 50 Гц (это значит, что 50 периодов сигнала укладываются в 1 секунду). А период сигнала равен: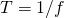 .
.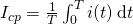
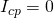 .
.4.4.4. Эффективные напряжение и ток
4.4.5. Мощность в цепи переменного тока
3.2 Виды нагрузок в цепи переменного тока
4.Импеданс цепи переменного тока с последовательным включением резистора, катушки и конденсатора. Резонанс напряжений
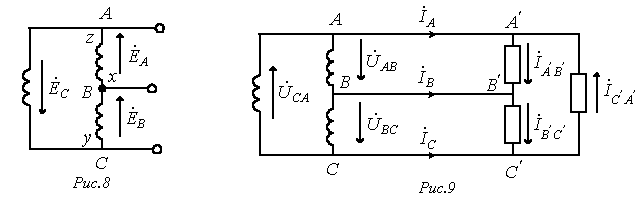
Электрические цепи переменного тока
Коэффициент мощности.
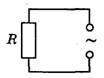
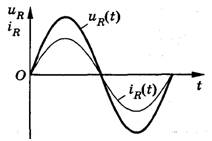
Резистор в цепи переменного тока
 и
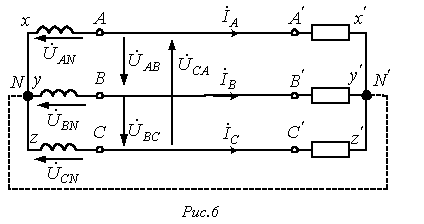
и  равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе
равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе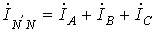 .
.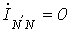 . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
. Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.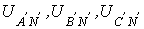 - фазные напряжения нагрузки.
- фазные напряжения нагрузки.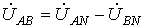 ; (1)
; (1)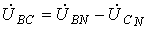 ; (2)
; (2)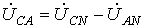 . (3)
. (3)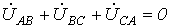 - как сумма напряжений по замкнутому контуру.
- как сумма напряжений по замкнутому контуру.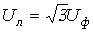 (4)
(4)
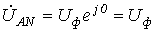 . Тогда для случая прямого чередования фаз
. Тогда для случая прямого чередования фаз 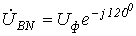 ,
, 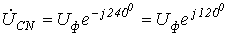 (при обратном чередовании фазфазовые сдвиги у
(при обратном чередовании фазфазовые сдвиги у 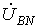 и
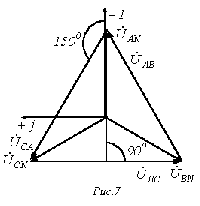
и 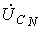 меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору
меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору 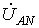 (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений
(его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений 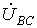 и
и 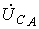 получаем:
получаем: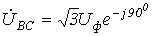 ;
;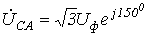 .
.
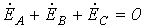 .
.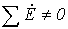 и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.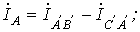
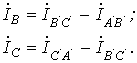
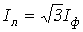 . (5)
. (5)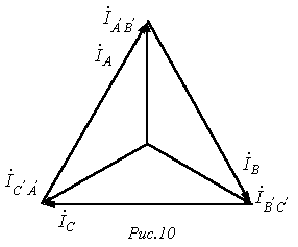
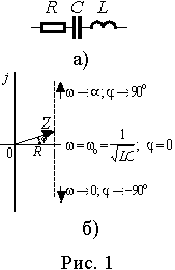
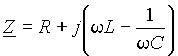
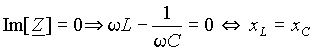
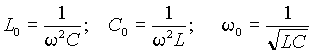
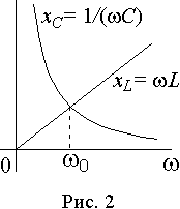
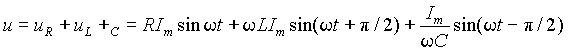
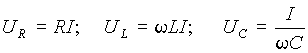
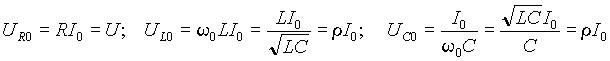
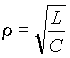
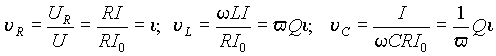
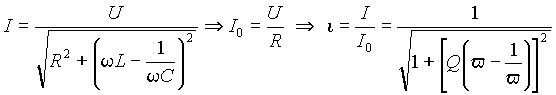
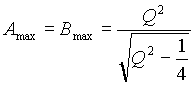 , (9)
, (9)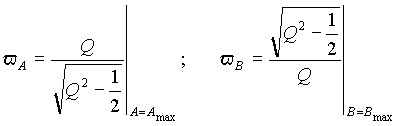 (10)
(10)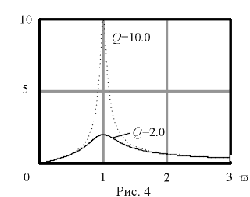
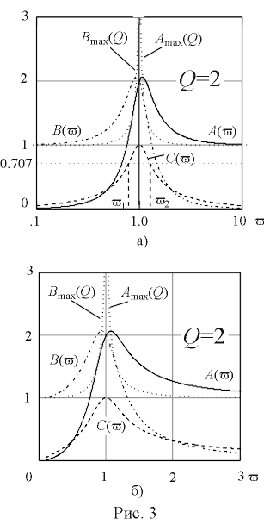
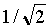 , равна затуханию контура D=1/Q =v2-v1.
, равна затуханию контура D=1/Q =v2-v1.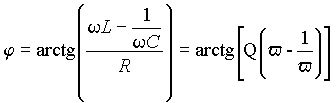
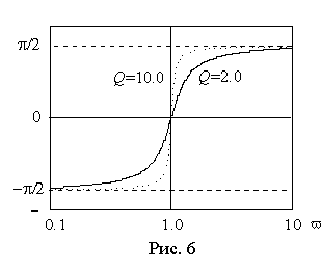
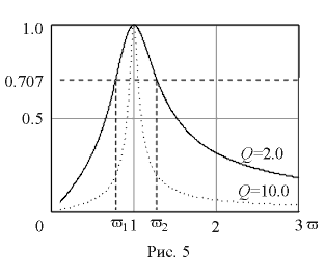
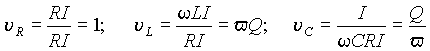 В выражении (12) добротность также есть отношение волнового сопротивления к резистивному Q=r /R .
В выражении (12) добротность также есть отношение волнового сопротивления к резистивному Q=r /R .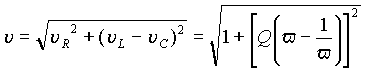 Функции uL(v ) и uС(v ) монотонны, а u(v ) имеет минимум u =1.0 при резонансной частоте, когда uL(v ) -uС(v ) = 0. В случае стремления относительной частоты к бесконечности и к нулю, напряжения на одном из реактивных элементов стремится к бесконечности. При резонансной частоте они одинаковы и их отношение ко входному напряжению равно добротности.
Функции uL(v ) и uС(v ) монотонны, а u(v ) имеет минимум u =1.0 при резонансной частоте, когда uL(v ) -uС(v ) = 0. В случае стремления относительной частоты к бесконечности и к нулю, напряжения на одном из реактивных элементов стремится к бесконечности. При резонансной частоте они одинаковы и их отношение ко входному напряжению равно добротности.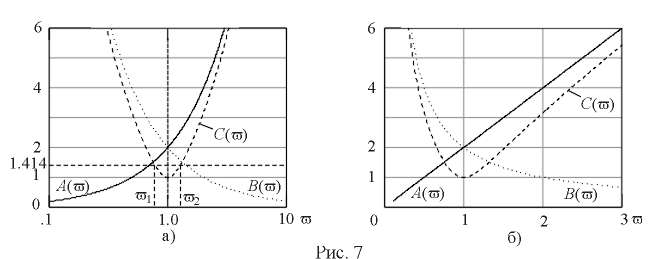 Графическое представление функций uL(v )=A(v ), uС(v )=B(v ) и u(v )=С(v ) при добротности Q=2 дано на рис. 7 в логарифмическом (а) и линейном (б) масштабах оси частот.
Графическое представление функций uL(v )=A(v ), uС(v )=B(v ) и u(v )=С(v ) при добротности Q=2 дано на рис. 7 в логарифмическом (а) и линейном (б) масштабах оси частот.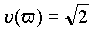 , равна затуханию контура D=1/Q=v2-v1.
, равна затуханию контура D=1/Q=v2-v1.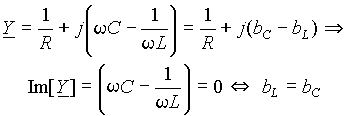
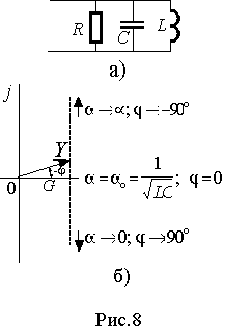
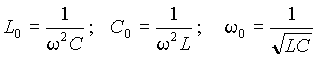 900+
900+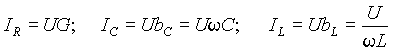 Пусть в режиме резонанса падение напряжения на входе контура равно U0, тогда токи в отдельных элементах будут
Пусть в режиме резонанса падение напряжения на входе контура равно U0, тогда токи в отдельных элементах будут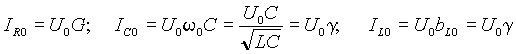
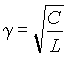
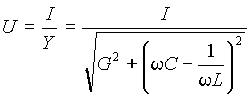
Символический (комплексный) метод расчета цепей переменного тока







 .
.


















 при φ = 0° равно
при φ = 0° равно









Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.







 — нагрузка носит активно-индуктивный характер
— нагрузка носит активно-индуктивный характер



Закон Ома для переменного тока


(1)

(2)



(3)

(4)

(5)
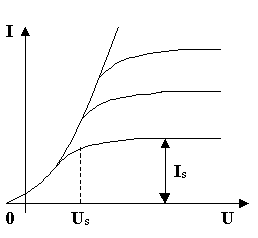
Закон Ома для различных типовых цепей переменного тока


(6)


(7)


(8)


Похожие материалы:
Добавить комментарий
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: