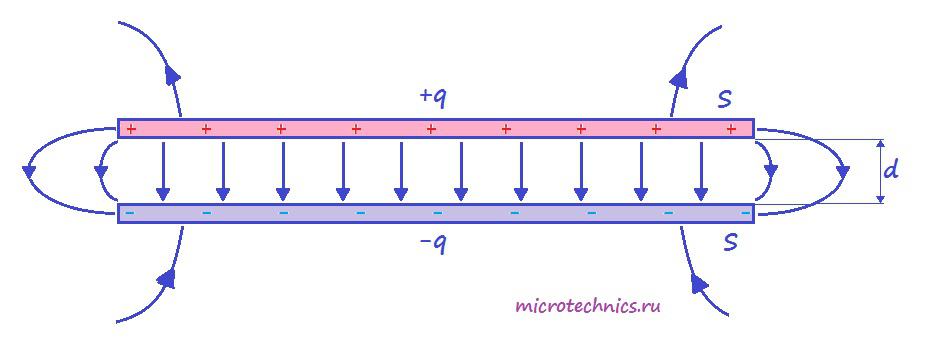
Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье нам предстоит разобраться, из чего они состоят, как работают и для чего применяются 🙂 Давайте, в первую очередь, рассмотрим устройство конденсаторов, а затем уже плавно перейдем к их основным видам и характеристикам, а также к процессам зарядки/разрядки. Как видите, нам сегодня предстоит изучить много интересных моментов 😉 Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин: Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке). А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит 🙂 Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора: Каждая из обкладок конденсатора в отдельности создает электрическое поле: Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом: Здесь Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом: А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂 С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом: Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится. При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом: Как видите, здесь нет ничего сложного 🙂 Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом: Здесь у нас Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить Для запасенной энергии конденсатора справедливы следующие выражения: Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение – то есть величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет. В общем, мы рассмотрели сегодня основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений конденсаторов, так что заходите на наш сайт снова! microtechnics.ru Задача Условие: Плоский конденсатор емкостью С заполнен проводящим диэлектриком с проницаемостью ε и удельным сопротивлением ρ. Расстояние между пластинами равно d. Через резистор сопротивлением R конденсатор подключен к источнику с ЭДС Ɛ и внутренним сопротивлением r. Определите напряженность электрического поля в диэлектрике. Решение:
Материалы, которые обладают обычно диэлектриками, в той или иной степени обладают электропроводностью. Если к источнику постоянного тока подключить конденсатор, заполненный проводящим диэлектриком, в цепи пойдет электрический ток (ток утечки). Между пластинами конденсатора будет существовать электрическое поле, напряженность которого Е можно определить, зная напряжение UC на обкладках конденсатора и расстояние между ними. Так как конденсатор является проводником, то это напряжение не равно ЭДС подключенного источника; чтобы его найти, нужно знать сопротивление конденсатора. Если плоский конденсатор с площадью обкладок S и расстоянием между ними d заполнен проводящим диэлектриком с проницаемостью ε и удельным сопротивлением ρ, то емкость и сопротивление конденсатора равны соответственно: Завдання Умова: Плоский конденсатор ємністю С заповнений проводним діелектриком з проникністю ε і питомим опором ρ. Відстань між пластинами дорівнює d. Через резистор опором R конденсатор підключений до джерела з ЕРС Ɛ і внутрішнім опором r. Визначте напруженість електричного поля в діелектрику. Рішення:
Матеріали, які володіють зазвичай діелектриками, в тій чи іншій мірі володіють електропровідністю. Якщо до джерела постійного струму підключити конденсатор, заповнений проводним діелектриком, в ланцюзі піде електричний струм (струм витоку). Між пластинами конденсатора буде існувати електричне поле, напруженість якого Е можна визначити, знаючи напругу UC на обкладках конденсатора і відстань між ними. Так як конденсатор є провідником, то це напруження не дорівнює ЕРС підключеного джерела; щоб його знайти, потрібно знати опір конденсатора. Якщо плоский конденсатор з площею обкладок S і відстанню між ними d заповнений проводним діелектриком з проникністю ε і питомим опором ρ, то ємність і опір конденсатора рівні відповідно: profmeter.com.ua
при этом мгновенный зарядный ток:
Мгновенная величина разрядного тока
от рассматриваемого напряжения. При заряде конденсатора постоянная времени указывает время (в секундах), в течение которого напряжение на обкладках повышается на 63% от разницы между имевшимся напряжением и напряжением источника тока заряда.
В связи с тем что заряд и разряд до полных значений конечных напряжений длятся неопределенно долгий срок, часто удобнее считать режим заряда законченным при доведении напряжения на обкладках до 99% от заряжающего напряжения (или до 1% от первоначальной величины напряжения при разряде).
Для пользователей XMPP клиентов, используется команда
fiz ключи
где ключи это известные параметры, параметра=значение, разделенные точкой с запятой
Обязателен ключ key=razryad при расчете разаряда конденсатора
и zaryad при расчете заряда
Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.
Заметьте, чем данный калькулятор отличается от других:
Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)
Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.
Определим время заряда конденсатора ёмкостью 1микроФарад, до 5 Вольт, если сопротивление цепи 1 килоОм.
Напряжение внешнего источника питания 12 Вольт, а на обкладках конденсатора напряжение, в момент подключения источника питания, составляло 1 Вольт.
Что бы сразу хотелось бы заметить. Как видно из задачи у нас есть остаточное напряжение на конденсаторе в размере 1 Вольт, которое надо учитывать в расчетах времени заряда.
Данные, которые мы будем вводить следующие:
U0=12-1 =11В
Ut=5-1=4В
R=1кОм
С=1мкФ
пишем запрос fiz U0=11В;Ut=4В;R=1кОм;C=1мкФ;key=zaryad
и получаем ответ
U0 = 11 Вольт
Ut = 4 Вольт
R = 1 килоОм
C = 1 микрофарад
T = 1 милисекунда
tt = 0.4519851237 милисекунда
То есть решение = 451.98 мкс
Теперь давайте проверим наши расчеты. Если бы конденсатор был бы в момент подключения источника питания полностью разряжен
То при условии зарядки его до 1 Вольта наш запрос был бы таким
fiz U0=12В;Ut=1В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 87.011377 микросекунда
а при зарядки до 5 Вольт был бы таким
fiz U0=12В;Ut=5В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 538.9965007 микросекунда
То время заряда конденсатора с 1В до 5 Вольт составило бы 538.9965007 микросекунда минус 87.011377 микросекунда = 451.98 мкс
Что несомненно говорит о правильности наших расчетов по изначальным условиям.
5 3 51 www.abakbot.ru 9. Конденсатор faza-s.narod.ru
Соединение конденсаторов в электрической цепи может быть последовательным,
параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить,
что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:
Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ
при последовательном соединении резисторов.
Формула Cобщ при последовательном соединении конденсаторов = формула Rобщ при
параллельном соединении резисторов.
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами.
В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок,
равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо
пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме
емкостей всех конденсаторов в цепи.
Параллельное соединение конденсаторов
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит,
потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение).
Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
Падение напряжения при параллельном соединении
Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
При параллельном соединении через каждый конденсатор
потечет одельный ток, в зависимости от емкости конденсатора:
Ток при параллельном соединении
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов
в форме цепи, в которой каждый отдельный конденсатор соединяется с другим
отдельным конденсатором только в одной точке.
Последовательное соединение конденсаторов
Ток (iC), заряжающий последовательную цепь конденсаторов,
будет одинаковым для всех конденсаторов, поскольку у
него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток,
количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо
от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого
конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы
имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора
С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3.
Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора.
Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом,
данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи,
и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается
до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента
с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение.
Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость
конденсатора, тем большее напряжение на него упадет.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:
Падение напряжения при последовательном соединении
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна
его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные
конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.
Следовательно:
Разделив все выражение на Qобщ мы получим уравнение для
общей емкости при последовательном соединении:
Из данного уравнения можно легко вывести формулу общей емкости
для любого частного случая последовательного соединения.
Например, общая емкость для трех конденсаторов:
Общая емкость для двух конденсаторов:
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной
или последовательно-параллельной. Тем не менее, смешанное соединение может иметь
как последовательный, так и параллельный характер.
Смешанное соединение конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму,
как и при расчете общего сопротивления смешанного соединения резисторов.
Так это будет выглядеть для схемы 2: Преобразование смешанного соединения в параллельное
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы
последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит
в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью.
Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых,
обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги
на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов
еще есть хоть какая-то логика, то кому вообще нужно смешанное?
Дело в том, что емкостью, то есть способностью накапливать электрический заряд,
обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи,
то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы.
Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов,
которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат.
Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных
компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости,
прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки,
нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.
hightolow.ruПлоский конденсатор. Заряд и емкость конденсатора. Напряжение конденсатора формула
Плоский конденсатор. Заряд и емкость конденсатора.

Плоский конденсатор.
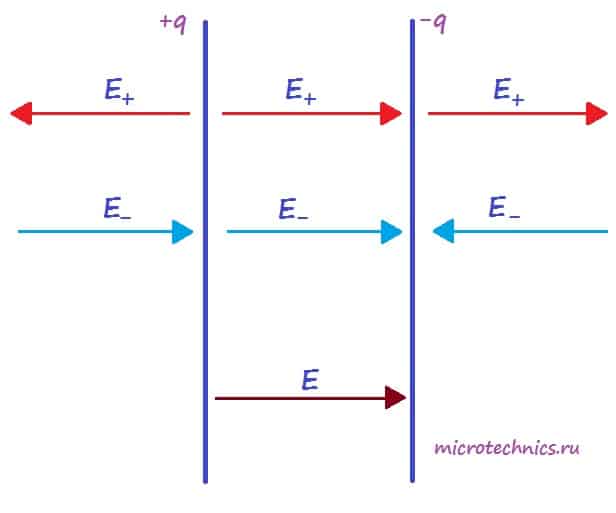
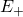

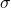 – это поверхностная плотность заряда:
– это поверхностная плотность заряда: 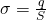 . А
. А  – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
– диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой: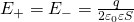
Процессы зарядки и разрядки конденсаторов.
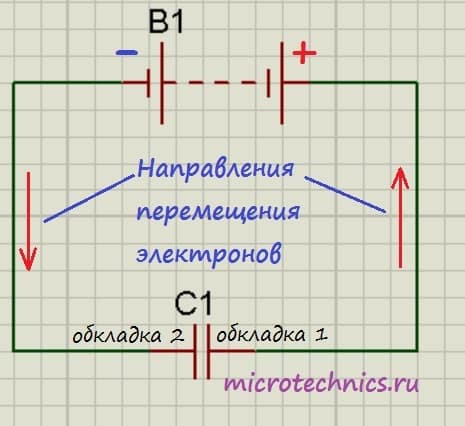 Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?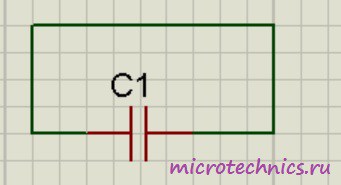 В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.Емкость и энергия конденсатора.
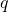 одного из проводников к разности потенциалов между проводниками:
одного из проводников к разности потенциалов между проводниками: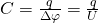
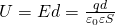
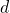 – это расстояние между пластинами конденсатора, а
– это расстояние между пластинами конденсатора, а 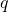 – заряд конденсатора. Подставим эту формулу в выражение для емкости конденсатора:
– заряд конденсатора. Подставим эту формулу в выражение для емкости конденсатора: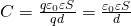
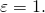
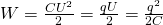
Напряженность электрического поля
Заряд и разряд конденсатора через сопротивление
Полученные характеристики ЗАРЯДА конденсатора через сопротивление  от источника тока через наружное сопротивление
от источника тока через наружное сопротивление  происходит в соответствии с формулой
происходит в соответствии с формулой 

 - рассматриваемый момент времени в секундах от момента начала заряда;
- рассматриваемый момент времени в секундах от момента начала заряда;  - напряжение на обкладках конденсатора момент времени t в Вольтах;
- напряжение на обкладках конденсатора момент времени t в Вольтах;  - напряжение источника, от которого производится заряд конденсатора в Вольтах
- напряжение источника, от которого производится заряд конденсатора в Вольтах 
 - емкость конденсатора в Фарадах
- емкость конденсатора в Фарадах  - сопротивление последовательной цепи в Омах
- сопротивление последовательной цепи в Омах 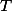 - постоянная времени в секундах (
- постоянная времени в секундах ( ).
).  , заряженного до разности потенциалов
, заряженного до разности потенциалов  через сопротивление
через сопротивление  представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой
представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой 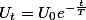

 - напряжение между обкладками конденсатора через
- напряжение между обкладками конденсатора через  секунд после начала разряда,
секунд после начала разряда, — ток в цепи (внешней или внутренней) конденсатора существующей через
— ток в цепи (внешней или внутренней) конденсатора существующей через  секунд после начала разряда.
секунд после начала разряда. Полученные характеристики РАЗРЯДА конденсатора через сопротивление  . Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в
. Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в  раз,
раз,
Синтаксис
Примеры использования бота
Заряд и разряд конденсатора через сопротивление | 2014-06-23 10:12:35 | Варламов Дмитрий | Электротехника онлайн |
Сборник формул для радиолюбителей
Последовательное и параллельное соединение конденсаторов
Параллельное соединение конденсаторов

Напряжение при параллельном соединении
Ток при параллельном соединении

Последовательное соединение конденсаторов
Ток при последовательном соединении


Падение напряжения и общая емкость при последовательном соединении

Смешанное соединение конденсаторов

Общая емкость смешанного соединения конденсаторов

Зачем все это нужно?
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''




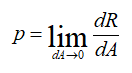





Поделиться с друзьями: