Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде). u = Umsin(2πt + Ψ ) = Umsin(ωt + Ψ ) Где u = u(t) — мгновенное значение переменного напряжения [В]. Um — максимальное значение напряжения (амплитудное значение) [В]. f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1) ω — угловая частота (омега) (единица угловой частоты — рад/с или с-1) ω = 2πf = 2π/T Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t. U — Действующее значение напряжения [В]: Рассмотрим параметры напряжения в бытовой электросети. Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.). Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения. electrikam.com Лекция №5 Переменным называется ток, изменение которого по величине и направлению повторяется периодически через равные промежутки времени Т. В области производства, передачи и распределения электрической энергии переменный ток имеет по сравнению с постоянным, два основных преимущества: 1) возможность (при помощи трансформаторов) просто и экономично повышать и понижать напряжение, это имеет решающее значение для передачи энергии на большие расстояния. 2) большую простоту устройств электродвигателей, а следовательно, и их меньшую стоимость. Значение переменной величины (тока, напряжения, ЭДС) в любой момент времени t называется мгновенным значением и обозначается строчными буквами (ток i, напряжение u, ЭДС – е). Наибольшее из мгновенных значений периодически изменяющихся токов, напряжений или ЭДС, называются максимальными или амплитудными значениями и обозначаются прописными буквами с индексом «м» (Iм, Uм). Наименьший промежуток времени, по прошествии которого мгновенные значения переменной величины (ток, напряжение, ЭДС) повторяется в той же последовательности, называется периодом Т, а совокупность изменений, происходящих в течение периода, - циклом. Величина обратная периоду называется частотой и обозначается буквой f. , т.е. частота – число периодов за 1 секунду. Единица частоты 1/сек – называется герц (Гц). Более крупные единицы частоты – килогерц (кГц) и мегагерц (МГц). Стандартная (техническая) 50 Гц Частота для промышленных установок Европе, Японии и Америки 60 Гц Переменные токи и напряжения в технике стремятся получить по простейшему периодическому закону – синусоидальному. Т. к. синусоида – единственная периодическая функция, имеющая подобную себе производную, в результате чего во всех звеньях электрической цепи форма кривых напряжений и токов получается одинаковой, чем значительно упрощаются расчеты. Для получения токов промышленной частоты служат генераторы переменного тока в основе работы которых лежит закон электромагнитной индукции, согласно которому при движении замкнутого контура в магнитном поле в нем возникает ток. Схема простейшего генератора переменного тока Генераторы переменного тока большой мощности, рассчитанные на напряжения 3 – 15 кв, выполняются с неподвижной обмоткой на статоре машины и вращающимся электромагнитом-ротором. При такой конструкции легче надежно изолировать провода неподвижной обмотки и проще отвести ток во внешнюю цепь. Одному обороту ротора двухполюсного генератора соответствует один период переменной ЭДС, наведенной на его обмотке. Если ротор делает n оборотов в минуту, то частота индуктированной ЭДС . Т.к. при этом угловая скорость генератора , то между ней и частотой, наведенной ЭДС существует соотношение. Фаза. Сдвиг фаз. Предположим, что генератор имеет на якоре два одинаковых витка, сдвинутых в пространстве. При вращении якоря в витках наводятся ЭДС одинаковой частоты и с одинаковыми амплитудами, т.к. витки вращаются с одинаковой скоростью в одном и том же магнитном поле. Но вследствие сдвига витков в пространстве ЭДС достигают амплитудных знамений неодновременно. Если в момент начала отсчета времени (t=0) виток 1 расположен относительно нейтральной плоскости под углом , а виток 2 под углом. То наведенная в первом витке ЭДС:, а во втором: В момент отсчета времени: Электрические углы иопределяющие значения ЭДС в начальный момент времени, называетсяначальными фазами. Разность начальных фаз двух синусоидальных величин одной частоты называется углом сдвига фаз. Та величина, у которой нулевые значения (после которых она принимает положительные значения), или положительные амплитудные значения достигаются раньше, чем у другой, считается опережающей по фазе, а та у которой те же значения достигаются позже – отстающей по фазе. Если две синусоидальные величины одновременно достигают своих амплитудных и нулевых значений, то говорят, что величины совпадают по фазе . Если угол сдвига фаз синусоидальных величин равен 1800, то говорят, что они изменяются впротивофазе. studfiles.net Переменный электрический ток, равно как переменное напряжение, изменяют свое направление и значение на протяжении определенного отрезка времени. Поскольку данный ресурс носит более прикладной, нежели теоретический характер, то здесь тема переменного электрического тока и напряжения будет рассмотрена в объеме, достаточном для понимания сути этих процессов и не более того. Изменение тока (напряжения) во времени могут иметь достаточно сложный характер, но всегда существует возможность представить их в виде совокупности ряда колебаний, изменяющихся по синусоидальному закону (рис.1). Те напряжения и ток, которыми мы пользуемся в повседневной жизни подчиняются этому же закону. Возьмем произвольную точку и начнем вращать ее по окружности с угловой скоростью ω (рисунок 1.а). При этом она последовательно пройдет все точки окружности, в том числе 1,2,3,4, после чего цикл повторится. Если все это спроецировать на оси Х (значение тока или напряжения) и t (время), то получим график, изображенный на рисунке 1 (там эти точки тоже обозначены), который поясняет суть переменного тока или напряжения. Время T=t4-t1 за которое происходит один цикл колебания называется периодом. Зависимость периода от частоты колебаний находится в обратно пропорциональной зависимости T=1/f, где f - частота колебаний (величина, характеризующаяся количеством колебаний в единицу времени). Единица измерения частоты - Герц (Гц). 1 Герц- это одно колебание в секунду. Частота колебаний в Российской сети переменного тока 50 Гц. (В некоторых странах частота тока составляет 60 Гц.). Теперь, собственно о том, зачем я приводил пример с вращением точки по окружности. Предположим, нужно определить относительное положение точки 1 от точки 2. Вроде напрашивается привязать их к оси t, тогда получим расстояние между ними Δt=t2-t1, но для разных частот эта величина будет различна. Если же учесть, что полный оборот всегда равен 3600 или 2π радиан, то всегда можно сказать, что точка 2 сдвинута относительно точки 1 на 900 (π/2). Кстати, это называется фазовым сдвигом и пригодится нам при рассмотрении трехфазного тока (или напряжения - как угодно). Пора перейти к рисунку 2. Все знают, что напряжение бытовой электрической сети переменное и должно быть 220 В. Так вот, если Вы думаете, что это значение можно присвоить точке А, то ошибаетесь. Судите сами, переменное напряжение то возрастает, то уменьшается, в какие то моменты оно вовсе равно нулю, но свою работу оно делает. Эта работа определяется площадью (желтый цвет), ограниченной синусоидой и осью t (нулевое значение). Если построить прямоугольник такой же площади (заштрихован), то его верхняя граница, находящаяся на отметке а (малое) будет соответствовать значению 220В. Это называется действующее значение напряжения. Амплитудное значение напряжения выше, взаимосвязь между ними определяется формулой A=a*√2, то есть максимальное значение напряжения в сети может достигать 311 В. Это справедливо для любых переменных напряжений, что следует учитывать, например, выбирая максимально допустимое обратное напряжение диода при включении его в цепь переменного тока. В заключение - немного про трехфазный ток. В промышленных масштабах у нас вырабатывается именно он. Генератор трехфазного тока имеет три катушки, расположенные под углом 1200 (рисунок 3). Соответственно, в каждой из них при вращении в магнитном поле наводится электрический ток. Токи катушек сдвинуты по фазе друг относительно друга на те же 1200. При подключении трехфазных потребителей энергии необходимо учитывать порядок подключения фаз. Последовательность подключения может иметь следующие варианты: Это обусловлено тем, что переменный трехфазный ток способен создавать вращающееся магнитное поле, при неправильном подключении направление его вращения будет меняться на противоположенное, что может повлечь нарушение работоспособности некоторых устройств. Стоит сказать, что бытовая однофазная электрическая сеть ни что иное как часть трехфазной цепи, использующая для работы нулевой (N) провод и одну из фаз A(L1), B(L2), C(L3). При подключении однофазных потребителей следует равномерно распределять нагрузку между всеми тремя фазами. Может возникнуть вопрос: почему трехфазная цепь имеет напряжение 380В, а однофазная 220В ? Дело в том, что напряжения между фазами UАВ, UАС, UВС составляют 380 Вольт, а между любой фазой и "нулем" UAN, UBN, UCN - 220 Вольт. Именно поэтому ошибочное подключение одной из фаз на нулевой провод может вывести из строя бытовую технику, рассчитанную на напряжение 220В. © 2012-2018 г. Все права защищены. Все представленные на этом сайте материалы имеют исключительно информационный характер и не могут быть использованы в качестве руководящих и нормативных документов eltechbook.ru data-ad-client="ca-pub-5076466341839286"data-ad-slot="1404500382">♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1. Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.Период измеряется в секундах и обозначается буквой Т.Количество периодов переменного тока за 1 секунду, есть частота f.Частота переменного тока f измеряется в герцах . f = 1 / T. Например.Частота в нашей электрической сети 50 Гц. Период этих колебаний будет равен: T = 1 / f = 1 / 50 = 0,02 сек. Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой. Umax = Ua и Imax = Ia За один период напряжение принимает эти значения два раза: + Ua и — Ua . ♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.Введено понятие действующего значения переменного напряжения Uд и тока Iд. Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток. ♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.Следовательно действующее (или эффективное) значение переменного тока будет равно: Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения На все эти теоретические размышления можно посмотреть иначе! ♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.После выпрямительных диодов оно принимает вид как на рисунке 2. Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования. ♦На рисунке приняты обозначения: Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу. Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.♦Проведем линию, обозначающую Uд = 0,707.Она отсекает верхнюю часть половинок синусоид.Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.Одна и та же электрическая мощность, выраженная в трех видах. P = Ua х Ia = Uд х Iд = U х I ♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.Максимальное, амплитудное значение напряжения в сети равно:Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт. Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей. data-ad-client="ca-pub-5076466341839286"data-ad-slot="1404500382"> domasniyelektromaster.ru Ток, изменяющийся во времени по значению и направлению, называется переменным. В практике применяют периодически изменяющийся по синусоидальному закону переменный ток (рис.10). Синусоидальные величины характеризуются следующими основными параметрами: периодом, частотой, амплитудой, начальной фазой или сдвигом фаз. Период Т — время (с), в течение которого переменная величина совершает полное колебание. Частота f — число периодов в секунду. Единица измерения частоты — герц (сокращенно Гц). 1 Гц равен одному колебанию в секунду. Период и частота связаны зависимостью Т=I/f. Промышленный переменный ток имеет частоту 50 Гц. Можно представить, что полярность зажимов источника переменного тока с частотой 50 Гц меняется 100 раз в секунду. Изменяясь с течением времени, синусоидальная величина (напряжение, ток, э.д.с) принимает различные значения. Значение величины в данный момент времени называют мгновенным. Амплитуда — наибольшее значение синусоидальной величины. Амплитуды тока, напряжения и э.д.с. обозначают прописными буквами с индексом: Iм, Um, Ем, а их мгновенные значения — строчными буквами i, u, е. Мгновенное значение синусоидальной величины, например, тока определяют по формуле : где ωt+Ψ -фаза-угол, определяющий значение синусоидальной величины в данный момент времени; Ψ- начальная фаза, т.е. угол, определяющий значение величины в данный момент времени. Если синусоидальные величины имеют одинаковую частоту, но разные начальные фазы, то в этом случае говорят, что они сдвинуты по фазе. Разница начальных фаз определяет угол сдвига фаз. На рис. 11 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны, то разница равна 0, значит сдвига фаз нет (рис.12). Эффективность механического и теплового действия переменного тока оценивается действующим его значением. Действующее значение переменного тока равно такому значению постоянного тока, который за время, равное одному периоду переменного тока, выделит в том же сопротивлении такое же количество тепла, что и переменный ток. Действующее значение обозначают прописными буквами без индекса: I, U, E. Для синусоидальных величин действующие и амплитудные значения связаны соотношениями : Амперметры и вольтметры переменного тока измеряют действующие значения тока и напряжения, а ваттметры — среднее значение мощности. В цепи переменного тока, состоящей из резистора R, напряжение и ток совпадают по фазе u=UM sin ωt. На рис. 13 приведена векторная диаграмма тока и напряжения для цепи с резистором. Средняя за период мощность цепи с резистором называется активной мощностью; равна она произведению действующих значений напряжения и тока: P—UI. Изменение тока в цепи с индуктивностью L вызывает э.д.с. самоиндукции, которая по закону Ленца противодействует изменению тока. При увеличении тока э.д.с. самоиндукции действует навстречу току, а при убывании — в направлении тока, противодействуя его уменьшению. Вследствие этого ток в цепи с катушкой индуктивности отстает от напряжения на угол π/2 радиан (рис.14) (четверть периода). Закон Ома для цепи переменного тока, содержащей индуктивность будет иметь вид Величина xL называется индуктивным сопротивлением цепи или реактивным сопротивлением индуктивности, измеряется в омах. При включении в цепь переменного тока конденсатора (рис.15,а) происходит непрерывное перемещение электрических зарядов. При увеличении напряжения ток в цепи конденсатора будет зарядным, а при уменьшении — разрядным. Поэтому ток в цепи, содержащий конденсатор, опережает напряжение на угол π/2 радиан (рис.15,б). На векторной диаграмме (рис.15,в) вектор тока Iс опережает вектор приложенного напряжения U. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид I= Uc/xc Величина хс называется емкостным сопротивлением или реактивным сопротивлением емкости, которую определяют по формуле: При последовательном соединении катушки индуктивности и конденсатора их реактивные сопротивления вычитаются, т. е. х = xL - xС. Эта величина называется реактивным сопротивлением цепи. Геометрическая сумма активного и реактивного сопротивлений равна полному сопротивлению электрической цепи, т. е. R2 + x2= R2+(xL-xc)2 = Z2. Эта зависимость показывает, что, используя значения R, х и z, можно построить треугольник сопротивлений (рис.16). Умножая значение сторон этого треугольника на силу тока в цепи, получим треугольник напряжений. Умножив сопротивления на квадрат тока, получим треугольник мощностей. Работающие электрические установки потребляют активную и реактивную мощности и энергию. Лампы накаливания и электрические нагревательные приборы потребляют практически только активную мощность. Такие же электроприемники, как асинхронные электродвигатели, трансформаторы, дроссели, линии электропередачи и др., потребляют и активную, и реактивную мощности. Потребность электроустановок в активной и реактивной мощностях покрывается энергией, вырабатываемой генераторами электростанций. Активная энергия преобразуется потребителями в другие виды энергии: тепловую, световую, механическую и др. Потребляемая предприятиями реактивная мощность есть мощность, идущая на создание переменного магнитного потока (магнитного поля). Магнитный поток, сцепляющийся с контуром электрической цепи, пропорционален току в этой цепи. Мерой пропорциональности служит так называемая индуктивность цепи, предопределяющая в каждом конкретном случае числовую связь между током и магнитным потоком. Следовательно, с любой цепью переменного тока, в которой и напряжение и ток изменяются по периодической кривой, сцепляется переменный (периодически изменяющийся) магнитный поток. Как известно, магнитный поток ведет себя таким образом, что ему можно приписать некоторого рода инерцию. Поэтому при всяком приращении (или уменьшении) магнитного потока, вызванном увеличением (или уменьшением) силы тока, неизбежно должно проявляться своего рода инерциальное сопротивление магнитного потока. Это сопротивление проявляется в форме э.д.с. самоиндукции, представляющей собой электромагнитную реакцию всегда обратного знака по отношению к изменению магнитного потока. Это означает, что э.д.с. самоиндукции всегда стремится изменить силу тока таким образом, чтобы ослабить или замедлить изменение магнитного потока, сцепляющегося с контуром. Отсюда следует, что переменное напряжение источника электрической энергии должно содержать кроме составляющей, расходуемой на тепловые процессы, обусловленные наличием активного сопротивления, еще и такую составляющую, которая в каждый момент времени компенсировала бы э.д.с. самоиндукции. Следовательно, мгновенное значение мощности в цепи переменного тока также должно в любой момент времени представлять собой сумму двух слагаемых: активной мощности, расходуемой в активных сопротивлениях, и реактивной мощности, вызванной действием э.д.с. самоиндукции. В течение первой четверти каждого периода, когда ток увеличивается от нуля до наибольшего значения, соответственно растет (в результате преодоления э.д.с. самоиндукции) и магнитный поток. При этом в магнитном поле имеет место накопление энергии за счет реактивной мощности, поступающей из генератора в цепь потребителя. В течение второй четверти каждого периода, когда ток и магнитный поток уменьшаются (от наибольшего значения до нуля), энергия магнитного поля также уменьшается до нуля. Это уменьшение энергии магнитного поля сопровождается возвращением реактивной мощности из цепи потребителя в генератор (под действием обратно направленной э.д.с. самоиндукции). Таким образом, мощность, идущая на создание магнитного поля, четыре раза в течение каждого периода меняет свое направление, причем среднее значение этой мощности за каждый полупериод (или целое число полупериодов) равно нулю, так как процесс обмена мощностью между генератором и цепью потребителя происходит в форме колебательного процесса. Отношение активной мощности (Р) к полной мощности (5) электроустановки называется коэффициентом мощности: где S,P и Q - соответственно полна, активная и реактивная мощности. Полную мощность определяют по формуле S=UI. Измеряется полная мощность в вольт-амперах (В•А). Активную мощность определяют по формуле P=UIcosφ. Измеряется активная мощность в ваттах (Вт). Реактивную мощность определяют по формуле Q=UIsinφ. Измеряется активная мощность в вольт-амперах реактивных (вар). В процессе эксплуатации электроустановок коэффициент мощности изменяется с изменением величины и характера нагрузки. Коэффициент мощности определяют по показаниям счетчиков активной и реактивной энергии за определенный промежуток времени (сутки, месяц, год) по формуле , где Wa- разность показаний счетчитка активной энергии; Wp - разность показаний счетчика реактивной энергии. При этом получают коэффициент мощности, который называется средневзвешенным, т. е. средним. При низком коэффициенте мощности увеличиваются потери энергии в проводах, а при сохранении потерь неизменными требуется применение проводов увеличенного сечения. Таким образом, коэффициент мощности является показателем эффективности использования электрической энергии. Обмотки трехфазных электродвигателей, применяемых в сельскохозяйственном производстве, обладают активным и индуктивным сопротивлением. Основными мероприятиями для повышения коэффициента мощности, а следовательно, и экономии электроэнергии являются следующие: incub.info Электрический ток бывает постоянным и переменным. Переменный – это ток, в котором среднее значение за период силы и напряжения равно нулю. Такой ток непрерывно изменяется по величине и направлению, и происходят эти изменения через равные промежутки времени. Периодический переменный ток. Известно, что, для того чтобы вызвать в цепи переменный ток, используют генераторы переменного тока. В таких генераторах электродвижущая сила (ЭДС) возникает в процессе электромагнитной индукции. В полости цилиндрической формы вращается магнит, называемый ротором, а неподвижный сердечник с его обмоткой называется статором. Переменный ток применяется в устройствах связи (радио, телевидение, проволочная телефония и пр.), и все это благодаря тому, что напряжение и силу переменного тока можно преобразовывать почти без потери энергии. Для промышленности и освещения переменный ток вырабатывается генераторами, приводимыми во вращение водяными или паровыми турбинами и двигателями внутреннего сгорания. Переменный ток бывает однофазным и многофазным. Из многофазных широкое распространение получил трехфазный ток - система переменного тока, состоящая из трех электрических цепей, имеющих одинаковую частоту и электродвижущую силу, сдвинутые по фазе на 120°. Трехфазная система переменного тока применяется в промышленности для питания электродвигателей, электропечей, освещения. Схема простейшего генератора переменного тока. При прохождении по проводнику переменный ток выделяет столько же тепла, сколько и постоянный. Время, в течение которого совершается одно колебание, называют периодом (обозначают буквой Т). Состояние переменного тока в отдельные моменты времени называют фазами. А число периодов в секунду – частотой. Единицей частоты является герц (Гц). Если мы говорим, что в одну секунду совершается одно колебание, то частота будет равна 1 Гц. При помощи выпрямителей переменный ток может быть преобразован в постоянный (для большинства устройств требуется постоянный ток). Долгое время в электротехнике применялся исключительно постоянный ток. Но потом возникла необходимость в передаче электроэнергии на дальние расстояния. В быту обычно используется переменный ток, поэтому мы расскажем подробнее о нем и его физических характеристиках. При передаче электроэнергии по проводам в них возникают потери, пропорциональные квадрату тока. Для уменьшения потерь необходимо уменьшить ток. Но для передачи той же мощности при меньшем токе необходимо более высокое напряжение. Поэтому передача электроэнергии на дальние расстояния может быть выполнена только при высоком напряжении. Преобразование с малыми потерями больших токов низкого напряжения в малые токи высокого напряжения, или наоборот, может производиться лишь посредством электромагнитного аппарата переменного тока — трансформатора. Поэтому в настоящее время преимущественно применяется переменный электрический ток. Ток, изменяющийся в течение определенного времени по величине и направлению, называется переменным током. Переменный ток, изменяющийся по синусоидальному закону, представляет собой однофазный синусоидальный ток:i = IM sin (wt + cp),где IM — амплитудное значение тока. Промежуток времени, в течение которого осуществляется одно полное колебание, называется периодом Т. Число периодов в секунду называется частотой, которая выражается формулойF = 1/ТЧастота измеряется в герцах (Гц). Величина w = 2яср = 2л/Т называется угловой частотой и измеряется в рад/сек; угол Zwcp называется начальной фазой. На практике наибольшее распространение получил ток, который изменяется с частотой 50 периодов в секунду, т. е. 50 Гц. Поделитесь полезной статьей: fazaa.ru Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток. Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток. Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника или Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону. Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону: где u – мгновенное значение напряжения, Um – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения. Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц. Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е. Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением. Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1). Рис. 1 Пусть напряжение на концах цепи меняется по гармоническому закону Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома: Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление: Рис. 2 При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока. Индуктивность влияет на силу переменного тока в цепи. Это можно обнаружить с помощью простого опыта. Составим цепь из катушки большой индуктивности и лампы накаливания (рис. 3). С помощью переключателя можно присоединять эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть одинаковы. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока. Рис. 3 Объясняется это самоиндукцией. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех установившихся значений, которые она приобрела бы с течением времени при постоянном напряжении, равном максимальному значению переменного напряжения. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью L цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. Докажем это математически. Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4). При изменениях силы тока по гармоническому закону в катушке возникает ЭДС самоиндукции где L – индуктивность катушки, ω – циклическая частота переменного тока. Рис. 4 Так как электрическое сопротивление катушки равно нулю, то ЭДС самоиндукции в ней в любой момент времени равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором: Следовательно, при изменении силы тока в катушке по гармоническому закону напряжение на ее концах изменяется тоже по гармоническому закону, но со сдвигом фазы: Следовательно, колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (рис. 5). В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Рис. 5 Произведение \(I_m \cdot L \cdot \omega\) является амплитудой колебаний напряжения на катушке: Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний силы тока в ней называется индуктивным сопротивлением (обозначается XL): Связь амплитуды колебаний напряжения на концах катушки с амплитудой колебаний силы тока в ней совпадает по форме с выражением закона Ома для участка цепи постоянного тока: В отличие от электрического сопротивления проводника в цепи посто-янного тока, индуктивное сопротивление не является постоянной величиной, характеризующей данную катушку. Оно прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю (XL = 0). Зависимость амплитуды колебаний силы тока в катушке от частоты приложенного напряжения можно наблюдать в опыте с генератором пере-менного напряжения, частоту которого можно изменять. Опыт показывает, что увеличение в два раза частоты переменного напряжения приводит к уменьшению в два раза амплитуды колебаний силы тока через катушку. Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы. При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения. Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы. Рис. 6 Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону заряд на его обкладках изменяется по закону: Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону: Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д. Рис. 7 Произведение \(U_m \cdot \omega \cdot C\) является амплитудой колебаний силы тока: Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC): Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора: Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте. Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой ω и амплитудой Um, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im. Установим связь между амплитудами колебаний силы тока и напряжения. Рис. 8 В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения: Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону: Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на π/2. Поэтому уравнение (1) можно записать так: где URm, UCm и ULm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке. Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм. При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения URm, совпадает по направлению с вектором, изображающим амплитуду силы тока Im. Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор \(~\vec U_{Cm}\) отстает от вектора \(~\vec I_{m}\) на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор \(~\vec U_{Lm}\) опережает вектор \(~\vec I_{m}\) на угол 90° (рис. 9). Рис. 9 На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) , вращающихся с одинаковой угловой скоростью ω против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений uR, uC и uL на отдельных элементах цепи, т. е. сумме проекций векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов: Из рисунка 9 видно, что амплитуда напряжений на всей цепи равна или Отсюда Введя обозначение для полного сопротивления цепи переменного тока выразим связь между амплитудными значениями силы тока и напряжения в цепи переменного тока следующим образом: Это выражение называют законом Ома для цепи переменного тока. Из векторной диаграммы, приведенной на рисунке 9, видно, что фаза колебаний полного напряжения равна ω∙t + φ. Поэтому мгновенное значение полного напряжения определяется формулой: Начальную фазу φ можно найти из векторной диаграммы: Величина cos φ играет важную роль при вычислении мощности в электрической цепи переменного тока. Мощность в цепи постоянного тока определяется произведением напряжения на силу тока: Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой: Пусть напряжение на концах цепи меняется по гармоническому закону (с тем же успехом, разумеется, вместо \(~u = U_m \cdot \cos \omega t\) можно было бы записать \(~u = U_m \cdot \sin \omega t\)), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения: где φc – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать: При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период. Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов: В рассматриваемом случае α = ω∙t и β = ω∙t + φc. Поэтому Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени: При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно: Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I2∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим Действующим значением силы тока называют величину, в \(~\sqrt{2}\) раз меньшую ее амплитудного значения: Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока. Аналогично можно доказать, что действующее значение переменного напряжения в \(~\sqrt{2}\) раз меньше его амплитудного значения: Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать: Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле называется коэффициентом мощности. В случае, когда φc = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φc = - π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть. Рис. 10 Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит. При проектировании цепей переменного тока нужно добиваться, чтобы cos φc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов. Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85. www.physbook.ruНапряжение цепи переменного тока. Напряжение переменного тока
Напряжение цепи переменного тока | Электрикам
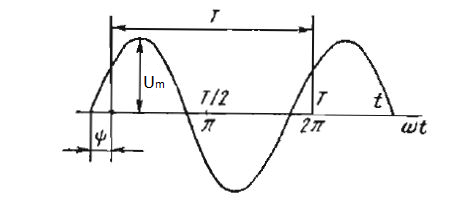

Переменный электрический ток.
Получение переменного синусоидального тока.
Переменный ток, трехфазные ток и напряжение

ТРЕХФАЗНЫЙ ТОК

синусоидальное переменное напряжение ток | Электрознайка. Домашний Электромастер.
Действующее значение синусоидальногопеременного напряжения – тока.


Переменный ток
Понятие о переменном токе


Referat. Переменный ток — PhysBook
Переменный ток
Резистор в цепи переменного тока
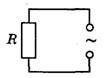
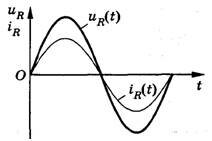
Катушка в цепи переменного тока
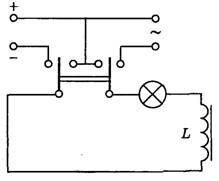
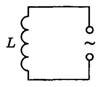
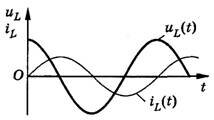
Конденсатор в цепи переменного тока


Закон Ома для электрической цепи переменного тока
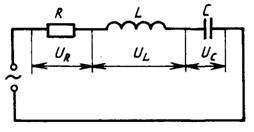
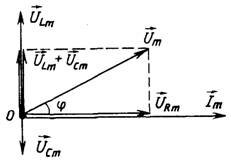
Мощность в цепи переменного тока

Литература
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''










Поделиться с друзьями: