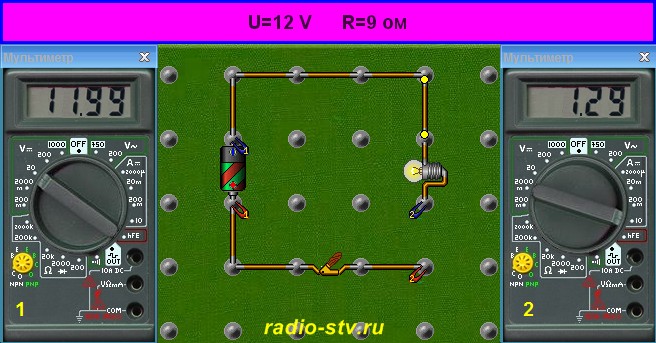
Доброго дня уважаемые радиолюбители!Приветствую вас на сайте “Радиолюбитель“ Единицы измерения служат для количественного определения какой-либо физической величины. К примеру, покупая яблоки, вы измеряете их вес в килограммах. Аналогично мультиметр измеряет сопротивление элементов в омах, напряжение — в вольтах, а ток — в амперах. В табл. 1.1 показаны общепринятые единицы измерения и их аббревиатуры для физических величин, которые используются в электронике. Таблица 1.1. Единицы измерения, используемые в электронике Переход к большим или меньшим величинам. При измерении веса яблок очень даже можно столкнуться с малым количеством яблока (или его кусочка), а можно измерять и центнерами, не так ли? Диапазон измерения физических величин в электронике еще шире. В одной схеме вы можете иметь сопротивление в миллионы ом, тогда как в другой протекающий ток будет меньше одной тысячной ампера. Говоря о подобных величинах — как громадных, так и предельно малых, — приходится иметь дело со специальной терминологией. Чтобы показывать очень большие и очень малые числа, в электронике применяют специальные префиксы, или приставки, и экспоненциальное представление. В табл. 1.2 показаны самые широко используемые префиксы и тип записи числовых величин. Тблица 1.2. Приставки, используемые в электронике Как же правильно прочитать число, записанное как 106 или 10-6? Экспоненциальное представление представляет собой наиболее удобный способ указания того, сколько нулей нужно добавить к числу в десятичной системе счисления, т.е. основанной на степени числа 10. Например, верхний индекс “6” в записи 106 означает, что точка, разделяющая целую и дробную части числа, должна находиться на шесть разрядов правее, а в записи 10-6 — что эту точку нужно сдвинуть на шесть разрядов левее. Таким образом, в числе 1 х 106 разделитель разрядов сдвигается на шесть мест вправо, и мы получаем в результате число 1 000 000 (1 миллион). В числе же 1 х 10-6 разделитель разрядов сдвигается на столько же мест влево, и результатом является 0,000001, или одна миллионная. 3,21 х 104 можно записать, сдвинув запятую на 4 знака вправо: 32100. Префиксы + единицы измерения = ? В предыдущих абзацах вы увидели как для обозначения физических величин и единиц их измерения используются аббревиатуры. В этом разделе мы научимся объединять их и использовать очень краткую запись. Например, ток 5 миллиампер можно записать в виде 5 мА, а частоту 3 мегагерца — как 3 МГц. Кроме того, так же, как при измерении яблок удобнее всего пользоваться килограммами, а при строительстве загородного офиса большой компании вес стальных конструкций определенно будут измерять не иначе как в тоннах, в электронике тоже существуют такие физические величины, для измерения которых пользуются большими числами, и такие, которые измеряются малыми. Это значит, что чаще всего вам придется иметь дело с одним и тем же набором приставок для каждой физической величины. Ниже приведены такие комбинации величин и единиц их измерения. > Ток: пА, нА, мкА, мА, А. > Индуктивность: нГн, мГн, мкГн, Гн. > Емкость: пФ, нФ, мкФ, мФ, Ф. > Напряжение: мкВ, мВ, В, кВ. > Сопротивление: Ом, кОм, МОм. > Частота: Гц, кГц, МГц, ГГц. Использование некоторых новых терминов Хотя ранее мы уже рассматривали такие понятия, как сопротивление, напряжение и ток, есть еще некоторые термины, которые могут оказаться для вас внове. Емкость представляет собой способность накапливать заряд под воздействием электрического поля. Такой накопленный заряд может повышать или понижать напряжение более плавно, чем в отсутствие емкости. Для применения данного свойства на практике используется такой компонент, как конденсатор. Частотой переменного тока называется мера повторяемости сигнала. Например, напряжение в настенной розетке совершает один полный цикл изменения 50 раз в секунду. Индуктивность – это способность запасать энергию в магнитном поле; эта накопленная энергия препятствует изменению тока точно так же, как энергия, накопленная конденсатором, препятствует резким изменениям напряжения. Для использования данного свойства на практике в электронике применяются катушки индуктивности, или дроссели. Мощность служит мерой количества работы, которую электрический ток совершает при протекании через элементы схемы. К примеру, если приложить к электрической лампе напряжение, подведя ток при помощи проводов, то на нагрев этих проводов будет затрачивться какая-то работа. В данном случае мощность можно вычислить, перемножив приложенное к лампе напряжение на ток, протекающий по проводам. Используя информацию, приведенную в табл. 1.1 и 1.2, вы уже можете перевести экспоненциальную запись числа или аббревиатуру физической величины на человеческий язык. Ниже дано несколько примеров: > мА: миллиампер, или 1 тысячная ампера; > мкВ: микровольт, или 1 миллионная вольта; > нФ: нанофарада, или 1 миллиардная фарады; > кВ: киловольт, или 1 тысяча вольт; > МОм: мегаом, или 1 миллион ом; > ГГц: гигагерц, или 1 миллиард герц. В аббревиатурах префиксов, которые представляют числа, превышающие 1, такие как М (для приставки Мега), используют прописные буквы. Аббревиатуры приставок, которые меньше 1, пишутся со строчной буквы — как, например, в слове милли. Единственным исключением из этого правила является приставка к для обозначения префикса кило-, которая также записывается с маленькой буквы. Иногда все же для обозначения тысяч используют и прописную литеру К — а именно при записи килоом; если вы увидите запись вида 3,3 К, то это будет значить 3,3 килоома. Вы должны научиться преобразовывать любое число к экспоненциальному виду, чтобы затем нормально проводить расчеты. Убедиться в этом вы сможете уже в следующем разделе. Понятие о законе Ома Итак, давайте предположим, что вы собрали свою первую схему. Вы знаете величину тока, которую компонент схемы может выдержать, не выходя из строя, и напряжение, выдаваемое источником питания. Следовательно, вам нужно рассчитать сопротивление, которое не позволит току в цепи превысить пороговое значение. В начале 1800-х годов Георг Ом опубликовал уравнение, названное впоследствии законом Ома, которое позволяет выполнить такой расчет. Закон Ома гласит: напряжение равняется произведению тока на сопротивление, или (в стандартной математической записи): U = I x R Помните ли вы из школы основы алгебры? Давайте еще раз вспомним вместе: если в уравнении с тремя величинами известны две, то достаточно легко рассчитать третью неизвестную величину. Закон Ома основывается именно на таком уравнении; члены уравнения можно переставлять как угодно, но зная любые два, всегда можно вычислить третий. Например, можно сказать, что ток является частным от деления напряжения на сопротивление: I = U / R Наконец, можно рассчитать сопротивление при известных токе и напряжении, переставив члены того же уравнения: R = U / I Итак, пока вроде бы все ясно. Теперь давайте попробуем проверить наши знания на практике: пусть есть схема, питающаяся от 12-вольтовой батареи, и электрическая лампа (скажем, большой фонарик). Перед установкой лампочки в фонарик вы измерили сопротивление схемы мультиметром и нашли, что оно равно 9 Ом. Вот формула для расчета электрического тока по закону Ома: I = U / R = 12 вольт / 9 Ом = 1,3 A Ну, а что, если вы обнаружили, что лампочка светит чересчур уж ярко? Яркость можно изменить, уменьшив ток, т.е. просто добавив в схему резистор. Изначально мы имели сопротивление схемы 9 Ом; добавив 5-омный резистор в схему, мы повысим ее сопротивление до 14 Ом. В этом случае ток будет равен: I = U / R = 12 вольт / 14 Ом = 0,9 А Предположим, что у вас есть схема с небольшой сиреной, которая имеет сопротивление 2 килоома, а также 12-вольтовая батарея. Для того чтобы рассчитать ток, вам нужно выразить сопротивление цепи не в килоомах, а в базовых единицах — омах, не используя приставку “кило”. В нашем случае это значит, что нужно разделить напряжение на 2000 Ом: I = U / R = 12 вольт / 2000 Ом = 0,006 A В результате мы получили ток, записанный как доля 1 А. После окончания расчета будет удобнее вновь использовать префикс, чтобы дать ответ в более лаконичном виде: 0,006 А = 6 мА Подводя итоги, можно сказать: для проведения расчетов необходимо все исходные величины преобразовать к базовым единицам счисления. Георг Ом (вот уж поистине, наш пострел везде поспел!) также нашел выражение для мощности, вычисляемое при известных напряжении и токе: Р = U х I; или Мощность = напряжение умноженное на силу тока. Это уравнение можно использовать для расчета мощности, потребляемой сиреной из предыдущего примера: Р = 12 В х 0,006 А = 0,072 Вт, или 72 мВт. Ладно, а что же делать, если напряжение на сирене нам не известно? Вы можете заняться простейшим преобразованием формулы для мощности, используя школьные знания (а вы-то думали, что зря протираете штаны на уроках физики!). Поскольку U = I х R, можно подставить это выражение в формулу для мощности, получив Р = I2 х R; или Мощность = сила тока в квадрате умноженная на сопротивление. Вы также можете использовать алгебраические преобразования, чтобы самостоятельно прикинуть, как можно рассчитать сопротивление, напряжение или ток, зная мощность и любой другой из этих же параметров. radio-stv.ru Всем привет, дамы и господа! Сегодня наконец речь пойдет о законе Ома. Да-да, это то, без знания чего вас заклюют на любом радиолюбительском форуме или паблике сотни уважаемых господ, которые в теме, пусть и не всегда действительно глубоко. Да что там паблики! Если ты, мой юный друг, посещаешь школу, лицей, гимназию или другое, без сомнения превосходное, учебное заведение, неправильный ответ на этот вопрос может привести в ярость почтенного преподавателя физики и закончиться для тебя не самым лучшим образом. Сегодняшний урок статья (мы же не в школе, в самом деле) направлена на предотвращения такого нехорошего сценария развития событий путем приобщения к еще одной очень важной (на самом деле так) тайне радиоэлектроники. Закон Ома на самом деле весьма прост. На великом и ужасном языке математики он выглядит следующим образом: В этой формуле I – уже известный нами ток, U – напряжение, R – cопротивление. Как вы видите, все величины мы рассмотрели ранее, они нам уже известны. В этой же статье мы рассмотрим, как они связаны между собой. Более того, мы уже видели раньше эту формулу в статье про сопротивлениe, правда тогда мы договорились, что не будем пока забегать вперед. Видите, зависимость совсем проста. Дифференциалов и страшных интегралов тут нет, а делить, вроде как вы, надуюсь, умеете. Так что на самом деле все несложно. Сила тока I в проводнике c сопротивлением R, оказывается, прямо пропорциональна приложенному к проводнику напряжению U и обратно пропорциональна сопротивлению проводника. Резонный вопрос – а откуда, собственно, эта связь взялась и сфига я должен ей верить? Если вы его задали – поздравляю, господа, вы на правильном пути. Действительно, с какой это стати верить всему написанному на слово? Та или иная зависимость может родиться двумя способами: результаты эксперимента или математический вывод формулок. Ну, здесь настолько простая формулка, что ответ один – эта зависимость получена экспериментальным путем уважаемым господином Георгом Омом. Грубо говоря, он взял источник напряжения (были в те времена так называемые «вольтовые столбы», кому интересно - гуглите) и куски металлической проволоки. Изменяя число вольтовых столбов (т.е. изменяя напряжение источника) или количество отрезков проволоки (т.е. изменяя сопротивление нагрузки), Ом получил данную зависимость. В тонкости физики измерений тех лет мы вникать не будем, это тема отдельной статьи. Кому интересно – гугл в помощь. Кто по-прежнему не верит – эксперимент в помощь. Вы всегда можете взять источник питания, который выдает точно известное напряжение, можете купить в магазине резистор с точно известным сопротивлением и мультиметром в режиме амперметра измерить протекающий в цепи ток. Дальше остается результат этого измерения сравнить с расчетным значением тока в цепи по приведенной формуле. Если вы все сделали правильно, результат эксперимента должен совпасть с расчетным значением. Схемка, иллюстрирующая этот эксперимент, приведена на рисунке 1. Рисунок 1 – Иллюстрация закона Ома Математика – математикой, а настоящего инженера должна интересовать в первую очередь физика процесса. К сожалению, есть люди даже среди почтеннейшей касты преподавателей, которые не уделяют должного внимания физике происходящего процесса, ограничиваясь лишь написанием формул, часто вообще без понимания сути происходящего. Если вы относите себя к их числу и вас устраивает данное положение дел, вероятно, есть смысл сейчас же безотлагательно покинуть данный ресурс. Невыполнение данного требования может повлечь существенные изменения в вашей психике! Автор не несет за это никакой ответственности! Итак, физика процесса. Возьмем источник напряжения. Разумеется, не ортодоксальные вольтовые столбы, а, например, лабораторный источник питания. Возьмем нагрузку. Например, обычный резистор 1,2 кОм. Выставим на источнике питания напряжение 12 В. Внимание, вопрос, господа знатоки. Какой будет протекать ток через резистор? Используя написанную нами выше формулку, получаем величину тока Т. е. ток через резистор равен 0,1 А или 100 мА. Допустим, мы хотим увеличить протекающий ток. Как это можно сделать? Очевидно, двумя способами – поднять напряжение источника питания или уменьшить сопротивление нагрузки-резистора. А если уменьшить протекающий ток? Аналогично – уменьшаем напряжение. Или увеличиваем сопротивление. Важно понимать, господа, что напряжение и сопротивление – это первичные величины. Они задаются конкретными девайсами – источником питания и резистором-нагрузкой. Они... как там это говорят... самобытны и самодостаточны. Они существуют сами по себе и, собственно, отлично живут без какого-то там тока. Сопротивление резистора ни в коем случае не зависит от источника напряжения! Оно ни в коем случае не зависит от протекающего тока! Оно может зависеть от материала резистора, от температуры, от формы, еще от чего-нибудь, но никак не от напряжения и тока (слышу вой уважаемый зануд, что это не так для нелинейных элементов – тссс! Спокойно, господа, до них тоже доберемся). От чего именно оно зависит, мы уже рассматривали здесь. Напряжение источника питания тоже тут величина первичная. Она определяется и формируется источником питания. А именно – переизбытком электронов на одном из электродов. Ток же здесь – вторичная величина, т.е. расчетная. Он существо подневольное, можно сказать, раб системы. Он зависит от напряжения и сопротивления. Сдохнет источник питания – каюк и току, он пропадет. Прикажет долго жить резистор, устав постоянно сопротивляться – на токе, несомненно, это тоже отразится (уменьшится или увеличится – отдельный вопрос, который решать будет все тот же уже почерневший резистор). Это рабство просто отлично характеризует картинка, которую мы любезно позаимствуем с pikaby Даже по выражению лиц на картинке отлично видно, кто тут подневольное существо, а кто командует парадом Читатель может возразить: "А как же источники тока?" Да, действительно есть такое понятие как "источник тока". Дескать, это такой девайс, у которого не напряжение первичная величина, а ток. То есть в теории он выдает через любое сопротивление строго один и тот же ток. Однако на практике возможности этих источников тока весьма ограничены. Как правило, они могут работать лишь при очень небольших нагрузочных сопротивлениях. Более того, если углубиться в физику процессов этих источников, то окажется, что там тоже идет игра за счет изменения напряжения. Поэтому-таки будем полагать, что первичной величиной является именно напряжение, а не ток. А про источники тока и источники напряжения потом поговорим более подробно. В инженерной практике, равно как и в школьных задачах, возникает задача следующего рода. Мы намерили ток, например, величиной в 1 А через известный резистор с сопротивлением, скажем, 10 Ом. Вопрос задачи: определите напряжение источника питания. Решается подобная задача весьма просто на основе того же закона Ома. Просто выражаем из уже написанной формулы напряжение: Абсолютно аналогичным образом можно посчитать и сопротивление, если мы знаем напряжение и ток. Итак, у нас теперь есть отличный инструмент, который связывает между собой напряжение, ток и сопротивление. Зная две из этих величины мы всегда сможем найти третью. Поверьте, на практике это встречается сплошь и рядом и это реально надо очень хорошо запомнить и понимать. Ну что ж, господа, на этом, думаю, сегодня можно закругляться. Поскольку тема и правда очень важная, не буду вас сегодня грузить чем-то еще, лучше хорошо разобраться в этой. Всем огромной удачи и пока! Вступайте в нашу группу Вконтакте Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it. myelectronix.ru «Физика - 10 класс» При решении задач, связанных с расчётом работы и мощности тока, надо применять формулы (15.13) и (15.15) - смотри предыдущие темы. Для определения силы тока в замкнутой цепи надо использовать закон Ома для полной цепи, а в случае нескольких источников правильно определить суммарную ЭДС. Задача 1. Аккумулятор с ЭДС Ε = 6,0 В и внутренним сопротивлением r — 0,1 Ом питает внешнюю цепь с сопротивлением R = 12,4 Ом. Какое количество теплоты Q выделится во всей цепи за время t = 10 мин? Р е ш е н и е. Согласно закону Ома для замкнутой цепи сила тока в цепи равна Количество теплоты, выделившейся на внешнем участке цепи, Q1 = I2Rt, на внутреннем — Q2 = I2rt. Полное количество теплоты Задача 2. Разность потенциалов в сети зарядной станции равна 20 В. Внутреннее сопротивление аккумулятора, поставленного на зарядку, равно 0,8 Ом; в начальный момент времени его остаточная ЭДС равна 12 В. Какая мощность будет расходоваться станцией на зарядку аккумулятора при этих условиях? Какая часть этой мощности будет расходоваться на нагревание аккумулятора? Р е ш е н и е. При зарядке аккумулятора зарядное устройство и аккумулятор соединены разноимёнными полюсами навстречу друг другу. Сила тока, идущего через аккумулятор, I = (U - Ε)/R. Мощность, расходуемая станцией: Р1 = UI = U(U - Ε)/R = 200 Вт. Мощность, расходуемая на нагревание аккумулятора: Тогда Р2/Р1 = 0,4. Задача 3. При подключении вольтметра сопротивлением RV = 200 Ом непосредственно к зажимам источника он показывает U = 20 В. Если же этот источник замкнуть на резистор сопротивлением R = 8 Ом, то сила тока в цепи I2 = 0,5 А. Определите ЭДС и внутреннее сопротивление источника. Р е ш е н и е. По закону Ома для полной цепи в первом случае сила тока во втором случае Показания вольтметра — падение напряжения на его внутреннем сопротивлении, т. е. U = I1RV. Из соотношения I1(RV + r) = I2(R + r) найдём внутреннее сопротивление источника: Для ЭДС источника запишем: Ε = I2(R + r) = 24 В. Задача 4. Определите силу тока короткого замыкания для источника, который при силе тока в цепи I1 = 10 А имеет полезную мощность Р1 = 500 Вт, а при силе тока I2 = 5 А — мощность Р2 = 375 Вт. Р е ш е н и е. Сила тока короткого замыкания Полезная мощность Р = IU, где U — напряжение на зажимах источника, или падение напряжения на внешнем участке цепи. Напряжения на зажимах источника в первом и во втором случаях Вычтем почленно из первого выражения второе: откуда определим ЭДС источника тока Окончательно для силы тока короткого замыкания Задача 5. Конденсатор ёмкостью 2 мкФ включён в цепь (рис. 15.12), содержащую три резистора и источник постоянного тока с ЭДС 3,6 В и внутренним сопротивлением 1 Ом. Сопротивления резисторов R1 = 4 Ом, R2 = 7 Ом, R3 = 3 Ом. Чему равен заряд на правой обкладке конденсатора? Р е ш е н и е. Участок цепи, в котором находится конденсатор, разомкнут, и ток через резистор R3 не идёт. Разность потенциалов между пластинами конденсатора равна падению напряжения на резисторе R2: U = IR2. Сила тока, идущего по цепи, согласно закону Ома равна Заряд на обкладках конденсатора На правой обкладке конденсатора накопится отрицательный заряд, так как она подключена к отрицательному полюсу источника. Задача 6. Определите параметры источника тока, если известно, что максимальная мощность, равная 40 Вт, выделяется при подключении резистора сопротивлением 10 Ом. Р е ш е н и е. Максимальная мощность выделяется при равенстве внешнего и внутреннего сопротивлений, следовательно, R = r = 10 Ом. Мощность определяется формулой Р = I2R, или с учётом закона Ома: Тогда ЭДС источника Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский Законы постоянного тока - Физика, учебник для 10 класса - Класс!ная физика Электрический ток. Сила тока --- Закон Ома для участка цепи. Сопротивление --- Электрические цепи. Последовательное и параллельное соединения проводников --- Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» --- Работа и мощность постоянного тока --- Электродвижущая сила --- Закон Ома для полной цепи --- Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи» Вверх class-fizika.ru В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока. Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению. I = U/ R Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника. Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции. U = I*R R = U / I Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление. Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи. Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими. I = E/ Rвн+r Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника. Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными. Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид: I = U/ R = f1 – f2 + E/ R Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети R – общее сопротивление нелинейного участка цепи ЭДС нелинейного участка цепи бывает больше нуля или меньше. Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС. При имеющейся в сети емкости или инертности, необходимо учитывать при проводимых вычислениях, что они выдают свое сопротивление, от действия которого ток приобретает переменный характер. Закон Ома для переменного тока выглядит так: I = U/ Z где Z – сопротивление по всей длине электрической сети. Его еще называют импеданс. Импеданс составляют сопротивления активного и реактивного характера. Закон Ома не является основным научным законом, а лишь эмпирическим отношением, причем в некоторых условиях оно может не соблюдаться: В свою очередь элементы и проводники, соблюдающие закон Ома, называются омическими. Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос – почему на них не действует электрический ток? Объясняется это довольно просто. Птицы, сидя на проводах, представляют собой своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, а та доля, что приходится на сами «проводники» не представляет для них опасности. Но это правило работает лишь при единичном соприкосновении. Если птица заденет клювом или крылом провод или телеграфный столб, она неминуемо погибнет от огромного количества напряжения, которое несут в себе эти участки. Такие случаи происходят повсеместно. Поэтому в целях безопасности в некоторых населенных пунктах установлены специальные приспособления, защищающие птиц от опасного напряжения. На таких насестах птицы находятся в полной безопасности. Закон Ома также широко применятся на практике. Электричество смертельно опасно для человека при одном лишь касании к оголенному проводу. Но в некоторых случаях сопротивление человеческого тела может быть разным. Так, например, сухая и неповрежденная кожа обладает большим сопротивлением к воздействию электричества нежели рана или кожа, покрытая потом. В следствие переутомления, нервного напряжения и опьянения, даже при небольшом напряжении тока человек может получить сильный удар током. В среднем, сопротивление тела человека – 700 Ом, значит, для человека является безопасным напряжение в 35 В. Работая с большим напряжением, специалисты используют специальные средства защиты. infoelectrik.ru
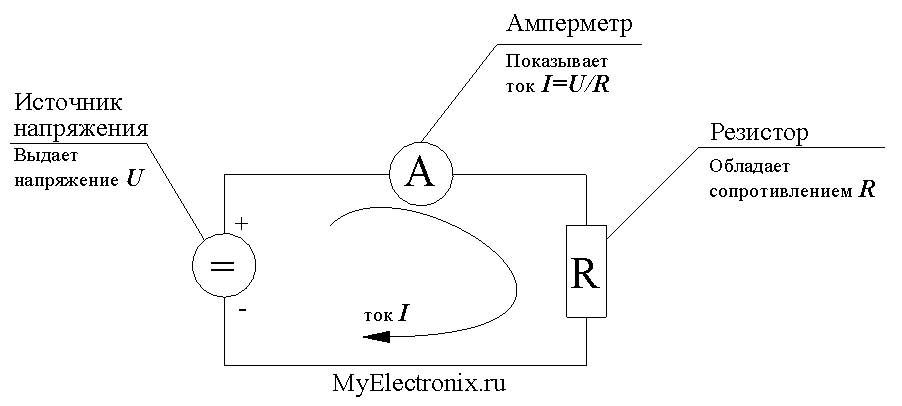
Сила тока в проводнике равна разности потенциалов (напряжению) между концами проводника, делённой на сопротивление проводника.
Здесь Единица измерения силы тока – А (ампер). Указанная формула верна для участка цепи, в котором напряжение постоянно (сила тока тоже будет постоянной). Для полной цепи формула усложняется: Где ru.solverbook.com Закон Ома для полной цепи переменного тока. Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае: Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: Сдвиг фаз в цепи переменного тока определяется характером нагрузки: Мощность в цепи переменного тока. Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): или, переходя к действующим значениям, Величина коэффициент мощности Резонанс в электрической цепи. Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии Следовательно, Амплитуды колебаний напряжения на индуктивности и емкости будут равны и - т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). Следовательно, Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением При этом если величина то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа В случае резонанса Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). www.eduspb.com Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка. Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам: или Коэффициент пропорциональности назвали электропроводностью, а величину принято именовать электрическим сопротивлением проводника. Закон Ома был открыт в 1827 году. Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления Закон Ома для участка электрической цепи имеет вид: где: Закон Ома также применяется ко всей цепи, но в несколько изменённой форме: где: Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: где: Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1). Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред. Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными: где: При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда. Закон Ома можно просто объяснить при помощи теории Друде Wikimedia Foundation. 2010. dic.academic.ruОбъединение учителей Санкт-Петербурга. Закон ома мощность тока
Закон Ома
Единицы измерения в электронике. Закон Ома.
Единицы измерения в электронике
Физическая величина Аббревиатура Единицы измерения Символ единиц измерения Сопротивление R ом Ом, ? Емкость С фарад Ф Индуктивность L генри Гн Напряжение U (V или Е) вольт В Ток I ампер А Мощность Р ватт Вт Частота f герц Гц Число Название Экспоненциальное представление Префикс Аббревиатура 1000000000 1 миллиард 109 Гига Г 1000000 1 миллион 106 Мега м 1000 1 тысяча 103 кило к 100 1 сотня 102 10 1 десяток 101 1 один 100 0,1 1 десятая 10-1 0,01 1 сотая 10-2 0,001 1 тысячная 10-3 милли м 0,000001 1 миллионная 10-6 микро мк 0,000000001 1 миллиардная 10-9 нано н 0,000000000001 1триллионная 10-12 пико п Выводы из закона Ома

Расчеты с применением больших и малых величин
Мощность и закон Ома
Закон Ома


![]() .
.
![]() .
.
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»





Устали? - Отдыхаем!


Законы Ома для участка цепи и для полной цепи
 В 1826 году немецкий ученый Георг Ом совершил открытие и описалэмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
В 1826 году немецкий ученый Георг Ом совершил открытие и описалэмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.Закон Ома для участка цепи
Закон Ома для замкнутой цепи
Закон Ома для неоднородного участка цепи
Закон Ома для переменного тока

Похожие статьи
Формула закона Ома
ОПРЕДЕЛЕНИЕ ![Rendered by QuickLaTeX.com \[ I = \frac{U}{R} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9319a66bd5b1ef25613db639101302ab_l3.png)
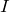 – сила тока,
– сила тока, 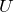 – напряжение,
– напряжение, 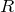 – сопротивление. Это равенство называют законом Ома для участка цепи.
– сопротивление. Это равенство называют законом Ома для участка цепи.
![Rendered by QuickLaTeX.com \[ I = \frac{\epsilon}{R + r} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2524ec68c7956935a9fb702b67daf2f5_l3.png)
 – электродвижущая сила (ЭДС) источника питания,
– электродвижущая сила (ЭДС) источника питания,  – внутреннее сопротивление источника питания, а
– внутреннее сопротивление источника питания, а 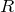 – сопротивление всех внешних элементов цепи. Это равенство называют законом Ома для полной цепи. Из этой формулы следует, что ЭДС источника равна сумме падений напряжения в самом источнике и во внешней цепи.
– сопротивление всех внешних элементов цепи. Это равенство называют законом Ома для полной цепи. Из этой формулы следует, что ЭДС источника равна сумме падений напряжения в самом источнике и во внешней цепи.Примеры решения задач по теме «Закон Ома»
ПРИМЕР 1 Задание
Найти силу тока, если напряжение на участке цепи с сопротивление 5 кОм равно 100 В.
Решение
Напомним, что 5 кОм = 5 000 Ом. Подставим численные значения в формулу:
![Rendered by QuickLaTeX.com \[ I = \frac{U}{R} = \frac{100}{5000} = 0,02 (A) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a82735fd0c24cde5266c6aabb3e9f034_l3.png)
Ответ
Сила тока в цепи равна 0,02 ампера.

Понравился сайт? Расскажи друзьям!
Закон Ома для цепи переменного тока. Мощность в цепи переменного тока. Резонанс в электрической цепи.

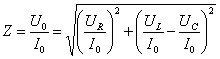 - полное сопротивление переменному току.
- полное сопротивление переменному току. 
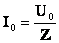
 .
. 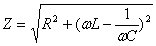
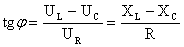 или
или 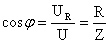 .
. 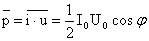
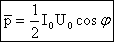
 .
. 
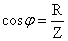 наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.
наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. 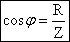

 или
или 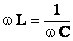 .
. 
 - т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.
- т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре. 
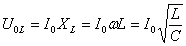
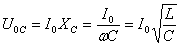
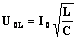
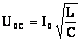
 .
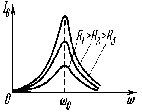
. 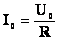 . В этом и состоит смысл явления резонанса.
. В этом и состоит смысл явления резонанса.  ,
, 
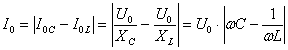 .
. 
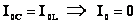 . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов. Ома закон - это... Что такое Ома закон?
Ток, А Напряжение, В Сопротивление, Ом Мощность, Вт I U R P История закона Ома
Закон Ома в интегральной форме
Закон Ома в дифференциальной форме
Закон Ома для переменного тока
Объяснение закона Ома
См. также
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''











Поделиться с друзьями: