Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление. Последовательное соединении резисторов - это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи. На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них. Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле: R = R1 + R2 + R3 То есть, в нашем случае общее сопротивление цепи будет равно: R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм. Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов. Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3). Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них: Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом: В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В. В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения: Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора: Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы: Необходимо рассчитать падение напряжения на выводах "А" и "В": а) без подключенного резистора R3 б) с подключенным резистором R3 Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке. Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором: Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) - то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R). www.joyta.ru Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции. При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго – с началом третьего и т.д. Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: Rобщ = R1 + R2. Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: VRn = IRn x Rn. Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение. При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов. Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной зависимости с сопротивлением резистора. В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора. На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым. В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи. electric-220.ru Господа, наш сегодняшний материал посвящен рассмотрению последовательного соединения резисторов. На практике сплошь и рядом соединяют резисторы друг с другом тем или иным способом для достижения той или иной цели, поэтому весьма важно хорошо разбираться в этом вопросе. Начинаем сразу с определений. Всего есть два вида соединения сопротивлений: последовательное и параллельное. Взгляните на рисунок 1, там наглядно представлены эти виды соединений. А) – Последовательное соединение В) – Параллельное соединение Рисунок 1 – Последовательное и параллельное соединение Что мы видим на рисунке 1? А то, что последовательное соединение – это такое соединение, при котором конец первого резистора совпадает с началом второго, конец второго с началом третьего и т.д. Параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел. В этой статье мы попробуем подробнее проанализировать на основе уже имеющихся знаний последовательное сопротивление. Параллельное же будет в другой статье. Взглянем на рисунок 2. Там подробно разрисовано положение дел для последовательного соединения резисторов. Рисунок 2 – Последовательное соединение резисторов Господа, как вы видите из рисунка 2, при последовательном соединении резисторов у нас нет никаких узлов в схеме. То есть ток нигде никуда не ответвляется. Из этого можно сделать вывод, что при последовательном соединении резисторов через все резисторы течет один и тот же ток I. То есть этот ток величиной I втекает в первый резистор R1, проходит через всю цепочку, вытекает из резистора R3 и течет дальше. При этом его величина неизменна для всех резисторов. С напряжением все не так просто. Сейчас нам понадобиться вспомнить статью про потенциалы. Положим, что на входе резистора R1 у нас потенциал φ1, точка соединения резисторов R1 и R2 имеет потенциал φ2, точка соединения резисторов R2 и R3 имеет потенциал φ3, а конец резистора R3 имеет потенциал φ4. Короче, лучше смотрите рисунок 2, там все эти потенциалы нарисованы Сложим левые и правые части этих трех уравнений. Получим Ну и общее напряжение на всех трех резисторах тоже запишем через разность потенциалов Сравнивая это выражение и предыдущее, приходим к выводу, что Да, приложенное к цепочке последовательно соединенных резисторов напряжение равно сумме напряжений на всех резисторах этой цепочки. Напряжение делится между всеми резисторами: на каком-то оно будет побольше, на каком-то поменьше. А в сумме оно будет равно приложенному к цепочке напряжению. Рассмотрим пример. Допустим, что к нашей цепочке из трех резисторов проложено напряжение U=100 В. Значит, возможна ситуация, когда на резисторах R1, R2 и R3 падает 20 В, 37 В и 43 В (в сумме тоже 100 В). А ситуация, когда на резисторах R1, R2 и R3 падает 50 В, 44 В и 78 В (в сумме 172 В) невозможна. Точно также невозможна ситуация, когда на них падает 10 В, 13 В и 32 В (в сумме 55 В). То есть, если к цепочке последовательно соединенных резисторов приложено 100 В, то суммарное напряжение на всех резисторах тоже должно быть 100 В – не больше и не меньше! Как же именно распределено напряжение между резисторами? Ответ на этот вопрос даст все тот же закон Ома, который не раз нас уже выручал! Согласно закону Ома напряжение на резисторе равно произведению силы тока через него на сопротивление этого резистора. Мы знаем сопротивление данного резистора и ток через него. Поэтому легко находим напряжения на всех резисторах Едем дальше. Воспользуемся этими соотношениями соотношением и с помощью них преобразуем нашу формулку с суммами напряжений. При этом помним, что через все резисторы у нас течет один и тот же ток I. Разделим левую и правую часть уравнения на I: Все та же статья про закон Ома говорит нам, что сопротивление равно напряжение разделить на ток. Поэтому мы можем записать где R – общее сопротивление нашей цепи из трех резисторов. Итак, господа, мы получили важное соотношение: при последовательном соединении резисторов общее сопротивление схемы равно сумме отдельных сопротивлений. Запомните это соотношение, оно весьма важное! В чем же его практический смысл? Взгляните на рисунок 3 Рисунок 3 – Последовательное соединение На нем показано, что цепочку из нескольких (в данном случае из 3-х) последовательно соединенных резисторов для упрощения расчетов вполне можно заменить одним резистором с сопротивлением, равным сумме отдельных резисторов. В связи с этим выводом возможно возникновение вопроса: а зачем вообще на практике соединяют резисторы последовательно, если в конечном счете все можно свести к одному резистору? Господа, причин несколько и основные мы сейчас рассмотрим. 1) Резисторы соединяются последовательно в схемах так называемых делителей напряжения. Кто знает, что это такое – отлично, кто нет – чуть позже разберемся в этом вопросе 2) Последовательное сопротивление резисторов сплошь и рядом применяется в высоковольтной технике. Господа, к резистору можно прикладывать безболезненно для него отнюдь не бесконечно большое напряжение. Максимально допустимое напряжение, которое можно приложить к резистору, всегда прописывается в документации на данный конкретный резистор и его обязательно надо принимать в расчет при выборе резистора в своей схеме. В большинстве своем предельное напряжение ограничено несколькими десятками-сотнями вольт. А как быть, если мы имеем дело с напряжением в тысячи или десятки тысяч вольт? Правильно, резисторы можно соединить последовательно. Как мы помним, при таком соединении общее приложенное напряжение распределяется между резисторами и на каждый из них придется только часть общего. Рассмотрим конкретный пример. Скажем, у нас есть высоковольтный источник, который формирует напряжение 5 кВ. И нам надо подобрать под него такую нагрузку, чтобы обеспечить ток в 1 мА. Будем применять резисторы Р1-12-0,25. Это резисторы, рассчитанные на поверхностный монтаж, и они выдерживают напряжение 200 В. Рассчитаем требуемое количество резисторов как отношение напряжения 5 кВ к максимальному напряжению на один резистор 200 В. При расчете обязательно будем использовать коэффициент запаса равный, скажем, 1,25. Это очень примерная и часто компромиссная величина, но какой-то он обязательно должен быть, никогда нельзя работать на пределе. Итак, нам надо использовать Теперь остается только лишь найти сопротивление каждого резистора в этой цепочке В принципе, этот номинал резистора доступен в номинальном ряду Е192 и его можно купить. Если же именно такого номинала нет в наличии, то берется ближайший доступный и после этого пересчитывается общее сопротивление и при необходимости уточняется количество резисторов. В заключении надо обязательно проверить, какая мощность будет выделяться на каждом из резисторов в такой схеме. Как мы помним из статьи про мощность ее можно посчитать, например, так: Один резистор Р1-12-0,25 без проблем рассеивает 0,25 Вт, то есть нашим резисторам перегрев не угрожает. Итак, для обеспечения тока в 1 мА у источника с напряжением 5 кВ требуется использовать 32 резистора Р1-12-0,25-156 кОм. Мда, что-то я увлекся рассказом про высоковольтные нагрузки 3) Последовательное соединение резисторов можно использовать для распределения мощности источника. Иными словами, мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на последовательно соединенных резисторах. В этом легко убедиться. Надеюсь, вы еще не забыли вот это выражение? Умножим левую и правую части на ток I Или, другими словами где Р – мощность, выдаваемая источником; P1 – мощность, рассеиваемая на резисторе R1; P2 – мощность, рассеиваемая на резисторе R2; P3 – мощность, рассеиваемая на резисторе R3; Как это можно применить? Допустим вот так. Нам, скажем, нужно 1 Вт мощности для обогрева домика нашему хомячку в зимние холода, или еще для чего-то, не важно. У нас на руках есть только резисторы Р1-12-0,25, которые, как мы помним, выдерживают только 0,25 Вт. Как же снять с источника питания 1 Вт без вреда для резисторов? Как вариант, соединив последовательно 4 резистора, подобрав их так, что бы на каждом было 0,25 Вт. В сумме на них будет выделяться как раз-таки 1 Вт. Конечно, помня про коэффициент запаса, лучше брать не 4, а хотя бы 5 резисторов, рассеивая на каждом не 0,25, а 0,2 Вт. Не надо работать на пределе, пусть будет какой-то запас всегда. Наверняка, можно придумать еще варианты применений последовательного соединения резисторов, но, основные мы рассмотрели. Спасибо что прочитали, огромной вам всем удачи и – пока! Вступайте в нашу группу Вконтакте Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it. myelectronix.ru Если несколько резисторов (или приемников энергии) соединены один за другим без разветвлений (рис. 1) и по ним проходит один и тот же ток, то они образуют одну ветвь, такое соединение резисторов называется последовательным. R = R1+R2+R3…+Rn; (1) U = U1+U2+U3…+Un; (2) I = I1 = I2 = I3 = In; (3) P = P1 + P2 +P3…+Pn; (4) Доказательство Согласно закону Ома напряжения на резисторах или падения напряжения определяются выражениями U1 = I*R1; U2 = I*R2; U3 = I*R3; U4 = I*R4; Таким образом, падения напряжения на последовательно соединенных резисторах пропорциональны значениям их сопротивлений. Так же мы знаем что при последовательном соединении напряжение на всём участке цепи равно сумме падения напряжения на каждом элементе последовательной цепи. U = U1+U2+U3…+Un; (2) Ряд последовательно соединенных резисторов можно заменить эквивалентным (общим) сопротивлением R, причем так, чтобы эта замена при неизменном напряжении на выводах соединения не вызвала изменения тока в цепи. Разделив на ток правую и левую части уравнения (2), получим откуда следует, что эквивалентное сопротивление ряда последовательно соединенных резисторов равно сумме их сопротивлений. Из предыдущего выражения, умножая его на I², находим, что R1*I² + R2*I² +R3*I² +Rn*I² = R*I²; P1 + P2 + P3 + Pn = P ; т. е мощность, развиваемая в эквивалентном резисторе, равна сумме мощностей всех резисторов. При последовательном соединении резисторов ток в них один и тот же, поэтому мощности, развиваемые в отдельных участках (P = R*I²), пропорциональны их сопротивлениям. electrikam.comНапряжение при последовательном и параллельном соединении резисторов. Мощность при последовательном соединении резисторов
Последовательное соединение резисторов. Схема соединения и примеры расчета
Последовательное соединение резисторов
Пример № 1
Пример № 2
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Подведем итог
Напряжение при параллельном и последовательном соединении резисторов
Содержание: Напряжение при последовательном соединении
Напряжение при параллельном соединении
Последовательное соединение резисторов
. Дальше вспомним утверждение, что напряжение – это разность потенциалов. То есть разность потенциалов между концами резистора R1 – это напряжение на резисторе R1, ну и так для всех. Запишем это
.
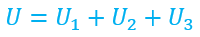
По закону Ома (зная напряжение источника и ток, который необходимо обеспечить) рассчитываем, какое суммарное сопротивление должно быть у этой цепочки резисторов.
. Это можно объяснить тем, что одно время я плотно работал в отделе разработки высоковольтной техники. Это были очень крутые годы 
. Есть что вспомнить, есть что рассказать. Немного жаль, что обстоятельства вынудили сменить место работы, но и попробовать себя в новой области тоже интересно…ладно, едем дальше!
Последовательное соединение сопротивлений (резисторов) | Электрикам
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''
Поделиться с друзьями: