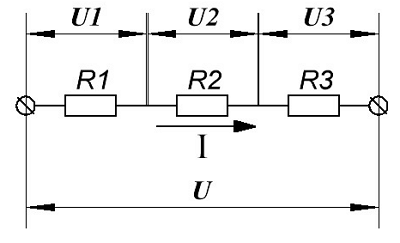
Формулы тоэ I. Тепловая мощность формула через эдс

57.3 Зарядка конденсатора от источника постоянной ЭДС.

Рассмотренный ранее процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.

рис. 546 Пусть незаряженный конденсатор (qo = 0) емкостью подключают к источнику, ЭДС которого равна Ε (рис. 546). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим R. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе UC = q/C и резисторе UR = IR равна ЭДС источника

что приводит к уравнению

В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи I = Δq/Δt, что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени

С таким уравнением мы познакомились в математическом ведении, оно совпадает с уравнением (М13). В соответствии с проведенным математическим анализом, преобразуем его к виду

Из этого уравнения следует, что заряд конденсатора (и пропорциональное ему напряжение) плавно возрастает от начального нулевого до конечного стационарного значения

При этом напряжение на конденсаторе становится равным ЭДС источника. При достижении этого стационарного значения ток в цепи прекратится. Формула для характерного времени зарядки следует из уравнения (3):

Это время совпадает со временем разрядки конденсатора. Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (4) запишем уравнения для малых изменений входящих величин

Так как ЭДС источника постоянна, то ее изменение равно нулю

Сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Δ, поэтому полученное уравнение приобретает вид

Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда I = Δq/Δt):

Для однозначного решения этого уравнения необходимо задать начальное условие − значение силы тока в начальный момент времени Io = I(0). В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна

Очередной раз мы встречаемся с уравнением такого типа − переход к стационарному состоянию! Анализ решения мы проводили неоднократно, поэтому ограничимся графиками зависимости напряжения на конденсаторе и силы тока в цепи от времени показаны на рис. 547.

рис. 547 Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника. На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q, то сторонние силы совершили при этом работу

при этом энергия конденсатора стала равной

что в два раза меньше работы совершенной источником. Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Покажем, что качественные рассуждения верны и количественно. Мысленно разобьем время зарядки на малые промежутки Δti (i = 1, 2, 3, …). Перепишем уравнение (1) в виде

и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Δti, Δqi = IiΔti. В результате получим

Здесь обозначено qi − заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:

работа сторонних сил по перемещению порции заряда Δqi;

увеличение энергии конденсатора при увеличении его заряда на Δqi;

количество теплоты, выделившееся на резисторе, при протекании порции заряда Δqi. Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки. Просуммируем слагаемые выражения (8) по всем промежуткам времени зарядки, в результате чего получим:

полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора;

энергия заряженного конденсатора; наконец,

количество выделившейся на резисторе теплоты. Принимая во внимание уравнение (6) и формулу (М10) из «математического введения», последнюю сумму можно выразить в виде

Эту же сумму можно вычислить и на основании физических законов. Количество выделившейся теплоты равно работе сил электрического поля по преодолению сопротивления резистора. Для малой порции протекающего заряда Δq эта работа равна δA = URΔq, где UR = IR − напряжение на резисторе. Это напряжение не является постоянным в процессе зарядки, его изменение описывается уравнением (1). Построим график зависимости напряжения на резисторе от заряда конденсатора (рис. 548),

рис. 548 который является прямой линией. Заметив, что площадь под графиком равна количеству выделившейся теплоты, получим, что

Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энергии конденсатора и количества выделившейся теплоты A = WC + Q. Схематически преобразование энергии в этом процессе показано на рис. 549.

рис. 549 Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энергии конденсатора. То есть, половина энергии источника переходит в энергию электрического поля, а вторая в тепловую энергию, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора1. Построим гидравлический аналог рассмотренного процесса зарядки конденсатора. Итак, нам необходимо закачать с помощью поршневого насоса вязкую жидкость в вертикальный цилиндрический сосуд.

рис. 550 Запишем уравнение, описывающее движение жидкости по трубке, соединяющей насос с сосудом

где

гидростатическое давление столба жидкости в сосуде, V − объем жидкости, закачанной в сосуд. Если к этому уравнению добавить выражение для расхода жидкости J = ΔV/Δt, то … на этом изложение можно закончить, так как опять придется переписать все слова и формулы, описывающие заряд конденсатора! Предоставим это проделать в качестве упражнения для самостоятельной работы. Рассмотрим только преобразование энергии в этом процессе: − переписываем уравнение (1*) в виде

− мысленно разбиваем процесс на малые промежутки времени Δti; − умножаем уравнение (7*) на малый объем жидкости ΔVi и суммируем:

− вычисляем суммы и даем им физическую интерпретацию (V − конечный объем жидкости в сосуде, H − высота уровня этой жидкости):

работа, совершенная насосом;

потенциальная энергия жидкости в сосуде;

количество теплоты, выделившейся при протекании жидкости по соединительной трубке. − делаем выводы: закон сохранения энергии выполняется, причем половина энергии, преданной насосом запасается в сосуде, половина теряется в виде теплоты. Видимо, основной результат решение задачи о заполнении сосуда жидкостью служит обоснованием финансовой политики многих государств. Покупая бензин на заправке, вы платите примерно в два раза больше, чем реальная стоимость бензина, вторая половина вашей платы − государственный налог! 1Но эти параметры цепи определяют время процесса.

fizportal.ru

2. Работа, мощность и тепловое действие тока.

ЗАКОН ДЖОУЛЯ-ЛЕНЦА

На однородном участке цепи, к которому приложена разность потенциалов () и по которому течет токI, силы электрического поля за время t совершают работу по переносу положительного заряда от точки с высоким потенциалом к точке с низким потенциалом2:

. (25)

В соответствии с законом Ома эту работу можно выразить через сопротивление участка R:

. (26)

Если проводник неподвижен и в нем не совершаются химические превращения, то по закону сохранения энергии работа затрачивается на увеличение внутренней энергии проводника и он нагревается, т. е.

. (27)

Работа A и количество теплоты Q в СИ измеряются в джоулях (Дж).

Мощностью P называется работа, совершаемая в единицу времени. Мощность в СИ измеряется в ваттах (Вт) и определяется по выражению:

. (28)

В замкнутой цепи с источником ЭДС работа по перемещению положительных зарядов равна сумме работы сил электрического поля и работы сторонних сил:

. (29)

В случае замкнутой цепи работа консервативных сил электрического поля равна нулю, поэтому

. (30)

В соответствии с законом Ома для замкнутой цепи формулу (30) можно выразить через сопротивление нагрузки R и внутреннее сопротивление источника r:

. (31)

Полная мощность замкнутой цепи определяется по выражению:

. (32)

Полезная мощность выделяется во внешней цепи (в нагрузке) и рассчитывается по формуле (28).

Д. Джоулем и независимо от него Э. Ленцем было экспериментально установлено, что количество теплоты Q, выделяющейся при протекании электрического тока силой I в проводнике сопротивлением R за время t, определяется по уравнению:

. (33)

Если сила тока изменяется со временем, то

. (34)

Мощность, развиваемая источником, называется полной, она частично выделяется на нагрузке (полезная мощность), частично – на подводящих проводах и на внутреннем сопротивлении (потери мощности).

При передаче электроэнергии от электростанции потребителю часть ее выделяется в виде тепла в подводящих проводах, при этом напряжение на шинах электростанции представляет собой сумму напряжения на проводах и напряжения на нагрузке (потребителе). Коэффициент полезного действия

, (35)

где и A  полезная и совершенная работа.

Если соединить последовательно два проводника с разными сопротивлениями, то сила тока в них будет одинаковая. Тогда в соответствии с формулой

(36)

в проводнике с бóльшим сопротивлением будет выделяться большее количество теплоты (это следует учитывать при включении электронагревательных приборов  электроплиток, чайников и т. д.). Сопротивление подводящих проводов Rпров должно быть значительно меньше сопротивления прибора R, при этом падение напряжения на подводящих проводах будет пренебрежимо мало и все напряжение сети будет приложено к прибору. Следовательно, для расчета количества тепла, выделяемого прибором, необходимо пользоваться формулой:

(37)

Если в цепь включено очень малое сопротивление по сравнению с сопротивлением приборов и подводящих проводов, то падение напряжения на таком сопротивлении незначительно и ток в цепи определяется лишь сопротивлением проводов и приборов. В этом случае для расчета количества теплоты, выделяющейся на этом малом сопротивлении (например, плавком предохранителе), следует пользоваться формулой:

. (38)

Если сопротивление прибора неизвестно, то, определяя силу тока I, протекающего через него, и напряжение на его контактах U, вычисляют количество теплоты по формуле:

. (39)

При решении задач на тепловое действие тока и передачу электроэнергии необходимо:

1) начертить схему и указать на ней все элементы цепи;

2) установить, какие элементы включены последовательно, а какие – параллельно;

3) при соединении приборов помнить следующее:

а) при параллельном соединении на зажимах всех приборов напряжение будет одинаковым и наибольшая мощность будет на приборе с наименьшим сопротивлением;

б) при последовательном соединении сила тока будет одинаковой во всех приборах и наибольшая мощность будет на приборе с наибольшим соп-ротивлением;

4) учитывать, что при передаче электроэнергии на расстояние используется двухпроводная линия, т. е. длина провода в два раза больше расстояния, на которое передается электроэнергия;

5) знать формулы калориметрии (например,  количество теплоты, необходимое для нагревания вещества массой m и удельной теплоем-

костью c от температуры t1 до температуры t2;  количество теплоты, необходимое для плавления вещества массой m и удельной теплотой плавления ).

studfiles.net

формулы тоэ продолжение | энергетик

В разделе: электрический ток (I, ампер), электродвижущая сила (ЭДС, E=A/q=Дж/Кл=В, вольт), электрическое напряжение (U, вольт), электрическая энергия и мощность (Eq, Дж, джоуль) и ватт (Р, Вт, ватт).

Величина электрического тока (I) определяется как количество заряда q переносимое через какую-либо поверхность в единицу времени, при одинаковых промежутках времени t переносимого заряда q, где I = q/t, то такой ток постоянный. I = q/t = Кл/с = А (ампер):

2. Электродвижущая сила (ЭДС). Участок цепи, на котором действует ЭДС, является источником электрической энергии (энергии движущихся носителей электрических зарядов). Единицу ЭДС можно получить как E = A/q = Дж/Кл = В (вольт):

3. Электрическое напряжение (U). На участках электрической цепи, где отсутствует ЭДС, движение носителей зарядов сопровождается расходом полученной ранее энергии путём преобразования её в другие виды. Этот процесс можно охарактеризовать падением напряжения или просто напряжением U, где U = A/q. В случае движения зарядов в безвихревом электрическом поле это определение идентично понятию разности потенциалов участков электрической цепи, т.е. Uab = φа − φb, где , φа, φb, – потенциалы границ участка. Единица измерения напряжения и разности потенциалов такая же, как и ЭДС.

4. Электрическая энергия и мощность. Из понятия ЭДС следует, что она является работой, совершаемой при перемещении единичного заряда между полюсами источника электрической энергии Wи = Eq = EIt, где требуется совершить работу в q раз большую для перемещения всех зарядов, т.е. затратить энергию.

Напомним для тех кто знал но забыл, что такое Электрическая цепь:Электрическая цепь представляет собой совокупность технических устройств и физических объектов, по которым протекает электрический ток, т.е. происходит упорядоченное направленное движение электрических зарядов. Для того чтобы заряды перемещались им необходимо передать некоторую энергию и устройство, выполняющее эту функцию, называется источником электрической энергии. Источник электрической энергии является составным элементом электрической цепи. Энергия, передаваемая источником движущимся зарядам, может быть получена только путём преобразования других видов энергии (тепловой, химической, механической, световой) или путём воздействия на электрические заряды магнитным полем, возбуждаемым другим источником. Создаваемый источником электрический ток может вызывать различные явления: нагревать элементы, по которым он протекает, вызывать свечение веществ, создавать механические усилия. Технические устройства, в которых получают требуемый эффект от протекания электрического тока называют приёмниками электрической энергии, т.к. в них происходит преобразование электрической энергии в другие виды.

Иными словами электрическая цепь состоит из отдельных частей (объектов), выполняющих определенные функции и называемых элементами цепи. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками (потребителями) электрической энергии, о чём собственно и сказано в формулах тоэ выше.

energetik.com.ru

Каталог товаров