Под активной мощностью трехфазной системы понимают сумму активных мощностей фаз нагрузки и активной мощности сопротивления, включенного в нулевой провод: Реактивная мощность трехфазной системы представляет собой сумму реактивных мощностей фаз нагрузки и реактивной мощности сопротивления, включенного в нулевой провод: Полная мощность Если нагрузка равномерная, то где - угол между напряжениемна фазе нагрузки и токомфазы нагрузки. Для измерения активной мощности трехфазной системы в общем случае (неравномерная нагрузка и наличие нулевого провода) необходимо включать три ваттметра, как показано на рис.73. Активная мощность системы равна сумме показаний трех ваттметров. Если нулевой провод отсутствует, то измерение мощности производят двумя ваттметрами по схеме на рис.74. Сумма показаний двух ваттметров при этом определяет активную мощность всей системы независимо от того звездой или треугольником соединена нагрузка. Показание первого ваттметра равно , второго - Но так как . Пример 24. В схеме на рис.75 э.д.с. фаз генератора Требуется определить показания ваттметров и, проверить баланс активных мощностей. В данном примере для сокращения записей обозначим . Тогда По методу двух узлов Напряжение на фазе А нагрузки Ток фазы А (совпадает по фазе с , т.е. имеет нулевую начальную фазу). Напряжение на фазе В нагрузки Ток фазы В A. К ваттметру приложено напряжение, т.е.(см. диаграмму на рис.68), к ваттметру-напряжение Показание первого ваттметра: Показание второго ваттметра: Суммарная активная мощность генератора: Активная мощность нагрузок: C учетом погрешности вычислений баланс активных мощностей выполняется. Пример 25. Определить показания ваттметров в схеме предыдущего примера, если произошёл обрыв фазы C приёмника. К линейному напряжению в таком случае подключены последовательноR и L, следовательно Показания ваттметров: Баланс активных мощностей: Определение последовательности чередования фаз в трехфазной симметричной системе э.д.с. (напряжений) можно осуществить с помощью простейшей схемы из двух ламп накаливания и конденсатора, показанной на рис.76 (емкостное сопротивление конденсатора здесь должно быть равно активному сопротивлению лампы накаливания). Зададимся численными значениями величин: и определим напряжения на фазах нагрузки. Обозначим Напряжения на фазах B и С нагрузки: Из полученных численных данных можно заключить, что лампа в фазе В будет гореть ярко, а в фазе С - тускло. Следовательно, если фазу трехфазной системы э.д.с,, к которой подключен конденсатор, принять за фазу А, то фаза, к которой окажется подключенной ярко горящая лампа, есть фаза В, а фаза с тускло горящей лампой - фаза С. Рассмотрим вопрос, каким будет магнитное поле катушки, по которой протекает синусоидальный ток. Используем для пояснения рис.77, на котором схематично показан разрез катушки. Рис.77 Магнитное поле характеризуется вектором магнитной индукции В. Направление В определяется направлением намотки катушки и направлением тока в данный момент времени. Если ток входит в начало катушки (это направление тока будем считать положительным, ему соответствует интервал времени от 0 до , то вектор магнитной индукции направлен вверх. В следующий полупериод, когда ток отрицателен, вектор В направлен вниз. Таким образом, геометрическим местом концов вектора В является ось катушки. То есть синусоидальный ток создает пульсирующее магнитное поле, вектор магнитной индукции которого изменяется (пульсирует) вдоль оси катушки. Далее предположим, что три одинаковые катушки расположены так, что их оси смещены на 120° по отношению друг к другу, как показано на рис.78, а. Присоединим катушки к симметричной трехфазной системе э.д.с. Пусть токи входят в начала катушек (начала обозначены буквой Н, а концы - К) и изменяются следующим образом: Графики токов изображены на рис.78, б. Каждый из токов создает пульсирующее поле, направленное вдоль оси своей катушки. Положительное направление оси первой катушки обозначим +1, второй +2, третьей +3, магнитную индукцию первой катушки обозначим второй -, третьей -. На рис.79 изобразим мгновенные значения и результи-рующую индукциюдля моментов времени а) б) Рис.78 С увеличением времени вектор результирующей магнитной индукции, оставаясь по величине равным 1,5 Вm, вращается с угловой скоростью по направлению от начала первой катушки с токомк началу второй катушки с током Можно сказать, что вектор результирующей магнитной индукции вращается в сторону катушки с отстающим током. Если ток пропускать по третьей, а ток- по второй катушке, то направление вращения поля изменится на обратное. Вращающееся магнитное поле используется в электрических двигателях переменного тока. Наиболее распространенным в промышленности типом двигателя переменного тока является трехфазный асинхронный двигатель. В нем имеется неподвижная часть - статор, и пазах которого помещены три катушки, создающие круговое вращающееся магнитное поле, и подвижная часть - ротор, в пазах которого находятся три замкнутых на себя или на внешнее сопротивление катушки, схематично устройство асинхронного двигателя в разрезе дано на рис.80. Ротор Статор Рис.80 Ротор4.3. Активная, реактивная и полная мощности трехфазной системы. Активная реактивная и полная мощность трехфазной цепи
4.3. Активная, реактивная и полная мощности трехфазной системы.
4.4. Указатель последовательности чередования фаз
4.5. Получение кругового вращающегося магнитного поля
Допустим, что сначала ротор неподвижен. При этом вращающееся магнитное поле, созданное обмотками статора, пересекает провода катушек неподвижного ротора с угловой частотой и наводит в них э.д.с. Э.д.с. вызовут токи в катушках ротора. По закону Ленца, эти токи стремятся своим магнитным полем ослабить вызвавшее их магнитное поле.
Механическое взаимодействие токов ротора с вращающимся магнитным полем приведет к тому, что ротор начнет вращаться в ту же сторону, в какую вращается магнитное поле.
В установившемся режиме частота вращения ротора составляет (0,98...0,95). Двигатель называют асинхронным потому, что ротор его вращается не синхронно с вращающимся полем;не может равняться угловой частоте вращающегося поля. Это станет понятно, если учесть, что привращающееся поле не пересекало бы провода катушек ротора, в них отсутствовал бы ток и ротор не испытывал бы вращающего момента.
studfiles.net
3.4. Активная, реактивная, комплексная и полная мощности трехфазной симметричной системы
Активной мощностью (часто просто мощностью) трехфазной системы называется сумма активных мощностей всех фаз источника энергии, равная сумме активных мощностей всех фаз приемника.
В симметричной трехфазной системе, т.е. в системе с симметричными генератором и приемником, при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковые. В этом случае Р = 3Рф и для каждой из фаз справедлива формула активной мощности синусоидального тока (2.55):
Pф = UфIфcosj,
где j — угол сдвига фаз между фазными напряжением и током.
Заменив действующие значения фазных тока и напряжения линейными при соединении фаз источника энергии и приемника звездой [см. (3.8), (3.9)] и треугольником [см. (3.14), (3.15)], получим одно и то же выражение для активной мощности симметричной трехфазной системы:
FORMULA! (3.16)
В промышленных установках приемники обычно симметричные или почти симметричные, т. е. мощность может быть вычислена по (3.16).
В общем случае реактивной мощностью трехфазной системы называется сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника. Реактивная мощность симметричной трехфазной системы по (2.58)
Qф = 3Qф = 3UфIsinj,
или после замены действующих значений фазных тока и напряжения линейными
FORMULA! (3.17)
Комплексной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника.
Полная мощность симметричной трехфазной системы
FORMULA! (3.18)
3.5. Сравнение условий работы приемника при соединениях его фаз треугольником и звездой
Схема соединения трех фаз приемника не зависит от схемы соединения трех фаз генератора. Соединение фаз приемника треугольником часто переключается на соединение звездой для изменения тока и мощности, например для уменьшения пусковых токов трехфазных двигателей, изменения температуры трехфазных электрических печей и т. д.
Рассмотрим, как изменяются действующие значения токов симметричного приемника с полным фазным сопротивлением zф при переключении фаз со звезды на треугольник, например, простым трехполюсным переключателем (рис. 3.10).
При соединении фаз приемника звездой между действующими значениями фазных и линейных токов (3.9) и напряжений (3.8) справедливы соотношения
FORMULA!
из которых следует, что
FORMULA! (3.19)
При соединении фаз приемника треугольником между действующими значениями фазных и линейных токов (3.14) и напряжений (3.15) справедливы соотношения
FORMULA!
из которых следует, что
FORMULA! (3.20)
Сопоставив выражения для действующих значений линейных токов при соединении фаз приемника звездой (3.19) и треугольником (3.20), получим при одном и том же действующем значении линейного напряжения Uл и одинаковых полных фазных сопротивлениях zф
IлD = 3IлY, а для действующих значений фазных токов
Активная мощность трехфазного симметричного приемника при любой из схем соединения по (3.16) равна
FORMULA!
Вследствие уменьшения действующего значения линейного тока при переключении фаз приемника с треугольника на звезду мощность уменьшается в 3 раза, т. е.
PD = 3PY. (3.21)
studfiles.net
7.5. Мощность в трехфазных цепях
Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками.
Активная мощность трехфазной цепи равна сумме активных мощностей фаз
(7.5)
Формула (7.5) используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.
При симметричной нагрузке:
При соединении в треугольник симметричной нагрузки
При соединении в звезду
.
В обоих случаях .
3.7. Коэффициент мощности и способы его повышения
Площади поперечного сечения приводов линий электропередачи и электрических сетей, обмоток электрических машин, трансформаторов, электротехнических аппаратов и приборов выбираются, исходя из нагревания, по значению тока в них, который при заданном напряжении переменного тока прямо пропорционален полной мощности S. А энергия, преобразуемая из электрической в другие виды (в механическую, тепловую и т. д.) и используемая в большей части для практических целей, пропорциональна активной энергии и соответствующей ей активной мощности Р.
Как известно, между указанными мощностями и реактивной мощностью существуют соотношения
P = S cos φ; S = √P2 + Q2 .
Входящий в первое выражение cos φ называется коэффициентом мощности и показывает, какую часть полной мощности составляет активная мощность: cos φ = P/S= Р/√P2 + Q2.
Считая, что активная мощность установки, значение которой зависит в основном от мощности приемников, остается постоянной, выясним, к чему приведет увеличение коэффициента мощности установки.
Как следует из приведенных формул, при увеличении cos φ мощность S уменьшается. При Р = const это может происходить лишь за счет уменьшения реактивной мощности Q установки. Снижение мощности S приводит к уменьшению линейного тока Iл . Последнее будет сопровождаться уменьшением потерь напряжения и мощности в сопротивлениях проводов сети, обмотках трансформаторов и генераторов.
Очевидно, при уменьшении тока площади поперечного сечения названных элементов могут быть также уменьшены. В отношении трансформаторов и генераторов это приводит к уменьшению габаритных размеров, расхода дефицитных материалов на изготовление, массы, номинальной мощности и стоимости.
В действующей установке повышение cos φ при существующей площади поперечного сечения проводов позволит увеличить число приемников, которые могут быть подключены к данной сети.
Таким образом, повышение коэффициента мощности дает определенные выгоды во многих отношениях, а поэтому имеет большое народнохозяйственное значение.
Большая часть элементов электрических цепей переменного тока потребляет кроме активной мощности также индуктивную мощность. К ним относятся в первую очередь наиболее распространенные в народном хозяйстве асинхронные электродвигатели. Значительная часть индуктивной мощности потребляется трансформаторами, широко используемыми вразличных установках. Индуктивная мощность потребляется также различными электромагнитными аппаратами, такими, например, как электромагниты, контакторы и магнитные пускатели, реле и т. д.
Для уменьшения индуктивной мощности и увеличения тем самым cos φ необходимо прежде всего:
выбирать правильно двигатели по мощности, так как необоснованное завышение мощности приведет к их работе с недогрузкой, а при этом, как правило, cos φ понижается;
заменять двигатели, работающие с недогрузкой, двигателями меньшей мощности;
сокращать по возможности времена работы двигателей и трансформаторов вхолостую.
Если все же cos φ оказывается недостаточно высоким, прибегают часто к его искусственному повышению. Для этой цели подключают к трехфазной сети компенсирующие устройства, к которым относятся батареи конденсаторов и трехфазные синхронные компенсаторы (см. гл. 11). Последние применяются реже. Батарея конденсаторов соединяется обычно треугольником, как показано на рис. 3.18, а. Батарея конденсаторов потребляет емкостную мощность, которая частично компенсирует индуктивную мощность установки, в результате чего реактивная мощность уменьшается, а коэффициент мощности повышается. Естественно, что cos φ самих приемников при этом остается прежним.
| Рис. 3.18. Схема и векторная диаграмма к примеру 3.5 |
Чтобы уменьшить ток проводов сети, батарею конденсаторов устанавливают по возможности вблизи приемников.
Пример 3.5. К трехфазной сети рис. 3.18, а с линейными напряжениями Uл = 220В подключены два трехфазных приемника. Активная мощность и коэффициент мощности первого приемника P1 = 10 кВт, cos φ1 = 0,7. Фазные сопротивления второго приемника rф = 6 Ом, xLф = 8 Ом, нагрузка симметричная.
Определить токи, мощности и коэффициент мощности cos φ установки из двух приемников. Найти мощность, токи и емкость батареи конденсаторов, если требуется повысить коэффициент мощности до cos φ' = 0,95. Определить токи и мощности установки из двух приемников и батареи конденсаторов.
Решение. Полная и реактивная мощности первого приемника
S1 = P1/cos φ1 = 14,3 кВ•А, Q1 = √S12 - P12 ≈ 10,2 квар.
Полное сопротивление и ток фазы второго приемника
z2 = √r22 + x2L2 = 10 Ом; Iф2 = Uф /z2 = Uл /z2 = 22 А.
Активная и реактивная мощности второго приемника
Р2 = 3I2ф2r2 = 8,7 кВт; Q2 = 3Iф2xLф ≈ 11,6 квар.
Активная, реактивная и полная мощности установки, состоящей из двух преемников.
Р = P1 + P2 =18,7 кВт; Q = Q1 + Q2 = 21,8 квар;
S = √P2 + Q2 ≈ 28,7 кВ•А.
Линейный ток и коэффициент мощности установки из двух приемников
Iл = Ia = S√3Uл ≈ 75,5 A; cos φ = P/S ≈ 0,65.
Мощности установки из приемников и батареи конденсаторов
Р' = Р = 18,7 кВт; S' = P/cos φ' = 19,68 кВ•А;
Q' = √S'2 - P'2 = 6,13 квар.
Линейные токи установки из приемников и батареи конденсаторов, мощность и линейные токи батареи конденсаторов
I'л = I'a = S√3Uл = 51,7 A; Qк = Q - Q' =15,67 квар;
Iк.л = Qк /√3Uл = 41,2 А.
Фазные токи и сопротивление фазы батареи конденсаторов
Iк.л/√3 = 20,8 А; xк.ф = Uф /Iк.ф = Uл /Iк.ф = 10,58 Ом.
Емкость одной фазы и всей батареи конденсаторов
Ск.ф =1/2π/хк.ф = 30 мкФ; Ск = 3Ск.ф = 90 мкФ.
Векторная диаграмма цепи рис, 3.18, а приведена на рис. 3.18, б. На диаграмме показаны только те токи, которые определяют ток I'a (t. е. Ia и Iкa), а также токи, определяющие ток Iкa (т. е. Iкab и Iкca).
20. Основные понятия и принципы анализа переходных процессов в электрических цепях.
studfiles.net
Активная, реактивная и полная мощности трехфазной симметричной системы
Активной мощностью (часто просто мощностью) трехфазной системы называется сумма активных мощностей всех фаз источника энергии, равная сумме активных мощностей всех фаз приемника.

Схемы измерения активной мощности в трехфазной цепи.
В симметричной трехфазной системе, т. е. системе с симметричными генератором и приемником, при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковые. В этом случае Р= 3Рф и для каждой из фаз справедлива формула активной мощности синусоидального тока Рф= UфIф cos?, где ? - угол сдвига фаз между фазными напряжением и током.
Заменив действующие значения фазных тока и напряжения линейными при соединении источника энергии и приемника по схеме "звезда" и "треугольник", получим одно и то же выражение для активной мощности симметричной трехфазной системы:
Р =3UфIфcos?=?3UлIлcos.

Схема разложения несимметричной системы на три симметричных составляющих.
В промышленных установках приемники обычно симметричные или почти симметричные, т. е. мощность может быть вычислена по приведенной выше формуле.
В общем случае реактивной мощностью трехфазной системы называется сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника. Реактивная мощность симметричной трехфазной системы
Q= 3Qф =3UфIфsin
или, после замены действующих значений фазных тока и напряжения линейными,
Q = ?3UлIлsin
Полной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника.
http://fazaa.ru/www.youtube.com/watch?v=vilGgiopbVo
Полная мощность симметричной трехфазной системы - S=?3UлIл.
Поделитесь полезной статьей:
Topfazaa.ru
тест трехфазн ток
Тест 5 трехфазные цепи
Карточка № 5.6
Активная, реактивная и полная мощности трехфазной цепи. Коэффициент мощности
| В симметричной трехфазной цепи фазное напряжение равно 220 В фазный ток 5 A, cosφ = 0,8. Определить активную мощность | О,88 кВт | 5 |
| 1,1 кВт | 58 | |
| 2,64 кВт | 40 | |
| Найти реактивную мощность трехфазной цепи в условиях предыдущей задачи | 0,66 квар | 97 |
| 1,1 квар | 27 | |
| 2,64 квар | 70 | |
| 1,98 квар | 49 | |
| В симметричной трехфазной цепи линейное напряжение равно 220 В, линейный ток 5 А, коэффициент мощности 0,8.Определить активную мощность | 1,1 кВт | 13 |
| 1,14 кВт | 81 | |
| 1,52 кВт | 56 | |
| Подсчитать реактивную мощность трехфазной цени в условиях предыдущей задачи | 0,38 квар | 35 |
| 1,14 квар | 94 | |
| 1,1 квар | 21 | |
| 1,52 квар | 67 | |
| В трехфазной цени линейное напряжение равно 220 В, линейный ток 2 А, активная мощность 380 Вт. Найти коэффициент мощности | 0,8 | 42 |
| 0,6 | 92 | |
| 0,5 | 7 | |
| 0,4 | 65 |
Карточка № 5.4
Назначение нулевого провода в четырехпроводной цепи
| Может ли геометрическая сумма линейных токов быть отличной от нуля при отсутствии нулевого провода? | Может | 1 |
| Не может | 2 | |
| Будут ли меняться линейные токи при обрыве нулевого провода в случае: а) симметричной нагрузки; б) несимметричной нагрузки? | а) Будут; б) не будут | 1 |
| Будут | 2 | |
| а) Не будут; б) будут | 3 | |
| Не будут | 4 | |
| За счет чего могут измениться линейные токи при постоянной ЭДС генератора и неизменных сопротивлениях нагрузки? | Изменения линейных напряжений | 1 |
| Изменения фазных напряжений | 2 | |
| Изменения фазных и линейных напряжений | 3 | |
| Чему равна разность потенциалов точек О и О' при наличии нулевого провода сопротивлением R0? | 0 | 1 |
| I0R0 | 2 | |
| U0 | 3 | |
| Может ли нулевой провод, обладающий большим активным сопротивлением, обеспечить симметрию фазных напряжений при несимметричной нагрузке? | Может | 1 |
| Не может | 2 |
Карточка № 5.7
Выбор схем соединения осветительной и силовой нагрузок при включении их в трехфазную сеть
| Лампы накаливания с номинальным напряжением 127 В включают в трехфазную сеть с линейным напряжением 220 В. Определить схему соединения ламп | Звездой | 1 |
| Звездой с нулевым проводом | 2 | |
| Треугольником | 3 | |
| Лампы нельзя включать в сеть с линейным напряжением 220 В | 4 | |
| В ту же сеть включают трехфазный двигатель, каждая из обмоток которого рассчитана на 27 В. Как следует соединить обмотки двигателя? | Звездой | 1 |
| Треугольником | 2 | |
| Двигатель нельзя включать в эту сеть | 3 | |
| Трехфазный двигатель, рассмотренный в предыдущей задаче, включают в сеть с линейным напряжением 380 В. Как нужно соединить обмотки двигателя? | Звездой | 1 |
| Треугольником | 2 | |
| Двигатель нельзя включать в эту сеть | 3 | |
| Лампы накаливания с номинальным напряжением 220. Включают в трехфазную сеть с линейным напряжением 220 В. Определить схему соединения ламп | Звездой | 1 |
| Звездой с нулевым проводом | 2 | |
| Треугольником | 3 | |
| В ту же сеть включают трехфазный двигатель, каждая из обмоток которого рассчитана на 220 В. Как следует соединить обмотки двигателя? | Звездой | 1 |
| Треугольником | 2 |
Карточка № 5.2
Соединение трехфазной цепи звездой. Четырех- и трехпроводная цепи
| Укажите правильное определение фазы | Фазой называют аргумент синуса | 1 |
| Фазой называют часть многофазной цепи | 2 | |
| Оба определения правильны | 3 | |
| Чему равно действующее значение векторной суммы фазных токов? | Сумме действующих значений фазных токов | 1 |
| Меньше суммы действующих значений фазных токов и только в предельном случае равно ей | 2 | |
| Всегда меньше суммы действующих значений фазных токов | 3 | |
| Чему равен ток в нулевом проводе при симметричной трехфазной системе токов? | Нулю | 1 |
| Значению, меньшему суммы действующих значений фазных токов | 2 | |
| Всегда ли векторная сумма токов фаз равняется нулю при отсутствии нулевого провода? | Всегда | 1 |
| Не всегда | 2 | |
| Может ли ток в нулевом проводе четырехпроводной цепи быть равен нулю? | Может | 1 |
| Не может | 2 | |
| Всегда равен нулю | 3 |
Карточка № 5.3
Соотношения между фазными и линейными напряжениями и токами при симметричной нагрузке в трехфазной цепи, соединенной звездой
| Какой из токов в схеме линейный, какой фазный? | Оба тока линейные | 1 |
| Оба тока фазные | 2 | |
| Ток I1— линейный, ток I2 — фазный | 3 | |
| Ток I2 — линейный, ток I1 фазный | 4 | |
| Между различными точками схемы, изображенной выше, включены вольтметры. Какой из них показывает линейное напряжение, какой — фазное? | Напряжение UAO— линейное, напряжение UBO фазное | 1 |
| Напряжение UAB— линейное, напряжение UBC фазное | 2 | |
| Напряжение UCA— линейное, напряжение UCO фазное | 3 | |
| Чему равен вектор UАС, если UAC=UC -UA? | UAC=-UC -UA | 1 |
| UAC= UA- UC | 2 | |
| UAC=UC +UA | 3 | |
| Укажите причину того, что полярная и топографическая векторные диаграммы трехфазной цепи удовлетворяют одной и той же системе векторных уравнений | Уравнения имеют векторную форму | 1 |
| Уравнения написаны для симметричной нагрузки | 2 | |
| Векторы можно переносить параллельно их начальному положению | 3 | |
| Симметричная нагрузка соединена звездой. Линейное напряжение 380 В. Определить фазное напряжение | 380 B | 1 |
| 250 B | 2 | |
| 220 B | 3 | |
| 127B | 4 |
Карточка № 5.5
Соединение нагрузки треугольником. Векторные диаграммы, соотношения между фазными и линейными токами и напряжениями
| Написать уравнения, связывающие векторы линейных и фазных токов | IA=IAB-ICA IB=IBC-IAB IC=ICA-IBC | 1 |
| IA= ICA- IAB IB=IAB- IBC IC= IBC- ICA | 2 | |
| IA= ICA+ IAB IB= IAB+ IBC IC= IBC+ ICA | 3 | |
| Удовлетворяет ли приведенная диаграмма уравнениям токов для изображенной выше схемы? | Да | 1 |
| Нет | 2 | |
| Как соединены эти обмотки? | Звездой | 1 |
| Треугольником | 2 | |
| Звездой с нулевым проводом | 3 | |
| Линейное напряжение 380 В. Определить фазное напряжение, если симметричная нагрузка соединена треугольником | 380 В | 1 |
| 220 В | 2 | |
| 127 В | 3 | |
| Линейный ток равен 2,2 А. Рассчитать фазный ток, если симметричная нагрузка соединена треугольником | 3,8 А | 1 |
| 2,2 А | 2 | |
| 1,27 А | 3 |
Карточка № 5.1
Принцип получения трехфазной ЭДС. Основные схемы соединения трехфазных цепей
| При вращении рамок против часовой стрелки в них индуцируется ЭДС, изображенные на рисунке. Какие ЭДС индуцируются при вращении рамок по часовой стрелке? | Те же самые | 1 |
| Знаки начальных фаз изменятся на противоположные | 2 | |
| Направления векторов ЭДС в рамках изменятся на противоположные | 3 | |
| Изменится ли действующее значение трехфазной ЭДС при изменении направления вращений рамок? | Не изменится | 1 |
| Изменится | 2 | |
| Какие характеристики ЭДС изменятся, если при прочих равных условиях увеличить частоту вращения рамок? | Частота и начальные фазы | 1 |
| Частота и амплитуды | 2 | |
| Амплитуды и начальные фазы | 3 | |
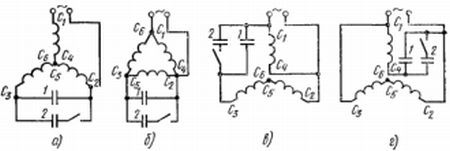
| Сколько соединительных проводов подводят к генератору, обмотки которого образуют звезду? | 6 | 1 |
| 3 или 4 | 2 | |
| 3 | 3 | |
| 4 | 4 | |
| С какой точкой соединяется начало первой обмотки при включении обмоток генератора треугольником? | С началом второй | 1 |
| С концом второй | 2 | |
| С концом третьей | 3 |
studfiles.net



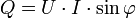







Поделиться с друзьями: