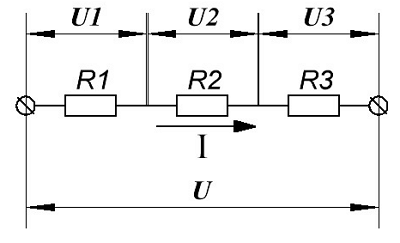
Активная мощность трехфазной системы определяется как сумма активных мощностей фаз нагрузки с учетом активной мощности в сопротивлении нулевого провода: P=PA+PB+PC+P0. Реактивная мощность трехфазной системы определяется аналогично: Q=QA+QB+QC+Q0. Полная мощность несимметричной трехфазной нагрузки равна В симметричной трехфазной системе активную, реактивную и полную мощности можно найти следующим образом: В уравновешенных системах суммарная активная мощность постоянна и не зависит от времени: P=PA+PB+PC=3UфIфcosj=P. В несимметричной трехфазной системе полная, активная и реактивная мощности определяется отдельно для каждой фазы нагрузки: Задание 1. Расчет простых цепей постоянного тока Задание: Схема, составленная из резистивных элементов, питается от источника постоянного напряжения (источник подключен ко входным зажимам «а» и «b», причем положительный полюс источника соединен с зажимом «а»). Рассчитать токи во всех ветвях схемы и падения напряжений на каждом из резисторов. Вариант схемы каждому студенту принять в соответствии с его порядковым номером в списке группы. Параметры элементов схем для каждого варианта приведены в таблице 4.1. Таблица 4.1 Варианты задания и параметры элементов схем При выполнении задания студенту следует вычертить схему в соответствии с заданным вариантом и выписать исходные данные (значения напряжения источника Uab, сопротивлений R1¸R4). Затем необходимо проанализировать схему, определив виды соединения резисторов на отдельных участках схемы (последовательное или параллельное), после чего, постепенно «сворачивая» схему (заменяя последовательное или параллельное соединение резисторов на отдельных участках эквивалентными сопротивлениями), найти эквивалентное сопротивление всей цепи RЭ относительно входных зажимов «а» и «b». После этого следует определить значение тока в неразветвленной части цепи, а затем, постепенно «разворачивая» схему, найти токи в отдельных ветвях схемы и напряжения на каждом из резисторов. Варианты схем для выполнения задания 1 Рис. 4.1 Рис. 4.2 Рис. 4.3 Рис. 4.4 Рис. 4.5 Рис. 4.6 Рис. 4.7 Рис. 4.8 Рис. 4.9 Рис. 4.10 Рис. 4.11 Рис. 4.12 Рис. 4.13 Рис. 4.14 Рис. 4.15 Рис. 4.16 Рис. 4.17 Рис. 4.18 Рис. 4.19 Рис. 4.20 Рис. 4.21 Рис. 4.22 Рис. 4.23 Рис. 4.24 Рис. 4.25 Пример расчета простой цепи постоянного тока. В схеме, изображенной на рис. 4.26, напряжение источника Uab=20 В, сопротивления резисторов равны соответственно: R1=5 Ом, R2=3 Ом, R3=2 Ом, R4=4 Ом, R5=7 Ом. Рассчитать токи во всех ветвях схемы и падения напряжений на каждом из резисторов. Рис. 4.26. Исходная схема для расчета Очевидно, что резисторы R2 и R3 соединены последовательно, поэтому общее сопротивление данной ветви (рис. 4.27, а) можно найти как Резисторы R4 и R5 соединены параллельно, поэтому эквивалентное сопротивление двух этих ветвей (рис. 4.27, а) можно найти как В свою очередь, сопротивления а б в Рис. 4.27. Последовательность отыскания эквивалентного сопротивления Величину эквивалентного сопротивления RЭ всей схемы (рис. 4.27, в) находим как сумму R2345 и R1, так как данные сопротивления соединены последовательно; RЭ=R1+R2345=6,69 Ом. Ток I1 в неразветвленной части цепи может быть найден как Для нахождения остальных токов необходимо знать напряжение на резисторах R4, R5 и R23. Эти резисторы соединены параллельно, поэтому напряжение на них одинаково и равно напряжению на сопротивлении R2345, которое может быть найдено как Токи в параллельных ветвях исходной схемы равны: Проверку полученных результатов можно провести по первому закону Кирхгофа, в соответствии с которым Напряжения на резисторах исходной схемы равны: Задание 2. Расчет сложных цепей постоянного тока Задание: для электрических схем (варианты параметров элементов схем и номера схем для расчета каждым из методов приведены в таблицах 5.1 и 5.2) выполнить следующее: 1. Определить величины и направления токов во всех ветвях схемы по методу уравнений Кирхгофа. 1.1. Вычертить заданную схему, выписать заданные величины э.д.с. и сопротивлений; 1.2. Задать произвольные положительные направления токов в ветвях схемы (индексы токов при этом должны совпадать с индексами сопротивлений в соответствующих ветвях), определить число независимых узлов схемы, определить число независимых контуров схемы и задаться направлениями их обхода; 1.3. Составить необходимое количество уравнений по первому и второму законам Кирхгофа; полученную систему уравнений решить относительно неизвестных токов, определив их величину и истинное направление; 1.4. Произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи. 2. Определить величины и направления токов во всех ветвях схемы по методу контурных токов. 2.1. Вычертить заданную схему, выписать заданные величины э.д.с. и сопротивлений; 2.2. Выбрать независимые контуры, задаться в них произвольными направлениями контурных токов; 2.3. Составить систему уравнений для контурных токов по второму закону Кирхгофа; решить данную систему относительно неизвестных контурных токов; 2.4. Определить значения токов в ветвях схемы через найденные контурные токи; 2.5. Произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи. 3. Определить величины и направления токов во всех ветвях схемы по методу наложения. 3.1. Вычертить заданную схему, выписать заданные величины э.д.с. и сопротивлений; 3.2. Составить частичные схемы замещения исходной схемы; для каждой из частичных схем замещения задать направления токов в ветвях и определить эти токи, пользуясь законами Ома и Кирхгофа. По найденным токам частичных схем замещения найти полные токи в ветвях исходной схемы; 3.4. Проанализировать режимы работы источников э.д.с.; 3.5. Произвести проверку правильности расчета токов путем составления уравнения баланса мощностей цепи. Таблица 5.1. Параметры элементов схем для расчета lektsia.com При симметричной трехфазной нагрузке достаточно определить мощность Рф, потребляемую в одной фазе, так как измеряемая мощность трехфазной нагрузки Р = ЗРФ. Простейшие условия для такого измерения имеются, когда нагрузка соединена звездой с доступной нулевой точкой. В этих случаях цепь тока ваттметра включается последовательно с одной из фаз нагрузки, а цепь напряжения ваттметра включается на напряжение той фазы, ток которой проходит через ваттметр. Схема измерения мощности. Если нулевая точка недоступна или нагрузка соединена по схеме треугольника, применяется искусственная нулевая точка. Так называется нулевая точка звезды, образованной из сопротивления цепи напряжения ваттметраrn.вт и двух других равных ему добавочных сопротивлений:rв иrc. При правильном соединении с искусственной нулевой точкой цепь напряжения ваттметра находится под фазным напряжением и через ваттметр проходит фазный ток. В таких условиях ваттметр измеряет фазную мощность Рф, и мощность трехфазной нагрузки опять определяется посредством умножения показания ваттметра. Обычно завод-изготовитель снабжает ваттметр искусственной нулевой точкой для измерения в трехфазных системах. Схема трех ваттметров. Измерения мощности в трехфазных трехпроводных системах при несимметричной нагрузке в большинстве случаев выполняются по способу двух ваттметров. Своеобразной особенностью этого способа является то обстоятельство, что не только при несимметричной, но даже при симметричной нагрузке показания двух ваттметров в большинстве случаев не равны, а показания одного из ваттметров могут стать отрицательными. Мощность трехфазной системы в этом случае приходится определять как алгебраическую сумму показаний двух ваттметров. Справедливость такого способа доказывается на основании уравнений мгновенной мощности, выраженной через мгновенные значения напряжений и токов. Мгновенная мощность любой фазы равна произведению мгновенных значений фазных напряжений и тока, а мгновенная мощность трехфазной системы равна сумме мгновенных фазных мощностей. Например, при соединении звездой: Но согласно первому закону Кирхгофа при соединении звездой без нулевого провода: Подставив это значение в уравнение мощности, получим: Разность фазных напряжений равна соответствующему линейному напряжению: Следовательно, мощность трехфазной системы может быть выражена суммой двух произведений , а эти два произведения могут быть измерены двумя ваттметрами, включенными в соответствии со схемой метода. Схема способа двух ваттметров. Нет нужды особо доказывать справедливость способа двух ваттметров для соединения треугольником, так как при определенных значениях линейных напряжений и токов мощность не зависит от способа соединения нагрузки. Отметим своеобразную особенность способов двух ваттметров: система линейных напряжений в нормальной последовательности обозначается иАВ, ивс, иСА,а в уравнение этого способа входит напряжение иАС. Такая перестановка индексов обозначает, что по отношению к первому ваттметру нужно изменить фазу напряжения на 180°. Для этого достаточно соединить «начало» (зажим со знаком звездочки) цепи напряжения первого ваттметра с проводом А, а «конец» этой цепи (зажим, у которого указано номинальное напряжение) с проводом С. Распределение мощности трехфазной системы между показаниями двух ваттметров зависит, главным образом, от величины и знака сдвига фаз. Проследим эту зависимость в простейшем случае при симметричной нагрузке. Если вместо мгновенной мощности в уравнение (101) подставить активную (среднюю) мощность трехфазной системы, то необходимо заменить мгновенные значения напряжения и токов действующими и ввести в уравнение косинусы сдвигов фаз между соответствующими напряжениями и токами. Таким образом, уравнение мощности примет следующий вид: При симметричной нагрузке по величине линейные токи: равны между собой так же, как и линейные напряжения: Векторная диаграмма к способу двух ваттметров. На построена векторная диаграмма трехфазной системы, на которой вектор uAC построен равным по величине и противоположным по направлениюиСА На основании этой диаграммы угол сдвига фаз между векторамиuAC иiА и угол сдвига фаз ф2между векторамиивс и iВ будут соответственно ф1 = ф – 30о и ф2 = ф + 30о. Следовательно, показания двух ваттметров, составляющие мощность трехфазной системы, выразятся следующим образом: Это выражение показывает, что при симметричной нагрузке показания ваттметров равны только при ф = 0. Если же ф >60о, то стрелка второго ваттметра отклоняется за нуль шкалы, а чтобы отсчитать в таких условиях показание второго ваттметра, нужно переключить (т. е. поменять местами в схеме) зажимы цепи напряжения прибора. Часто для изменения фазы тока на 180° в цепи напряжения в корпус ваттметра встраивается специальный переключатель. Показания второго ваттметра после переключения следует считать отрицательными, и, чтобы определить мощность трехфазной установки, нужно эти показания вычитать из показаний первого ваттметра. Для измерения мощности в трехфазных четырехпроводных системах простейшим является способ трех ваттметров. В каждый из линейных проводов включается цепь тока одного из ваттметров, а цепь напряжения каждого из ваттметров включается между соответствующим линейным проводом и нулевым проводом системы. При таком соединении каждый из ваттметров измеряет мощность одной фазы системы. Следовательно, активная мощность всей трехфазной системы будет равна простой сумме показаний трех ваттметров: В промышленных установках на распределительных щитах широко применяются ваттметры трехфазного тока. Они представляют собой два (для трехпроводной системы) или три (для четырехпроводной системы) измерительных механизма, связанных общей осью и таким путем воздействующих на общую стрелку. Эти измерительные механизмы включаются в трехфазную цепь соответственно способу двух ваттметров или способу трех ваттметров. Поделитесь полезной статьей: fazaa.ru Активная мощность, отдаваемая трехфазным генератором и потребляемая трехфазным потребителем, определяется суммой активных мощностей каждой фазы потребителя: Аналогичное определение можно отнести и к реактивной мощности трехфазного тока, т. е. Полная, мощность трехфазного потребителя равна Очевидно, что при равномерной нагрузке фаз ( Однако на практике удобней оперировать линейными величинами, так как доступными являются линейные провода, а не обмотки генератора или двигателя. При соединении потребителя звездой при равномерной нагрузке фаз Тогда При соединении потребителей треугольником при равномерной нагрузке фаз Тогда Таким образом, при равномерной нагрузке фаз при соединении потребителей звездой и треугольником мощности трехфазного тока определяются выражениями: активная мощность реактивная мощность полная, мощность или при неравномерной нагрузке по (16.27) При неравномерной нагрузке фаз полная, или кажущаяся, мощность трехфазного тока может быть определена суммой полных мощностей каждой фазы, выраженной в комплексной форме, а именно Равномерную нагрузку в трехфазных цепях обеспечивают электрические двигатели трехфазного тока, обмотки которых могут быть соединены или звездой, или треугольником. Мощность в трехфазных системах. Мощность трехфазной нагрузки
Мощность в трехфазных системах.
⇐ ПредыдущаяСтр 5 из 5 .
.
 A =
A =  АН
АН A = PA + jQA = UAHIA cosjA + jUAHIA sinj;
A = PA + jQA = UAHIA cosjA + jUAHIA sinj; B =
B =  ВН
ВН B = PB + jQB = UBHIB cosjB + jUBHIB sinj;
B = PB + jQB = UBHIB cosjB + jUBHIB sinj; C =
C =  СН
СН C = PC + jQC = UCHIC cosjC + jUCHIC sinj;
C = PC + jQC = UCHIC cosjC + jUCHIC sinj; 0 =
0 =  00’
00’ 0 = P0 + jQ0 = U00’I0 cosj0 + jU00’I0 sinj.
0 = P0 + jQ0 = U00’I0 cosj0 + jU00’I0 sinj. Вари-ант
Схема (№ рис.)
Значения сопротивлений резисторов, Ом
Напряжение источника, В
R1 R2 R3 R4 1
2
3
4
5
6
7
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.18
4.19
4.20
4.21
4.22
4.23
4.24
4.25
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
1
2
3
4
5
6
7
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.18
4.19
4.20
4.21
4.22
4.23
4.24
4.25


























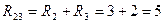 Ом.
Ом. Ом.
Ом. и
и  между собой соединены параллельно, поэтому их можно заменить сопротивлением
между собой соединены параллельно, поэтому их можно заменить сопротивлением  (рис. 4.27, б):
(рис. 4.27, б): 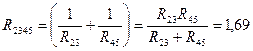 Ом.
Ом.
 А.
А. В.
В. А,
А, А,
А, А.
А.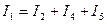 . Подстановка чисел в данное выражение дает 2,99 А = 2,99 А. Токи определены верно.
. Подстановка чисел в данное выражение дает 2,99 А = 2,99 А. Токи определены верно. В,
В, В,
В, В,
В, В.
В. Схема (№ рисунка)
Вариант параметров
Параметры элементов схемы
Е1, В
Е2, В
R1, Ом
R2, Ом
Измерения мощности в трехфазных трехпроводных системах




Мощность трехфазного тока
 (16.25)
(16.25) (16.26)
(16.26) (16.27)
(16.27) и
и  ) активная мощность трехфазного тока равна утроенному значению активной мощности каждой фазы
) активная мощность трехфазного тока равна утроенному значению активной мощности каждой фазы (16.28)
(16.28) , а
, а 

 , а
, а 

 (16.29)
(16.29) (16.30)
(16.30) (16.31)
(16.31)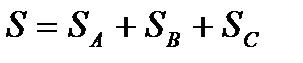 (16.32)
(16.32)Похожие статьи:
poznayka.org









Поделиться с друзьями: