На участке цепи с параллельным соединением резистора, индуктивной катушки и конденсатора (рис.2.21) может возникнуть резонанс токов . Условием возникновения такого режима является равенство реактивных проводимостей bL=bC. Рисунок 2.21 – Участок цепи с параллельным соединением резистора, индуктивной катушки и конденсатора При резонансе токов полная проводимость цепи становится чисто активной и равной g, а общий ток цепи Iрез=gU минимальным. Фазовый сдвиг между напряжением и током φ=arcCos(g/y), вносимый цепью, равен нулю. Режим участка цепи, при котором сдвиг фаз между напряжением на его выводах и общим током равен нулю, называется резонансом токов. При резонансе действующие значения токов в катушке и конденсаторе одинаковы: IL=(1/ωрезL)U=IC=ωрезCU, а сдвиг фаз между токами равен π, так как ток в индуктивности отстает от напряжения на π/2, а ток в конденсаторе опережает напряжение на такой же угол π/2. Если при резонансе токов в одинаковое число раз n увеличить индуктивную и емкостную проводимости, то токи IL и IC увеличатся тоже в n раз, а общий ток останется тем же: I=Ug. Таким образом, в принципе можно неограниченно увеличивать токи в индуктивности и емкости при неизменном токе источника. На рисунке 2.22 показаны резонансные кривые параллельного контура. В конденсаторе ток IC=ωCU возрастает пропорционально угловой частоте, в катушке индуктивности ток IL=U/(ωL) обратно пропорционально угловой частоте, в резисторе ток IR=U/R от угловой частоты не зависит. Точка пересечения кривых IC(ω) и IL(ω) соответствует резонансу токов, при котором I=IR=Iрез. Если проводимость g резистора равна нулю, то и полная проводимость y равна нулю. При этом общий ток цепи (ток источника) также равен нулю, что эквивалентно размыканию цепи. Рисунок 2.22 – Резонансные кривые параллельного контура Отметим, что резонанс токов в отличие от резонанса напряжений – явление безопасное для электроэнергетических установок. Резонансные режимы находят широкое применение в радиотехнических устройствах. Как уже говорилось выше, коэффициент мощности определяет, какая часть полной мощности, потребляемой электроустановкой, преобразуется в ней в другие виды энергии (механическую или тепловую), т.е. какую часть от полной мощности, потребляемой установкой, составляет активная мощность: Коэффициент мощности установки, потребляющей электрическую энергию, не остается постоянным: с течением времени изменяется нагрузка двигателей, трансформаторов и других приемников, одни выключаются, друге включаются и т.д. Поэтому мгновенным значением Cosφ характеризовать установку нельзя. Для этой цели вводят понятие средневзвешенного коэффициента мощности за определенный промежуток времени. Он определяется величинами активной и реактивной энергии, подсчитанными за данный промежуток времени: где Wа – активная энергия; Wр – реактивная энергия. Низкий коэффициент мощности электроустановок приводит к нежелательным последствиям. Так при снижении Cosφ для получения заданной величины активной мощности P приходится увеличивать полную мощность источника энергии (S=P/Cosφ). Например, при Cosφ=1 для питания нагрузки Р=100кВт, необходим источник электрической энергии с полной мощностью S=100кВА, а при Cosφ=0,5 для питания той же нагрузки уже S=200кВА. Возрастание полной мощности сказывается во-первых на увеличении первоначальных затрат по ее созданию, и во-вторых приводит к возрастанию абсолютных потерь электроэнергии. Уменьшение коэффициента мощности при заданной величине активной мощности Р вызывает увеличение потребляемого тока: а отсюда возрастают и потери в сети: где Rл – активное сопротивление одного провода линии. При низких значениях Cosφ возрастает полный ток. Снижение же потребляемого тока при повышении Cosφ позволяет включить в сеть дополнительную нагрузку без увеличения мощности генераторов. Кроме того, величина коэффициента мощности, при которой осуществляется эксплуатация генераторов и трансформаторов, оказывает существенное влияние на их КПД. Основными причинами низкого Cosφ являются: Все мероприятия по повышению Cosφ условно можно разделить на три группы: Условно мероприятия первой группы называются естественными, а мероприятия второй и третьей групп – искусственными. К естественным мероприятиям в первую очередь следует отнести следующие: К искусственны мероприятиям следует отнести применение конденсаторных батарей и синхронных компенсаторов, выполняющих роль местных генераторов реактивной энергии. Применение конденсаторных батарей или синхронных компенсаторов для повышения коэффициента мощности наглядно демонстрирует векторная диаграмма, представленная на рисунке 2.23. Рисунок 2.23 – Векторная диаграмма, отражающая применение конденсаторных батарей или синхронных компенсаторов для повышения коэффициента мощности На рисунке 2.23,а показана схема, на которой параллельно приемнику, например, группе асинхронных двигателей, может быть включена конденсаторная батарея. До включения конденсаторов ток Iд отстает по фазе от напряжения на угол φ1. После включения конденсаторной батареи реактивная (индуктивная) составляющая I1р тока двигателей частично компенсируется емкостным током IC (рис. 2.23,б), в связи с чем ток в подводящих проводах уменьшается до I, а угол сдвига фаз – до φ2. При этом активная составляющая тока в проводах не изменяется, следовательно, по активной мощности режим работы цепи остается прежним. Синхронный компенсатор представляет собой синхронный электродвигатель, работающий при перевозбуждении в режиме холостого хода. В таком режиме синхронный двигатель одновременно превращается в генератор реактивной энергии, которая отдается в сеть и обеспечивает компенсацию общего сдвига фаз. Преимущество синхронного компенсатора перед конденсаторной батареей заключается в возможности плавной регулировки потребляемого им реактивного тока. К мероприятиям, допускаемым в виде исключения, относится использование имеющихся синхронных двигателей и генераторов в качестве синхронных компенсаторов. Другие разделы главы 2: chertovlektor.ru Реактивные сопротивления и проводимости отдельных участков цепи могут быть положительными (индуктивные элементы) и отрицательными (емкостные элементы). Поэтому возможны такие сочетания этих элементов, когда входное реактивное сопротивление или входная реактивная проводимость всей цепи равны нулю. При этом ток и напряжение на входе цепи совпадают по фазе и эквивалентное сопротивление всей цепи является активным. Такие режимы цепи называются резонансными. Резонанс напряжений. На рис.2.7 приведена цепь, включающая последовательно соединенные активное сопротивление, индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда индуктивное и емкостное сопротивления одинаковы по величине (рис.2.10). Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения. Ток в резонансном режиме достигает максимума, так как полное сопротивление z цепи имеет минимальное значение: . Условие возникновения резонанса: . Частоту называют резонансной частотой: . (2.46) Из (2.46) следует, что режима резонанса можно добиться следующими способами: изменением частоты; изменением индуктивности; изменением емкости. В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, значительно превышающие напряжение на входе цепи, если реактивные сопротивления значительно превышают активное сопротивление. Напряжение на индуктивности при резонансе равно напряжению на емкости: . Отношение Q называют добротностью контура. Добротность показывает, во сколько раз напряжения на реактивных элементах превышают входное напряжение в резонансном режиме. В радиотехнических цепях добротность составляет несколько сотен. Резонансные свойства характеризуют также величиной обратной добротности , называемой затуханием контура. Волновое сопротивление контура или характеристическое сопротивление определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока: . При резонансе напряжений малые количества энергии, поступающие от источника и компенсирующие потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно больших количеств энергии магнитного и электрического полей. Покажем, что при резонансе в любой момент времени суммарная энергия магнитного и электрического полей остается постоянной: . (2.47) Пусть ток в резонансном контуре , тогда напряжение на емкости отстает по фазе от тока на 900. Суммарная энергия магнитного и электрического полей (2.47) равна: . При резонансе , . Следовательно, const. Если в схеме (рис.2.10) величина ЭДС и параметры R, L, C неизменны, но меняется частота , то изменяется реактивное сопротивлениеX и, следовательно, полное сопротивление угол . Зависимости параметров двухполюсника (действительной и мнимой части входного сопротивления или входной проводимости) от частоты называют частотными характеристиками. Реактивное сопротивление при трех характерных значениях частоты принимает предельные значения, равные нулю, либо бесконечности (рис.2.21). При , при, приимеет место резонанс напряжений иX=0. Аргумент функции, при котором она принимает бесконечное значение, называется полюсом функции, а аргумент, при котором она принимает нулевое значение, называется нулевым значением. Отметим, что в момент резонанса происходит изменение характера реактивного сопротивления: при реактивное сопротивление имеет емкостной характер, а при- индуктивный характер. Рис. 2.21 Величина действующего тока в цепи и напряжения на индуктивности и емкости также зависят от изменения частоты: Зависимости действующих значений тока и напряжений на элементах цепи при изменении частоты называют резонансными кривыми. Резонансные характеристики ,,приведены на рис.2.23. Напряжение на емкости пристремится кU, а при стремится к нулевому значению, напряжение на индуктивностиприравно нулю, пристремится кU. При резонансной частоте и взаимно компенсируются, ток цепи максимален, напряжение источника приложено к активному сопротивлению. Рис. 2.22 Из рис. 2.22 видно, что максимум напряжения на индуктивности и максимум напряжения на емкостиимеют место при частотах не равных резонансной частоте. Максимумимеет место при частоте меньшей, а максимумпри частоте большей. В электроэнергетических устройствах влияние резонанса, как правило, нежелательное, так как при резонансе напряжения на индуктивных и емкостных элементах могут значительно превышать номинальные значения. Такие явления могут возникать при подключении к зажимам синхронного генератора или трансформатора длинной линии передачи или кабеля, не замкнутых на приемник нагрузки. Генератор и трансформатор имеют индуктивное сопротивление, а линия или кабель обладают емкостью и индуктивностью. При отсутствии нагрузки на конце линии затухание такой цепи очень мало и возникают перенапряжения, если частота близка к резонансной. Явление резонанса напряжений широко используется в радиопередающих и радиоприемных устройствах. Резонанс токов. На рис.2.11 приведена цепь, включающая параллельно соединенные активное сопротивление, идеальная индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда реактивная проводимость цепи (рис.2.14). При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. В электрической цепи наступает режим резонанса токов. Из условия возникновения резонанса тока получим формулу для резонансной частоты тока: . Полученное выражение для резонансной частоты совпадает с (2.46). Резонанса токов можно добиться изменением частоты, изменением индуктивности либо емкости. В режиме резонанса тока полная (входная) проводимость цепи - минимальна, а полное сопротивление- максимально. Ток в неразветвленной части схемыв резонансном режиме имеет минимальное значение, в отличие от резонанса напряжений, когда ток имеет максимальное значение. В идеализированном случае приR = 0, и . Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой. При резонансе токов возможны режимы, когда токи через индуктивность и емкость значительно превосходят ток в неразветвленной части схемы. Превышение токов в реактивных элементах над током в неразветвленной части схемы имеет место при условии . Величина имеет размер проводимости и называется волновой проводимостью контура. Добротность контура Q при резонансе токов определяет кратность превышения тока в индуктивности и емкостинад током в неразветвленной части схемы: . Величина обратная добротности является затуханием контура. Энергетические процессы при резонансе токов аналогичны энергетическим процессам при резонансе напряжений. Малые количества энергии, поступающие от источника и компенсирующие потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно больших количеств энергии магнитного и электрического полей. Суммарная энергия магнитного и электрического полей при резонансе токов также в любой момент времени остается постоянной. Частотные характеристики проводимостей ветвей с индуктивностью , с емкостьюи входной проводимостиприведены на рис. 2.23. Рис. 2.23 При , при, приимеет место резонанс токов иb=0. В момент резонанса происходит изменение характера входной проводимости: при входная проводимость имеет индуктивный характер, а при- емкостной характер. Резонансные характеристики ,,при неизменном входном токе (I = const) и неизменных величинах активного сопротивления, индуктивности и емкости (R = const, L=const, C = const) определяются выражениями , , и приведены на рис. 2.24. При сопротивление индуктивности равно нулю и весь ток протекает через катушку,. Присопротивление конденсатора стремится к нулю и ток проходит только через конденсатор,. При частоте резонанса, токи в индуктивности и конденсаторе взаимно компенсируются, входной ток равен току через активное сопротивление. Максимумы токов через индуктивность и емкость не совпадают с максимумом напряжения при резонансной частоте. Максимумимеет место при частоте меньшей, а максимумпри частоте большей. Рис. 2.24 В энергетике процесс уменьшения угла сдвига фаз между напряжением на приемнике и током, потребляемым из сети, называют компенсацией угла сдвига фаз. Входное сопротивление большинства промышленных предприятий имеет индуктивный характер вследствие массового использования асинхронных двигателей. Для уменьшения величины потребляемого тока за счет компенсации его реактивной составляющей и соответственно потерь электроэнергии в сети, параллельно приемнику энергии включают батареи конденсаторов. Экономически выгодно подключать конденсаторы на возможно более высокое напряжение, так как ток через конденсаторы пропорционален напряжению. Компенсация угла сдвига фаз обычно выполняется до значения коэффициента мощностиcos = 0,90,95. studfiles.net Резонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. BL=BC. Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Данная схема соответствует цепи, представленной на рис. 8, а, для которойR2 = 0, а R1=Rк (здесьRк – активное сопротивление катушки индуктивности). Полная проводимость такой цепиY=. Условие резонанса токов (BL=BC) можно записать через соответствующие параметры электрической цепи. Так как реактивная проводимость катушки, имеющей активное сопротивлениеRк, определяется выражениемBL=XL/=L/(Rк2+2L2), а проводимость конденсатора без учета его активного сопротивления (RC= 0)BC=XC/= 1/XC=C, то условие резонанса может быть записано в виде L/(+2L2) = C. Из этого выражения следует, что резонанс токов в такой цепи можно получить при изменении одного из параметров Rк,L,Cипри постоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении указанных параметров. Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала. В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности катушки L, путем изменения емкостиСбатареи конденсаторов. С изменением емкостной проводимостиBC=C, пропорциональной емкости конденсатора, происходит изменение полной проводимостиY, общего токаIи коэффициента мощности cos. Указанные зависимости приведены на рис. 10,a. Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость электрической цепи сначала уменьшается, достигает при (BL=BC) своего минимума, а затем возрастает с увеличениемС, в пределе стремясь к бесконечности. Общий токI=YU, потребляемый цепью, пропорционален полной проводимости. Поэтому характер его изменения подобен характеру изменения проводимости. Коэффициент мощности cosс увеличением емкости сначала возрастает, а затем уменьшается, в пределе стремясь к нулю, так как cos=G/Y. В результате анализа указанных зависимостей можно установить, что резонанс токов характеризуется следующими явлениями. a)б) Рис. 10 1. При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей: Y = =G. 2. Минимальное значение проводимости обусловливает минимальное значение тока цепи: I = YU = GU. 3. Емкостный ток ICи индуктивная составляющаяIL тока катушкиIкоказываются при этом равными по величине, а активная составляющая тока катушкиIа1 становится равной токуI, потребляемому из сети: Iр1 = IL = BLU = BCU = IC = Iр2; Iа = Iа1 =GU = YU =I. При этом реактивные составляющие токов IL иICв зависимости от значений реактивных проводимостей могут приобретать теоретически весьма большие значения и намного превышать токI, потребляемый электрической цепью из сети. 4. Реактивная составляющая полной мощности цепи при BL=BCоказывается равной нулю: Q = BLU2 BCU2 = QL QC = 0. При этом индуктивная и емкостная составляющие реактивной мощности также могут приобретать весьма большие значения, оставаясь равными друг другу. 5. Полная мощность цепи при резонансе равна ее активной составляющей: S = YU 2 = GU 2 = P. 6. Коэффициент мощности всей цепи при резонансе: cos = P/S = GU 2/YU 2 = 1. Напряжение и ток электрической цепи при резонансе токов совпадают по фазе. Векторная диаграмма, построенная для условий резонанса токов и применительно к рассматриваемой цепи, представлена на рис. 10, б. В табл. 2 методических указаний по выполнению работы обозначениямIL, IK, IC соответствуют обозначенияIр1, I1, Iр2 на векторной диаграмме токов (рис. 10,б). Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности, так как это имеет большое технико-экономическое значение. Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер; некоторые из них работают с низким коэффициентом мощности и потребляют значительную реактивную мощность. К таким потребителям могут быть отнесены асинхронные двигатели (особенно работающие с неполной нагрузкой), установки электрической сварки, высокочастотной закалки и т.д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батарей снижает общую реактивную мощность установки и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах за счет снижения его реактивной составляющей и, соответственно, к уменьшению потерь энергии в генераторе и подводящих проводах. studfiles.net В последовательной цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, в зависимости от соотношений XLи XC, можно выделить три характерных режима ее работы при: XL> XC, XL< XC и XL= XC. Построим векторные диаграммы для всех трех случаев (рис. 2.14) Рис. 2.14 Векторные диаграммы режимов работы последовательной цепи переменного тока. Третья векторная диаграмма аналогична диаграмме цепи переменного тока с активным сопротивлением в том смысле, что , напряжение и ток совпадают друг с другом, угол сдвига фаз между ними . Отсутствие влияния реактивных сопротивлений на величину тока в цепи объясняется тем, что при равенстве между собой сопротивлений XL и XC, равные между собой и смещенные относительно друг от друга на 180° напряжения ULи UC взаимно компенсируются. Величина тока в цепи при этом определяется только активным сопротивлением и достигает максимального значения. = I max (2.25) Режим работы последовательной цепи переменного тока, когда XL=XC называется резонансом напряжений. В случае наличия в цепи нескольких индуктивных и емкостных сопротивлений условием достижения резонанса напряжений является равенство: Хотя, при резонансе напряжений, напряжения ULи UCне оказывают влияния на величину тока в цепи, эти напряжения существуют и могут значительно превышать напряжение U, приложенное к зажимам цепи, что и предопределило название этого явления. Действительно Отсюда видно, что при резонансе напряжений, напряжения на индуктивном или емкостном сопротивлениях во столько раз больше напряжения, приложенного к зажимам цепи, во сколько раз индуктивное или емкостное сопротивление больше активного сопротивления цепи. Резонанс напряжений можно вызвать двумя способами: а) изменением емкости конденсаторной батареи; б) изменением частоты питающего тока. а) Если постепенно увеличивать емкость конденсаторной батареи от нуля до некоторого конечного значения, то емкостное сопротивление будет уменьшаться, а ток в цепи возрастать, в соответствии с выражением (2.25), и достигнет наибольшего значения при такой емкости Ср, когда XС окажется равным XL. Дальнейшее увеличение емкости приводит к снижению тока. Сказанное можно проиллюстрировать графиком (рис. 2.15). Рис. 2.15. К определению резонанса напряжений. б) Из условия резонанса напряжений следует , откуда или f р , где fр– резонансная частота тока. Сказанное иллюстрируется графиком (рис. 2.16). Рис. 2.16. К определению резонансной частоты питающего тока Рассмотрим цепь переменного тока, состоящую из двух ветвей, в первую из которых включены активное сопротивление R1 и индуктивное сопротивление XL, а во вторую – активное сопротивление R2 и емкостное сопротивление XC (рис. 2.17). Обе ветви оказываются включенными под одним и тем же напряжением U, равным напряжению, приложенному к зажимам цепи. Рис. 2.17 Схема переменного тока с параллельным соединением R, XL, XC. Под действием напряжения в неразветвленной части цепи возникает ток i , который распределяется по двум параллельным ветвям, обратно пропорционально их сопротивлениям. Составим по первому закону Кирхгофа уравнение мгновенных значений токов В действующих значениях токов уравнение принимает вид: Ток первой ветви, соответственно равны: Ток второй ветви соответственно равны: Ток в неразветвленной части цепи можно определить графически, путем построения векторной диаграммы (рис. 2.18). При параллельном соединении R,XL, XC в качестве базисного вектора выбирается вектор напряжения, т.к. он одинаков для всех ветвей схемы. Относительно этого вектора откладываются вектора токов . Рис. 2.18. Векторная диаграмма цепи переменного тока с параллельным соединением R, XL, XC. Активные и реактивные составляющие токов в ветвях определяются как Активная составляющая общего тока в цепи равна арифметической сумме активных составляющих токов ветвей: Реактивная составляющая общего тока в цепи равна алгебраической сумме реактивных составляющих токов в ветвях: В результате получается треугольник токов АВС (рис. 2.18), из которого получим: (2.26) В общем виде, в параллельных цепях переменного тока величина тока в неразветвленной части цепи определяется по формуле: Кроме того, из треугольника токов можно получить следующие соотношения: Активная мощность цепи с параллельным соединением определяется как арифметическая сумма активных мощностей ветвей: Реактивная мощность цепи определяется как алгебраическая сумма реактивных мощностей ветвей: studfiles.net Количество просмотров публикации РЕЗОНАНС ТОКОВ - 612 Резонанс токов может возникнуть в параллельной цепи (см. рис. 2.17, а), одна из ветвей которой содержит L и r, а другая Си r. Резонансом токов принято называть такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. На рис. 2.17, г изображена векторная диаграмма цепи рис. 2.17, а при резонансе токов. Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, в случае если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю: I1р = I2р. Общий реактивный ток цепи, равный разности реактивных токов ветвей, в данном случае равен нулю: I1р - I2р = 0. Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей: Iа = I1а + I2а . Выразив реактивные токи через напряжения и реактивные проводимости, получим UbL = UbС, откуда bL = bС. Итак, при резонансе токов реактивная проводимость ветви с индуктивностью равна реактивной проводимости ветви с емкостью. Выразив bL и bС через сопротивления соответствующей ветви, можно определить резонансную частоту контура: откуда В идеальном случае, когда r1 = r2 = 0, При резонансе токов коэффициент мощности равен единице: cos φ = 1. Полная мощность равна активной мощности: S = P. Реактивная мощность равна нулю: Q = QL - QC = 0. Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений, которые были подробно рассмотрены в § 2.12. Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью. Рис. 2.19. Электрическая цепь (а) и графики зависимости Ir, IL, IC и I от частоты f (б) Для резонанса токов характерно, что общий ток при определенном сочетании параметров цепи должна быть значительно меньше токов в каждой ветви. К примеру, в идеальной цепи, когда r1 = r2 = 0 (см. рис. 2.18, а), общий ток равен нулю, а токи ветвей с емкостью и индуктивностью существуют, они равны по модулю и сдвинуты по фазе на 180°. Резонанс в цепи при параллельном соединении потребителей принято называть резонансом токов. Резонанс токов должна быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты источника питания при заданных параметpax цепи. Представляет интерес влияние частоты источника питания на значения токов в цепи, к примеру в цепи, изображенной на рис. 2.19, а. Ток в ветви с индуктивностью обратно пропорционален частоте: IL = U/2πfL, а ток в ветви с емкостью прямо пропорционален частоте: IС =U2πfC. Ток в ветви с активным сопротивлением не зависит от частоты 1: Ir = U/r. Вектор общего тока в цепи равен геометрической сумме векторов токов ветвей: Ī =Īr + ĪL+ĪС, 1В случае если пренебречь влиянием вытеснения тока к поверхности проводника. а значение тока При f = 0 IL = ∞; IC = 0; Ir = U/r; I = ∞. При f = fрез IL = IC; I = Ir = U/r. При f → ∞ IL → 0; IC → ∞; Ir = U/r; I → ∞. Графики зависимости Ir, IL, IС и I от частоты изображены на рис. 2.19,б. Большинство промышленных потребителей переменного тока имеют активноиндуктивный характер; некоторые из них работают с низким коэффициентом мощности и, следовательно, потребляют значительную реактивную мощность. К таким потребителям относятся асинхронные двигатели, особенно работающие с неполной нагрузкой, установки электрической сварки, высокочастотной закалки и т. д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батареи уменьшает общую реактивную мощность установки, так как Q = QL - QC , и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах, соединяющих потребитель с источником энергии, и полной мощности источника. Рис. 2.20. Электрическая цепь к примеру 2.5 Пример 2.5. Определить емкость конденсатора, при которой в цепи рис. 2.20 возникает резонанс токов, в случае если xL = 40 Ом, r1 = 30 Ом, r2 = 28 Ом, f = 1000 Гц. Решение. При резонансе токов реактивная мощность цепи равна нулю: QL - QС = 0, или QL = QC . ; ; ; Емкость конденсатора ; . referatwork.ru 18. РЕЗОНАНС ТОКОВ Резонанс токов может возникнуть в параллельной цепи (см. рис. 20а), одна из ветвей которой содержит L и r, а другая – C и r. Рис. 20. Резонанс токов в параллельной цепи Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. На рисунке 20г изображена векторная диаграмма цепи (рис. 20а) при резонансе токов. Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю: I1p = I2p. Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю: I1p – I2p = 0. Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей: Ia = I1a = I2a. В идеальном случае, когда При резонансе токов коэффициент мощности равен единице: cos φ = 1. Полная мощность равна активной мощности: S = P. Реактивная мощность равна нулю: Q = QL– QC= 0. Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений. Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью. Для резонанса токов характерно, что общий ток при определенном сочетании параметров цепи может быть значительно меньше токов в каждой ветви. Например, в идеальной цепи, когда r1 = r2 = 0, общий ток равен нулю, а токи ветвей с емкостью и индуктивностью существуют: они равны по модулю и сдвинуты по фазе на 180°. Резонанс в цепи при параллельном соединении потребителей называется резонансом токов. Резонанс токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты источника питания при заданных параметрах цепи. velib.com Резонанс токов возникает в цепях с параллельным включением индуктивного и емкостного элементов. Рассмотрим электроцепь, схема замещения которой представлена на рис.1. Схема замещения Векторная диаграмма с Рис. 1 параллельными ветвями Рис. 2 Зависимость общего тока цепи от Векторная диаграмма в частоты питающего напряжения момент резонанса токов Рис. 3 Рис. 4 Для этой цепи рассмотрим векторную диаграмму. При резонансе ток i до разветвления совпадает по фазе с напряжениемu (рис.4). Используя проводимость, имеем –реактивная проводимость; –полная проводимость; –активная проводимость. Отсюда видно, что резонанс токов наступает при , т.е. при условии равенства активных составляющих полной проводимости параллельных ветвей цепи. Это означает, что при резонансе токов модули реактивных составляющих токов в параллельных ветвях должны быть равны. Тогда реактивная составляющая тока в цепи до разветвления будет равна нулю. Следовательно, для нашей цепи резонанс наступит при условии или . Решая данное уравнение относительно резонансной угловой частоты получим . В случае, когда сопротивления ималы, и ими можно пренебречь, и резонансная частота параллельной цепи с идеальными реактивными элементами определяется тем же уравнением, что и резонансная частота последовательной цепи. В параллельных цепях L и C энергия магнитного поля передаётся от индуктивного элемента конденсатору, где она переходит в энергию электрического поля; затем энергия электрического поля конденсатора передаётся индуктивному элементу и т.д. Обмен энергией между реактивными элементами происходит непосредственно между параллельными ветвями, минуя источник, в то время при резонансе напряжений обмен энергией осуществляется через источник. Вся энергия от источника выделяется в виде тепла на резисторах и , гдеи – реактивные мощности индуктивного и ёмкостного элементов. Отсюда реактивная мощность цепи , а полная мощность цепи . Зависимость тока I от частоты показана на рис.3, а векторная диаграмма в момент резонанса токов на рис.4. При резонансе токов ток в разветвлённой части цепи имеет наименьшее значение, в то время при резонансе напряжений ток в цепи достигает наибольшего значения. Однако токи в параллельных ветвях при резонансе токов могут значительно превышать ток в неразветвлённой части цепи, чем и объясняется название данного резонанса. Коэффициент мощности показывает, какую часть общей мощности источника составляет полезная (активная) мощность, используемая приёмником. При заданной активной мощности потребителя ток в сети тем меньше, чем больше коэффициент мощности. Наиболее благоприятный момент представляет, когда . Один из способов повышения является подключение параллельно электрическим системам конденсаторных батарей. Основой электроснабжения потребителей электроэнергии является трёхфазная система токов. Она обладает рядом преимуществ. Обеспечивает получение кругового магнитного поля, которое используют в электрических машинах переменного тока, создание двух различных по значению напряжений от общего источника, эффективную передачу электроэнергии на большие расстояния. Трехфазно системой электрических цепей называют систему, в которой действуют три синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинцтые друг относительно друга по фазе на угол (1200) создаваемые общим источником энергии – трехфазным синхронным генератором. Мгновенные значения ЭДС трехфазного источника: , ,, где – начальная фаза ЭДС; – начальная фаза ЭДС. Такая система ЭДС называется симметричной. Временная и векторная диаграммы ЭДС трехфазной симметричной системы Существует два способа соединения обмоток: звездой и треугольником. При соединении обмоток источника питания (генератора, трансформатора) звездой концы обмоток (X, Y, Z) всех трех фаз объединяют в одну общую точку N выводят провода, по которым энергия подается потребителям. Напряжения ,,между линейными проводами называют линейными напряжениями, а токи,,в линейных проводах – линейными токами. Напряжения ,,между нейтральным проводом и соответствующим линейным проводом называют фазными напряжениями Временная и векторная диаграммы фазных напряжений имеет такой же вид, что и диаграммы ЭДС. При соединении обмоток источника питания треугольником объединяют в одну общую точку начало и конец соответствующих фаз: X и C, Y и C, Z и A. В этом случае фазные напряжения равны линейным . Соотнощение между фазными и линейными напряжениями для соединения звездой. Согласно второму закону Кирхгофа уравнения связи между указанными напряжениями в комплексной форме: ,,. Построим на комплексной плоскости векторную диаграмму. соответствующую приведенным уравнениям Векторы линейных напряжений сдвинуты относительно друг друга так же, как и векторы фазных напряжений, на угол и опережают их на угол; векторы,,опережают соответственно векторы,,. Модули все напряжений равны:. Следовательно и модули всех линейных напряжений так же равны. Из треугольника векторной диаграммы, образованного векторами,иследует . Таким образом, при симметричной системе фазных напряжений и соединении обмоток трехфазного источника питания звездой модуль линейного напряжения в раз больше фазного. studfiles.net2.6. Резонанс напряжений. Полная мощность цепи s при резонансе токов равна
Резонанс токов
/ Причины низкого Cosφ и пути его повышения
2.6. Резонансные режимы в цепи. Резонанс напряжения, резонанс токов. Частотные характеристики резонансных цепей
Резонанс токов
2.6. Резонанс напряжений
2.7. Цепь переменного тока с параллельным соединением активного, индуктивного и ёмкостного сопротивлений (параллельная r-l-c цепь).
РЕЗОНАНС ТОКОВ
18. РЕЗОНАНС ТОКОВ | Читать онлайн, без регистрации
Лекция 7 Резонанс токов
Технико–экономическое значение коэффициента мощности и способы его повышения
Лекция 8 анализ трёхфазных электрических цепей Основные схемы трёхфазных цепей, их характеристики и методы расчёта
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''

.jpg)




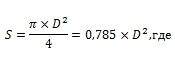





Поделиться с друзьями: