Понятие о законе Ома Итак, давайте предположим, что вы собрали свою первую схему. Вы знаете величину тока, которую компонент схемы может выдержать, не выходя из строя, и напряжение, выдаваемое источником питания. Следовательно, вам нужно рассчитать сопротивление, которое не позволит току в цепи превысить пороговое значение. В начале 1800-х годов Георг Ом опубликовал уравнение, названное впоследствии законом Ома, которое позволяет выполнить такой расчет. Закон Ома гласит: напряжение равняется произведению тока на сопротивление, или (в стандартной математической записи): U = I x R Помните ли вы из школы основы алгебры? Давайте еще раз вспомним вместе: если в уравнении с тремя величинами известны две, то достаточно легко рассчитать третью неизвестную величину. Закон Ома основывается именно на таком уравнении; члены уравнения можно переставлять как угодно, но зная любые два, всегда можно вычислить третий. Например, можно сказать, что ток является частным от деления напряжения на сопротивление: I = U / R Наконец, можно рассчитать сопротивление при известных токе и напряжении, переставив члены того же уравнения: R = U / I Итак, пока вроде бы все ясно. Теперь давайте попробуем проверить наши знания на практике: пусть есть схема, питающаяся от 12-вольтовой батареи, и электрическая лампа (скажем, большой фонарик). Перед установкой лампочки в фонарик вы измерили сопротивление схемы мультиметром и нашли, что оно равно 9 Ом. Вот формула для расчета электрического тока по закону Ома: I = U / R = 12 вольт / 9 Ом = 1,3 A Ну, а что, если вы обнаружили, что лампочка светит чересчур уж ярко? Яркость можно изменить, уменьшив ток, т.е. просто добавив в схему резистор. Изначально мы имели сопротивление схемы 9 Ом; добавив 5-омный резистор в схему, мы повысим ее сопротивление до 14 Ом. В этом случае ток будет равен: I = U / R = 12 вольт / 14 Ом = 0,9 А Предположим, что у вас есть схема с небольшой сиреной, которая имеет сопротивление 2 килоома, а также 12-вольтовая батарея. Для того чтобы рассчитать ток, вам нужно выразить сопротивление цепи не в килоомах, а в базовых единицах — омах, не используя приставку “кило”. В нашем случае это значит, что нужно разделить напряжение на 2000 Ом: I = U / R = 12 вольт / 2000 Ом = 0,006 A В результате мы получили ток, записанный как доля 1 А. После окончания расчета будет удобнее вновь использовать префикс, чтобы дать ответ в более лаконичном виде: 0,006 А = 6 мА Подводя итоги, можно сказать: для проведения расчетов необходимо все исходные величины преобразовать к базовым единицам счисления. Георг Ом (вот уж поистине, наш пострел везде поспел!) также нашел выражение для мощности, вычисляемое при известных напряжении и токе: Р = U х I; или Мощность = напряжение X ток. Это уравнение можно использовать для расчета мощности, потребляемой сиреной из предыдущего примера: Р = 12 В х 0,006 А = 0,072 Вт, или 72 мВт. Ладно, а что же делать, если напряжение на сирене нам не известно? Вы можете заняться простейшим преобразованием формулы для мощности, используя школьные знания (а вы-то думали, что зря протираете штаны на уроках физики!). Поскольку U = I х R, можно подставить это выражение в формулу для мощности, получив Р = I2 х R; или Мощность = квадрат тока х сопротивление. Вы также можете использовать алгебраические преобразования, чтобы самостоятельно прикинуть, как можно рассчитать сопротивление, напряжение или ток, зная мощность и любой другой из этих же параметров. arduinos.by Пусть источник тока создает переменное гармоническое напряжение (рисунок) U(t) = Uosinωt. (1) Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону: I(t) = U(t)/R = (Uo/R)sinωt = Iosinωt, где Io = Uo/R ? амплитудное значение силы тока в цепи.Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.Величины Uo и Io = Uo/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность P(t) = U(t)I(t), которая, в отличие от цепей постоянного тока, изменяется с течением времени.С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде P(t) = U(t)I(t) = I2(t)R = Io2Rsin2ωt. Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.Перепишем формулу для мощности по-другому: P = UI = UoIosin2ωt = (1/2)UoIo(1 ? cos2ωt) = UoIo/2 ? (UoIo/2)cos2ωt. Первое слагаемое не зависит от времени. Второе слагаемое ? переменная составляющая ? функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рисунок).Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле Pcp = UoIo/2 = Io2/R. Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.Поскольку для постоянного тока Pпост =I2R, то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока Iд = Io/?2. Аналогично можно ввести действующее значение и для напряжения Uд = Uo/?2. Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения: P = UдIд = Iд2R = Uд2/R, Iд = Uд/R. 41.1. Треугольники напряжений и сопротивлений. Амплитуды составляющих общего напряжения: Действующие значения: Вектор общего напряжения: Для того, чтобы найти значение вектора U, построим векторную диаграмму (рис. а). За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительнымнаправлением оси, от которой отсчитываются фазовые углы. Вектор Из диаграммы видно, что вектор общего напряжения U опережает вектор тока I на угол Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Ua = Проекция вектора напряжения U на направление, перпендикулярное вектору тока называется реактивной составляющей вектора напряжения и обозначается Up. Up = Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. б), катетами которого являются активное Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени. Из треугольника сопротивлений следует: 41.2. Полное сопротивление. Полное сопротивление (Z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного. 41.3. Угол сдвига фаз между напряжением и током. Аргумент комплексного сопротивления j есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как j = arctg(X/R). Следовательно, сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи. Из выражения 41.4. Закон Ома для действующих и амплитудных значений тока и напряжения. В активном элементе r происходит необратимое преобразование электрической энергии в тепловую энергию. Мгновенные значения тока i и напряжения u связаны законом Ома: Если ток изменяется по синусоидальному закону 42. Энергетический процесс. Мгновенная, активная, реактивная и полная мощности. Треугольник мощностей. Коэффициент мощности. Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепиПо определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем: Для единичного заряда на участке A-B: Для всех зарядов: Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности: мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке: Если участок цепи содержит резистор c электрическим сопротивлением R, то Активная мощностьИзмеряется в W [Вт] Ватт.Среднее за период T значение мгновенной мощности называется активной мощностью: Реактивная мощность Единица измерения — вольт-ампер реактивный (var, вар) Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду. Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными. Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике. Полная мощность Единица полной электрической мощности — вольт-ампер (V·A, В·А) Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели,распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах. ТРЕУГОЛЬНИК МОЩНОСТЕЙ - графическое изображение активной, реактивной и полной мощностей в цепи переменного тока. Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения. Численно коэффициент мощности равен косинусу этого фазового сдвига. Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы: 1. 2. 3. 4. Здесь 43.1. Последовательное соединение активного, индуктивного и ёмкостного сопротивлений При последовательном соединении активного r , индуктивного xL и ёмкостного xC сопротивлений (рис.8 а) мгновенное значение напряжения источника согласно второму закону Кирхгофа определяется алгебраической суммой мгновенных значений напряжений на отдельных элементах: Если все эти напряжения представить в виде векторов на векторной диаграмме, то действующее значение напряжения источника определяется, как векторная сумма действующих значений напряжений на отдельных элементах и может быть рассчитано по формуле: Учитывая, что по закону Ома Тогда где: Полное сопротивление цепи Z , активное r и реактивное треугольник сопротивлений , для которого справедливы следующие соотношения: 43.2. II закон Кирхгофа для мгновенных значений. Второй закон Кирхгофа Рассмотрим контур, выделенный из сложной цепи переменного тока Запишем второй закон Кирхгофа для мгновенных значений: Все мгновенные значения изобразим в виде комплексов, опустим знак мнимой части, сократим на В контуре цепи синусоидального тока алгебраическая сумма комплексов ЭДС равна алгебраической сумме комплексов падений напряжений. 43.3.Временная и векторная диаграммы для различного характера цепи. 1) 2) 3) Читайте также: lektsia.com Электричество и автоматизация. Мощность через закон ома
Закон Ома для чайников
Выводы из закона Ома

Расчеты с применением больших и малых величин
Мощность и закон Ома
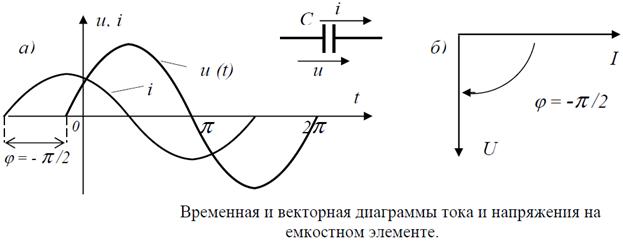
Закон Ома для действующих и амплитудных значений тока и напряжения.
⇐ ПредыдущаяСтр 7 из 10Следующая ⇒



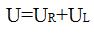
 по направлению совпадает с вектором тока I, а вектор
по направлению совпадает с вектором тока I, а вектор  направлен перпендикулярно вектору I с положительным углом.
направлен перпендикулярно вектору I с положительным углом. >0, но <
>0, но <  , а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения вактивном и индуктивном сопротивлениях
, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения вактивном и индуктивном сопротивлениях  и
и  :
:  =Ucos
=Ucos 



 и индуктивное
и индуктивное  сопротивления, а гипотенузой – величина
сопротивления, а гипотенузой – величина  .
.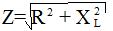
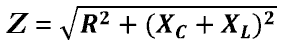 - полное сопротивление цепи.
- полное сопротивление цепи. следует, что положительные значения j соответствуют отставанию тока по фазе, а отрицательные - опережению.
следует, что положительные значения j соответствуют отставанию тока по фазе, а отрицательные - опережению.
 тогда напряжение:
тогда напряжение: С другой стороны мгновенное значение напряжения:
С другой стороны мгновенное значение напряжения: Отсюда получен закон Ома для амплитудных значений:
Отсюда получен закон Ома для амплитудных значений:  , и закон Ома для действующих значений:
, и закон Ома для действующих значений: 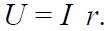
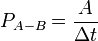


 по определению, в результате получаем:
по определению, в результате получаем: 
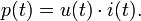

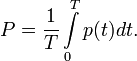 В цепях однофазного синусоидального тока
В цепях однофазного синусоидального тока  где U иI — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле
где U иI — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле  В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением 
 (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Рсоотношением:
(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Рсоотношением:  .
. где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).
где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).
 Треугольник мощностей получается из соотношения Р2 + Q2 = S2.
Треугольник мощностей получается из соотношения Р2 + Q2 = S2.



 — активная мощность,
— активная мощность,  — полная мощность,
— полная мощность,  — реактивная мощность.
— реактивная мощность.



 ,
,  - закон Ома ,
- закон Ома , - полное сопротивление цепи при последовательном соединении элементов.
- полное сопротивление цепи при последовательном соединении элементов. образуют
образуют


 .
. и разделим на
и разделим на  (по аналогии с законом Ома):
(по аналогии с законом Ома):
 .
.


Электротехника. Основы. Закон Ома - Всё об энергетике
Электротехника. Основы. Закон Ома
В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.
Закон Ома
Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.
Закон Ома для участка цепи без ЭДС
Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:
\begin{equation} I = {U_{ab}\over R}; \end{equation}Где:
- I - ток через участок ab электрической цепи;
- Uab - напряжение на участке ab электрической цепи;
- R - сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = U_{ab} × G; \end{equation}Где:
- G - проводимость участка ab электрической цепи.
Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

Рисунок 1 - Участок цепи без ЭДС
Закон Ома для участка цепи содержащего ЭДС
Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {U_{ab} + E\over R}; \end{equation}Где:
- I - ток через участок ac электрической цепи;
- Uab - напряжение на участке ab электрической цепи;
- E - ЭДС на участке bс электрической цепи;
- R - сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}Где:
- G - проводимость участка ab электрической цепи.
Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

Рисунок 2 - Участок цепи содержащий ЭДС
Закон Ома для полной цепи
Закон формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {E\over {R + r}}; \end{equation}Где:
- I - ток в электрической цепи;
- E - ЭДС электрической цепи;
- R - сопротивление электрической цепи;
- r - внутреннее сопротивление источника ЭДС.
Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

Рисунок 3 - Полная цепь
На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на Rп
\begin{equation} I = {E\over R_п}; \end{equation}Где:
- Rп - полное сопротивление электрической цепи (включая сопротивление источника ЭДС).
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].
\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}Где:
- \(\vec\jmath\) - плотность тока;
- ρ - удельное сопротивление;
- \(\vec E\) - напряжённость электрического поля.
Примеры применения
Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.
Пример 1
Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

Рисунок 4 - Схема к 1 и 2-му примеру
Для решения задания воспользуемся выражением (1):
\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}Пример 2
Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.
Для решения задания преобразуем выражение (2) относительно G:
\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}Пример 3
Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

Рисунок 5 - Схема к 3-му примеру
Для решения задания преобразуем выражение (3) относительно E:
\begin{equation} I = {U - E\over R} \ \Rightarrow \ {I × R} = {U - E} \ \Rightarrow \ E = {U - I × R}; \end{equation}Подставим в выражение (10) известные величины:
\begin{equation} E = {U - I × R} = {220 - 0,5 × 140} = {150 \ В;} \end{equation}
Пример 4
Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь - 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.
Преобразуем выражение (5) относительно r:
\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E - I × R} \ \Rightarrow \ r = {E - I × R\over I}; \end{equation}Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:
\begin{equation} r = {E - I × R\over I} = {9 - 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}
Использованные термины
Электрический потенциал точки:
Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.
Электрическое напряжение:
Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: Uab = φa - φb.Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение - скалярная величина, но на электрических схемах указывают его положительное направление.
Электродвижущая сила (ЭДС):
Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС - скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.
Электрическое ток:
Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление - направленное движение заряженных частиц.Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].
Плотность тока:
Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м2). Плотность тока - векторная величина [4].
Электрическое сопротивление:
Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление - скалярная величина.
Электрическая проводимость:
Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость - скалярная величина.
Удельное сопротивление:
Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2.Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].
В дальнейшем при использовании вышеперечисленных терминов слово "электрический" будет упускаться.
Список использованных источников
- Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов - Москва: Высшая школа, 1996. - 623 с.
- Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. - 318 с.
- Википедия - Удельное электрическое сопротивление [электронный ресурс] - Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
- Википедия - Плотность тока [электронный ресурс] - Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока
allofenergy.ru
ЗАКОН ОМА
На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов: источника напряжения — батареи GB, потребителя тока — нагрузки R, которой может быть, например, нить накала электрической лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Между прочим, если эту цепь дополнить выключателем, то получится полная схема карманного электрического фонаря.

Нагрузка R, обладающая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:
I = U/R
где I — ток, выраженный в амперах, А; U — напряжение в вольтах, В; R — сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома.
Первый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи.Решение: I = U/R = 25 / 5 = 5 А.Второй пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.Третий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Следовательно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.В связи с этим приведу еще один пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.Закон Ома и производные от него расчетные формулы, достаточно легко запомнить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:

>Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.
Теперь рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом, как это показано на рис...

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом — сопротивление нити лампочки Н плюс 25 Ом — сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, т.е. почти такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи. Можно включать амперметр в любую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.Добавочный резистор, включаемый в цепь последовательно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, Здесь U — падение напряжения, В; I — ток в цепи, A; R — сопротивление добавочного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где R — искомое сопротивление добавочного резистора, Ом; U-напряжение, которое необходимо погасить, В; I — ток в цепи, А. Для нашего примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, и таким образом регулировать ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, однако, и другой способ подключения нагрузки к источнику тока с избыточным напряжением — тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис...

Здесь R1 — резистор, включенный потенциометром, a R2 — нагрузка, которой может быть та же лампочка накаливания или какой — то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет). По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 — лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех Случаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком — то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.
Спасибо lessonradio.narod.ruwww.radioingener.ru
Закон ома
Соотношение между значениями тока, ЭДС и сопротивления в электрической цепи носит название закона Ома. В девятнадцатом веке Георг Ом вывел математические соотношения между основными характеристиками электрической цепи. Закон Ома говорит: чем больше напряжение, тем больше ток, и чем больше сопротивление, тем меньше ток. Математически этот закон представляется так: ток в цепи прямо пропорционален ЭДС и обратно пропорционален сопротивлению цепи.

В любой из грех приведенных формул при двух известных параметрах электрической цепи оставшийся неизвестным параметр может быть рассчитан. Закон Ома неприменим к цепям переменного тока, поскольку витки проводов вызывают различные эффекты при таком токе. Переменный ток будет обсуждаться в последующих главах. Тем не менее общие понятия закона Ома справедливы для цепей переменного тока.
Закон Ома делает возможным расчет значения недостающего множителя, если значения двух других известны или могут быть измерены. На 1.10 представлен простой способ запоминания закона Ома. Если в круге заштрихован один из множителей, остальные буквенные обозначения в круге дадут правильную формулу для расчета заштрихованного множителя.
Условные обозначения в этих формулах те же, что и в выражениях для закона Ома; при этом Р символизирует мощность в ваттах. Следующие три примера иллюстрируют расчет мощности для трех электрических цепей.
Все вокруг нас — твердые тела, жидкости и газы — состоит из материи. Материя может быть разбита на молекулы (мельчайшие частицы физических объектов) и атомы (мельчайшие частицы элемента, которые могут встречаться отдельно или в сочетании с другими атомами). Атом состоит из ядра (центральной части) и электронов (отрицательно заряженных), которые вращаются вокруг ядра наподобие планет, вращающихся вокруг солнца. Ядро состоит из протонов (положительно заряженных) и нейтронов (не имеющих заряда). Количество протонов, как правило, равно количеству электронов, что делает атом электрически нейтральным. При потере электрона атом становится положительно заряженным, а при захвате — отрицательно заряженным. Закон электрических зарядов утверждает, что одноименные заряды отталкиваются, а разноименные — притягиваются. Можно получить материалы с положительным или отрицательным зарядами.
Электроны могут приводиться в движение с помощью трения, химических реакций и магнетизма. Проводник — это материал, способный пропускать электроны и электричество. Большинство металлов являются проводниками. Изолятор — материал, который противодействует движению электронов или предотвращает его.
Существуют четыре важных параметра в любой электрической цепи: электродвижущая сила, ток, сопротивление и мощность. Электродвижущая сила цепи — это фактически действующее электрическое давление в ней, наподобие водяного давления в гидравлических системах. Электродвижущая сила электрической цепи измеряется в вольтах. Напряжение давления должно быть достаточным для преодоления сопротивления цепи. Переменный ток в промышленности используется исключительно для питания оборудования электроэнергией.
Количество электронов, протекающих в электрической цепи, называется электрическим током. Ток в электрической цепи измеряется в амперах. Ампер — это количество тока, которое проходит через сопротивление один Ом при напряжении один вольт.
Сопротивление электрической цепи измеряется в омах. Любая электрическая нагрузка имеет какое-нибудь сопротивление. Мощность — скорость потребления энергии электрической цепью. Мощность измеряется в ваттах и киловаттах. Поставщики электроэнергии в большинстве случаев пользуются киловатт-часами для расчетов с потребителями электричества. Киловатт-час — это мера электрической энергии, учитывающая продолжительность потребления энергии и ее мощность. Одна тысяча ватт, использованная за период времени один час, равнозначна одному киловатт-часу. Вольты, амперы, омы и ватты часто используются совместно с приставками кило- или милли-, чтобы представить большие или меньшие количества этих величин и избежать использования чрезвычайно больших или малых чисел.
Закон Ома дает соотношение между значениями тока, электродвижущей силы и сопротивлением электрической цепи. Это соотношение представляется в математической форме. Когда любые два параметра электрической цепи известны или могут измеряться, можно воспользоваться формулой закона Ома для нахождения третьего параметра. Мощность может рассчитываться с помощью выражения Р = 1-Е.
blockstroi.ru
Закон Ома для полной цепи
Что такое ЭДС, мы с вами говорили еще в этой статье. Помню как-то на уроке физики в 8 классе препод спросил:
— Что написано на пальчиковой батарейке?
— Напряжение батарейки, — хором ответили мы.
— Побрейтесь! Это ЭДС!
— !?
— На батарейках указано именно ЭДС!
После этих гордых слов препод начал урок. Он ставил какие-то опыты, зажигал лампочки, писал что-то на доске… Но я все равно ничего не догнал, потому что весь урок играл с товарищем по парте в морской бой ;-). Только спустя годы, прочитав советский словарь радиолюбителя, наконец-то понял, что ничего сложного в этом нету. И если закон Ома для участка цепи знают почти все, то сложности возникают именно по закону Ома для полной цепи. Но оказывается, все до боли просто!
Итак, знакомьтесь, автомобильный аккумулятор! Не исключено, что вы когда-нибудь его видели вживую))
Для дальнейшего его использования, припаяем к нему два проводочка: красный на плюс, черный на минус
Наш акум готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
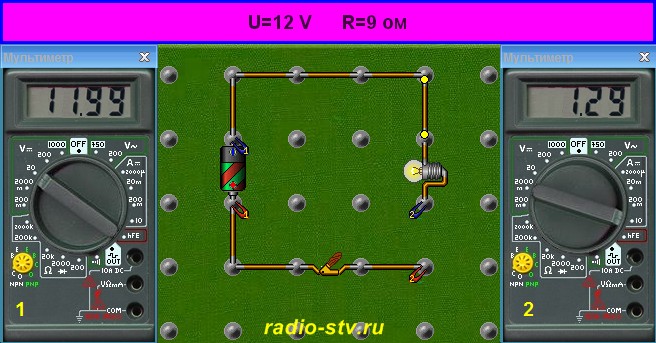
Первым делом давайте замеряем напряжение на клеммах акума
12,09 Вольт. Вполне нормально, так как наш акум выдает именно 12 Вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС нашего акума.
Подключаем галогенку к акуму и снова замерям напряжение:
Видели да? Напряжение на акуме просело до 11, 79 Вольт!
А давайте по приколу замеряем, сколько кушает наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр у нас будет замерять силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер, напряжение просело до 11,79 Вольт.
Давайте вместо галогенки поставим простую лампочку накаливания от поворотника
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на акуме. Вместо акума может быть простая батарейка полутора Вольт или какая-нибудь другая батарейка или аккумулятор. Суть от этого не меняется.
Ну а теперь немного нудной теории)).
Источник ЭДС на схеме выглядит вот так:

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток, а точнее напряжение. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогеновых ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем акуме был идеальный источник ЭДС, тогда бы напряжение на клеммах акума никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока жрет нагрузка. Что-то здесь не так. Но почему так происходит? Этот вопрос задавал себе и немецкий физик Георг Ом и все-таки наконец-то он нашел объяснение этому процессу.
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС акума. И оно называется внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r«. Выглядит все это в акуме примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Итак, что имеем? Идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения . Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом резисторе.
Это означает, что на каждом сопротивлении падает какое-то напряжение:
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur.
Теперь вспоминаем статью Делитель тока. Кто не помнит, напомню. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Последнее выражение носит название закона Ома для полной цепи. Из этого выражения мы можем найти внутреннее сопротивление акума r.
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы цепанули нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:


Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы. Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень жестко просядет напряжение. Это можно увидеть, если замкнуть клеммы акума толстым медным проводом и замерять в это время напряжение на клеммах)). Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник напряжения. Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осцилл имеют ну очень большое сопротивление между своими щупами.
www.ruselectronic.com
Закон Ома для полной цепи (DC)
Электротехника: Основы
Закон Ома для полной цепи (DC)
Рассмотрим Закон Ома (Ohm's law) для полной электрической цепи постоянного тока. Здесь нас прежде всего интересует его практическое отношение к постоянному току (direct current). Различают две формулировки Закона Ома, одна для участка цепи, а другая для полной цепи. В последней учитывается источник тока, точнее его внутреннее сопротивление.
Простейшая электрическая цепь постоянного тока состоит из источника тока и одной единственной резистивной нагрузки, а попросту из — активного сопротивления.

Закон Ома — закон пропорциональности
Формулировка Закона Ома для полной цепи и для участка цепи — это утверждение пропорциональности. Устанавливается достаточна простая алгебраическая связь между величинами силы тока, суммы сопротивлений (r+R) и ЭДС источника тока.
Сила тока в электрической цепи, прямо пропорциональна ЭДС источника и обратно пропорциональна сумме внутреннего сопротивления этого источника и общего сопротивления цепи.
Наиболее понятное и простое применение Закона Ома в такой формулировке — это электрическая цепь с одним источником тока в ветви (контуре). Кроме Закона Ома, для расчёта электрических цепей, необходимо знать правила Кирхгофа, а также иметь базовые представления об элементах цепей, таких как узлы, ветви, контуры, двухполюсники и т. п. Но ограничившись только Законом Ома для полной цепи можно сделать несколько важных выводов.
Потери на внутреннем сопротивлении источника ЭДС
Самый простой пример иллюстрирующий влияние внутреннего сопротивления источника тока — это гальванические элементы (батареи) и аккумуляторы. Способность источника тока выдавать большое значение силы тока напрямую зависит от его внутреннего сопротивления. Чем оно больше, тем меньший ток способен выдать источник ЭДС.
Допустим у нас имеется аккумуляторная батарея на 12 Вольт (В), а в качестве нагрузки мы применяем лампу накаливания мощностью 24 Ватт (Вт). Как узнать сопротивление нагрузки при устоявшемся режиме работы, то есть когда лампа горит в полный накал? Это сделать достаточно просто. Мощность (24 Вт) делим на напряжение (12 В), в итоге мы получаем расчётное значение рабочего тока в 2 Ампер (А).
Чтобы вычислить сопротивление нагрузки, нужно воспользоваться Законом Ома для участка цепи. В нашем случае падение напряжения на нагрузке, то есть лампе накаливания должно быть 12 В, а рабочий ток для выхода на мощность в 24 Вт будет 2 А. Применяем закон пропорциональности и находим сопротивление нагрузки.

В итоге мы получаем расчётное рабочее сопротивление нагрузки R равное 6 Ом (12 В/2 А).
Теперь же вернёмся к нашему источнику ЭДС с его внутренним сопротивлением. Как оно будет влиять на ток в цепи? Допустим, что мы измерили напряжение на клеммах аккумулятора и оно оказалось равным 12,5 Вольт, затем подключили нашу нагрузку — лампочку накаливания 24 Ватт, на номинальное напряжение в 12 Вольт. Вроде бы всё должно работать, но оказывается, что лампа светит тускло, в половину накала. В чём же может быть причина? Вот тут как раз таки можно и нужно применять Закон Ома для полной цепи. Необходимо учитывать внутреннее сопротивление источника. Так как визуально лампа светит тускло, значит не выходит на свою норму в потребления 24 Вт, а значит напряжение и ток на ней недостаточны. Казалось бы, подключили к аккумулятору у которого на выходе 12,5 Вольт, но что-то тут не так. Что именно?
Нужно провести измерение падения напряжения непосредственно на лампе, тогда окажется, что оно совсем не 12 Вольт, а гораздо меньше, допустим 6 Вольт. Условно предположим, что сопротивление лампы в 6 Ом стабильно и не зависит от нагрева. Тогда мы можем вновь воспользоваться Законом Ома для участка цепи, чтобы найти значение тока. В нашем случае это достаточно просто сделать. Необходимо падение напряжения на лампе в 6 Вольт, разделить на её сопротивление в 6 Ом. В результате мы получим значение тока в цепи равное 1 Ампер. Вот оно что! Для того, чтобы лампа горела как положено и давала все свои 24 Ватт мощности, нужен ток в 2 А, а у нас ровно половина — 1 А. Можно сразу сказать, что на лампе выделяется мощность всего в 6 Ватт, что явно недостаточно.
Почему же при ЭДС источника — аккумулятора в 12,5 Вольт происходит такое, казалось бы несоответствие? Сумма падений напряжений в контуре, а у нас как раз таки один единственный контур цепи, всегда равно ЭДС источника. Отсюда делаем вывод, что у нас куда-то делось 6,5 Вольт (12,5-6). А делись они вот куда. Внутреннее сопротивление источника тока можно выделить наружу только в схеме, а на практике оно как бы глубоко запрятано в конструкции источника. Разумеется, что разобрав источник на части, мы не обнаружим там никакого внутреннего сопротивления. Оно существует умозрительно, на схемах, для удобства, а в реальности это характеристика сторонних сил, которые создают ту самую ЭДС.
В итоге, у нас выходит, по вышеприведённому примеру, что сам источник тока съедает мощность на себя, да ещё к тому же она больше, чем полезная нагрузка — лампочка. При токе в 1 А, и при падении напряжения в 6,5 В на внутреннем сопротивлении мы имеем 6,5 Вт бесполезных потерь на источнике тока!!! Выдаёт на нагрузку 6 Вт, а сам кушает чуть больше — 6,5 Вт. Эффективность заведомо меньше 50%. Вот вам и применение Закона Ома для полной цепи.
Давайте попробуем решить обратную задачу. Какое внутреннее сопротивление источника тока с ЭДС равной 12,5 Вольт должно быть, чтобы падение напряжения на лампе в 24 Вт было равным 12 В?
Исходя из задачи, можно сразу же вычислить падение напряжения на внутреннем сопротивлении. Оно должно быть в нашем случае равным всего 0,5 В. Но для того, чтобы пользуясь Законом Ома вычислить значение внутреннего сопротивления, нам нужно знать силу тока. Учитывая, что мы хотим получить с нагрузки 24 Вт мощности, то для этого нам необходим ток в 2 Ампер. Для расчёта можно смело брать эту величину. Теперь узнать внутреннее сопротивление источника достаточно просто. Оно будет равно 0,5 В делённые на ток в 2 А, то есть 0,25 Ом. Эта величина значительно меньше той, которая была в примере, когда лампа горела тускло, всего на 6 Вт мощности.
При внутреннем сопротивлении в 0,25 Ом и при нагрузке в 6 Ом мы получим достаточно эффективное использование источника тока. На нагрузке у нас будет выделятся мощность в 24 Вт, а потери источника на внутреннем сопротивлении составят всего на всего 1 Вт (0,5Х2). Соотношение меньше чем 1 к 10. Однако, если мы с вами к источнику с таким малым внутренним сопротивлением подключим нагрузку в 0,25 Ом, то есть внутреннее сопротивление и сопротивление нагрузки равны, тогда ток в цепи подскочит до значения 25 А (12,5/0,5). На нагрузке будет выделятся мощность равная 156,25 Вт и точно такая же будет расходоваться в самом источнике.
Выбор источника тока по мощности нагрузки
Правильное понимание Закона Ома для полной цепи позволяет правильно рассчитать и выбрать источник тока по нагрузке, а также позволяет своевременно выявить дефекты источников тока. Тот источник тока, который не пригоден для низкоомной нагрузки, потому как его внутреннее сопротивление в больше или равно сопротивлению нагрузки, будет вполне пригоден в эксплуатации для питания электрической цепи с нагрузкой в 10 раз большим сопротивлением, чем его собственное.
Чем большую мощность нужно получить на нагрузке при малом значении ЭДС, тем меньше должно быть внутреннее сопротивление источника. Поэтому самыми лучшими источниками постоянного тока (DC) в настоящее время остаются химические аккумуляторы, хотя вполне возможно, что их могут превзойти в этом полупроводниковые источники тока — солнечные батареи.
Оптимальным считается, когда падение напряжения на внутреннем сопротивлении, более чем в 10 раз меньше чем падение напряжения на полезной нагрузке. Если говорить языком пропорциональности, то это означает, что зная сопротивление нагрузки или её мощность, нужно выбирать источник тока, где его внутреннее сопротивление (импеданс) будет более чем в 10 раз меньшим.
Дата: 18.05.2015
© Valentin Grigoryev (Валентин Григорьев)
Тег статьи: Закон Ома
Все теги раздела Электротехника:Электричество Закон Ома Электрический ток Электробезопасность Устройства Биоэлектричество Характеристики Физические величины Электролиз Электрические схемы Асинхронные двигатели
www.electricity-automation.com






.jpg)





Поделиться с друзьями: