Регулирование скорости изменением числа пар полюсов стало возможным из-за секционной конструкции статора асинхронного двигателя с короткозамкнутым ротором. На практике выпускаются 2-х, 3-х, 4-х скоростные асинхронные двигатели, где число пар полюсов всегда кратно целому числу, вследствие чего, данный способ обеспечивает только ступенчатое регулирования скорости, а двигатели получили название многоскоростные. На деле существует большое количество схем включения обмоток статора, но наиболее часто используемые: - переключение обмотки треугольник-двойная звезда;
- переключение обмотки звезда-двойная звезда. Треугольник-двойная звезда Рисунок 1 – Схема переключения треугольник-двойная звезда Рисунок 2 – Механическая характеристика при переключение с треугольника на двойную звезду А - треугольник;
Б - двойная звезда. Данный тип регулирования скорости, в частных случаях осуществляет переключение скорости с некоторой временной рекуперацией энергии. Этот способ переключения занял нишу в грузоподъемных механизмах. Вы можете видеть, что при увеличении числа пар полюсов, скорость падает вдвое, но критический момент возрастает тоже в два раза, что дает нам возможность осуществлять подъем, но с более медленной скоростью. Называют такое условие работы – «тяговый» режим. Сравнивая мощности, видно, что мощность изменяется незначительно, а скорость ступенчатым образом изменяется вдвое. Рассматривая подробнее механическую характеристику при таком переключении, мы можем заметить, что работая в точке 1, кривая А, при включении на схему двойная звезда, асинхронный двигатель перейдет в точку 2 кривая Б, и начнет происходить рекуперативное торможение, до того момента, пока двигатель не перейдет в двигательный режим, а далее в точку работы 3 кривая Б. Данное торможение возможно, когда скорость вращения ротора асинхронного двигателя больше чем синхронная скорость. Частным примером такой работы мы рассмотрели в предыдущей статье про торможение противовключением, в которой рассказывалось как производят спуск груза в грузоподъемных механизмах с отдачей энергии в сеть. Звезда-двойная звезда Рисунок 3 – Схема переключения звезда-двойная звезда Рисунок 4 – Механическая характеристика при переключение со звезды на двойную звезду
А - звезда;
Б - двойная звезда. На рисунке выше видно, что критическим момент остается прежним, а синхронная скорость уменьшается вдвое. Говоря про мощность, то при переключении на двойную звезду, она возрастает вдвое. При переключении обмоток, работая в точке 1 кривая А, перейдем в точку 2 кривая Б, и с точки 2 в точку 3, так же как и в предыдущем случае будет осуществляться рекуперативное торможение. h4e.ru В выпрямителях применяются трансформаторы специального назначения, так как эти источники тока имеют такие характерные особенности, как неодновременная нагрузка различных фаз в соответствии с неодновременным прохождением тока через вентили блока выпрямителей. Как правило, обмотки трехфазных трансформаторов соединяют следующим образом звезда — две обратные звезды с уравнительным реактором звезда — звезда звезда—двойной зигзаг треугольник — звезда. К. п. д. трансформаторов источников тока для электрохимической обработки обычно несколько меньше, а масса несколько больше, чем трансформаторов обычного типа. [c.177] Рассмотрим сперва динамику двойной звезды, взяв в качестве примера систему 70 в созвездии Змееносца. Приняв одну из двух звезд непод-ВИ.ЖНОЙ, орбиту второй можно изобразить в виде эллипса, пробегаемого Рис. 25. Истинные абсолютные ор- за 89 лет большую полуось его обо-биты компонентов двойной звезды значим через а, а малую — через Ь. [c.60] Итак, для устойчивости двойной звезды надо, чтобы правая часть равенства была отрицательной, т. е. потенциальная энергия должна превы- [c.60] При переходе от двойной звезды к тройной проблема усложняется могут быть случаи устойчивых систем (рис. 26), где одна из звезд движется вокруг двух других по эллипсу, находясь при этом далеко от них, т. е. мало возмущая их движение. Могут быть и случаи неустойчивости при взаимных расстояниях трех компонент. Рис. 26. Конфигурации типа I тронной системы близких по величине од- тройной системы (б) [c.61] Так, Ж. П. Аносова решила 200 задач по движению трех звезд одинаковых масс, тип начального расположения которых представлен на рис. 26 при этом были приняты меры к тому, чтобы вся совокупность начальных условий не содержала банальных повторений, была представительной совокупностью, отобранной из бесконечного множества возможных систем. При этом принято было добавочное условие отсутствия вращения системы в целом, что существенно для дальнейших рассуждений. Во всех случаях решались уравнения движения, определялись траектории звезд, положение их в определенные моменты времени и скорости. Решение задачи рано или поздно приводило к распаду тройной системы с выбрасыванием одной из трех звезд и стабилизацией оставшейся двойной звезды. Избыточная кинетическая энергия уносилась третьей звездой. [c.61] Разработан также метод формования полиэфирных волокон из профилированных фильер, имеющих форму звезд с несколькими лучами (>2, обычно из 5 лучей). Лучи фильер состоят из тонких щелей 0,05—0,08 мм ширины и примерно двойной длины. Волокна, сформованные из этих фильер, имеют сечение в виде пятиконечной звезды, которое сохраняется после вытягивания волокон на холоду или при нагревании. Такое сечение волокон предотвращает скольжение и сползание нитей в трикотажных изделиях и тканях [1829]. [c.114] Интересно, что даже и после того как иррегулярные силы установят максвелловское распределение скоростей, полная строгая стационарность системы оказывается все еще не достигнутой. Вычисления показали, что около 0,007 от общего числа звезд системы должно иметь при максвелловском распределении скорость больше критической, так что такие звезды могут покидать Галактику. На это способны каждые 7 звезд из тысячи. Происходит диссипация, т. е. постепенное рассеяние системы. Как только эти семь звезд уйдут, максвелловское распределение нарушится и иррегулярные силы восстановят содержание быстрых звезд, которые через некоторое время также уйдут из Галактики. Процесс диссипации будет происходить медленно, но верно, пока от звездной системы останется двойная звезда с ее замкнутыми орбитами и невозможностью дальнейшего распада без внешнего воздействия. [c.66] В одинарных прямоугольных рамках —состояния звезд, в овальных рамках —видимые явле [ия, в двойных прямоугольных рамках—явления, непосредственно связанные с синтезом элементов. [c.21] Вернемся к системам в которых не образуются двойные соли. Если провести сечения пространства диаграммы изотермическими поверхностями, то в точке инверсии получится звезда, в которой сходятся четыре ноля отдельных солей и четыре пограничные линии, отвечающие равновесию раствора с двумя солями. Выше и ниже этой точки на изотермических сечениях будем иметь по две звезды, в которых сходятся по три поля и по три пограничные кривые. Более детальное рассмотрение строения диаграмм взаимных водных систем дано ниже. [c.344] Напомним еще об одном термине, с которым мы уже встречались,— это звезды . Звездой называется совокупность элементов, имеющих одну общую точку,— ее вершину. Например, три поля кристаллизации вместе с тремя пограничными кривыми, по которым они попарно пересекаются, и с принадлежащей им тройной эвтектической точкой как раз образуют звезду, причем вершиной ее будет указанная эвтектическая точка. Размерность равна размерности полей для двойной системы этой звезды. Можно мыслить себе звезды более высокой и более низкой размерности. Так, совокупность нескольких линий, пересекающихся в одной точке, образует одномерную звезду. Совокупность четырех объемов кристаллизации вместе с шестью разграничивающими их поверхностями вторичных выделений, четырьмя соответствующими линиями третичных выделений и четверной эвтектикой образует трехмерную звезду, причем эвтектика будет ее вершиной — нульмерная звезда — это просто точка. Звезда — комплекс незамкнутый, так как в нее не входят элементы, отделяющие объемы, плоскости и линии диаграммы от пространства, в котором они находятся. Принимаются во внимание только элементы, сходящиеся в вершине. Как и о фазовом комплексе, о звезде говорят, что она взаимна данному комплексу. [c.459] Переменные звезды делятся на три, основных. класса пульсирующие, эруптивные и затменно-двойные. [c.981] Затменно-двойные звезды [18]. Обозначение Е. На 1958 г. зарегистрировано 2763 объекта. Двойные системы с плоскостью орбиты, близкой к лучу зрения наблюдателя. При вращении вокруг общего центра тяжести один компонент затмевает другой. Периоды изменения блеска совпадают с периодами обращения по орбите (от нескольких часов до десятков лет). Амплитуда изменения блеска может достигать нескольких звездных величин. [c.983] Для измерения выбирают как одиночные следы, так и звезды , состоящие из двойных и тройных треков. Измерение производят с возможно большей точностью. Определяют пробег а-частиц в эмульсии, находят их энергию, а по энергии определяют радиоактивный элемент, подвергшийся распаду. Звезды представлены на рис. 35. [c.112] Двойные треки ( звезды ) [c.113] Подшипники качения защищены двойным торцовым уплотнением. Типоразмеры О, А и В включают по схеме звезда — треугольник. [c.264] На второй вопрос не может быть более убедительного ответа, чем ссылка на хорошо известный результат астрономических наблюдений. Известно потускнение двойных звезд, которые состоят из яркой звезды и более темного спутника. Так как эти звезды могут быть удалены на расстояние в сотни световых лет, то при заметных изменениях скорости света с длиной волны наблюдались бы заметные цветовые изменения. Однако ничего подобного не отмечалось. [c.102] Общие закономерности космич. распространенности Э. X. в природе представлены на графике Зюсса и Юри (рис.). Наиболее распространены в космосе водород и гелий (на Земле их распространенность мала по причине летучести). В основном распространенность Э. X. в космосе уменьшается с ростом ат. веса, но обнаруживает резкий максимум в группе железа ( железный пик ) и двойные максимумы вблизи магических чисел нейтронов 50, 82, 126, к-рые отвечают заполненным ядерным оболочкам. Легкие Э. х., Li, Be, В, лежат гораздо ниже основной кривой, что объясняется разрушением их ядер (выгоранием) при термоядерных реакциях в недрах звезд. Выше основной кривой лежат Э. х., ядра к-рых могут быть построены из целого числа а-частиц (ядер гелия) — С, О, Ne, Mg, Si, S, Ar, a, или участвуют в углеродном цикле ядерных реакций в звездах — С, N, О. Все эти закономерности ядерная астрофизика объясняет образованием элемеитов посредством ядерных реакций в недрах звезд и ири звездных взрывах (вспышках Сверхновых). Основные ядерные процессы, помеченные на рисунке гелиевые реакции (а) медленный (s) и быстрый (г) захват нейтронов образование Э. X. группы железа в условиях, близких к [c.497] Участки кривой А соответствуют соединению вторичной обмотки трансформатора двойной звездой или трехфазному соединению зв дой с отводом от нулевой точки участки кривой Б соответствуют соединению вторичной обмотки трехфазным мостиком. Технические характеристики некоторых селеновых вентилей сведены в табл. 2-8. [c.69] На треугольнике для таких систем линии двойных эвтектик образуют две трехлучевые эвтектические звезды с центрами El и Е2- Допустим, что вещество А вступает в соединение с веществом С, причем образуется соединение А, С . Этому соединению на линии состава АС отвечает точка D (рис. 43). Соединив эту точку с вершиной треугольника В, получим линию BD, которая делит треугольник AB на два других треугольника— ABD и DB. [c.145] Если бы представить звезду такой же средней плотности, как у солнца, но в 50 раз его превосходящую по массе, то для того, чтобы вырваться из сферы притяжения такого светила, тело или частицы должны были бы обладать огромною скоростью около 2 240 ООО м в секунду. Но такие звезды, в 50 раз по массе превосходящие наше солнце, едва ли не составляют крайний предел массы светил, потому что многочисленные наблюдения над собственными движениями двойных звезд показывают, что масса большинства их или меньше солнечной, или превосходит ее лишь в небольшое число раз, и только наш известный астроном Белопольский (1898) для т Viгgiпis определил общую массу в 32.7 раза превос.ходящую солнце. А так как яркость обеих звезд (двойной звезды) одинакова, то можно думать, что нет отдельных звезд, превосходящих солнце даже в 30 раз, а тем более в 50 раз. Поэтому можно полагать, что V для частиц эфира недалека (но не меньше) 2 000000 м в секунду, а отсюда, если эфир считать элементарным газом, сходным с аргоном, его атомный вес (принимая Н= 1) л недалек от 0.000001. Указанным путем, хотя и чисто гипотетически, объясняются некоторые качества мирового эфира, особенно же его везде присутствие, все проникание и невозможность опытного его уединения. Можно при этом предполагать, что среда мирового эфира, как наша атмосфера, содержит не один, а разные газы в смеси, но такая и вся вышеизложенная гипотеза еще доныне не вызываются с настоятельною потребностью и приведены мною здесь лишь для того, чтобы показать возможность понемногу освещать с реальной точки зрения те громадные области неизвестного, которые предстоит так или иначе если не постичь, то помирить о окружающими нас явлениями и принимаемыми предположениями, не создавая каждый раз совершенно новых понятий, подобных, например, представлению об эфире, как материи совершенно невесомой, но упругой. На мой личный взгляд (а в свободном деле научного миросозерцания ничего иного и нет, кроме более или менее личных взглядов, потому что нет сдерживающего руководительства опытом), все познается сознанием, т. е. духовно и только в этом смысле может быть речь об единстве, помимо же того дух, движение (энергия) и вещество (материя) сколько-либо постигаются только не сливаемые, в отдельности, как время и пространство. Когда идет речь о веществе — первее всего рождаются вопросы о его весомости и химической природе, и вышеизложенные соображения о веществе мирового эфира назначаются только для предположительного ответа на указанные вопросы. Такой путь мне представляется согласным со всею историею реальных знаний. Подробнее об этом предмете я говорю в брошюре Попытка химического понимания мирового эфира , напечатанной в 1905 г. [c.149] На рис. 229—231 приведены диаграммы плавкости систем со звездами двойного, тройного и четверного подъема. Для фазовых комплексов этого типа, изображенных отде.тьно, рядом с диаграммами плавкости, характерно наличие вершин , обращенных к одной из вершин тетраэдра. Для сплавов систем этого типа характерно повышение растворимости компонента (В) в сторону которого обращена вершина звезды. Кристаллизация на поверхностях двунасыщения и линиях тройных эвтектик при подъеме фигуративной точки жидкой фазы к вершине звезды протекает по перетектиче-ским схемам. Например, путь кристаллизации сплава М на диаграмме плавкости со звездой четверного подъема (рис. 231) пролегает по кривой Мшт Е. На участке Мт при охлаждении сплава происходит выделение кристаллов компонента В. На участке тт протекает перитектическая реакция [c.414] Трехфазные трансформаторы (стр. 879) в виду толчкообразно чередующейся нагрузки отдельных фаз включается по схеме треугольник-звезаа, звезда-зигзаг. При больших мощностях тре-угольник-шестифазная звезда, звезда-шестифазный зигзаг, звезда-двойная, звезда с разделяющей ток дроссельной катушкой (отсасывающая катушка — ВВС) или двемадцатифазная звезда (АЕО) 1). [c.894] Наиболее рациональными схемами для выпрямления трехфазного тока является схема звезда — зигзаг, а для шестифазного — треугольник — дйойная звезда и звезда — двойной зигзаг. Использование трехфазной мостовой схемы Для питания в.акуумных дуговых печей нецелесообразно, так как при этом требуется удвоение числа вентилей. [c.72] Есть еще один фактор, который мы должны рассмотреть относительно возможных планетарных систем Поскольку на основании подробного исследования света, который звезда нам посылает, довольно легко обнаружить ее вращение, то точно так же мы можем обнаружить двойные звезды, то есть, две звезды, находящиеся довольно близко к друг другу, которые вращаются друг вокруг друга и удерживаются на своих орбитах взаимным гравитационным притяжением Обе звезды не обязательно должны быть одинакового размера или типа, и на поверку они часто несколько отличаются друг от друга Оказывается, что такие сложные системы довольно распространены, являясь скорее почти правилом, чем исключением. Итак, планетарная система, вращающаяся вокруг пары звезд, которые вращаются друг вокруг друга, вероятно, окажется несколько менее устоичивои по сравнению с такой как наша, которая имеет в своем центре только одиночную звезду Двойные звезды, если они не находятся очень близко к друг другу (в этом случае их гравитационное воздействие на планеты приближается к действию одиночной звезды), могут возмущать орбиты планет, поскольку иногда планета будет находиться ближе к одной звезде, а затем, немного поз же, к другой. Это не только приведет к тому, что энергия, падающая на определенную планету, может периодически изменяться, но, что еще важнее, возрастет опасность столкновения планет друг с другом. Постоянные условия в течение длительных периодов времени, которые, как мы полагаем, необходимы для развития высших форм жизни, не могут с легкостью возникнуть в таких планетарных системах. Таким образом, несмотря на то, что многие двойные звезды могут иметь планеты, они могут оказаться не идеальными для развития жизни. Конечно, некоторые колебания, как мы знаем, могут оказаться полезной вещью, и время от времени могут резко двигать эволюцию вперед, но трудно поверить, что какая-либо форма жизни переживет реальное столкновение двух планет. [c.83] R — расстояние от центра инерции двойной звезды - постоян- [c.60] Интересно обсудить, как скоро этот подход может быть реализован. Новые продукты, полученные в результате клиппинг -реакции из колец с более чем тремя полуоборотами, обсуждены в работах [2, 11]. Среди них катенаны с двойными и тройными петлями и цикл в виде пя-1 иконечной звезды, как показано на схеме 14. Несомненно, разделить скрученные цилиндры и мёбиусовы ленты будет намного труднее, поскольку образуется больше изомеров. Кроме того, станет проблематичным доказательство структуры. Например, как отличить один от другого трилистный узел и изо- [c.44] Джерасси и сотр. [2] использовали этот метод введения д9(1 )-двойной связи в синтезе днацетата (5) природного генина морской звезды — A ( ) Пpeгнeн-5a-диoл-3(3,6a-oнa-20 [3] из соединения (4). [c.239] Сульфат галлия кристаллизуется из растворов в виде 0а2(304)з-пН20, образуя мягкие белые пластинки или звезды. Количество молекул воды в этом соединении зависит от температуры кристаллизации. При комнатной температуре из растворов осаждается сульфат состава Оа2(804)з-20Н20. При нагре вании почти вся вода удаляется безводная соль выше 520° С разлагается с отщеплением ЗОз. При высокой температуре сульфат в значительной степени летуч [423, 1254]. С сульфатами одновалентных металлов и аммония сульфат галлия легко образует двойные соли типа квасцов МОа (504)2 12Н2О [74]. Квасцы галлия в разбавленных растворах практически полностью диссоциируют на ионы. [c.18] Электрическая схема выпрямителя типа ВАКГ приведена на рис. 5.3. Вторичные обмотки силового понижающего трансформатора Т4 вместе с кремниевыми диодами VI—У6 образуют выпрямитель по схеме двойная звезда с уравнительным реактором Ь. Для плавного изменения выпрямленного напряжения в каждую фазу включены рабочие обмотки — S7p6 дросселей насыщения. Управление осуществляется посредством обмоток смещения 1 ус и обмотки управления Wy. Последние являются нагрузкой промежуточного магнитного усилителя МУ, собранного по схеме самонасыщения. Для поддержания жесткости вольт-ампер-ных характеристик схема выполнена в виде замкнутой системы автоматического регулирования с обратными связями по току и напряжению. Цепь обратной связи по току состоит из трех трансформаторов тока Т1—ТЗ, трех диодов и потенциометра Н1. С этого потенциометра снимается напряжение, пропорциональное току нагрузки, и подается на обмотку управления Фз магнитного усилителя МУ. На обмотку 7 подается сигнал, пропорциональный напряжению на шинах выпрямителя. Обмотки 4, являются задающими, напряжение на них регулируется резистором Н2. Все обмотки магнитного усилителя подключены таким образом, что при росте нагрузки автоматически увеличивается сила тока управления в обмотке управления силового магнитного усилителя, что приводит к компенсации падения выпрямленного напряжения. Реле К2 отключает выпрямитель от сети при токовой перегрузке. Струйное реле КС дает разрешение на включение выпрямителя только при работе вентилятора или подаче воды. [c.181] На рис. XXIX.14, а изображена диаграмма плавкости двойной системы с образованием недиссоциированного соединения АВ, которому отвечает сингулярная точка т. При сложении вторичных диаграмм, на которые можно разложить первичную (см. гл. VIII), координатные симплексы вторичных систем АМ и МБ складываются в линейное древо АМВ, которое в данном случае представляет отрезок прямой, так как угол между АМ и МБ равен нулю, а с точки зрения топологии величина угла между складываемыми отрезками несущественна. Двухлучевые фазовые звезды с вершинами Е- и Ео, складываясь, дают незамкнутое линейное древо А — Ej — — В. [c.462] В случае кратных звезд данные относятся ко вс й системе в,,целом. Обозначения следующие Виз. дв. — визуально-двойная Сп. дв. — спектрально-двойная Чет. — четырехкомпонентная система Перем. — пере- менная Виз. тр. — визуадьно-тройная. [c.981] Из сказанного ясно, что гелий Не , медленно образующийся на Солнце из водорода, будет постепенно накапливаться, так как ядра Не не вступают во взаимодействие с ядрами Н . Даже при достаточной концентрации ядер He когда сделаются вероятными их взаимные двойные соударения, Ве образовываться не будет. Эволюция элементов в направлении дальнейшего их усложнения за пределы четырехнуклонных ядер Не как полагают, уже не характерна для Солнца и происходит лишь на более массивных, чем Солнце, и более горячих звездах, на которых температура достигает 10 градусов (на Солнце она даже во внутренних его частях, видимо, не выше, чем З-Ю градусов). Более высокая температура позволяет преодолеть взаимное электростатическое отталкивание трех а.2+-частиц при их одновременном соударении, которое хотя и будет менее вероятно, чем бинуклидные столкновения, но все же [c.207] Долгое время думал над этой загадкой и Браунер в ходе своих длительных и многочисленных исследований редкоземельных металлов и их соединений. В итоге всех своих исследований Браунер пришел к мысли выделить все эти элементы в совершенно особую, замкнутую-группу и поместить ее в одной большой клетке, расположенной в середине периодической системы в виде особой интер-периодической группы. Это — будущая укороченная таблица элементов. Верный взглядам Менделеева, Браунер привлек в качестве подтверждения правомерности своей идеи аналогию с миром небесных тел, как это делал Менделеев, когда он сравнивал невидимый мир атомов с видимым миром небесных тел — звезд, планет, спутников,, звездных туманностей, солнечных систем и систем двойных звезд. Подобно тому,— говорил Браунер в декабре 1901 г.,— как в солнечной системе целая группа астероидов занимает полосу на месте пути, по которому по ана-.тогии должна была бы двигаться одна планета, так [c.99] В обеих структурах такие звезды объединяются попарно, но различным способом в М017О47 сопряжением по общему ребру двух октаэдров, в Nbl6Wl8094 — сопряжением по двум вершинам соседних октаэдров. Способ взаимного расположения двойных звезд в этих структурах почти одинаков. [c.16] chem21.info Звезды альфа Центавра (слева) и Хадар (справа) на фоне Млечного Пути Двойные звезды – достаточно распространенные объекты в наблюдаемой Вселенной. Но, невзирая на это, они вызывают неподдельный интерес у астрономов всего мира. Двойная система из О-звёзд в представлении художника Ученые утверждают, что двойные звезды составляют примерно половину всех звезд нашей галактики. Двойная звезда представляет собой систему, состоящую из двух объектов (звезд), связанных между собой гравитационными силами. Обе звезды, входящие в систему, вращаются вокруг общего центра их масс. Расстояния между звездами могу отличаться, равно как и масса этих звезд, а также их размеры. Обе звезды, входящие в гравитационную систему, могут иметь, как схожие, так и отличительные характеристики. Например, звезда А может иметь большую массу или размер, чем звезда В. Двойные звезды помечают латинскими буквами традиционно. Обычно буквой «А» помечают более яркого и массивного компаньона. Буквой «В» — менее яркую и массивную звезду. Сириус А и В Ярким примером системы двойной звезды выступает ближайшая к нам звездная система – Альфа Центавра А и В. Она представляет собой целостную систему из двух звезд. Сама же Альфа Центавра состоит из трех компонентов. Если взглянуть на эту звезду, не прибегая к помощи различных оптических приборов, невооруженным глазом она будет визуально восприниматься, как одна звезда. Если посмотреть на нее через телескоп, то мы отчетливо увидим два, а то и три компонента этой системы. В качестве других примеров двойных звезд можно привести систему Бета Лиры, систему Бета Персея (Алголь), Сириус и другие звезды. Астрономами было уже давно обнаружено, что двойные звезды могут отличаться по типу своего происхождения, физическим параметрам и прочим характеристикам. По этой причине ученые предложили классифицировать эти объекты небесной сферы. Условно двойные звезды разделяют на два типа: звезды, между которыми не происходит обмена масс, и звезды, между которыми он происходит, происходил или будет происходить в будущем. Последние, в свою очередь, подразделяются на контактные и полуразделенные. В контактных системах обе звезды заполняют свои полости Роша. В полуразделенных – только одна звезда. Помимо представленной выше классификации, двойные звезды можно разделить по способу их наблюдения. Так, существуют астрометрические, затемненные, спектральные и визуальные двойные звезды. Астрометрические двойные звезды обнаруживаются на небе путем наблюдения изменений и нелинейности движения видимого объекта системы. Таким способом часто астрономы обнаруживают коричневые карлики, которые иными путями зафиксировать не удается. Затемненные двойные звезды можно обнаружить путем фиксации изменения блеска в паре звезд. Во время вращения звезды-компаньоны как бы затмевают друг друга, и за счет этого выдают себя, как двойная звезда. Метод спектрального обнаружения двойной звезды заключается в измерении на протяжении нескольких ночей. Смещение линий спектра звезды на протяжении некоторого времени, большая разница между минимальной и максимальной скоростью звезды, изменение лучевых скоростей – все это может указать на то, что наблюдаемое нами небесное тело – двойная звезда. Визуальный метод обнаружения двойных звезд самый простой. При помощи мощного телескопа мы можем обнаружить двойные звезды, которые удобны для визуального наблюдения и находятся на сравнительно недалеком от нас расстоянии. Интересным феноменом, который тесно связан с двойными звездами, является парадокс Алголя. Алголь – это двойная звезда, которая находится в созвездии Персея. Согласно общей теории эволюции небесных светил, чем больше масса звезды, тем быстрее она проходит все стадии эволюции. Но Парадокс Алголя заключается в том, что Алголь В – компонент двойной звезды, который обладает меньшей массой, эволюционно старше более массивного компонента этой системы – Алголь А. Ученые считают, что данный парадокс напрямую связан с эффектом перетекания масс в тесных двойных системах, за счет которого меньшая по размерам звезда могла эволюционировать быстрее более массивного компонента системы. Сечение поверхностей равного потенциала в модели Роша в орбитальной плоскости двойной системы С Парадоксом Алголя тесно связано еще одно интересное астрономическое явление, свойственное двойным звездам – это обмен массами между ними. Компоненты двойных звезд способны обмениваться своими массами и частицами друг с другом. У каждого из компонентов есть полость Роша – область, в которой гравитационные силы одного компаньона преобладают над гравитационными силами другого. Точка соприкосновения полостей Роша обеих звезд именуется точкой Лагранжа. Через эту точку возможно перетекание вещества одного компаньона к другому. Интересным явлением, связанным с двойными звездами, можно также считать симбиотические системы двойных звезд. Данные системы состоят, как правило, из красного гиганта и белого карлика, которые вращаются вокруг общего центра масс. Продолжительность жизни таких систем сравнительно невелика. Однако для них характерны новоподобные вспышки, которые способны увеличить яркость звезды в 2-3 раза. Кроме того, симбиотическим двойным звездам свойственны и другие интересные астрофизические характеристики, которые привлекают умы астрономов всего земного шара. Происхождение и эволюция двойных звезд происходит, в принципе, по тому же сценарию, что и у обычных звезд. Однако есть некоторые нюансы, которые отличают происхождение и эволюцию двойных систем от происхождения и эволюции одиночных светил. Эволюция тесной двойной системы в представлении художника Как и одинарные звезды, двойные системы образуются под влиянием гравитационных сил из газопылевого облака. В современной астрономии существует три наиболее популярных теории образования двойных звезд. Первая из них связывает образование двойных систем с разделением на раннем этапе общего ядра протооблака, которое послужило материалом для возникновения двойной системы. Вторая теория связана с фрагментацией протозвездного диска, в результате чего могут появиться не только двойные, но и многократные системы звезд. Происходит фрагментация протозвездного диска на более позднем этапе, чем фрагментация ядра. Последняя теория гласит, что образование двойных звезд возможно путем динамических физико-химических процессов внутри протооблака, которое служит материалом для образования звезд. Вид с экзопланеты Kepler 47c на двойную звезду Экзопланеты – это планеты, которые находятся вне пределов Солнечной системы. На сегодняшний день известно свыше 800 таких планет. Считается, что 64 из них вращаются вокруг систем двойных звезд. Среди этих планет существуют объекты, которые вращаются вокруг только одного компаньона двойной звездной системы, а также объекты, орбита которых огибает сразу два компонента звездной системы. Считается, что экзопланеты вокруг двойных звезд образуются путем разделения протопланетного диска. Большая часть экзопланет в двойных системах, где расстояние между звездами-компаньонами достигает 35-100 астрономических единиц, находятся на расстоянии около 20 астрономических единиц от одной или обоих звезд-компаньонов. В широких двойных звездных системах экзопланеты всегда одиночные. Мицар и Алькор — одни из самых знаменитых двойных звезд Впервые выдвинул гипотезу о существовании систем двойных звезд английский астроном Джон Митчелл еще в 1767 году. Доказательством этой гипотезы послужили наблюдения, произведенные в 1802 году другим британским физиком Уильямом Гершелем. В период с XIX по XX век ученые активно изучали двойные звезды. Успешности проведения их исследований способствовали новые мощные оптические приборы. Современный анализ и исследование двойных звезд осуществляется астрономами не только путем визуального их наблюдения, но и также путем астрометрического и спектрального анализа данных систем. Если первый способ эффективен для обнаружения и исследования ближайших к Земле систем двойных звезд, то вторые два незаменимы при анализе и исследовании отдаленных и трудно наблюдаемых систем двойных звезд. comments powered by HyperComments Понравилась запись? Расскажи о ней друзьям! Просмотров записи: 5061 spacegid.com Двойная звезда, или двойная система, — система из двух гравитационно связанных звёзд, обращающихся по замкнутым орбитам вокруг общего центра масс. Двойные звёзды — весьма распространённые объекты. Примерно половина всех звёзд нашей Галактики принадлежит к двойным системам[1]. Измерив период обращения и расстояние между звёздами, иногда можно определить массы компонентов системы. Этот метод практически не требует дополнительных модельных предположений, и поэтому является одним из главных методов определения масс в астрофизике. По этой причине двойные системы, компонентами которых являются чёрные дыры или нейтронные звёзды, представляют большой интерес для астрофизики. Физически двойные звезды можно разделить на два класса[2]: Двойные системы также классифицируются по способу наблюдения, можно выделить визуальные, спектральные, затменные, астрометрические двойные системы. Двойные звезды, которые возможно увидеть раздельно (или, как говорят, которые могут быть разрешены), называются видимыми двойными, или визуально-двойными. Возможность наблюдать звезду как визуально-двойную определяется разрешающей способностью телескопа, расстоянием до звёзд и расстоянием между ними. Таким образом, визуально-двойные звезды — это в основном звезды окрестностей Солнца с очень большим периодом обращения (следствие большого расстояния между компонентами). Из-за большого периода проследить орбиту двойной можно только по многочисленным наблюдениям на протяжении десятков лет. На сегодняшний день в каталогах WDS и CCDM свыше 78 000 и 110 000 объектов соответственно, и только у нескольких сотен из них можно вычислить орбиту. У менее чем сотни объектов орбита известна с достаточной точностью, чтобы получить массу компонентов. При наблюдениях визуально-двойной звезды измеряют расстояние между компонентами и позиционный угол линии центров, иначе говоря, угол между направлением на северный полюс мира и направлением линии, соединяющей главную звезду с её спутником. Спекл-интерферометрия наряду с адаптивной оптикой позволяет достичь дифракционного предела разрешения звёзд, что в свою очередь позволяет обнаруживать двойные звезды. Таким образом, спекл-интерферометрические двойные — это тоже визуально-двойные. Но если в классическом визуально-двойном методе необходимо получить два отдельных изображения, то в данном случае приходится анализировать спекл-интерферограммы[1]. Спекл-интерферометрия эффективна для двойных с периодом в несколько десятков лет.[3] В случае визуально-двойных звёзд мы видим перемещение по небу сразу двух объектов. Однако, если представить себе, что один из двух компонентов нам не виден по тем или иным причинам, то двойственность все равно можно обнаружить по изменению положения на небе второго. В таком случае говорят об астрометрически-двойных звёздах. Если наличествуют высокоточные астрометрические наблюдения, то двойственность можно предположить, зафиксировав нелийность движения: первую производную собственного движения и вторую[прояснить][4]. Астрометрические двойные звезды используются для измерения массы коричневых карликов разных спектральных классов[5]. Спектрально-двойной называют звезду, двойственность которой обнаруживается при помощи спектральных наблюдений. Для этого её наблюдают в течение нескольких ночей. Если оказывается, что линии её спектра периодически смещаются со временем, то это означает, что скорость источника меняется. Этому может быть множество причин: переменность самой звезды, наличие у неё плотной расширяющейся оболочки, образовавшейся после вспышки сверхновой, и т. п. Если получен спектр второй компоненты, который показывает аналогичные смещения, но в противофазе, то можно с уверенностью говорить, что перед нами двойная система. Если первая звезда к нам приближается и её линии сдвинуты в фиолетовую сторону спектра, то вторая — удаляется, и её линии сдвинуты в красную сторону, и наоборот. Но если вторая звезда сильно уступает по яркости первой, то мы имеем шанс её не увидеть, и тогда нужно рассмотреть другие возможные варианты. Главный признак двойной звезды — периодичность изменения лучевых скоростей и большая разница между максимальной и минимальной скоростью. Но, строго говоря, не исключено, что обнаружена экзопланета. Чтобы это выяснить, надо вычислить функцию масс, по которой можно судить о минимальной массе невидимого второго компонента и, соответственно, о том, чем он является — планетой, звездой или даже чёрной дырой. Также по спектроскопическим данным, помимо масс компонентов, можно вычислить расстояние между ними, период обращения и эксцентриситет орбиты. Угол наклона орбиты к лучу зрения выяснить по этим данным невозможно. Поэтому о массе и расстоянии между компонентами можно говорить только как о вычисленных с точностью до угла наклона. Как и для любого типа объектов, изучаемых астрономами, существуют каталоги спектрально-двойных звёзд. Самый известный и самый обширный из них — «SB9» (от англ. Spectral Binaries). По состоянию на 2013 год в нём 2839 объектов. Бывает, что орбитальная плоскость наклонена к лучу зрения под очень маленьким углом: орбиты звёзд такой системы расположены как бы ребром к нам. В такой системе звёзды будут периодически затмевать друг друга, то есть блеск пары будет меняться. Двойные звёзды, у которых наблюдаются такие затмения, называются затменно-двойными или затменно-переменными. Самой известной и первой открытой звездой такого типа является Алголь (Глаз Дьявола) в созвездии Персея. Если на луче зрения между звездой и наблюдателем находится тело с сильным гравитационным полем, то объект будет линзирован. Если бы поле было сильным, то наблюдались бы несколько изображений звезды, но в случае галактических объектов их поле не настолько сильное, чтобы наблюдатель смог различить несколько изображений, и в таком случае говорят о микролинзировании. В случае, если гравирующее тело — двойная звезда, кривая блеска, получаемая при прохождении её вдоль луча зрения, сильно отличается от случая одиночной звезды[6]. С помощью микролинзирования ищутся двойные звезды, где оба компонента — маломассивные коричневые карлики[7]. Этот парадокс сформулирован в середине 20 века советскими астрономами А. Г. Масевич и П. П. Паренаго, обратившими внимание на несоответствие масс компонентов Алголя и их эволюционной стадии. Согласно теории эволюции звёзд, скорость эволюции массивной звезды гораздо больше, чем у звезды с массой, сравнимой с солнечной, или немногим более. Очевидно, что компоненты двойной звезды образовались в одно и то же время, следовательно, массивный компонент должен проэволюционировать раньше, чем маломассивный. Однако в системе Алголя более массивный компонент был моложе. Объяснение этого парадокса связано с феноменом перетекания масс в тесных двойных системах и впервые предложено американским астрофизиком Д. Кроуфордом. Если предположить, что в ходе эволюции у одного из компонентов появляется возможность переброса массы на соседа, то парадокс снимается[8]. Рассмотрим приближение тесной двойной системы (носящие имя приближения Роша): Тогда для компонентов M1 и M2 с суммой больших полуосей a=a1+a2 введем систему координат, синхронную с орбитальным вращением ТДС. Центр отсчета находится в центре звезды M1, ось X направлена от M1 к M2, а ось Z — вдоль вектора вращения. Тогда запишем потенциал, связанный с гравитационными полями компонентов и центробежной силой[2]: Φ=−GM1r1−GM2r2−12ω2[(x−μa)2+y2]{\displaystyle \Phi =-{\frac {GM_{1}}{r_{1}}}-{\frac {GM_{2}}{r_{2}}}-{\frac {1}{2}}\omega ^{2}\left[(x-\mu a)^{2}+y^{2}\right]} , где r1= √x2+y2+z2 , r2= √(x-a)2+y2+z2 , μ= M2/(M1+M2), а ω — частота вращения по орбите компонентов. Используя третий закон Кеплера, потенциал Роша можно переписать следующим образом: Φ=−12ω2a2ΩR{\displaystyle \Phi =-{\frac {1}{2}}\omega ^{2}a^{2}\Omega _{R}} , где безразмерный потенциал: ΩR=2(1+q)(r1/a)+2(1+q)(r2/a)+(x−μa)2+y2a2{\displaystyle \Omega _{R}={\frac {2}{(1+q)(r_{1}/a)}}+{\frac {2}{(1+q)(r_{2}/a)}}+{\frac {(x-\mu a)^{2}+y^{2}}{a^{2}}}} , где q = M2/M1 Эквипотенциали находятся из уравнения Φ(x,y,z)=const. Вблизи центров звёзд они мало отличаются от сферических, но по мере удаления отклонения от сферической симметрии становятся сильнее. В итоге обе поверхности смыкаются в точке Лагранжа L1. Это означает, что потенциальный барьер в этой точке равен 0, и частицы с поверхности звезды, находящие вблизи этой точки, способны перейти внутрь полости Роша соседней звезды, вследствие теплового хаотического движения[2]. Взаимодействующие двойные системы, состоящие из красного гиганта и белого карлика, окруженных общей туманностью. Для них характерны сложные спектры, где наряду с полосами поглощения (например, TiO) присутствуют эмиссионные линии, характерные для туманностей (ОIII, NeIII и т. п. Симбиотические звёзды являются переменными с периодами в несколько сотен дней, для них характерны новоподобные вспышки, во время которых их блеск увеличивается на две-три звёздных величины. Симбиотические звёзды представляют собой относительно кратковременный, но чрезвычайно важный и богатый своими астрофизическими проявлениями этап в эволюции двойных звёздных систем умеренных масс с начальными периодами обращения 1—100 лет. Механизм формирования одиночной звезды изучен довольно хорошо — это сжатие молекулярного облака из-за гравитационной неустойчивости. Также удалось установить функцию распределения начальных масс. Очевидно, что сценарий формирования двойной звезды должен быть таким же, но с дополнительными модификациями. Также он должен объяснять следующие известные факты[9]: На данный момент нет окончательного понимания, какие именно надо вносить модификации, и какие факторы и механизмы играют здесь решающую роль. Все предложенные на данный момент теории можно поделить по тому, какой механизм формирования в них используется[10]: Самый многочисленный класс теорий. В них формирование идет за счёт быстрого или раннего разделение протооблака. Самая ранняя из них считает, что в ходе коллапсирования из-за различного рода нестабильностей облако распадается на локальные джинсовские массы, растущие до тех пор, пока наименьшая из них перестанет быть оптически прозрачной и более не может эффективно охлаждаться. Но при этом расчетная функция масс звёзд не совпадает с наблюдаемой. Ещё одна из ранних теорий предполагала размножение коллапсирующих ядер, вследствие деформации в различные эллиптические фигуры. Современные же теории рассматриваемого типа считают, что основная причина фрагментации — рост внутренней энергии и энергии вращения по мере сжатия облака[10]. В теориях с динамическим диском образование происходит в ходе фрагментации протозвёздного диска, то есть гораздо позднее, чем в теориях с промежуточным ядром. Для этого необходим довольно массивный диск, восприимчивый к гравитационным нестабильностям, и газ которого эффективно охлаждается. Тогда могут возникнуть несколько компаньонов, лежащих в одной плоскости, которые аккрецируют газ из родительского диска. В последнее время количество компьютерных расчетов подобных теорий сильно увеличилось. В рамках подобного подхода хорошо объясняется происхождение тесных двойных систем, а также иерархических систем различной кратности. Последний механизм предполагает, что двойные звезды образовались в ходе динамических процессов, спровоцированных соревновательной аккрецией. В данном сценарии предполагается, что молекулярное облако из-за различного рода турбуленций внутри него формирует сгустки приблизительно джинсовской массы. Эти сгустки, взаимодействуя между собой, соревнуются за вещество исходного облака. В таких условиях хорошо работает как уже упомянутая модель с промежуточным диском, так и иные механизмы, речь о которых пойдет ниже. Вдобавок динамическое трение протозвёзд с окружающим газом сближает компоненты. В качестве одного из механизмов, работающего в данных условиях, предлагается комбинация фрагментации с промежуточным ядром и динамической гипотезы. Это позволяет воспроизвести частоту кратных звёзд в звёздных скоплениях. Однако на данный момент механизм фрагментации точно не описан. Другой механизм предполагает рост сечения гравитационного взаимодействия у диска до тех пор, пока не будет захвачена близлежащая звезда. Хотя такой механизм вполне подходит для массивных звёзд, но совершенно не годится для маломассивных и вряд ли является доминирующим при образовании двойных звёзд[10]. Из более чем 800 ныне известных экзопланет число обращающихся вокруг одиночных звёзд значительно превышает число планет, найденных в звёздных системах разной кратности. По последним данным последних насчитывается 64[11]. Экзопланеты в двойных системах принято разделять по конфигурациям их орбит[11]: Если попытаться провести статистику, то выяснится[11]: Обрезание протопланетного диска. В то время как у одиночных звёзд протопланетный диск может тянуться вплоть до пояса Койпера (30-50 а. е.), то в двойных звёзд его размер обрезается воздействием второго компонента. Таким образом протяжённость протопланетного диска в 2-5 раз меньше расстояния между компонентами. Искривление протопланетного диска. Оставшийся после обрезания диск продолжает испытывать влияние второго компонента и начинает вытягиваться, деформироваться, сплетаться и даже разрываться. Также такой диск начинает прецессировать. Сокращения время жизни протопланетного диска. Для широких двойных, как и для одиночных время жизни протопланетного диска составляет 1-10 млн лет. Одна для систем с разделением < 40 а. е. Время жизни диска должно составлять в пределах 0,1-1 млн лет. Существуют сценарии, в которых изначальная, сразу после формирования, конфигурация планетной системы отличается от текущей и была достигнута в ходе дальнейшей эволюции. В случае, когда двойная звезда является затменной, то становится возможным построить зависимость интегрального блеска от времени. Переменность блеска на этой кривой будет зависеть от [12]: Однако анализ только самих затмений, когда компоненты сферически симметричны и отсутствуют эффекты отражения, сводится к решению следующей системы уравнений[12]: 1−l1(Δ)=∬S(Δ)Ia(ξ)Ic(ρ)dσ{\displaystyle 1-l_{1}(\Delta )=\iint \limits _{S(\Delta )}I_{a}(\xi )I_{c}(\rho )d\sigma } 1−l2(Δ)=∬S(Δ)Ic(ξ)Ia(ρ)dσ{\displaystyle 1-l_{2}(\Delta )=\iint \limits _{S(\Delta )}I_{c}(\xi )I_{a}(\rho )d\sigma } ∫0rξcIc(ξ)2πξdξ+∫0rρcIc(ρ)2πρdρ=1{\displaystyle \int \limits _{0}^{r_{\xi c}}I_{c}(\xi )2\pi \xi d\xi +\int \limits _{0}^{r_{\rho c}}I_{c}(\rho )2\pi \rho d\rho =1} где ξ, ρ — полярные расстояния на диске первой и второй звезды, Ia — функция поглощения излучения одной звезды атмосферой другой, Ic — функция яркости площадок dσ у различных компонентов, Δ — область перекрытия, rξc,rρc — полные радиусы первой и второй звезды. Решение этой системы без априорных предположений невозможно. Ровно как и анализ более сложных случаев с элипсоидальной формой компонентов и эффектами отражения, существенных в различных вариантах тесных двойных систем. Поэтому все современные способы анализа кривых блеска тем или иным образом вводят модельные предположения, параметры которых находят путём другого рода наблюдений[12]. Если двойная звезда наблюдается спектроскопически, то есть является спектроскопической двойной звездой, то можно построить зависимость изменения лучевых скоростей компонентов от времени. Если предположить, что орбита круговая, то можно записать следующее[2]: Vs=V0sin(i)=2πPasin(i){\displaystyle V_{s}=V_{0}sin(i)={\frac {2\pi }{P}}asin(i)} , где Vs — лучевая скорость компонента, i — наклонение орбиты к лучу зрения, P — период, a — радиус орбиты компонента. Теперь, если в эту формулу подставить третий закон Кеплера, имеем: Vs=2πPMsMs+M2sin(i){\displaystyle V_{s}={\frac {2\pi }{P}}{\frac {M_{s}}{M_{s}+M_{2}}}sin(i)} , где Ms — масса исследуемого компонента, M2 — масса второго компонента. Таким образом, наблюдая оба компонента можно определить соотношение масс звёзд, составляющих двойную. Если повторно использовать третий закон Кеплера, то последние приводится к следующему: f(M2)=PVs12πG{\displaystyle f(M_{2})={\frac {PV_{s1}}{2\pi G}}} , где G -гравитационная постоянна, а f(M2) — функция масс звезды и по определению равна: f(M2)≡(M2sin(i))3(M1+M2)2{\displaystyle f(M_{2})\equiv {\frac {(M_{2}sin(i))^{3}}{(M_{1}+M_{2})^{2}}}} . В случае, если орбита не круговая, а имеет эксцентриситет, то можно показать, что для функции масса орбитальный период P должен быть домножен на фактор (1−e2)3/2{\displaystyle (1-e^{2})^{3/2}} . Если второй компонент не наблюдается, то функция f(M2) служит нижним пределом его массы. Стоит отметить, что изучая только кривые лучевых скоростей невозможно определить все параметры двойной системы, всегда будет присутствовать неопределённость в виде неизвестного угла наклонения орбиты[2]. Практически всегда гравитационное взаимодействие между двумя звёздами описывается с достаточной точностью законами Ньютона и законами Кеплера, являющимися следствием законов Ньютона. Но для описания двойных пульсаров (см. пульсар Тейлора-Халса) приходится привлекать ОТО. Изучая наблюдательные проявления релятивистских эффектов, можно ещё раз проверить точность теории относительности. Третий закон Кеплера связывает период обращения с расстоянием между компонентами и массой системы: где P{\displaystyle P} — период обращения, a{\displaystyle a} — большая полуось системы, M1{\displaystyle M_{1}} и M2{\displaystyle M_{2}} — массы компонентов, G{\displaystyle G} — гравитационная постоянная. Для визуально-двойной системы есть возможность определить орбиты обоих компонентов, рассчитать период и полуось, а также отношение масс. Но часто о двойственности системы можно судить только по спектральным данным (спектрально-двойные). По движению спектральных линий можно определить лучевые скорости одного компонента, а в редких случаях и сразу двух компонентов. Если известна лучевая скорость только одного компонента, то полную информацию о массах получить нельзя, но можно построить функцию масс и определить верхнюю границу массы второго компонента, а значит сказать, может ли он являться чёрной дырой или нейтронной звездой. Первым выдвинул идею о существовании двойных звёзд Джон Мичелл (Reverend John Michell). На выступлении в Королевском обществе в 1767 году он предположил, что многие звезды, видимые как двойные, действительно могут быть физически связаны. Наблюдательные подтверждения этой гипотезы были опубликованы сэром Уильямом Гершелем в 1802[13]. ru-wiki.org Фото by Sylenomelori На нашем сайте мы уже не раз знакомили читателей с подвижными поделками в стиле флексагонов, которые, словно калейдоскоп, могут бесконечно много раз переворачиваться, создавая все новые творения. Хотим показать вам еще одну интересную модель, которую изобрел Девид Бриль (David Brill), под названием Double Star Flexicube или Двойная Звезда Флексикуб. Эта невероятная поделка путем простых движений руками может превращаться в несколько кубиков, соединенных между собой, две соединенные звезды или даже кусудаму с шипами. О том, как именно складывается такая модель, мы расскажем в этом посте. Для сборки такого флексикуба вам понадобится: Девид Бриль создал эту движущуюся модель по аналогии с известными кубиками Naoki Yoshimoto, которые были изобретены в 1971 году. То, что мы собираемся с вами сложить, является своего рода оригами-интерпретацией Девида поделки Yoshimoto. Фото by ale_beber_origami Как видите, эта модель складывается не из традиционного для оригами квадрата. О том, как быстро и без проблем получить из любого А-формата меньший его аналог, можете узнать здесь, а здесь подробно показано, как получить А-формат из квадрата. Полюбившаяся многим, талантливая оригамистка Сара Адамс смонтировала подробный видео-урок по сборке такого флексикуба. Надеемся, после просмотра видео у вас не возникнет сложностей со сборкой такой модели. Кроме того, на сайте Девида Бриля есть подробные диаграммы сборки Двойной звезды флексикуба. Желаем удачи! Видео по сборке флексикуба: часть 1 Часть 2 Часть 3 planetaorigami.ru Двойная звезда, или двойная система, — система из двух гравитационно связанных звёзд, обращающихся по замкнутым орбитам вокруг общего центра масс. Двойные звёзды — весьма распространённые объекты. Примерно половина всех звёзд нашей Галактики принадлежит к двойным системам[1]. Измерив период обращения и расстояние между звёздами, иногда можно определить массы компонентов системы. Этот метод практически не требует дополнительных модельных предположений, и поэтому является одним из главных методов определения масс в астрофизике. По этой причине двойные системы, компонентами которых являются чёрные дыры или нейтронные звёзды, представляют большой интерес для астрофизики. Физически двойные звезды можно разделить на два класса[2]: Двойные системы также классифицируются по способу наблюдения, можно выделить визуальные, спектральные, затменные, астрометрические двойные системы. Двойные звезды, которые возможно увидеть раздельно (или, как говорят, которые могут быть разрешены), называются видимыми двойными, или визуально-двойными. Возможность наблюдать звезду как визуально-двойную определяется разрешающей способностью телескопа, расстоянием до звёзд и расстоянием между ними. Таким образом, визуально-двойные звезды — это в основном звезды окрестностей Солнца с очень большим периодом обращения (следствие большого расстояния между компонентами). Из-за большого периода проследить орбиту двойной можно только по многочисленным наблюдениям на протяжении десятков лет. На сегодняшний день в каталогах WDS и CCDM свыше 78 000 и 110 000 объектов соответственно, и только у нескольких сотен из них можно вычислить орбиту. У менее чем сотни объектов орбита известна с достаточной точностью, чтобы получить массу компонентов. При наблюдениях визуально-двойной звезды измеряют расстояние между компонентами и позиционный угол линии центров, иначе говоря, угол между направлением на северный полюс мира и направлением линии, соединяющей главную звезду с её спутником. Спекл-интерферометрия наряду с адаптивной оптикой позволяет достичь дифракционного предела разрешения звёзд, что в свою очередь позволяет обнаруживать двойные звезды. Таким образом, спекл-интерферометрические двойные — это тоже визуально-двойные. Но если в классическом визуально-двойном методе необходимо получить два отдельных изображения, то в данном случае приходится анализировать спекл-интерферограммы[1]. Спекл-интерферометрия эффективна для двойных с периодом в несколько десятков лет.[3] В случае визуально-двойных звёзд мы видим перемещение по небу сразу двух объектов. Однако, если представить себе, что один из двух компонентов нам не виден по тем или иным причинам, то двойственность все равно можно обнаружить по изменению положения на небе второго. В таком случае говорят об астрометрически-двойных звёздах. Если наличествуют высокоточные астрометрические наблюдения, то двойственность можно предположить, зафиксировав нелийность движения: первую производную собственного движения и вторую[прояснить][4]. Астрометрические двойные звезды используются для измерения массы коричневых карликов разных спектральных классов[5]. Спектрально-двойной называют звезду, двойственность которой обнаруживается при помощи спектральных наблюдений. Для этого её наблюдают в течение нескольких ночей. Если оказывается, что линии её спектра периодически смещаются со временем, то это означает, что скорость источника меняется. Этому может быть множество причин: переменность самой звезды, наличие у неё плотной расширяющейся оболочки, образовавшейся после вспышки сверхновой, и т. п. Если получен спектр второй компоненты, который показывает аналогичные смещения, но в противофазе, то можно с уверенностью говорить, что перед нами двойная система. Если первая звезда к нам приближается и её линии сдвинуты в фиолетовую сторону спектра, то вторая — удаляется, и её линии сдвинуты в красную сторону, и наоборот. Но если вторая звезда сильно уступает по яркости первой, то мы имеем шанс её не увидеть, и тогда нужно рассмотреть другие возможные варианты. Главный признак двойной звезды — периодичность изменения лучевых скоростей и большая разница между максимальной и минимальной скоростью. Но, строго говоря, не исключено, что обнаружена экзопланета. Чтобы это выяснить, надо вычислить функцию масс, по которой можно судить о минимальной массе невидимого второго компонента и, соответственно, о том, чем он является — планетой, звездой или даже чёрной дырой. Также по спектроскопическим данным, помимо масс компонентов, можно вычислить расстояние между ними, период обращения и эксцентриситет орбиты. Угол наклона орбиты к лучу зрения выяснить по этим данным невозможно. Поэтому о массе и расстоянии между компонентами можно говорить только как о вычисленных с точностью до угла наклона. Как и для любого типа объектов, изучаемых астрономами, существуют каталоги спектрально-двойных звёзд. Самый известный и самый обширный из них — «SB9» (от англ. Spectral Binaries). По состоянию на 2013 год в нём 2839 объектов. Бывает, что орбитальная плоскость наклонена к лучу зрения под очень маленьким углом: орбиты звёзд такой системы расположены как бы ребром к нам. В такой системе звёзды будут периодически затмевать друг друга, то есть блеск пары будет меняться. Двойные звёзды, у которых наблюдаются такие затмения, называются затменно-двойными или затменно-переменными. Самой известной и первой открытой звездой такого типа является Алголь (Глаз Дьявола) в созвездии Персея. Если на луче зрения между звездой и наблюдателем находится тело с сильным гравитационным полем, то объект будет линзирован. Если бы поле было сильным, то наблюдались бы несколько изображений звезды, но в случае галактических объектов их поле не настолько сильное, чтобы наблюдатель смог различить несколько изображений, и в таком случае говорят о микролинзировании. В случае, если гравирующее тело — двойная звезда, кривая блеска, получаемая при прохождении её вдоль луча зрения, сильно отличается от случая одиночной звезды[6]. С помощью микролинзирования ищутся двойные звезды, где оба компонента — маломассивные коричневые карлики[7]. Этот парадокс сформулирован в середине 20 века советскими астрономами А. Г. Масевич и П. П. Паренаго, обратившими внимание на несоответствие масс компонентов Алголя и их эволюционной стадии. Согласно теории эволюции звёзд, скорость эволюции массивной звезды гораздо больше, чем у звезды с массой, сравнимой с солнечной, или немногим более. Очевидно, что компоненты двойной звезды образовались в одно и то же время, следовательно, массивный компонент должен проэволюционировать раньше, чем маломассивный. Однако в системе Алголя более массивный компонент был моложе. Объяснение этого парадокса связано с феноменом перетекания масс в тесных двойных системах и впервые предложено американским астрофизиком Д. Кроуфордом. Если предположить, что в ходе эволюции у одного из компонентов появляется возможность переброса массы на соседа, то парадокс снимается[8]. Рассмотрим приближение тесной двойной системы (носящие имя приближения Роша): Тогда для компонентов M1 и M2 с суммой больших полуосей a=a1+a2 введем систему координат, синхронную с орбитальным вращением ТДС. Центр отсчета находится в центре звезды M1, ось X направлена от M1 к M2, а ось Z — вдоль вектора вращения. Тогда запишем потенциал, связанный с гравитационными полями компонентов и центробежной силой[2]: Φ=−GM1r1−GM2r2−12ω2[(x−μa)2+y2]{\displaystyle \Phi =-{\frac {GM_{1}}{r_{1}}}-{\frac {GM_{2}}{r_{2}}}-{\frac {1}{2}}\omega ^{2}\left[(x-\mu a)^{2}+y^{2}\right]}, где r1= √x2+y2+z2 , r2= √(x-a)2+y2+z2 , μ= M2/(M1+M2), а ω — частота вращения по орбите компонентов. Используя третий закон Кеплера, потенциал Роша можно переписать следующим образом: Φ=−12ω2a2ΩR{\displaystyle \Phi =-{\frac {1}{2}}\omega ^{2}a^{2}\Omega _{R}}, где безразмерный потенциал: ΩR=2(1+q)(r1/a)+2(1+q)(r2/a)+(x−μa)2+y2a2{\displaystyle \Omega _{R}={\frac {2}{(1+q)(r_{1}/a)}}+{\frac {2}{(1+q)(r_{2}/a)}}+{\frac {(x-\mu a)^{2}+y^{2}}{a^{2}}}}, где q = M2/M1 Эквипотенциали находятся из уравнения Φ(x,y,z)=const. Вблизи центров звёзд они мало отличаются от сферических, но по мере удаления отклонения от сферической симметрии становятся сильнее. В итоге обе поверхности смыкаются в точке Лагранжа L1. Это означает, что потенциальный барьер в этой точке равен 0, и частицы с поверхности звезды, находящие вблизи этой точки, способны перейти внутрь полости Роша соседней звезды, вследствие теплового хаотического движения[2]. Взаимодействующие двойные системы, состоящие из красного гиганта и белого карлика, окруженных общей туманностью. Для них характерны сложные спектры, где наряду с полосами поглощения (например, TiO) присутствуют эмиссионные линии, характерные для туманностей (ОIII, NeIII и т. п. Симбиотические звёзды являются переменными с периодами в несколько сотен дней, для них характерны новоподобные вспышки, во время которых их блеск увеличивается на две-три звёздных величины. Симбиотические звёзды представляют собой относительно кратковременный, но чрезвычайно важный и богатый своими астрофизическими проявлениями этап в эволюции двойных звёздных систем умеренных масс с начальными периодами обращения 1—100 лет. Механизм формирования одиночной звезды изучен довольно хорошо — это сжатие молекулярного облака из-за гравитационной неустойчивости. Также удалось установить функцию распределения начальных масс. Очевидно, что сценарий формирования двойной звезды должен быть таким же, но с дополнительными модификациями. Также он должен объяснять следующие известные факты[9]: На данный момент нет окончательного понимания, какие именно надо вносить модификации, и какие факторы и механизмы играют здесь решающую роль. Все предложенные на данный момент теории можно поделить по тому, какой механизм формирования в них используется[10]: Самый многочисленный класс теорий. В них формирование идет за счёт быстрого или раннего разделение протооблака. Самая ранняя из них считает, что в ходе коллапсирования из-за различного рода нестабильностей облако распадается на локальные джинсовские массы, растущие до тех пор, пока наименьшая из них перестанет быть оптически прозрачной и более не может эффективно охлаждаться. Но при этом расчетная функция масс звёзд не совпадает с наблюдаемой. Ещё одна из ранних теорий предполагала размножение коллапсирующих ядер, вследствие деформации в различные эллиптические фигуры. Современные же теории рассматриваемого типа считают, что основная причина фрагментации — рост внутренней энергии и энергии вращения по мере сжатия облака[10]. В теориях с динамическим диском образование происходит в ходе фрагментации протозвёздного диска, то есть гораздо позднее, чем в теориях с промежуточным ядром. Для этого необходим довольно массивный диск, восприимчивый к гравитационным нестабильностям, и газ которого эффективно охлаждается. Тогда могут возникнуть несколько компаньонов, лежащих в одной плоскости, которые аккрецируют газ из родительского диска. В последнее время количество компьютерных расчетов подобных теорий сильно увеличилось. В рамках подобного подхода хорошо объясняется происхождение тесных двойных систем, а также иерархических систем различной кратности. Последний механизм предполагает, что двойные звезды образовались в ходе динамических процессов, спровоцированных соревновательной аккрецией. В данном сценарии предполагается, что молекулярное облако из-за различного рода турбуленций внутри него формирует сгустки приблизительно джинсовской массы. Эти сгустки, взаимодействуя между собой, соревнуются за вещество исходного облака. В таких условиях хорошо работает как уже упомянутая модель с промежуточным диском, так и иные механизмы, речь о которых пойдет ниже. Вдобавок динамическое трение протозвёзд с окружающим газом сближает компоненты. В качестве одного из механизмов, работающего в данных условиях, предлагается комбинация фрагментации с промежуточным ядром и динамической гипотезы. Это позволяет воспроизвести частоту кратных звёзд в звёздных скоплениях. Однако на данный момент механизм фрагментации точно не описан. Другой механизм предполагает рост сечения гравитационного взаимодействия у диска до тех пор, пока не будет захвачена близлежащая звезда. Хотя такой механизм вполне подходит для массивных звёзд, но совершенно не годится для маломассивных и вряд ли является доминирующим при образовании двойных звёзд[10]. Из более чем 800 ныне известных экзопланет число обращающихся вокруг одиночных звёзд значительно превышает число планет, найденных в звёздных системах разной кратности. По последним данным последних насчитывается 64[11]. Экзопланеты в двойных системах принято разделять по конфигурациям их орбит[11]: Если попытаться провести статистику, то выяснится[11]: Обрезание протопланетного диска. В то время как у одиночных звёзд протопланетный диск может тянуться вплоть до пояса Койпера (30-50 а. е.), то в двойных звёзд его размер обрезается воздействием второго компонента. Таким образом протяжённость протопланетного диска в 2-5 раз меньше расстояния между компонентами. Искривление протопланетного диска. Оставшийся после обрезания диск продолжает испытывать влияние второго компонента и начинает вытягиваться, деформироваться, сплетаться и даже разрываться. Также такой диск начинает прецессировать. Сокращения время жизни протопланетного диска. Для широких двойных, как и для одиночных время жизни протопланетного диска составляет 1-10 млн лет. Одна для систем с разделением < 40 а. е. Время жизни диска должно составлять в пределах 0,1-1 млн лет. Существуют сценарии, в которых изначальная, сразу после формирования, конфигурация планетной системы отличается от текущей и была достигнута в ходе дальнейшей эволюции. В случае, когда двойная звезда является затменной, то становится возможным построить зависимость интегрального блеска от времени. Переменность блеска на этой кривой будет зависеть от [12]: Однако анализ только самих затмений, когда компоненты сферически симметричны и отсутствуют эффекты отражения, сводится к решению следующей системы уравнений[12]: 1−l1(Δ)=∬S(Δ)Ia(ξ)Ic(ρ)dσ{\displaystyle 1-l_{1}(\Delta )=\iint \limits _{S(\Delta )}I_{a}(\xi )I_{c}(\rho )d\sigma } 1−l2(Δ)=∬S(Δ)Ic(ξ)Ia(ρ)dσ{\displaystyle 1-l_{2}(\Delta )=\iint \limits _{S(\Delta )}I_{c}(\xi )I_{a}(\rho )d\sigma } ∫0rξcIc(ξ)2πξdξ+∫0rρcIc(ρ)2πρdρ=1{\displaystyle \int \limits _{0}^{r_{\xi c}}I_{c}(\xi )2\pi \xi d\xi +\int \limits _{0}^{r_{\rho c}}I_{c}(\rho )2\pi \rho d\rho =1} где ξ, ρ — полярные расстояния на диске первой и второй звезды, Ia — функция поглощения излучения одной звезды атмосферой другой, Ic — функция яркости площадок dσ у различных компонентов, Δ — область перекрытия, rξc,rρc — полные радиусы первой и второй звезды. Решение этой системы без априорных предположений невозможно. Ровно как и анализ более сложных случаев с элипсоидальной формой компонентов и эффектами отражения, существенных в различных вариантах тесных двойных систем. Поэтому все современные способы анализа кривых блеска тем или иным образом вводят модельные предположения, параметры которых находят путём другого рода наблюдений[12]. Если двойная звезда наблюдается спектроскопически, то есть является спектроскопической двойной звездой, то можно построить зависимость изменения лучевых скоростей компонентов от времени. Если предположить, что орбита круговая, то можно записать следующее[2]: Vs=V0sin(i)=2πPasin(i){\displaystyle V_{s}=V_{0}sin(i)={\frac {2\pi }{P}}asin(i)}, где Vs — лучевая скорость компонента, i — наклонение орбиты к лучу зрения, P — период, a — радиус орбиты компонента. Теперь, если в эту формулу подставить третий закон Кеплера, имеем: Vs=2πPMsMs+M2sin(i){\displaystyle V_{s}={\frac {2\pi }{P}}{\frac {M_{s}}{M_{s}+M_{2}}}sin(i)}, где Ms — масса исследуемого компонента, M2 — масса второго компонента. Таким образом, наблюдая оба компонента можно определить соотношение масс звёзд, составляющих двойную. Если повторно использовать третий закон Кеплера, то последние приводится к следующему: f(M2)=PVs12πG{\displaystyle f(M_{2})={\frac {PV_{s1}}{2\pi G}}}, где G -гравитационная постоянна, а f(M2) — функция масс звезды и по определению равна: f(M2)≡(M2sin(i))3(M1+M2)2{\displaystyle f(M_{2})\equiv {\frac {(M_{2}sin(i))^{3}}{(M_{1}+M_{2})^{2}}}}. В случае, если орбита не круговая, а имеет эксцентриситет, то можно показать, что для функции масса орбитальный период P должен быть домножен на фактор (1−e2)3/2{\displaystyle (1-e^{2})^{3/2}}. Если второй компонент не наблюдается, то функция f(M2) служит нижним пределом его массы. Стоит отметить, что изучая только кривые лучевых скоростей невозможно определить все параметры двойной системы, всегда будет присутствовать неопределённость в виде неизвестного угла наклонения орбиты[2]. Практически всегда гравитационное взаимодействие между двумя звёздами описывается с достаточной точностью законами Ньютона и законами Кеплера, являющимися следствием законов Ньютона. Но для описания двойных пульсаров (см. пульсар Тейлора-Халса) приходится привлекать ОТО. Изучая наблюдательные проявления релятивистских эффектов, можно ещё раз проверить точность теории относительности. Третий закон Кеплера связывает период обращения с расстоянием между компонентами и массой системы: где P{\displaystyle P} — период обращения, a{\displaystyle a} — большая полуось системы, M1{\displaystyle M_{1}} и M2{\displaystyle M_{2}} — массы компонентов, G{\displaystyle G} — гравитационная постоянная. Для визуально-двойной системы есть возможность определить орбиты обоих компонентов, рассчитать период и полуось, а также отношение масс. Но часто о двойственности системы можно судить только по спектральным данным (спектрально-двойные). По движению спектральных линий можно определить лучевые скорости одного компонента, а в редких случаях и сразу двух компонентов. Если известна лучевая скорость только одного компонента, то полную информацию о массах получить нельзя, но можно построить функцию масс и определить верхнюю границу массы второго компонента, а значит сказать, может ли он являться чёрной дырой или нейтронной звездой. Первым выдвинул идею о существовании двойных звёзд Джон Мичелл (Reverend John Michell). На выступлении в Королевском обществе в 1767 году он предположил, что многие звезды, видимые как двойные, действительно могут быть физически связаны. Наблюдательные подтверждения этой гипотезы были опубликованы сэром Уильямом Гершелем в 1802[13]. wikiredia.ru Звезды двойной системы 168 Зонная пластинка 212
[c.348] В выпрямителях применяются трансформаторы специального назначения, так как эти источники тока имеют такие характерные особенности, как неодновременная нагрузка различных фаз в соответствии с неодновременным прохождением тока через вентили блока выпрямителей. Как правило, обмотки трехфазных трансформаторов соединяют следующим образом звезда — две обратные звезды с уравнительным реактором звезда — звезда звезда—двойной зигзаг треугольник — звезда. К. п. д. трансформаторов источников тока для электрохимической обработки обычно несколько меньше, а масса несколько больше, чем трансформаторов обычного типа.
[c.177] Регулирование частоты вращения вала переключением числа пар полюсов. Из формулы (71) вытекает, что частота вращения вала асинхронного двигателя обратно пропорциональна числу пар полюсов. В данном случае возможно только ступенчатое регулирование частоты вращения вала двигателя. Число пар полюсов изменяют переключением каждой фазы обмотки двигателя с последовательного на параллельное соединение (рис. 21). На практике используют две схемы переключения 1) звезда — двойная звезда (рис. 21, а) и
[c.47] В том случае, когда можно измерить положения звезд относительно центра их масс, оказывается возможным определить отношение масс компонентов. Этот вид измерений требует весьма точного знания положений обеих звезд относительно далеких звезд фона за достаточно длительное время наблюдений. Продолжительные наблюдения одиночной звезды в течение многих лет показывают, что она имеет собственное движение относительно звезд фона, причем ее путь является отрезком дуги большого круга на небесной сфере. Однако если изучаемая звезда — двойная, то по дуге большого круга перемещается центр масс системы. Две звезды, образующие систему, движутся по кривым со слабыми колебаниями относительно центра масс (рис. 14.3). На
[c.449] Наблюдения над двойными звездами показывают, что звезда-спутник движется около главной звезды по эллипсу, в фокусе которого находится главная звезда, следовательно, здесь имеет место ньютонов закон притяжения. Если бы имел место закон притяжения пропорционально расстоянию, то главная звезда находилась бы в центре орбиты спутника, что противоречит наблюдениям.
[c.390] Уточненный третий закон Кеплера играет существенную роль в познании Вселенной, ибо при помощи него можно определить массы планет. Солнца и двойных звезд.
[c.155] В пользу того, что скорость света не зависит от скорости источника, говорят и некоторые астрономические наблюдения (например, над двойными звездами), а также другие опыты, поставленные позднее специально с целью проверки этого факта.
[c.176] Исключение — двойные звезды.
[c.80] Рассмотрим теперь задачу Кеплера требуется найти орбиты двух тел, силы взаимодействия между которыми определяются законом обратных квадратов. Классическим примером объекта для этой задачи является движение планет Солнечной системы. Другие важные примеры — это движение спутников вокруг планет и относительное движение компонентов двойной звезды. Уравнение движения F = М для i-й материальной точки из системы N таких точек имеет следующий вид
[c.280] Майкельсон применил интерферометрическое наблюдение для оценки малых угловых расстояний между двойными звездами, а также для оценки углового диаметра звезд. Метод Майкельсона, равно как и применение его к определению размеров субмикроскопических частичек, будет изложен ниже (см. 45). Наконец, понятно, что интерференционные методы, позволяющие с огромной точностью определять длину волны, могут служить для самых тонких спектроскопических исследований (тонкая структура спектральных линий, исследование формы и ширины спектральных линий, ничтожные изменения в строении спектральных линий). Интерференционные спектроскопы, их достоинства и недостатки будут обсуждены вместе с другими спектральными приборами (дифракционная решетка, призма) в 50.
[c.149] Указанным методом Майкельсон в начале 1920 г. измерил угловое расстояние между компонентами двойной звезды Капеллы, оказавшееся равным 0,042". При помощи этого прибора можно было даже проследить орбитальное движение звезд друг относительно друга, ибо в зависимости от положения звезд должны быть соответствующим образом ориентированы и щели на объективе.
[c.196] Двойные и кратные звезды. На 100 звездных систем приходится 30 одиночных звезд, 47 двойных систем
[c.1209] Симбиотические звезды [30] — тесные двойные системы, состоящие из холодной и горячей звезд. Хаотически изменяют свой блеск на 1—3 за время порядка года (иногда — десятков лет).
[c.1212] Двойные звезды. Закон тяготения, открытый Ньютоном, распространяется за пределы солнечной системы. В самом деле, весьма вероятно, что этот закон управляет движением двойных звезд. Вот что показывают наблюдения этих движений. Заметим, прежде всего, что наблюдения непосредственно дают нам не действительную орбиту звезды-спутника вокруг главной звезды, а проекцию этой орбиты на касательную плоскость к небесной сфере, т. е. на плоскость, проведенную через главную звезду Е перпендикулярно радиусу ТЕ, соединяющему Землю Т с этой звездой. Эта проекция и является видимой орбитой звезды-спутника. Наблюдения показывают, что
[c.343] То обстоятельство, что имеет место закон площадей для проекции движения на плоскость, проведенную через звезду Е перпендикулярно к радиусу ТЕ, соединяющему Землю со звездой, показывает (п. 208), что сила, действующая на звезду-спутник, постоянно пересекает прямую ТЕ. Так как это справедливо для всех двойных звезд и так как положение, занимаемое в пространстве Землей, никак не связано е двойными звездами, то естественно допустить, что сила, действующая на звезду-спутник, постоянно пересекает главную звезду Е. Так как сила центральная, то траектория будет плоско и так как ее проекция — эллипс, то она сама является эллипсом. В таком случае можно попытаться дать себе отчет и а природе силы, вызывающей это движение. Так как на каждую звезду-спутник действует сила, направленная к главной звезде и заставляющая звезду-спутник описывать эллипс, то закон этой силы, очевидно, таков, что движение спутника по коническому сечению, не зависит от того, каковы были начальные условия дви> е-ния спутника. Для нахождения этой силы необходимо решить следующую задачу.
[c.343] При первом законе, когда сила пропорциональна расстоянию, точка приложения будет описывать коническое сечение с центром в центре сил. Это не будет справедливым для двойных звезд, так как если центр действительной траектории звезды-спутника совпадает с главной звездой, то то же будет и для види.мой траектории.
[c.347] Четыре степени свободы. Двойная звезда, плоскость вращения которой не поворачивается.
[c.32] Для того чтобы почти круговая орбита была замкнутою или чтобы после одного обхода ее концы сходились, апсидальный угол должен содержаться в 2 тг четное число раз. Следовательно, значение от в (5) должно быть целым. Единственным случаем, при котором сила уменьшается с увеличением расстояния, будет случай, когда от = 1. Таким образом закон изменения силы обратно пропорционально квадрату расстояния является единственным законом, при котором невозмущенная орбита планеты, если она имеет конечные размеры, необходимо будет представлять овальную кривую. Этот вывод имеет практическое применение к случаю двойных звезд. При возможности произвести достаточное число наблюдений обнаруживалось, что относительная орбита каждой из двух компонент двойной звезды представляет овальную кривую, похожую на эллипс, хотя тело, к которому отнесено движение, может и не находиться в фокусе. Предыдущее замечание приводит к заключению, что закон тяготения имеет место- также и в этом случае, причем кажущееся отклонение центра силы от фокуса объясняется тем, что мы наблюдаем не истинную орбиту, которая наклонена к линии зрения, а ее проекцию на фоне неба.
[c.234] В астрономии этот случай осуществляется приблизительно всякий раз, когда рассматриваются такие два небесных тела, для которых можно пренебречь действиями на них всех остальных тел типичным примером являются так называемые двойные звезды.
[c.200] Допустим, что звезда двойная с угловым расстоянием между ее компонентами бф = 0/2. Тогда максимумы интерференционных полос от одной звезды наложатся на минимумы другой интер( ренционнйе полосы либо пропадут, либо их видимость сделается наименьшей. На этом основан интерференционный метод измерения угловых расстояний между компонентами двойных звезд, идея которого была предложена Физо. Надо менять расстояние между отверстиями 0 и 0 , пока не пропадут интерференционные полосы или их видимость сделается наименьшей. Если О — расстояние между отверстиями в этот момент, то угловое расстояние между компонентами двойной звезды найдется по формуле
[c.381] Недостатком способа Майкельсона является трудность расшифровки двойная звезда дает результаты, схожие с теми, которые получаются от звезды конечной ширины. Приходится допол1н1йТель-ными наблюдениями, например вращением зеркал Жз Ьколо оси трубы, выяснить, какая из двух возможностей правильна. Если звезда двойная, то при вращении диффракционная картина меняет вид например, когда зеркала расположены перпендикулярно линйи, соединяющей обе звезды, получается такая же картина, как в случае звезды без заметного диаметра.
[c.83] Э( фект Допилера был использован при определении лучевой скорости звезды (слагаю1ней скорости звезды вдоль линии, соединяющей звезду и Землю), для оценки скорости извержения водородных масс па Солнце, для измерения скорости вращения солнечного диска и т. д. Благодаря эффекту Допплера были открыты двойные звезды — звезды, обращающиеся вокруг общего центра тяжести.
[c.423] Орбитальное движение двойных звезд. Наиболее массивная звезда, известная в настоящее время — это звезда Дж. С. Пласкета. Она является двойной звездой ), т.е. состоит из двух звезд, связанных между собой силой тяготения. Из спектральных исследований известно
[c.296] На опыте заметного смещения интерференционных полос обнаружено не было. Смещения носили случайный характер и не превышали 0,02 полосы, что лежало в пределах ошибок наблюдений. Таким образом, опыты Майкельсона не подтвердили теорию неподвижного эфира. Они могли бы быть истолкованы, как доказательство полного увлечения эфира телами, но тогда они вступили бы в противоречие с результатами опыта Физо. Было предпринято несколько попыток объяснить отрицательный результат опытов Майкельсона, не отказываясь при этом от представлений о мировом эфире. Одной из них была баллистическая гипотеза Ритца, согласно которой к скорости светового луча, испускаемого движущимся источником, добавляется скорость самого источника, подобно тому, как к скорости снаряда, выпущенного из пушки движущегося корабля, добавляется скорость самого корабля. Однако баллистическая теория была отвергнута, так как она встретилась с неразрешимыми трудностями при объяснении опытов типа Физо, эффекта Доплера и результатов наблюдений за двойными звездами.
[c.209] Переменные звезды. Кроме эатменных переменных звезд, которые представляют собой двойные системы, изменяющие свой блеск вследствие периодических затмений одного компонента другим, имеются различные типы физических переменных звезд. Среди них наиболее многочисленны пульсирующие звезды (табл. 45.17).
[c.1209] Компактные звезды, входящие в состав тесных двойных систем, могут проявлять себя как рентгеновские источники [33]. Источником энергии служит аккреция вещества, перетекающего с нормальной звезды на компактную. Светимость аккрецирующих источников L,
[c.1213] Транзиентные (новоподобные) источники — системы, в которых аккреция происходит не постоянно в результате источник то появляется, то исчезает с интервалом от нескольких месяцев до нескольких лет. Это может быть связано с эллиптичностью орбиты релятивистской звезды в двойной системе или с пульсациями нормальной звезды, что приводит к сильным колебаниям скорости аккреции. Среди транзиентных источников есть рентгеновские пульсары и барстеры.
[c.1214] mash-xxl.infoЭнциклопедия по машиностроению XXL. Звезда двойная звезда схема
Регулирование скорости изменением числа пар полюсов - Help for engineer
Регулирование скорости изменением числа пар полюсов








Добавить комментарий
Звезды двойные - Справочник химика 21
В ряде случаев вместо переключения двойная звезда — треугольник применяют переключение звезда — двойная звезда . Общее построение схемы сохраняется. Более подробные сведения об этом приведены в специальной литературе [6]. [c.33]Двойные звезды

Общие сведения


Классификация
Материалы по теме

Явления и феномены, связанные с двойными звездами
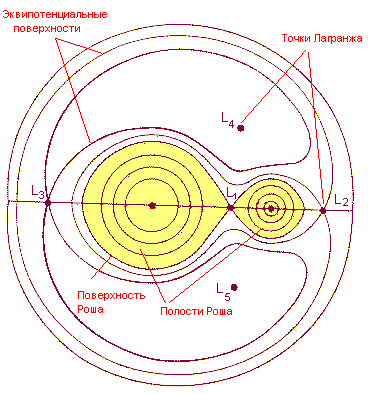
Происхождение и эволюция двойных звезд
Экзопланеты вокруг двойных звезд

Анализ и исследование двойных звезд

Интересные факты

Двойная звезда — WiKi
Эволюция тесной двойной системы в представлении художника Двойная система из О-звёзд в представлении художника Классификация
Визуально-двойные звёзды
Спекл-интерферометрические двойные звезды
Астрометрические двойные звёзды
Поведение астрометрическо-двойной на небе. Спектрально-двойные звёзды
Условный пример раздвоения и смещения линий в спектрах спектрально-двойных звёзд. Затменно-двойные звёзды
Микролинзированные двойные
Явления и феномены, связанные с двойными звёздами
Парадокс Алголя
Обмен массами между звёздами
Сечение поверхностей равного потенциала в модели Роша в орбитальной плоскости двойной системы Новые
Рентгеновские двойные
Симбиотические звёзды
Барстеры
Сверхновые типа Ia
Происхождение и эволюция
Теории с промежуточным ядром
Теории с промежуточным диском
Динамические теории
Экзопланеты в двойных системах
Экзопланета, находящаяся в двойной системе Kepler-47, в представлении художника Важные особенности процессов формирования
Планетезимальный сценарий образования
Несовместные сценарии образования
Астрономические данные и их анализ
Кривые блеска
Примеры кривых блеска для разделённой и тесной двойной системы Кривые лучевых скоростей
Определение масс компонентов
История открытия и изучения
См. также
Примечания
Литература
Ссылки
Двойная звезда Флексикуб по схеме Девида Бриля (David Brill)


 Приветствую Вас на сайте planetaorigami.ru. Меня зовут Анастасия, мне 27 лет и живу я в очень красивом городе Донецке.
Оцените статью: Поделитесь с друзьями! comments powered by HyperComments
Приветствую Вас на сайте planetaorigami.ru. Меня зовут Анастасия, мне 27 лет и живу я в очень красивом городе Донецке.
Оцените статью: Поделитесь с друзьями! comments powered by HyperComments Двойная звезда Википедия
Эволюция тесной двойной системы в представлении художника Двойная система из О-звёзд в представлении художника Классификация
Визуально-двойные звёзды
Спекл-интерферометрические двойные звезды
Астрометрические двойные звёзды
Поведение астрометрическо-двойной на небе. Спектрально-двойные звёзды
Условный пример раздвоения и смещения линий в спектрах спектрально-двойных звёзд. Затменно-двойные звёзды
Микролинзированные двойные
Явления и феномены, связанные с двойными звёздами
Парадокс Алголя
Обмен массами между звёздами
Сечение поверхностей равного потенциала в модели Роша в орбитальной плоскости двойной системы Новые
Рентгеновские двойные
Симбиотические звёзды
Барстеры
Сверхновые типа Ia
Происхождение и эволюция
Теории с промежуточным ядром
Теории с промежуточным диском
Динамические теории
Экзопланеты в двойных системах
Экзопланета, находящаяся в двойной системе Kepler-47, в представлении художника Важные особенности процессов формирования
Планетезимальный сценарий образования
Несовместные сценарии образования
Астрономические данные и их анализ
Кривые блеска
Примеры кривых блеска для разделённой и тесной двойной системы Кривые лучевых скоростей
Определение масс компонентов
История открытия и изучения
См. также
Примечания
Литература
Ссылки
Звезда двойная - Энциклопедия по машиностроению XXL
Одним из галактических источников, от к-рых ожидается регистрируемый поток Н. высоких энергий, является тесная двойная система Лебедь Х-3 (см. Гамма-астрономия). От этого источника зарегистрировано переменное гамма-излучение высокой ( 10 ГэВ) и сверхвысокой (---Ю — 107 ГэВ) энергии, с периодом 4,8 ч. Предполагается, что гамма-излучение генерируется в результате взаимодействия ускоренных протонов с макс, энергиями до 10 — 10 ГэВ с атомными ядрами газа, окружающего массивную звезду двойной системы. Этот процесс сопровождается генерацией Н. высоких энергий. Мин. нейтринный поток, совместимый в рамках описываемой модели с наблюдаемым потоком гамма-излучения, должен быть зарегистрирован проектируемыми установками Байкал (СССР) и Д ЮМ АНД (США).
[c.257]
Если размеры звезд двойной системы много меньше расстояния между ними, то звезды можно считать точечными источниками и рассматривать интерференционную картину от двух точечных источников, находящихся на расстоянии 2uo Друг от друга, т. е. на расстоянии между звездами двойной системы (рис. 120). Распределение яркости излучателя дается формулой
[c.168]
Таким образом, наблюдаемое движение звезды может заметно отступать от законов Кеплера. В частности, при очень большом L возможно, что даже при ц баллистической гипотезы противоречит наблюдению и, следовательно, гипотеза Ритца должна быть оставлена.
[c.452]Световая волна в вакууме представляет собой переменное электромагнитное поле высокой частоты, распространяющееся с постоянной скоростью (с = 2,9979-10 см/с), не зависящей от частоты. Последнее обстоятельство может считаться установленным с большой степенью достоверности наблюдениями над астрономическими явлениями. Так, исследование затмения удаленных двойных звезд не обнаруживает никаких аномалий в спектральном составе света, доходянщго до нас в начале н конце затмений. Между тем затмение звезды или выход ее из тени своего спутника означает обрыв или начало распространения светового импульса, далеко не монохроматического и могущего рассматриваться как результат наложения многих монохроматических излучений. Если бы скорость этих излучений в межпланетном пространстве была различна, то импульс должен был бы дойти до нас значительно деформированным. Например, предположим для простоты, что этот импульс можно уподобить двум почти монохроматическим группам, синей и красной , и примем, что скорость распространения красной группы больше, чем синей мы должны были бы наблюдать при начале затмения изменение цвета звезды от нормального к синему, а при окончании его — от красного к нормальному. При огромных расстояниях, отделяющих от нас двойные звезды, даже ничтожная разница в скоростях должна была бы дать заметный эффект. В действительности же такой эффект не имеет места. Так, наблюдения Aparo над переменной звездой Алголь привели его к заключению, что разность между скоростью распространения красного и фиолетового излучения во всяком случае меньше одной стотысячной величины самой скорости. Эти и подобные наблюдения заставляют признать, что дисперсия света в межпланетном пространстве ) отсутствует. При
[c.538] Рис. 10.26. Две спектрограммы двойной звезды а Близнецов, снятые в различные моменты времени. Только одна из двух звезд этой системы излучает свет, достаточно интенсивный для наблюдения. Заметьте, что линии спектра звезды сдвинуты относительно линий контрольного спектра, полученного в лаборатория, в различных направлениях соответственно двум стадиям движения звезды. В первой стаднн звезда движется по направлению к Земле, и частота света возрастает во второй стадии звезда удаляется от Земли, и частота уменьшается. /, —контрольные спектры, полученные в лаборатории 2 — звезда приближается 3 — звезда удаляется.

интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''

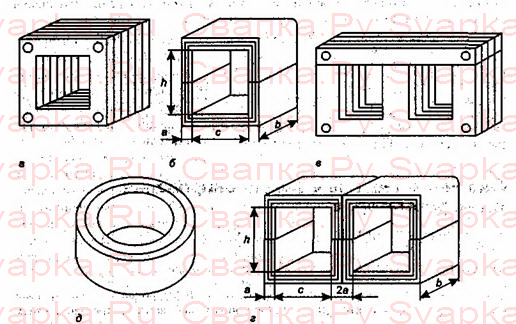











Поделиться с друзьями: