Фильтры более высокого качества реализуются на основе катушек индуктивности и конденсаторов. В LC-фильтр могут входить также и резисторы. Связь входной и выходной цепей большинства LC-фильтров соответственно с источником сигнала и с нагрузкой производится таким образом, чтобы значения их реактивных или полных сопротивлений были равны. На рис. 4 приведена схема и амплитудно-частотная характеристика типового Г - образного LC-фильтра нижних частот. Рис. 4. Схема и АЧХ Г - образного низкочастотного фильтра. Расчет такого фильтра производится по следующим формулам: Все LC-фильтры обладают тем преимуществом, что на переменном токе конденсаторы и катушки индуктивности работают взаимообратно, т.е. при увеличении частоты сигнала индуктивное сопротивление возрастает, а емкостное падает. Таким образом, в LC-фильтре нижних частот реактивное сопротивление параллельного элемента при увеличении частоты сигнала уменьшается и этот элемент шунтирует высокочастотные сигналы. На низких частотах реактивное сопротивление параллельного элемента достаточно высокое. Последовательный элемент обеспечивает прохождение низкочастотных сигналов, а для сигналов высоких частот его реактивное сопротивление велико. Простой Г - образный фильтр не обеспечивает достаточную крутизну амплитудно-частотной характеристики. Для увеличения крутизны в основную Г-образную структуру вводят дополнительную катушку индуктивности, как показано на рис. 5. Такой фильтр называется Т-образным. Рис. 5. Т - образный НЧ LC-фильтр. В Т - образном фильтре значение конденсатора С такое же, как и в исходной Г-образной структуре, и все ее расчетные формулы сохраняются. Суммарная индуктивность катушек L1 и L2 должна быть эквивалентна индуктивности единственной катушки исходной Г-образной структуры. Обычно требуемая общая индуктивность распределяется между двумя этими катушками поровну таким образом, чтобы каждая из катушек в Т - образном фильтре нижних частот имела индуктивность в два раза меньше, чем катушка в Г - образном фильтре. Крутизну амплитудно-частотной характеристики можно увеличить также путем введения в цепь дополнительного конденсатора. Такой фильтр называется П-образным (рис. 6.). Рис. 6. П-образный низкочастотный LC-фильтр. В П - образном фильтре значение индуктивности L такое же, как и в исходной Г-образной структуре, тогда как суммарная емкость конденсаторов С1 и С2 должна быть эквивалентна емкости конденсатора исходной Г - образной структуры. Обычно требуемая общая емкость распределяется между двумя этими конденсаторами поровну таким образом, чтобы каждый из конденсаторов в П - образном фильтре имел емкость, равную половине емкости конденсатора в Г - образном фильтре. На рис. 7 приведена схема и амплитудно-частотная характеристика типового Г - образногоLС-фильтра верхних частот. Рис. 7. Схема и АЧХ высокочастотного Г-образного LC-фильтра. Расчет Г - образного LС-фильтра верхних частот производится по следующим формулам: В этом фильтре при увеличении частоты сопротивление последовательного элемента уменьшается. Он пропускает высокочастотные сигналы, а для сигналов низких частот его реактивное сопротивление велико. Параллельный элемент оказывает шунтирующее влияние на сигналы низких частот, а для высокочастотных сигналов его реактивное сопротивление велико. Для увеличения крутизны амплитудно-частотной характеристики в Г - образную структуру можно ввести дополнительный конденсатор, как показано на рис. 8. Рис. 8. Т - образный высокочастотный LC-фильтр. Такой фильтр имеет Т - образную структуру. В Т - образном фильтре значение индуктивности L не отличается от ее значения в исходной Г - образной структуре и все расчетные формулы остаются такими же. Суммарная емкость конденсаторов С1 и С2 должна быть эквивалентна емкости одиночного конденсатора исходной Г-образной структуры. Обычно эта требуемая общая емкость распределяется поровну между двумя конденсаторами так, что Т - образном фильтре верхних частот каждый конденсатор имеет емкость, равную удвоенному значению емкости в Г - образной структуре. Крутизну амплитудно-частотной характеристики фильтра можно также повысить путем введения в схему дополнительной катушки индуктивности, как показано на рис. 9, образуя П - образный фильтр. Рис. 9. П-образный высокочастотный LC-фильтр. В П - образном LC-фильтре значение емкости конденсатора не изменяется, а суммарная индуктивность катушек L1 и L2 должна быть эквивалентна индуктивности одиночной катушки исходной Г-образной структуры. Обычно требуемая общая индуктивность распределяется поровну между двумя катушками так, что каждая из них имеет индуктивность, равную удвоенному значению индуктивности Г - образной структуры. Работа полосно-заграждающего (режекторного) фильтра основана на различии зависимостей полных сопротивлений параллельной и последовательной резонансных цепей от частоты. Полное сопротивление параллельной LC-цепи на резонансной частоте максимально, тогда как у последовательной цепи оно минимально. Эти две LC-цепи, соединенные определенным образом (рис. 10), образуют Г - образный режекторный фильтр. Рис. 10. Г - образный режекторный LC-фильтр. На центральной частоте требуемого диапазона полное сопротивление последовательной LC-цепи (она включена параллельно нагрузке) минимально, и она оказывает шунтирующее воздействие и ослабляет сигналы. Полное сопротивление параллельной LC-цепи (которая включена последовательно с нагрузкой) на центральной частоте требуемого диапазона максимально, и она препятствует прохождению сигналов. Т-образные и П-образные полосно-пропускающие фильтры (рис. 11) обладают более высокой крутизной амплитудно-частотной характеристики. Расчет полосно-пропускающих LC-фильтров производится по следующим формулам: Рис.11. Полосовые П- и Т-образные LC – фильтры. studfiles.net Практический расчет фильтров верхних и нижних частот (RC и LC фильтров) Доброго дня уважаемые радиолюбители! Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров верхних и нижних частот. В первую очередь определимся, что понятия “верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике. Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и служат для разных целей. Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный. Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель. АЧХ фильтра показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала.Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала. Тут же появляется еще одно определение: частота среза. Частота среза – это частота, на которой происходит спад амплитуды выходного сигнала до значения равного 0,7 от входного.Например, если при частоте входного сигнала 1 кГц амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра. И последнее определение – крутизна частотной характеристики фильтра. Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше. Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах. Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется реактивным и обозначается как Х. Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле: Xc=1/2пFС где:Хс – реактивное сопротивление конденсатора;п – оно и в Африке “пи”;F – частота;С – емкость конденсатора.То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты. А реактивное сопротивление катушки индуктивности вот этой формулой: XL=2пFL где:XL – реактивное сопротивление катушки индуктивности;п – оно и в России “пи”;F – частота сигнала;L – индуктивность катушки Частотные фильтры бывают нескольких типов:– одноэлементные;– Г- образные;– Т – образные;– П – образные;– многозвенные. В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем). - фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот). Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений: С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.Формулы для расчета параметров делителя напряжения: Uвх=Uвых*(R1+R2)/R2Uвых=Uвх*R2/(R1+R2)Rобщ=R1+R2R1=Uвх*R2/Uвых – R2R2=Uвых*Rобщ/Uвх К примеру, нам дано:Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 ВПорядок расчета:1. Определяем R2= 7*10000/10= 7000= 7 кОм2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм3. Проверяем Uвых=10*7000/(3000+7000)= 7 ВЧто нам и требовалось.Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже. ВАЖНО!Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.Это правило также справедливо и при расчетах фильтров. Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор. Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально. При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот.А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот. Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей. В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора. Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц. Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).Проводим расчет:1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.2. Определяем по формуле делителя напряжения сопротивление R2:R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.3. Определяем сопротивление резистора R1:R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1:C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.? Для справки:? 1 мкФ = 10-6 Ф = 0,000 001 Ф ? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф ? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф и так далее… Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц. Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).Проводим расчет:1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.2. Определяем по формуле делителя напряжения сопротивление R2:R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.3. Определяем сопротивление резистора R1:R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2:C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ. Т – образный фильтр Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза: П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза. Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов. Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо. radio-stv.ru Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и подавляют все остальные частоты. Частота, на которой начинается подавление, называется частотой среза fс (рис.28.1). Рис. 28.1. Частотная характеристика фильтра нижних (а) и верхних (б) частот. Влияние фильтра на прямоугольный сигнал Как уже говорилось в гл. 3, прямоугольный сигнал представляет собой сложное колебание, состоящее из основной гармоники и бесконечного количества нечетных гармоник. Низкочастотные составляющие формируют основание и плоскую вершину импульса, а высокочастотные — его фронт и срез. Когда прямоугольный сигнал проходит через фильтр, его форма искажается. Фильтр нижних частот (ФНЧ) будет искажать главным образом Фронты и срезы, делая их менее крутыми и скругляя углы, как показано на рис. 28.7(б). ФНЧ оказывает на прямоугольный сигнал такое же Действие, как усилители с недостаточной шириной полосы пропускания. Фильтр верхних частот (ФВЧ), наоборот, искажает плоскую вершину и снование прямоугольного сигнала (рис. 28.5(б)). RC- фильтры Простейшим среди фильтров является RC-фильтр. Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным. На схеме рис. 28.2 конденсатор соединен последовательно с резистором. При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падение напряжения Vc на конденсаторе будет большим, а на резисторе Vr — малым. При подаче на вход этого фильтра высокочастотного сигнала картина будет обратная: Vc будет малым, а Vr — большим. Если теперь представить эту схему, как на рис. 28.3(б), где падение напряжения на конденсаторе является выходным, то в выходном сигнале будут преобладать НЧ-составляющие, а высокочастотные будут сильно ослабляться. Другими словами, мы получили фильтр нижних частот. И наоборот, если выходное напряжение снимать с резистора (рис. 28.3(а)), то получим фильтр верхних частот. Значения R и С определяют частоту среза фильтра. Дифференциатор Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пички». На рис. 28.4 изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает ВЧ-составляющие входного сигнала, образующие фронт импульса АВ, а затем начинает заряжаться до 10 В. Если постоянная времени (произведение RC) мала в сравнении с периодом входных импульсов, конденсатор успеет полностью зарядиться до 10 В, прежде чем придет следующая ВЧ-составляющая импульса — срез CD (рис. 28.5(а)). Когда конденсатор полностью зарядится, ток прекращается и падение напряжения на резисторе, т. е. на выходе, равно нулю. Срез CD представляет собой перепад напряжения 10 В и состоит из ВЧ-компонент. Поэтому он свободно пройдет через конденсатор и напряжение на выходе скачком упадет до –10 В. После этого конденсатор начнет перезаряжаться до –10 В, и, если постоянная времени мала, он успеет полностью зарядиться до этого напряжения. При этом выходное напряжение спадет до нуля и будет оставаться таким до прихода следующего фронта и т. д. Если постоянная времени больше, чем период входных импульсов, то выходной сигнал будет иметь форму, как на рис. 28.5(б). Рис. 28.4. RC-дифференциатор. Рис. 28.5. Сигнал на выходе дифференциатора, изображенного на рис. 28.4, при малой (а) и большой (б) постоянной времени. Интегрирующая RC-цепъ Интегрирующая RC-цепь (интегратор) является фильтром нижних частот (ФНЧ) и при подаче на его вход прямоугольного сигнала выдает на выходе сигнал треугольной (пилообразной) формы. На рис. 28.6 изображен RC-интегратор. При подаче на его вход фронта прямоугольного импульса (рис. 28.7) конденсатор начинает заряжаться до напряжения +10 В. Еслизадать постоянную времени RC, большую в сравнении с периодом входного сигнала, то срез CD импульса поступит прежде, чем конденсатор успеет полностью зарядиться (рис. 28.7(а)). После этого конденсатор начинает заряжаться в обратном направлении. И опять в связи с большой постоянной времени фронт FE следующего импульса придет прежде, чем конденсатор успеет полностью зарядиться в отрицательном направлении и т.д. В результате на выходе получается сигнал треугольной формы, амплитуда которого меньше, чем амплитуда входного сигнала. Если постоянная времени мала в сравнении с периодом входного сигнала, то выходной сигнал будет иметь вид, как на рис. 28.7(б). Обратите внимание, что и в интеграторе, и в дифференциаторе постоянная времени всегда сравнивается с периодом входного сигнала. Например, постоянная времени 100 мкс является большой по сравнению с периодом, скажем, 5 мкс (частота входного сигнала 200 кГц), но малой в сравнении с периодом 5 мс (частота входного сигнала 200 Гц). Влияние RC-цети на синусоидальный сигнал Синусоидальный сигнал является простым гармоническим колебанием и не содержит высших гармоник, поэтому при подаче такого сигнала на фильтр любого типа его форма не изменяется. Амплитуда выходного синусоидального сигнала может уменьшиться в зависимости от того, находится его частота в пределах полосы пропускания или нет. В первом случае синусоидальный сигнал претерпевает очень малое затухание, во втором случае затухание может быть очень большим. Воздействие RC-цепи на пилообразный сигнал Интегратор скругляет острые кромки пилообразного сигнала (рис. 28.8). Степень скругления определяется постоянной времени схемы. При очень большой постоянной времени выходной сигнал будет иметь вид, как на рис.28.8(б). Рис. 28.8. Влияние интегрирующей цепочки на форму пилообразного напряжения. Рис. 28.9. Влияние дифференцирующей цепочки на форму пилообразного напряжения. На рис. 28.9 показано воздействие дифференциатора на сигнал пилообразной формы. При очень малой постоянной времени выходной сигнал получается в виде импульсов (пичков) (рис. 28.9(б)). В этом видео рассказывается о полосовых фильтрах: Исследование ачх пассивных фильтров методические указания. Схема фильтра
1.3. Описание lc-фильтров
Расчет фильтров нижних и верхних частот
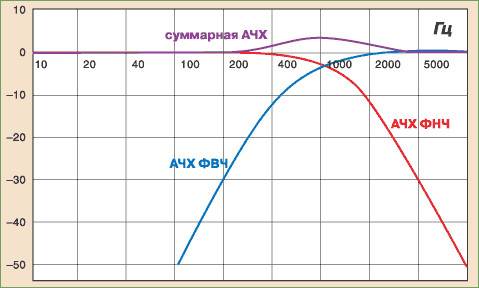Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).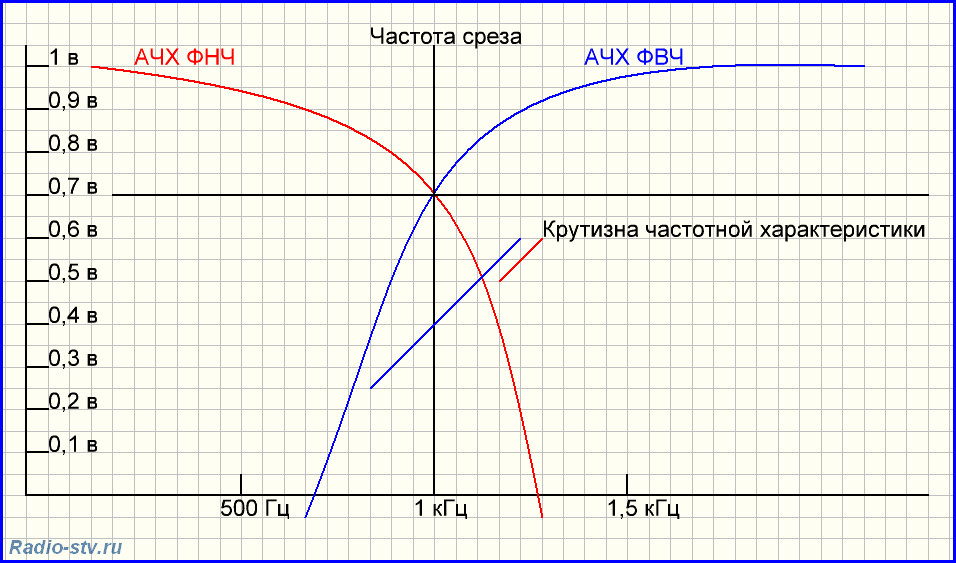
Одноэлементный фильтр
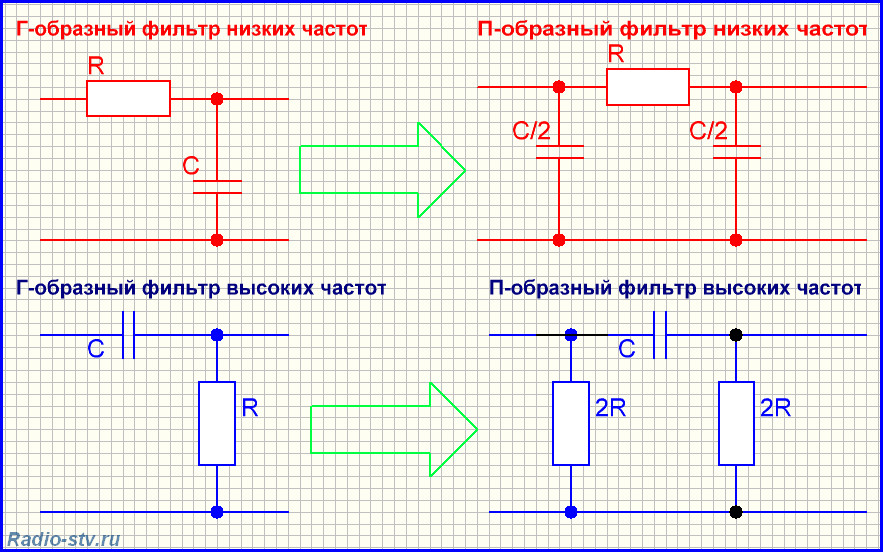
Г – образный фильтр
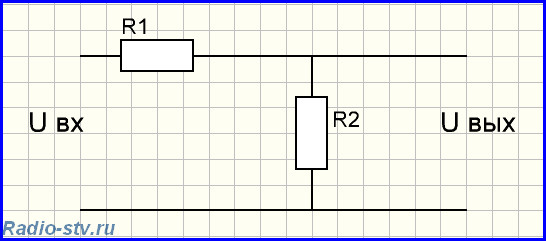
Порядок расчета Г-образного фильтра верхней частоты
Порядок расчета Г-образного фильтра нижней частоты
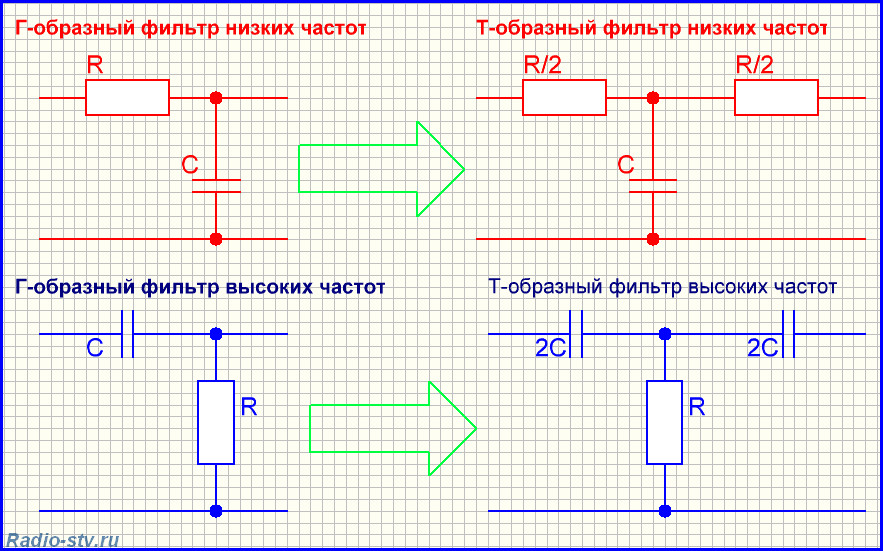
П – образный фильтр
RC-фильтры
Добавить комментарий
radiolubitel.net
Исследование ачх пассивных фильтров методические указания
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ТС
к лабораторной работе по дисциплине «Устройства приема и обработки радиосигналов в СПРС»
УФА. 2002
Составитель: А.И.Гулин
Исследование АЧХ пассивных фильтров с использованием математического пакета МАТLАВ: Методические указания к лабораторным работам по курсу «Устройства приема и обработки радиосигналов в системах подвижной радиосвязи» Уфимский государственный авиационный технический университет; составитель: А.И.Гулин. Уфа 2002, 13 с.
Рассмотрены основные характеристики фильтров различных аппроксимаций. Описано большинство видов пассивных фильтров, даны ориентировочные АЧХ фильтров первого и второго порядков.
Предназначены для студентов направления 201200 «Средства связи с подвижными объектами», а также могут быть полезны студентам других специальностей направления «Телекоммуникации».
Рецензент: Беспалов А. И.
Уфимский государственный авиационный технический университет, 2002.
Содержание
стр.
1. Теоретическая часть………………………………………………………………4
Назначение, классификация и принцип работы пассивных фильтров…….4
Описание RC-фильтров……………………………………………………….4
Описание LC-фильтров……………………………………………………….7
Сравнение пассивных фильтров с другими видами фильтров……………..9
Практическая часть………………………………………………………………11
Варианты заданий………………………………………………………………...12
Контрольные вопросы……………………………………………………………12
Список литературы……………………………………………………………….13
Теоретическая часть
1.1. Назначение, классификация и принцип работы пассивных фильтров.
Основное назначение фильтра состоит в том, чтобы исключить прохождение сигналов определенного диапазона частот и в то же время обеспечить передачу сигналов другого диапазона частот. Фильтры делятся на активные и пассивные. Активные фильтры представляют собой частотно-избирательный усилительный каскад. К пассивным фильтрам относятся RC- и LC-фильтры. Фильтры также можно классифицировать исходя из диапазона частот, которые они пропускают или подавляют. Существуют четыре типа фильтров:
1. Фильтр нижних частот, который пропускает все сигналы с частотой ниже некоторого заданного значения и подавляет сигналы более высоких частот.
2. Фильтр верхних частот, который пропускает все сигналы с частотой выше некоторого заданного значения и подавляет сигналы более низких частот.
3. Полосно-заграждающий фильтр (режекторный), который используется для подавления сигналов определенного диапазона частот, тогда как сигналы с частотами выше и ниже этого диапазона проходят беспрепятственно.
4. Полосно-пропускающий фильтр (полосовой), который пропускает сигналы заданной полосы частот и препятствует прохождению сигналов любых других частот.
1.2. Описание rc-фильтров.
Фильтрация сигналов низких (звуковых) частот обычно осуществляется с помощью фильтров на основе сопротивления и емкости (RC). Схема фильтра верхних частот и его амплитудно-частотная характеристика показаны на рис. 1.
Рис. 1. Схема и амплитудно-частотная характеристика высокочастотного RC-фильтра.
В этой схеме входное напряжение прикладывается и к резистору, и к конденсатору. Выходное же напряжение снимается с сопротивления. При уменьшении частоты сигнала возрастает реактивное сопротивление конденсатора, а следовательно, и полное сопротивление цепи. Поскольку входное напряжение остается постоянным, то ток, протекающий через цепь уменьшается. Таким образом, снижается и ток через активное сопротивление, что приводит к уменьшению падения напряжения на нем.
Фильтр характеризуется затуханием, выраженным в децибелах, которое он обеспечивает на заданной частоте. RC-фильтры рассчитываются таким образом, чтобы на выбранной частоте среза коэффициент передачи снижался приблизительно на 3 дБ (т.е. составлял 0,707 входного значения сигнала). Частота среза фильтра по уровню - 3 дБ определяется по формуле:
Фильтр низких частот имеет аналогичную структуру, только емкость и сопротивление там меняются местами. Амплитудно-частотную характеристику такого фильтра можно представить как зеркальное отображение АЧХ предыдущего.
В этой цепи входное напряжение также прикладывается и к резистору, и к конденсатору, но выходное напряжение снимается с конденсатора. При увеличении частоты сигнала реактивное сопротивление конденсатора, а следовательно, и полное сопротивление уменьшаются. Однако, поскольку это полное сопротивление состоит из реактивного и фиксированного активного сопротивлений, его значение уменьшается не так быстро, как реактивное сопротивление. Следовательно, при увеличении частоты снижение реактивного сопротивления (относительно полного сопротивления) приводит к уменьшению выходного напряжения. Частота среза этого фильтра по уровню -3 дБ также определяется по формуле предыдущего фильтра.
Рассмотренные выше фильтры представляют собой RC-цепи, которые характеризуются тремя параметрами, а именно: активным, реактивным и полным сопротивлениями. Обеспечиваемая этими RC-фильтрами величина затухания зависит от отношения активного или реактивного сопротивления к полному сопротивлению.
При расчете любого RC-фильтра можно задать номинал либо резистора, либо конденсатора и вычислить значение другого элемента фильтра на заданной частоте среза. При практических расчетах обычно задают номинал сопротивления, поскольку он выбирается на основании других требований. Например, сопротивление фильтра является его выходным или входным полным сопротивлением.
Соединяя фильтры верхних и нижних частот, можно создать полосовой RC-фильтр, схема и амплитудно-частотная характеристика которого приведены на рис. 2.
Рис. 2. Схема и АЧХ полосовогоRC-фильтра.
На схеме рис. 2.R1 - полное входное сопротивление; R2 - полное выходное сопротивление, а частоты низкочастотного и высокочастотного срезов определяются по формулам:
Следует отметить, что значение верхней частоты среза (fсв) должно быть по крайней мере быть в 10 раз больше нижней частоты среза (fсн), поскольку только в этом случае полосно-пропускающий фильтр будет работать достаточно эффективно.
Одиночный RC-фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области довольно часто используют многозвенные фильтры (рис. 3.). Частота среза многозвенного фильтра определяется по формуле ВЧ,НЧ RC-фильтра. Добавление каждого звена приводит к увеличению затухания на заданной частоте среза примерно на 6 дБ.
Рис. 3. Многозвенные фильтры: соответственно высокочастотный и низкочастотный.
studfiles.net
44. Электрические схемы фильтров Золотарева. Характеристики рабочего затухания фнч, фвч, пф Золотарева. Физический смысл работы фильтров
Имеют самую крутую характеристику в ПЗ. Чтобы получить схему ФНЧ Золотарёва надо взять схему ФНЧ Чебышева и подключить параллельно катушке L2конденсаторC2.
Выберем резонансную частоту этого контура в начале ПЗ и обозначим её . На этой частоте получается резонанс токов, и сопротивление идеального параллельного контура будет равно бесконечности. Ток частотычерез контура не пройдёт, значит. Характеристика вынуждена стремиться к, и она поэтому идёт круче.
На частотах выше сопротивление контура падает. Токи проходят через контур, иуменьшается. Получается провал характеристики, но он не может опускаться ниже.
Можно получить такую же характеристику, если во второй схеме последовательно с C2включить катушкуL2.
На частоте в контуреL2–C2наступает резонанс напряжений, и сопротивление идеального последовательного контура равно 0. Ток частотыпойдёт через контур, значитна нагрузке (т. е. ток частотыполностью закорачивается через контурL2–C2).
Контур, из-за которого получается всплеск характеристики, называется режекторным. Сколько в схеме режекторных контуров, столько будет всплесков характеристики. Нарисуем схему и характеристику ФВЧ Золотарёва 5-го порядка:
Чтобы получить ПФ Золотарёва, надо взять схему ФНЧ и ФВЧ Золотарёва, совместить их и сдвинуть вправо.
ФНЧ:
ФВЧ:
ПФ:
Контура L2а–C2аиL2б–C2бнастроены на частотыисоответственно.на этих частотах, т. к. в каждом контуре резонанс токов, получается всплеск характеристики.
На резонансной частоте сопротивление контураL2а–C2аносит емкостной характер, аL2а–C2а— индуктивный. Подбирают так эквивалентные емкостное и индуктивное сопротивление, чтобы на резонансной частотеони были равны. Значит между контурами возникает коллективный резонанс напряжений, и сопротивление всего участка стремится к 0, поэтому ток частотыf0легко пройдёт через этот участок в нагрузку. КонтураL1–C1иL3–C3настроены в резонанс на центральную частоту. Сопротивление этих контуров велико, и ток частотыf0через них не проходит, а пойдёт в нагрузку.
45. Активные фильтры. Особенности, принципиальные электрические схемы фильтров нижних и верхних частот. Понятие о расчете параметров фильтров
Фильтры, построенные на реактивных элементах L и C, имеют недостатки — большие габариты, вес и потери, поэтому разработаны электронные аналоги LC-фильтров, построенные на основе ОУ и элементов RC, т. е. безиндуктивные фильтры. Порядок фильтра определяется числом реактивных элементов. Основой ARC-фильтровявляется звено второго порядка. Для построения фильтров высших порядков используют каскадное соединение звеньев второго и первого порядка. В качествезвена первого порядкаиспользуют обычную пассивную RC-цепь.Звено второго порядка—НЧ ARC-фильтра:
ФНЧ
Токи частоты и токи НЧ легко проходят на вход ОУ черезR1иR2. Токи ВЧ замыкаются черезC2и возвращаются с выхода снова на вход ОУ через цепь ОС, не проходя в нагрузку.
Звено второго порядкаВЧ ARC-фильтра
ФВЧ
Токи частоты и токи ВЧ легко проходят на вход ОУ через конденсаторыC1иC2. Токи НЧ плохо проходят черезC1иC2, замыкаются черезR2и возвращаются с выхода ОУ снова на вход через цепь ОС, не попадая в нагрузку. ИзобразимARC-фильтр ВЧ четвёртого порядкапутём соединения двух звеньев второго порядка.
Расчёт ARC-фильтров — задача трудоёмкая и производится с помощью специальных таблиц фильтров Баттерворта для активных фильтров.
studfiles.net
Сглаживающие фильтры | HomeElectronics
Всем доброго времени суток. Сегодня продолжение темы про выпрямители и поговорим мы о сглаживающих фильтрах выпрямителей. Сглаживающие фильтры включаются между выпрямителем и нагрузкой для уменьшения переменных составляющих (пульсаций) выпрямленного напряжения. Эти фильтры выполняются из индуктивных элементов – дросселей и из ёмкостных элементов – конденсаторов. Простейший сглаживающий фильтр может состоять только из одного элемента, например дросселя или конденсатора. В малогабаритной аппаратуре сравнительно малой мощности индуктивные элементы фильтра могут быть заменены активными (резисторами).
Сглаживающие фильтры, прежде всего, характеризуются коэффициентом сглаживания q, представляющим собой отношение коэффициентов пульсаций на входе S0 и выходе S0H фильтра:
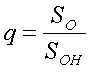
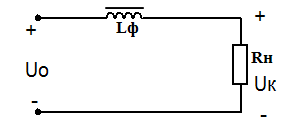
Индуктивный сглаживающий фильтр
Применяется в маломощных выпрямителях, но может входить в состав сложных многозвенных фильтров. Параметры дросселя следует выбирать так, чтобы активное сопротивление обмотки rдр было много меньше сопротивления нагрузки (rдр << Rн), а индуктивное сопротивление Xдр = 2πfпLф на частоте пульсаций fп – много больше, чем Rн(Xдр >> Rн). В этом случае почти вся постоянная составляющая напряжения будет приложена к нагрузке, а переменная составляющая – к дросселю.
По заданному коэффициенту сглаживания q можно рассчитать необходимую индуктивность сглаживающего фильтра
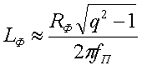
Индуктивный фильтр прост, дешев, имеет малые потери мощности; коэффициент сглаживания фильтра растёт с увеличением индуктивности дросселя, числа фаз питающего напряжения и с уменьшением сопротивления нагрузки. Поэтому индуктивные фильтры обычно применяются совместно с многофазными мощными выпрямителями. При отключении нагрузки или скачкообразном изменении ее сопротивления возможно возникновение перенапряжений; в этом случае параллельно обмотке дросселя необходимо включать защитные устройства, например разрядники. В маломощных однофазных выпрямителях индуктивный фильтр может являться звеном более сложного фильтра.
Eмкостной сглаживающий фильтр
Емкостной сглаживающий фильтр состоит из конденсатора Сф, подключённого параллельно сопротивлению нагрузки Rн. Принцип действия заключается в накоплении электрической энергии конденсатором фильтра и последующей отдачи этой энергии в нагрузку. Заряд и разряд конденсатора фильтра происходит с частотой пульсаций fп выпрямленного напряжения.
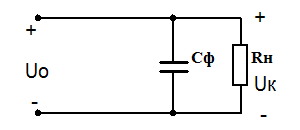
Для расчёта ёмкости конденсатора сглаживающего фильтра можно воспользоваться следующей формулой
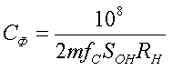, где
результируещее значение ёмкости выражено в микрофарадах,SOH – коэффициент пульсаций в процентах, %;RH – сопротивление нагрузки в омах, Ом;fc – частота сети в герцах, Гц;m – число используемых при выпрямлении полупериодов за период напряжения сети,m = 1 – для однополупериодных, m = 2 – для двухполупериодных.
Емкостной фильтр целесообразней всего применять совместно с однофазными и маломощными схемами выпрямления.
Сглаживающий LC фильтр
Сглаживание пульсаций выпрямленного напряжения будет более эффективным, если в совместить два предыдущих фильтра: индуктивный и емкостной фильтры. Данные типы сглаживающих фильтров называют LC фильтрами
Простейший Г-образный индуктивно-емкостный фильтр рассчитывают такким образом, чтобы параметры элементов подходили под следующие условия
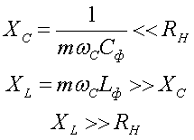
Коэффициент сглаживания Г-образного фильтра связан с произведением индуктивности и емкости следующим образом:
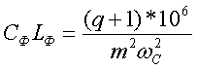
Сглаживающие RC фильтры
В схемах выпрямления малой мощности дроссель фильтра может быть заменён резистором RФ. Такие типы фильтров называют RC фильтрами
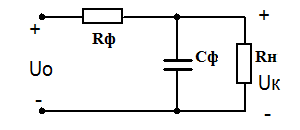
Расчёт сглаживающего RC фильтра должен вестись с учётом следующих условий
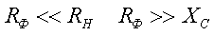
Коэффициент сглаживания фильтра
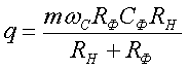
Сопротивление резистора RФ обычно задаются в пределах RФ = (0,15…0,5)RH; КПД резистивно-емкостного фильтра сравнительно мал и обычно составляет 0,6…0,8, причем при ηф = 0,8 RФ = 0,25RH. Емкость Cф (в микрофарадах), обеспечивает требуемый коэффициент сглаживания q при частоте сети fC = 50 Гц, находят из выражения
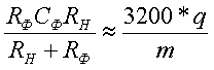
Преимущества резистивно-емкостных фильтров: малые габариты, масса и стоимость; недостаток – низкий КПД.
Многозвенные сглаживающие фильтры
Если с помощью индуктивно-емкостного фильтра необходимо обеспечить коэффициент сглаживания пульсаций более 40…50, то вместо однозвенного фильтра целесообразнее использовать двухзвенный сглаживающий фильтр.
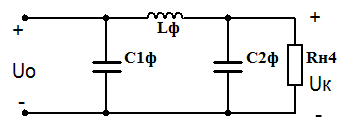
Фильтры с тремя и более звеньями на практике применяются редко. В общем случае коэффициент сглаживания многозвенного фильтра равен произведению коэффициентов сглаживания отдельных звеньев: q = q’q’’q’’’ …
Сглаживающие индуктивно-емкостные фильтры достаточно просты и эффективны в выпрямительных устройствах средней и большой мощностей. Однако масса и габариты таких фильтров весьма значительны, коэффициент сглаживания снижается с ростом тока нагрузки, фильтры малоэффективны при появлении медленных изменений сетевого напряжения. Индуктивные элементы фильтра являются источниками магнитных полей рассеяния, а совместно с паразитными емкостными элементами создают колебательные контуры, способствующие появлению переходных процессов.
Транзисторный сглаживающий фильтр
Транзисторные фильтры по сравнению с индуктивно-емкостными сглаживающими фильтрами имеют меньшие габариты, массу и более высокий коэффициент сглаживания пульсаций.
Фильтры могут быть выполнены по схемам с последовательным или параллельным включением силового транзистора по отношению к сопротивлению нагрузки, а также с включением нагрузки RH в цепь коллектора или эмиттера транзистора. Недостатком фильтров с нагрузкой в цепи коллектора является большое изменение выходного напряжения при изменении сопротивления нагрузки. Поэтому чаще используют фильтры, в которых сопротивление нагрузки включено в цепь эмиттера силового транзистора.
Фильтр с последовательным транзистором
Транзисторный сглаживающий фильтр с последовательным включением транзистора и нагрузкой в цепи эмиттера эквивалентен П-образному LC фильтру. Принцип действия его основан на том, что коллекторный и эмиттерный токи транзистора в режиме усиления практически не зависит от напряжения коллектор-эмиттер. Если выбрать рабочую точку транзистора на горизонтальном участке выходной вольт-амперной характеристики, то его сопротивление для переменного тока будет значительно большим, чем для постоянного тока.
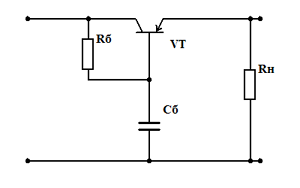Транзисторный фильтр
В схеме базовый ток транзистора VT задается резистором Rб. Конденсатор Сб достаточно большой емкости устраняет напряжение пульсаций на переходе эмиттер-база. Поэтому переменная составляющая напряжения пульсаций прикладывается к переходу база-коллектор и выделяется на транзисторе VT. В коллекторном и эмиттерном токе переменная составляющая практически отсутствует, поэтому пульсации в нагрузке RH также очень малы.
Коэффициент сглаживания транзисторного фильтра тем больше, чем больше коэффициент передачи тока транзистора VT и чем больше значение отношений
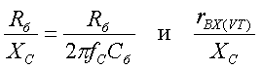
то есть чем меньше напряжение пульсаций на переходе эмиттер-база силового транзистора.
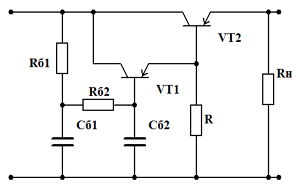Составной транзистор
Для более успешного выполнения этих соотношений конденсатор Сб может быть заменён одно- или двухзвенным RC сглаживающим фильтром, а для увеличения коэффициента передачи тока транзистор VT можно выполнить составным
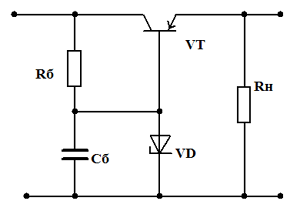Транзисторный фильтр со стабилитроном
Еще эффективней работает транзисторный фильтр, у которого в цепь базы транзистора включен стабилитрон
Коэффициент полезного действия транзисторного фильтра будет тем больше, чем меньше падание постоянного напряжения на силовом транзисторе. Однако амплитуда переменной составляющей напряжения на транзисторе не должна превышать значение постоянного напряжения на нём, иначе фильтр потеряет свою работоспособность.
Фильтр с параллельным транзистором
Фильтр с балластным резистором и параллельным включением транзистора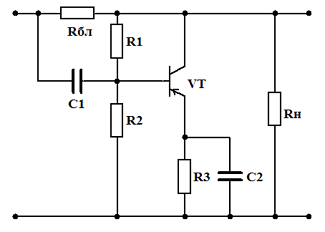 
Фильтр с балластным резистором и последовательным включением транзистора Транзисторные фильтры с балластным резистором Rбл и параллельным включением транзистора относительно нагрузки, в отличие от схем с последовательным включением, применяется при сравнительно небольшом выпрямленном напряжении (десятки вольт). Режим работы транзистора VT – минимальное значение тока IK.min – устанавливается соответствующим выбором сопротивлений R1 и R2. Переменная составляющая напряжения в этой схеме прикладывается к переходу эмиттер-база транзистора VT, усиливается и выделяется на балластном резисторе Rбл. Эта составляющая оказывается в противофазе с переменной составляющей напряжения, выделяющейся на Rбл при непосредственном протекании тока нагрузки. Выбором Rбл и IK.min можно добиться их полной компенсации. Амплитуда переменной составляющей тока транзистора VT должна быть меньше протекающего постоянного тока IK.min, иначе схема будет неработоспособна. Ток IK.min, не должен быть очень малым, так как иначе потребуется увеличение сопротивления Rбл, что приведёт к снижению КПД фильтра. Слишком большой ток также нецелесообразен, так как увеличивается мощность потерь на транзисторе и снижается КПД.
Коэффициент сглаживания параллельного транзисторного фильтра будет тем больше, чем больше сопротивление Rбл, емкость конденсаторов С1 и С2, крутизна вольт-амперной характеристики транзистора. Недостатком транзисторного фильтра с параллельным включением транзистора является значительное изменение среднего значения коллекторного тока транзистора, при изменении среднего значения выпрямленного напряжения, поступающего на вход фильтра. Это приводит к снижению КПД фильтра.
Следует помнить, что транзисторные фильтры не обеспечивают стабилизацию постоянной составляющей выпрямленного напряжения, а при изменении тока нагрузки, температуры окружающей среды и воздействия других дестабилизирующих факторов вносят дополнительную нестабильность выпрямленного напряжения.
Теория это хорошо, но теория без практики - это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками
Скажи спасибо автору нажми на кнопку социальной сети
www.electronicsblog.ru
Фильтры. Вновь. По порядку… | журнал АвтоЗвук
Профессиональный рецепт Огюста Родена наилучшим образом подходит для нашей темы. А тема была давно обещана читателям. Вновь (поскольку «вспомнить всё») разобраться с электрическими фильтрами во всех формах, в которых они применяются в нашей узкой отрасли.
…взять глыбу мрамора и отсечь от нее всё лишнее…Огюст Роден
Любой фильтр, в сущности, делает со спектром сигнала то же, что Роден с мрамором. Но в отличие от творчества скульптора замысел принадлежит не фильтру, а нам с вами.
Нам с вами по понятным причинам больше всего знакома одна сфера применения фильтров — разделение спектра звуковых сигналов для последующего воспроизведения их динамическими головками (нередко мы говорим «динамиками», но сегодня материал серьёзный, поэтому к терминам будем тоже подходить со всей строгостью). Но эта область использования фильтров, наверное, всё же не основная и совершенно точно, что не первая в историческом плане. Не будем забывать, что электроника когда-то называлась радиоэлектроникой, и первоначальной её задачей было обслуживание нужд радиопередачи и радиоприёма. И даже в те детские годы радио, когда сигналы сплошного спектра не передавались, а радиовещание ещё называлось радиотелеграфией, возникла потребность повышения помехозащищённости канала, и решена эта задача была за счёт использования фильтров в приёмных устройствах. На передающей стороне фильтры применялись для ограничения спектра модулированного сигнала, чем также удалось повысить надёжность передачи. В конце концов, краеугольный камень всей радиотехники тех времён, резонансный контур — не что иное, как частный случай полосового фильтра. Поэтому можно сказать, что вся радиотехника началась с фильтра.
Конечно, первые фильтры были пассивными, состояли они из катушек и конденсаторов, а с помощью резисторов удавалось получить нормированные характеристики. Но все они обладали общим недостатком — их характеристики зависели от импеданса той цепи, которая стоит за ними, то есть цепи нагрузки. В простейших случаях импеданс нагрузки можно было поддерживать достаточно высоким, чтобы этим влиянием можно было пренебречь, в других случаях взаимодействие фильтра и нагрузки приходилось учитывать (между прочим, расчёты зачастую велись даже без логарифмической линейки, просто в столбик). Избавиться от влияния импеданса нагрузки, этого проклятия пассивных фильтров, удалось с появлением активных фильтров.
Изначально предполагалось посвятить этот материал целиком и полностью пассивным фильтрам, их в практике инсталляторов приходится рассчитывать и изготавливать своими силами несравнимо чаще, чем активные. Но логика потребовала, чтобы мы всё же начали с активных. Как ни странно, потому что они проще, что бы ни казалось при первом взгляде на приводимые иллюстрации.
Хочу быть понятым верно: сведения об активных фильтрах не призваны служить исключительно руководством по их изготовлению, такая надобность появляется далеко не всегда. Гораздо чаще возникает нужда понять, как работают уже имеющиеся фильтры (главным образом — в составе усилителей) и почему они не всегда работают так, как нам бы хотелось. И здесь, действительно, может прийти мысль о ручной работе.
Принципиальные схемы активных фильтров
В простейшем случае активный фильтр представляет собой пассивный фильтр, нагруженный на элемент с единичным коэффициентом передачи и высоким входным импедансом — либо на эмиттерный повторитель, либо на операционный усилитель, работающий в режиме повторителя, то есть с единичным усилением. (Можно реализовать и катодный повторитель на лампе, но ламп я, с вашего позволения, касаться не буду, если кому интересно — обратитесь к соответствующей литературе). По идее, не возбраняется таким способом построить активный фильтр любого порядка. Поскольку токи во входных цепях повторителя очень малы, то, казалось бы, элементы фильтра могут быть выбраны очень компактными. Все ли? Представьте себе, что нагрузкой фильтра является резистор 100 Ом, вы хотите сделать фильтр НЧ первого порядка, состоящий из единственной катушки, на частоту 100 Гц. Каков должен быть номинал катушки? Ответ: 159 мГн. Какая уж тут компактность. И главное, что омическое сопротивление такой катушки может оказаться вполне сравнимым с нагрузкой (100 Ом). Поэтому о катушках индуктивности в схемах активных фильтров пришлось забыть, другого выхода просто не было.
Для фильтров первого порядка (рис. 1) я приведу два варианта схемной реализации активных фильтров — с ОУ и с эмиттерным повторителем на транзисторе n-p-n типа, а вы уж сами при случае выберете, с чем вам проще будет работать. Почему n-p-n? Потому, что их больше, и потому, что при прочих равных условиях в производстве они получаются несколько «лучше». Моделирование проводилось для транзистора КТ315Г — единственного, наверное, полупроводникового прибора, цена на который до последнего времени была точно такая же, как и четверть века назад — 40 копеек. Фактически вы можете использовать любой n-p-n транзистор, коэффициент усиления которого (h31э) не намного ниже 100.
Рис. 1. Фильтры ВЧ первого порядка
Резистор в цепи эмиттера (R1 на рис. 1) задаёт ток коллектора, для большинства транзисторов его рекомендуют выбирать примерно равным 1 мА или немного меньше. Частоту среза фильтра определяет ёмкость входного конденсатора C2 и общее сопротивление параллельно включённых резисторов R2 и R3. В нашем случае это сопротивление составляет 105 кОм. Надо только следить, чтобы оно было значительно меньше, нежели сопротивление в цепи эмиттера (R1), умноженное на показатель h31э — в нашем случае это примерно 1200 кОм (в действительности при разбросе значений h31э от 50 до 250 — от 600 кОм до 4 МОм). Выходной конденсатор добавлен, что называется, «для порядка» — если нагрузкой фильтра будет входной каскад усилителя, там, как правило, уже стоит конденсатор для развязки входа по постоянному напряжению.
В схеме фильтра на ОУ здесь (как и в последующем) использована модель TL082C, поскольку этот операционный усилитель очень часто применяется для построения фильтров. Впрочем, можно брать едва ли не любой ОУ из тех, что нормально работают с однополярным питанием, предпочтительнее с входом на полевых транзисторах. Здесь также частота среза определяется соотношением ёмкости входного конденсатора C2 и сопротивлением параллельно включённых резисторов R3, R4. (Почему параллельно включённых? Потому, что с точки зрения переменного тока плюс питания и минус — одно и то же.) Соотношение резисторов R3, R4 определяет среднюю точку, если они будут немного различаться, это не трагедия, это лишь означает, что сигнал максимальной амплитуды начнёт ограничиваться с одной стороны несколько раньше. Фильтр рассчитан на частоту среза 100 Гц. Чтобы её понизить, надо увеличить либо номинал резисторов R3, R4, либо емкость C2. То есть номинал изменяется обратно пропорционально первой степени частоты.
В схемах фильтра НЧ (рис. 2) на пару деталей больше, поскольку входной делитель напряжения не используется как элемент частотно-зависимой цепи и добавляется разделительная ёмкость. Для понижения частоты среза фильтра надо увеличивать входной резистор (R5).
Рис. 2. Фильтры НЧ первого порядка
Разделительная ёмкость имеет нешуточный номинал, так что без электролита обойтись будет трудно (хотя можно ограничиться плёночным конденсатором 4,7 мкФ). Следует учитывать, что разделительная ёмкость совместно с C2 образуют делитель, и чем она меньше, тем выше ослабление сигнала. Как следствие, несколько смещается и частота среза. В некоторых случаях можно обойтись без разделительного конденсатора — если, к примеру, источником является выход другого каскада фильтра. А вообще стремление избавиться от громоздких разделительных конденсаторов и явилось, наверное, основной причиной перехода от однополярного питания к двухполярному.
На рис. 3 и 4 показаны частотные характеристики фильтров ВЧ и НЧ, схемы которых мы только что рассмотрели.
Рис. 3. Характеристики фильтров ВЧ первого порядка
Рис. 4. Характеристики фильтров НЧ первого порядка
Весьма вероятно, что у вас уже возникли два вопроса. Первый: а что это мы так плотно занялись изучением фильтров первого порядка, когда для сабвуферов они не годятся вовсе, да и для разделения полос фронтальной акустики, если верить высказываниям автора, они применимы, мягко говоря, не часто? И второй: а почему автор не упомянул ни Баттерворта, ни его однофамильцев — Линквица, Бесселя, Чебышева, в конце концов? На первый вопрос я пока отвечать не буду, чуть позже вам всё станет ясно. Сразу перехожу ко второму. Баттервортом со товарищи были определены характеристики фильтров от второго порядка и выше, а частотная и фазовая характеристика фильтров первого порядка всегда одна и та же.
Итак, фильтры второго порядка, с номинальной крутизной спада 12 дБ/окт. Такие фильтры повсеместно делаются с использованием ОУ. Можно, конечно, обойтись и транзисторами, но для того, чтобы схема работала точно, приходится учитывать много всего, и в результате простота оказывается чисто мнимой. Известно энное количество вариантов схемной реализации таких фильтров. Я даже не скажу какое, поскольку любое перечисление всегда может оказаться неполным. Да и нам оно мало что даст, поскольку по-настоящему углубляться в теорию активных фильтров нам вряд ли имеет смысл. Тем более что в построении фильтров усилителей участвуют по большей части лишь две схемные реализации, можно даже сказать, что полторы. Начнём с той, которая «целая». Это так называемый фильтр Саллена — Ки (Sallen — Key).
Рис. 5. Фильтр ВЧ второго порядка
Здесь, как и всегда, частота среза определяется номиналами конденсаторов и резисторов, в данном случае — C1, C2, R3, R4, R5. Обратите внимание, для фильтра Баттерворта (ну наконец-то!) номинал резистора в цепи обратной связи (R5) должен быть вдвое меньше номинала резистора, включённого в «землю». Как обычно, в «землю» получаются включенными резисторы R3 и R4 параллельно, и суммарный номинал их 50 кОм.
Теперь несколько слов как бы в сторону. Если у вас фильтр не перестраиваемый, проблем с подбором резисторов не будет. Но если вам надо плавно менять частоту среза фильтра, нужно одновременно изменять два резистора (у нас их три, но в усилителях питание двухполярное, и там один резистор R3, номинала такого же, как наши два R3, R4, включённые параллельно). Специально для таких целей выпускаются сдвоенные переменные резисторы разного номинала, но они и дороже, и не так их много. Кроме того, можно разработать фильтр с очень близкими характеристиками, но у которого оба резистора будут одинаковыми, а ёмкости C1 и C2 — разными. Но это хлопотно. А теперь давайте посмотрим, что будет, если взять фильтр, рассчитанный на среднюю частоту (330 Гц) и начать менять лишь один резистор — тот, который в «землю». (Рис. 6).
Рис. 6. Перестройка фильтра ВЧ
Согласитесь, нечто подобное мы многократно видели на графиках в тестах усилителей.
Схема фильтра НЧ похожа на зеркальное отображение фильтра ВЧ: в обратной связи стоит конденсатор, а в горизонтальной полке буквы «Т» — резисторы. (Рис. 7).
Рис. 7. Фильтр НЧ второго порядка
Как и в случае с фильтром НЧ первого порядка, добавляется разделительный конденсатор (C3). Величина резисторов в цепи создания локальной «земли» (R3, R4) влияет на величину затухания, вносимого фильтром. При указанном на схеме номинале аттенюация около 1,3 дБ, думаю, с этим можно мириться. Как всегда, частота среза обратно пропорциональна номиналу резисторов (R5, R6). Для фильтра Баттерворта номинал конденсатора в обратной связи (C2) должен быть вдвое больше, чем ёмкость C1. Поскольку номинал резисторов R5, R6 один и тот же, для плавной перестройки частоты среза подходит почти любой сдвоенный подстроечный резистор — именно поэтому во многих усилителях характеристики фильтров НЧ более стабильны, нежели характеристики фильтров ВЧ.
На рис. 8 показаны амплитудно-частотные характеристики фильтров второго порядка.
Рис. 8. Характеристики фильтров второго порядка
Вот теперь можно вернуться к тому вопросу, который остался без ответа. Схему фильтра первого порядка мы «проходили» потому, что активные фильтры создаются в основном путём каскадирования базовых звеньев. Так что последовательное соединение фильтров первого и второго порядка даст третий порядок, цепочка из двух фильтров второго порядка даст четвёртый и так далее. Поэтому я приведу лишь два варианта схем: фильтр ВЧ третьего порядка и фильтр НЧ — четвёртого. Тип характеристики — Баттерворт, частота среза — те же 100 Гц. (Рис. 9).
Рис. 9. Фильтр ВЧ третьего порядка
Предвижу вопрос: отчего вдруг изменились номиналы резисторов R3, R4, R5? А отчего бы им не измениться? Если в каждой «половинке» схемы уровню -3 дБ соответствовала частота 100 Гц, значит, совместное действие обеих частей схемы приведёт к тому, что спад на частоте 100 Гц составит уже 6 дБ. А мы так не договаривались. Так что самое привести методику выбора номиналов — пока только для фильтров Баттерворта.
1. По известной частоте среза фильтра задаться одним из характерных номиналов (R или C) и вычислить второй номинал, используя зависимость:
Fc = 1/(2πRC) (1.1)
Поскольку ассортимент номиналов конденсаторов, как правило, более узкий, разумнее всего задаться базовым значением ёмкости C (в фарадах), а по нему определить базовое значение R (Ом). Но если у вас, к примеру, есть пара конденсаторов 22 nF и несколько штук на 47 nF, никто не мешает вам брать и те, и эти — но в разных частях фильтра, если он составной.
2. Для фильтра первого порядка формула (1.1) даёт сразу значение резистора. (В нашем конкретном случае получаем 72,4 кОм, округляем до ближайшего стандартного значения, получаем 75 кОм.) Для базового фильтра второго порядка вы точно так же определяете стартовое значение R, но для того, чтобы получить действительные значения резисторов, надо будет воспользоваться таблицей. Тогда номинал резистора в цепи обратной связи определится как
Rp = KpR (1.2)
а номинал резистора, идущего в «землю», будет равен
Rs = KsR (1.3)
| Порядок фильтра | Kp | Ks |
| 2 | 0,7070 | 1,414 |
| 3 | 0,5000 | 2,000 |
| 4 (1) | 0,3827 | 2,613 |
| 4 (2) | 0,9240 | 1,082 |
Единичкой и двойкой в скобках обозначены строки, относящиеся к первому и второму каскадам фильтра четвёртого порядка. Можете проверить: произведение двух коэффициентов в одной строке равно единице — это, действительно, обратные величины. Впрочем, мы договорились в теорию фильтров не лезть.
Расчёт номиналов определяющих компонентов фильтра НЧ осуществляется сходным образом и по той же таблице. С той только разницей, что в общем случае вам придётся танцевать от удобного номинала резистора, а номиналы конденсаторов подбирать по таблице. Конденсатор в цепи обратной связи определится как
Cp = KsC, (1.4)
а конденсатор, соединяющий вход ОУ с «землёй», как
Cs = KpC (1.5)
Пользуясь вновь приобретёнными знаниями, рисуем фильтр НЧ четвёртого порядка, который уже вполне можно применить для работы с сабвуфером (рис. 10). На схеме я на этот раз привожу расчётные значения емкостей, без округления до стандартного номинала. Это чтобы вы могли себя проверить при желании.
Рис. 10. Фильтр НЧ четвёртого порядка
Я до сих пор ни слова не сказал о фазовых характеристиках, и правильно сделал — вопрос этот отдельный, отдельно им и займёмся. В следующий раз, вы же поняли, мы только начинаем…
Рис. 11. Характеристики фильтров третьего и четвёртого порядка
www.xn--80aeatqv1al.xn--p1ai
Поделиться с друзьями: