Выбор статьи по меткам03 (1)9 класс (3)10 класс (1)11 класс (2)12 (1)13 (С1) (3)14 февраля (1)15 задание ЕГЭ (2)16 задача профиль (1)18 (С5) (2)18 задача ЕГЭ (2)23 марта (1)2016 (2)C5 (1)А9 (1)Александрова (2)Архимед (1)Бернулли (1)Бойля-Мариотта (1)В8 (1)В12 (1)В13 (1)В15 (1)ВК (1)ВШЭ (1)ГИА физика задания 5 (1)Герона (1)Герцшпрунга-Рассела (1)Гринвич (1)ДВИ (1)ДПТ (1)Десятичные приставки (1)Дж (1)Диэлектрические проницаемости веществ (1)ЕГЭ 11 (2)ЕГЭ 14 (1)ЕГЭ 15 (2)ЕГЭ 18 (1)ЕГЭ С1 (1)ЕГЭ по математике (24)ЕГЭ по физике (18)ЕГЭ профиль (6)Европа (1)Задача 17 ЕГЭ (6)Задачи на движение (1)Закон Архимеда (2)Законы Ньютона (1)Земля (1)Ио (1)КПД (8)Каллисто (1)Кельвин (1)Кирхгоф (1)Койпера (1)Колебания (1)Коэффициенты поверхностного натяжения жидкостей (1)Ломоносов (2)Луна (1)МГУ (1)МКТ (7)Максвелл (2)Максвелла (1)Максимальное удаление тела от точки бросания (1)Менделеева-Клапейрона (1)Менелая (3)Метод наложения (2)Метод узловых потенциалов (1)Метод эквивалентных преобразований (1)НОД (1)ОГЭ (11)ОГЭ (ГИА) по математике (27)ОГЭ 3 (ГИА В1) (1)ОГЭ 21 (3)ОГЭ 21 (ГИА С1) (4)ОГЭ 22 (2)ОГЭ 25 (3)ОГЭ 26 (1)ОГЭ 26 (ГИА С6) (1)ОГЭ по физике 5 (1)ОДЗ (12)Обыкновенная дробь (1)Оорта (1)Основные физические константы (1)Отношение объемов (1)Показатели преломления (1)Показательные неравенства (1)Противо-эдс (1)Работа выхода электронов (1)Радиус кривизны траектории (1)Релятивистское замедление времени (1)Релятивистское изменение массы (1)С1 (1)С1 ЕГЭ (1)С2 (2)С3 (1)С4 (3)С6 (5)СУНЦ МГУ (2)Синхронная машина (1)Снеллиуса (2)Солнечной системы (1)Солнце (1)Средняя кинетическая энергия молекул (1)Таблица Менделеева (1)Текстовые задачи (8)ФИПИ (1)Фазовые переходы (1)Фаренгейт (1)Френеля (1)Цельсий (1)ЭДС (4)Электрохимические эквиваленты (1)абсолютная (1)абсолютная влажность (2)абсолютная звездная величина (1)абсолютная температура (1)абсолютный ноль (1)адиабаты (1)аксиомы (1)алгоритм Евклида (1)алгоритм Робертса (1)аморфное (1)амплитуда (3)аналитическое решение (1)анекдоты (1)апериодический переходной процесс (2)аргумент (1)арифметическая прогрессия (3)арифметической прогрессии (1)арки (1)арккосинус (1)арккотангенс (1)арксинус (1)арктангенс (1)архимеда (2)асинхронный (1)атмосферное (1)атомная масса (2)афелий (2)база (1)без калькулятора (1)белого карлика (1)бензин (1)бесконечная периодическая дробь (1)бесконечный предел (1)биквадратные уравнения (1)бипризма (1)биссектриса (2)биссектрисы (2)благоприятный исход (1)блеск (3)блок (1)боковой поверхности (1)большая полуось (1)бригада (2)бросили под углом (2)бросили со скоростью (2)броуновское движение (1)брошенного горизонтально (2)брусок (2)брусок распилили (1)быстрый способ извлечения (1)введение дополнительного угла (1)вектор (5)векторное произведение (2)велосипедисты (1)вероятность (1)вертикальная составляющая (1)вертикально вверх (1)вертикальные углы (1)вес (3)вес тела (1)ветви (1)ветвь (2)ветер (1)взаимодействие зарядов (1)видимая звездная величина (1)виртуальный банк (1)виртуальных перемещений (1)витка (1)виток (1)вклад (1)влажность (2)влажность воздуха (1)влетает (1)вневписанная окружность (2)внутреннее сопротивление (1)внутреннее сопротивление источника (1)внутреннюю энергию (1)внутренняя энергия (7)воды (1)возведение в квадрат (1)возвратные уравнения (2)воздушный шар (1)возрастающая (1)возрастет (1)волны (1)вписанная окружность (3)вписанной окружности (1)вписанный угол (4)в правильной пирамиде (1)вращение (1)времени (1)время (21)время в минутах (1)время выполнения (1)время движения (2)время падения (1)в стоячей воде (1)встретились (1)вступительный (1)вторая половина пути (1)вторичная (1)вторичная обмотка (1)вторичные изображения (1)второй закон Ньютона (3)выбор двигателя (1)выборка корней (4)выколотая точка (1)выразить вектор (1)высота (4)высота Солнца (1)высота столба (1)высота столба жидкости (1)высоте (3)высоту (1)высоты (3)выталкивающая сила (2)вычисления (1)газ (3)газа (1)галочка (1)гамма-лучей (1)гармоника (2)гвоздя (1)геометрическая вероятность (1)геометрическая прогрессия (3)геометрические высказывания (1)геометрический смысл (2)геометрическую прогрессию (1)геометрия (6)гигрометр (1)гидродинамика (1)гидростатика (3)гипербола (2)гипотенуза (3)гистерезисный двигатель (1)главный период (1)глубина (1)глухозаземленная нейтраль (1)гомотетия (2)горизонтальная сила (1)горизонтальную силу (1)гравитационная постоянная (1)градус (1)грани (1)график (1)графики функций (5)графически (1)графический способ (1)графическое решение (2)груз (2)группа (1)давление (23)давление жидкости (3)давление пара (1)дальность полета (1)двигатель с активным ротором (1)движение под углом (1)движение под углом к горизонту (3)движение по кругу (1)движение по течению (1)движение с постоянной скоростью (2)двойной фокус (1)двугранный угол при вершине (1)действительная часть (1)действующее значение (2)деление (1)деление многочленов (2)деление уголком (1)делимость (2)делимость чисел (1)делитель (1)демонстрационный варант (1)деталей в час (1)диаграмма (1)диаметр (2)динамика (4)диод (1)диск (1)дискриминант (4)дифракционная решетка (2)дифференцированный платеж (1)диффузия (1)диэлектрик (1)диэлектрическая проницаемость (1)длина (2)длина вектора (1)длина волны (7)длина отрезка (1)длина пружины (1)длина тени (1)длиной волны (2)длину нити (1)длительность разгона (1)длительный режим (1)добротность (1)догнал (1)догоняет (1)докажите (1)доля (1)дополнительный угол (1)досрочный (2)досрочный вариант (1)дптр (1)дуга (1)единицы продукции (1)единичный источник (1)единичных кубов (1)единственный корень (1)ежесекундно (1)емкость (7)емкость заряженного шара (1)естественная область определения (1)жесткость (4)жеткость (1)живая математика (2)жидкости (1)жидкость (1)завод (1)загадка (2)задание 13 (2)задание 15 (3)задание 23 (1)задания 1-14 ЕГЭ (1)задача 13 профиль (1)задача 14 профиль (3)задача 16 (1)задача 16 профиль (3)задача 18 (1)задача 26 ОГЭ (1)задача с параметром (6)задачи на доказательство (4)задачи на разрезание (4)задачи на совместную работу (3)задачи про часы (1)задерживающее напряжение (1)заземление (1)заказ (1)закон Гука (1)закон Ома (3)закон Снеллиуса (1)закона сохранения (1)закон движения (1)закон кулона (7)закон сложения классических скоростей (1)закон сохранения импульса (6)закон сохранения энергии (4)законы Кирхгофа (6)законы коммутации (1)закрытым концом (1)замена переменной (2)замкнутая система (2)зануление (1)запаянная (2)заряд (8)заряда (1)заряд конденсатора (1)защитная характеристика (1)звездочка (1)звезды (1)зенит (1)зенитное расстояние (1)зеркало (1)знак неравенства (1)знаменатель прогрессии (4)значение выражения (1)идеальный газ (5)извлечение в столбик (1)излом (1)излучение (2)изменение длины (2)изобара (1)изобаричесикй (1)изобарический (2)изобарный (1)изобарный процесс (1)изображение (2)изолированная нейтраль (1)изопроцессы (1)изотерма (2)изотермический (2)изотермический процесс (1)изотоп (1)изохора (1)изохорический (1)изохорный процесс (1)импульс (7)импульса (1)импульс силы (1)импульс системы (1)импульс системы тел (4)импульс тела (4)импульс частицы (1)индуктивно-связанные цепи (1)индуктивное сопротивление (1)индуктивность (1)индукцией (1)индукция (5)интеграл Дюамеля (1)интервал (1)интересное (3)интерференционных полос (1)иррациональность (2)испарение (2)исследование функции (4)источник (1)источник света (1)исход (1)камень (1)камешек (1)капилляр (1)карлик (1)касательная (4)касательные (1)касаются (1)катет (3)катушка (2)качаний (2)квадлратичная зависимость (1)квадрант (1)квадрат (3)квадратичная функция (3)квадратное уравнение (4)квадратную рамку (1)квант (1)квантов (1)кинематика (2)кинетическая (12)кинетическая энергия (4)кинетической (1)кинетической энергии (1)кинетическую энегрию (1)классический метод (3)классический метод расчета (1)ключ (1)кодификатор (1)колене (1)количество вещества (1)количество теплоты (8)коллектор (1)кольцо (1)комбинаторика (1)коммутация (1)комплексное сопротивление (1)комплексное число (1)комплексные числа (1)компонент (1)конвекция (3)конденсатор (10)конденсаторы (1)конечная температура (1)конечная температура смеси (1)конечный предел (1)консоль (1)контрольная (1)контрольные (1)контур (5)конус (3)концентрация (6)координата (5)координаты (3)координаты вектора (1)координаты середины отрезка (1)корабля (1)корень (2)корень квадратный (1)корень кубический (1)корни (2)корни иррациональные (1)корни квадратного уравнения (3)корни уравнения (1)корпоративных (1)косинус (2)косинусы (1)котангенс (1)коэффициент (1)коэффициент жесткости (1)коэффициент наклона (3)коэффициент поверхностного натяжения (3)коэффициент подобия (5)коэффициент трансформации (1)коэффициент трения (5)коэффициенты (1)красной границы (1)красный (1)кратковременный режим (1)кратные звезды (1)кредит (8)кредитная ставка (4)криволинейная трапеция (2)кристаллизация (1)критерии оценки (1)кружок (1)кулонова сила (1)кульминация (1)кусочная функция (1)левом колене (1)лед (1)лет (1)линейная скорость (2)линейное напряжение (1)линейное уравнение (2)линейный размер (1)линза (2)линии излома (1)линиями поля (1)линия отвеса (1)лифт (1)лифта (1)лифте (1)логарифм (7)логарифмические неравенства (3)логарифмические уравнения (1)логарифмическое неравенство (2)логарифмы (1)льда (1)магнитное поле (1)магнитном поле (1)магнитные цепи (1)максимальная высота (1)максимальная скорость (1)малых колебаний (1)масса (23)массе (1)массивная звезда (1)массовое содержание (1)массой (1)массу (1)математика (4)математический маятник (1)маятник (3)мгновенный центр вращения (1)медиана (1)меридиан (1)метод внутреннего проецирования (1)метод замены переменной (4)метод интервалов (3)метод комплексных амплитуд (3)метод контурных токов (1)метод координат (1)метод линий (1)методом внутреннего проецирования (1)метод переменных состояния (1)метод подстановки (4)метод рационализации (4)метод решетки (1)метод следов (5)метод сложения (4)метод телескопирования (1)метод узловых напряжений (1)методы расчета цепей (2)методы расчета цепей постоянного тока (1)метод эквивалентного генератора (2)механика (1)механическая характеристика (1)механическое напряжение (1)минимальная скорость (1)минимальной скоростью (1)минимум (1)мнимая единица (1)мнимая часть (1)многоугольник (1)многочлены (1)мода (2)модули (1)модуль (10)модуль Юнга (1)модуль средней скорости (1)молекулярно-кинетическая теория (2)моль (1)молярная масса (5)момент (5)момент инерции двигателя (1)момент нагрузки (1)момент сил (1)монотонная (1)монотонность функции (1)монохроматического (1)мощности силы тяжести (1)мощность (8)мощностью (1)мяч (1)наблюдатель (1)нагревание (1)нагреватель (1)нагревателя (1)нагрели (1)наибольшее (1)наивысшая точка (1)наименьшее (1)наименьшее общее кратное (1)наклон (1)наклонная плоскость (2)направление (1)направление обхода (3)направлении (1)направляющий вектор (1)напряжение (9)напряжение на зажимах (1)напряжение смещения нейтрали (2)напряженность (4)напряженность поля (6)насос (1)насоса (1)насыщенный пар (1)натяжение нити (5)натяжения (1)находился в полете (2)начальная температура (1)начальной скоростью (1)недовозбуждение (1)незамкнутая система (2)нелинейное сопротивление (1)неопределенность типа бесконечность на бесконечность (1)неопределенность типа ноль на ноль (1)непериодическая дробь (1)неравенства (8)неравенство (18)нерастяжимой нити (1)нерастянутой резинки (1)несимметричная нагрузка (1)несинусоидальный ток (3)нестандартные задачи (1)нестрогое (1)нечетная функция (2)нечетное (1)нечетность (1)неявнополюсный (1)нити (1)нити паутины (1)нить (1)новости (1)нормаль (1)нормальное ускорение (11)нулевой ток (2)обкладками (1)обкладках (1)обкладки (1)область допустимых значений (8)область значений (1)область определения (8)область определения функции (4)оборот (1)обратные тригонометрические функции (1)обратные функции (1)общая хорда (1)общее сопротивление (1)общее сопротивление цепи (1)объем (35)объемный расход (1)объемом (1)объем параллелепипеда (1)объем пирамиды (1)одинаковые части (1)окружность (12)окружность описанная (1)олимпиада (2)олимпиады по физике (2)они встретятся (1)операторный метод (4)оптика (1)оптическая разность хода (1)оптический центр (1)орбитам (1)орбитой (1)оригинал (1)осевое сечение (1)основание (2)основание логарифма (2)основания трапеции (1)основное тригонометрическое тождество (1)основное уравнение МКТ (2)основной газовый закон (1)основной период (1)основной уровень (1)основные углы (1)остаток (1)отбор корней (5)ответ (1)относительная (1)относительная влажность (3)относительно (2)относительность движениия (1)относительность движения (2)отношение (4)отношение времен (1)отношение длин (1)отношение площадей (3)отношение скоростей (2)отрезок (1)отсечение невидимых граней (1)очки (1)падает (1)падает луч (1)падает под углом (1)падение (2)падение напряжения (2)пар (2)парабола (5)параллакс (3)параллелепепед (2)параллелепипед (2)параллелограмм (4)параллелограмм Виньера (1)параллельно (1)параллельное соединение (3)параллельные прямые (1)параллельными граням (1)параметр (26)парообразование (1)парсек (1)парциальное (1)парциальное давление (1)паскаль (1)первичная (1)перевозбуждение (1)перегородка (1)перегрузок (1)переменное основание (2)перемещение (6)пересекает (1)пересечение (1)пересечения (1)переходная проводимость (1)переходное сопротивление (1)переходной процесс (1)переходные процессы (9)перигелий (2)периметр (2)период (12)периодическая дробь (1)период колебаний (1)период малых колебаний (1)период обращения (2)период функции (1)периоды (1)пион (1)пипетка (1)пирамида (7)пирамида шестиугольная (1)пирамиды (2)пирсона (1)плавание (1)плавкие предохранители (1)плавление (1)план (1)планете (1)планеты (3)планиметрия (9)планиметрия профиль (1)пластинами (1)пластинка (1)платеж (6)плечо (2)плоского зеркала (1)плоскопараллельная (1)плоскость (1)плоскость сечения (1)плотности веществ (1)плотность (21)плотность пара (3)плотность сосуда (1)плотность энергии (1)площади (2)площади фигур на клетчатой бумаге (1)площадь (21)площадь круга (1)площадь пластин (1)площадь поверхности (1)площадь под кривой (2)площадь проекции (1)площадь проекции сечения (1)площадь сектора (1)площадь сечения (5)площадь треугольника (1)поверхностная плотность заряда (1)поворот (1)повторно-кратковременный режим (1)погрешность (1)погружено (1)подготовка к контрольным (3)под каким углом (1)подмодульное (1)подмодульных выражений (1)подобен (1)подобие (6)подобия треугольников (1)подобны (1)подпереть (1)под углом (2)под углом к горизонту (1)показателем преломления (1)показатель преломления (4)поле (1)полезной работы (1)полезную мощность (1)полигон частот (1)по линиям сетки (1)полное ускорение (1)половина времени (1)половинный угол (1)полония (1)полость (1)полуокружность (1)полупроводник (1)по окружности (1)поправка часов (1)поршень (4)порядок решетки (2)последовательно (1)последовательное соединение (3)последовательность (1)посторонние корни (4)постоянная Авогадро (1)постоянная времени (1)постоянная скорость (1)постоянная составляющая (2)постоянный ток (5)построение (2)построение графика функции (1)потенциал (4)потенциал шара (1)потенциальная (13)потенциальная энергия (3)потенциальной (1)потери в стали (2)потеря корней (4)поток (4)по физике (1)правило левой (1)правило моментов (2)правильную пирамиду (1)правильный многоугольник (1)правом колене (1)предел функции (1)преломляющий угол (1)преобразование графиков функций (1)преобразования (1)преподаватели (2)пресс (2)призма (6)призмы (3)признаки подобия (4)признаки равенства треугольников (3)пробник (5)пробный вариант (2)провода (1)проводник (1)проводник с током (1)проводящего шара (1)проволоки (1)прогрессия (2)проекции ускорения (2)проекция (6)проекция перемещения (1)проекция скорости (4)проекция ускорения (2)производительность (2)производная (2)промежуток (1)промежуток знакопостоянства (1)пропорциональны (1)проскальзывает (1)проскальзывания (1)противоположное событие (1)противостояние (1)протона (1)прототипы (1)профиль (2)профильный ЕГЭ (1)процент (3)процентная ставка (6)процентное отношение (1)процентное содержание (2)проценты (1)пружин (1)пружина (2)пружинный маятник (1)прямая (6)прямое восхождение (2)прямой (1)прямоугольник (1)пузырек (1)пуля (1)путь (24)работа (14)работа газа (5)работа тока (1)работу выхода (2)рабочее тело (1)рабочие (1)равнобедренный (1)равновесие (3)равновесия (1)равновесное (1)равнодействующая (1)равноускоренное (3)равные (1)равные фигуры (1)радиальную ось (1)радикал (1)радиус (8)радиус колеса (1)радиус кривизны (1)радиус описанной сферы (1)радиус темного кольца в отраженном свете (1)разбор (1)разложение на множители (2)размах (1)разности температур (1)разность потенциалов (1)разность прогрессии (3)разность хода (1)разрежьте (1)разрезание (3)разрыв функции (1)рамка (2)рамка с током (1)раскрытие модуля (1)расписание (1)расположение корней квадратного трехчлена (1)распределение частот (1)рассеивающая (1)расстояние (17)расстояние между зарядами (1)расстояние на карте (1)расстояние от точки (1)раствор (2)растяжение (1)расходуется (1)расцепители (1)расчеты по формулам (1)рационализация (4)рациональные неравенства (1)реактивные элементы (1)реактивный двигатель (1)реакция опоры (2)реакция якоря (1)ребра (1)ребус (2)резервуар (1)резистор (1)рентгеновскую трубку (1)репетитор (1)решебник (1)решение тригонометрических уравнений (1)решение уравнений (2)решение уравнений больших степеней (1)розетка (1)ромб (1)ряд Фурье (1)сарай с покатой крышей (1)сближаются (1)сближения (1)сбрасывают с высоты (1)сверхгигант (2)светимость (2)свободно (1)свободного падения (1)свободно падает (1)свойства (2)свойства отрезков (1)свойства степени (1)свойства функции (1)свойства функций (1)свойства чисел (1)свойство биссектрисы (2)свойству биссектрисы (1)сдвинуть (1)сектор (1)секущая (2)серия решений (1)сертификация (6)сессия (1)сечение (13)сечение наклонной плоскостью (1)сидерический (1)сила (7)сила Архимеда (5)сила Лоренца (1)сила ампера (4)сила взаимодействия (4)сила на дно (1)сила натяжения (5)сила натяжения нити (4)сила поверхностного натяжения (3)сила реакции опоры (1)сила трения (3)сила тяготения (1)сила тяжести (3)сила упругости (1)силой (2)силу (1)силу натяжения (1)силы трения (2)символический метод (3)симметричная нагрузка (1)симметрия (2)синодический (1)синус (2)синусоида (1)синусоидальный закон (1)синусоидальный ток (5)синусы (1)синхронный компенсатор (1)система (2)система неравенств (7)система отсчета (1)система счисления (1)система уравнений (3)системы уравнений (3)скалярное произведение (3)склонение (1)скольжение (2)скоросмть (1)скоростей (1)скорости (2)скорости течения (1)скорость (34)скорость сближения (3)скорость света (1)скорость теплохода (1)скорость удаления (1)скорость частицы (1)скоростью (1)сложение векторов (1)сложная функция (1)смежные углы (1)смешанное число (1)смещение (1)снаряд (1)собирающая (2)событие (1)соединение звездой (1)соединение треугольником (1)сокращение (1)сокращение дробей (1)соленоид (1)солнечная система (1)сообщающиеся сосуды (2)соприкосновения (1)сопротивление (9)сопряженное (3)составляющая скорости (1)составляющие (1)составляющие скорости (3)сосудах (1)сосуде (1)сохранение энергии (1)спектра (2)спектральный класс (2)спецификация (1)спирт (1)сплава (1)сплавы (1)справочные данные (3)справочные материалы (12)сравнение чисел (2)среднее (1)среднее значение (1)среднюю линию (1)средняя квадратичная скорость (1)средняя скорость (5)срок (1)срок кредитования (1)стакан (1)статград (4)статика (1)стенка (1)степенная функция (1)степенные уравнения (1)степень (2)стереометрия (4)стержень (1)столб жидкости (2)столбик (3)столбик жидкости (2)столбчатая диаграмма (1)стрелки поравняются (1)строгое (1)студенты (2)сумма прогрессии (1)суммарный импульс (1)сумма ряда (1)сумма углов (2)суммирование (2)сумму (1)суперпозиция (1)сутки (1)сфера (4)сферы (2)таблица (1)таблица частот (1)тангенс (2)тангенциальное ускорение (1)твердое тело (1)телескопирование (1)тело (1)температура (20)температурный коэффициент сопротивления (1)тени (1)теорема Пифагора (3)теорема виета (5)теорема косинусов (3)теорема синусов (2)теореме косинусов (1)теоремы (1)теория вероятности (1)тепловое действие (1)тепловое равновесие (2)тепловой баланс (1)тепловой двигатель (1)теплоемкость (1)теплообмен (1)теплопередача (4)теплопроводность (2)теплота (1)теплота сгорания (1)теплоты (4)техника быстрого счета (1)ток (10)ток насыщения (1)топливо (1)точечный источник (1)точка касания (1)точка росы (1)точки перемены знака (1)траектории (1)траекторию (1)траектория (1)транзистор (1)трансформатор (1)трапеция (4)трение (1)тренировочная работа (1)тренировочные работы (1)трения (1)треугольная пирамида (1)треугольник (3)треугольник Паскаля (1)треугольника (1)треугольники (2)трехфазные цепи (2)тригонометрические выражения (2)тригонометрические уравнения (1)тригонометрия (9)троса (1)трубка (4)угловая скорость (2)угловая частота (2)угловой скоростью (2)углом (1)углы (1)угол между боковыми ребрами (1)угол между векторами (1)угол между плоскостями (2)угол между прямой и плоскостью (1)угол между прямыми (1)угол наклона (1)уголь (10)удельная (1)удельная теплоемкость (2)удельная теплота (1)удельная теплота парообразования (2)удельное сопротивление (1)удержать (1)удлинение (3)узел (2)умножение (1)умножение вектора на число (1)умножение на пальцах (1)упрощение (3)упрощение выражений (1)упругий удар (1)уравнение (4)уравнение Менделеева-Клапейрона (5)уравнение окружности (2)уравнение плоскости (1)уравнение теплового баланса (1)уравнению (1)уравнения (2)уравнения высоких степеней (1)уравнения высших степеней (1)урана (1)ускорение (22)ускорением (1)ускорение свободного падения (4)ускорений (1)ускоряющая разность потенциалов (1)условие плавания (1)условие равновесия (1)фазное напряжение (1)фигуры (1)физика (27)фиолетовый (1)фокальная плоскость (1)фокус (4)формула (1)формула Герона (1)формула Пика (1)формулы сокращенного умножения (2)фотон (4)фотонов (1)функции (1)функция (1)холодильник (1)холодильнику (1)хорда (3)целые числа (1)цель (1)центральный угол (4)центр вращения (1)центр масс системы (1)центробежная сила (1)центр тяжести (1)центр тяжести системы (1)цепи постоянного тока (13)цепь второго порядка (1)цепь первого порядка (4)цикл Карно (1)циклическая частота (2)цилиндр (1)часовой угол (1)части (4)частица (1)частных клиентов (1)частота (9)частота излучения (1)часть объема (1)человека (1)черная дыра (1)четная функция (3)четность (1)числовая пряма%D (1)число витков (1)шайбы (1)шар (1)шарик на нитке (1)шестерня (1)широта (1)широте (1)эволюция звезд (1)эквивалентная емкость (1)эквивалентная синусоида (1)экзамен (1)экспонента (2)экстремум (1)эксцентриситет (2)электрические цепи (8)электрического поля (1)электрон (3)электрона (1)электрон влетает (1)электростатика (2)электротехника (8)элонгация (1)энергия (8)энергия покоя (1)энергия поля (1)эскалатору (1)юмор (6)явнополюсный (1)ядерная физика (1)якорь (1)яма (1) easy-physic.ru Метод контурных токовпозволяет решать меньшее количество уравнений, чем при расчёте сложных электрических цепей методом уравнений Кирхгофа. Порядок расчёта: Выбираем произвольное направление контурного (расчётного) тока. Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от контурного (собственного) тока и контурных токов соседних контуров. Решаем полученную систему уравнений и рассчитываем контурные токи. Рассчитываем действительные токи ветвей по правилу: Если в ветви течёт один контурный ток, то действительный ток равен контурному току. Если два и более — то действительный равен их алгебраической сумме и направлен в сторону большего. Задача Найти и направить все токи в электрической цепи методом контурных токов. Используя алгоритм, составляется система уравнений: Пусть при решении получили контурные токи: Тогда можно рассчитать действительные токи: Рассмотрим метод узловых напряжений(двух узлов) на примере. Задача Определить токи ветвей и направить их. Порядок расчёта: обозначаем узлы А и Б: под узлом А обозначаем узел, к которому направлена большая ЭДС; все токи направляем к узлу А; рассчитываем проводимость каждой ветви по формуле : Рассчитываем напряжение между двумя узлами по формуле: В формулу Eвходит со знаком “+”, если она направлена к узлу А; если от узла — то со знаком “–”. Находим токи ветвей: Изменяем направление отрицательных токов. Методом эквивалентного генераторанаходят ток в одной ветви. Особенно удобно, если сопротивление этой ветви изменяется. Согласно теореме об эквивалентном генераторе, любой активный двухполюсник можно заменить эквивалентной ЭДС () и эквивалентным внутренним сопротивлением (). То, что обведено пунктиром на схеме 1, — активный двухполюсник: Схема 1А Схема 1Б Чтобы найти , надо разомкнуть ветвь АБ и найти напряжение на зажимах разомкнутой ветви. Оно будет равно: Чтобы найти , надо разомкнуть ветвь АБ, убрать все источники, оставив их внутренние сопротивления. Далее необходимо рассчитать сопротивление цепи по отношению к зажимам АБ. Это и будет. Если известны и, то: Задача Дано (для схемы 1А): Найти ток в цепи (методом эквивалентного генератора). Разомкнутая цепь приведена на схеме: Находим ток холостого хода: Найдём : Обходим контур по второму закону Кирхгофа так, чтобы он замкнулся через напряжение (лучше взять такой контур, где меньше элементов): Находим : Далее можно выразить искомый ток: Метод наложенияоснован напринципе наложения, согласно которому ток в каждой ветви может быть найден как алгебраическая сумма токов от действия каждой ЭДС в отдельности. Порядок расчёта: Поочерёдно оставляем в схеме по одному источнику, внутреннее сопротивление исключаемых источников также остаётся. Расставляем частичные токи (обозначаем их со штрихом). Находим действительный ток, как алгебраическую сумму частичных токов. Действительный ток направляем в сторону большего частичного. Например: Пусть , тогда. studfiles.net Тогда по закону Ома Но, с другой стороны, по закону Ома По первому закону Кирхгофа Но по закону Ома для участка с ЭДС Откуда выражаем расчетную ЭДС: Находим коэффициент пересчета: Находим реальные токи: Замечание: Так как исходные данные заданы с точностью до двух значащих цифр, окончательные результаты расчетов округляем также до двух значащих цифр, а в промежуточных расчетах оставляем три значащие цифры. Проверяем расчет при помощи баланса мощности. Мощность источников Мощность потребителей 8. МЕТОД КОНТУРНЫХ ТОКОВ При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют реальные токи ветвей. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить по второму закону Кирхгофа для независимых контуров. Следовательно, метод контурных токов более экономен, чем метод на основе законов Кирхгофа (в нем меньше уравнений). Вывод основных расчетных уравнений покажем на примере схемы с двумя независимыми контурами (Рис. 8.1). Рис. 8.1 Пусть в левом контуре по часовой стрелке течет контурный ток I11, а в правом (также по часовой стрелке) – контурный ток I22. Прежде всего, запишем соотношения между контурными и реальными токами. В схеме два контура. Они имеют одну общую ветвь (последовательно соединенные ЭДС E5 и сопротивление R5). Следовательно, в этой ветви течет как контурный ток первого контура (I11), так и контурный ток второго контура (I22). Но если контурный ток I11 течет сверху вниз, то контурный ток I22 течет снизу вверх. Алгебраическая сумма контурных токов будет равна реальному току ветви, то есть току I2. С учетом направления реального тока имеем: Очевидно, что в остальных ветвях с учетом направления реальных токов: Запишем уравнения по второму закону Кирхгофа для реальных токов: Подставим в (8.4) соотношения (8.1-8.3): Перегруппируем слагаемые в (8.5) и получим систему линейных алгебраических уравнений относительно контурных токов: Алгоритм расчета цепи методом контурных токов Пример 8.1: Найти неизвестные токи методом контурных токов (Рис. 8.2). Рис. 8.2 Выбираем независимые контуры по ячейкам схемы. Задаем направления контурных токов. В данном случае направим все контурные токи по часовой стрелке. Составляем уравнения по второму закону Кирхгофа для контурных токов. Для I контура. Собственное сопротивление контура состоит из R1, R6 и R5. По ветви с R6 текут два контурных тока I11 и I22 в противоположных направлениях. Значит, в уравнение по второму закону Кирхгофа для контура I ток I22 войдет с минусом: Для II контура. Собственное сопротивление контура состоит из R2, R7 и R6. По ветви с R6 ток I11 течет противоположно току I22. А ток I33 течет по ветви с R7 противоположно току I22. Значит, в уравнение по второму закону Кирхгофа для контура II токи I11 и I33 войдут с минусом: Для III контура. Собственное сопротивление контура состоит из R3, R4 и R7. По ветви с R7 течет ток I22 противоположно току I33. Значит, в уравнение по второму закону Кирхгофа для контура III ток I22 войдет с минусом: Объединяем уравнения (Пр. 8.1.1-Пр. 8.1.3) в систему, следя за тем, чтобы в уравнениях присутствовали все неизвестные токи и располагались они руг под другом. В уравнении (Пр. 8.1.1) нет тока I33. Значит, запишем его, умноженным на ноль. Аналогично поступим с током I11 в уравнении (Пр. 8.1.3): В числах система (Пр. 8.1.4) будет выглядеть так: Заметим, что система (Пр. 8.1.5) имеет главный определитель, симметричный относительно главной диагонали. Систему (Пр. 8.1.5) решим методом Крамера. Главный определитель системы: Контурные токи: Определяем реальные токи (См. Рис. 8.2): vunivere.ru 1.3 Метод контурных токов В методе контурных токов за основные неизвестные величины принимают контурные токи, которые замыкаются только по независимым контурам (главным контурам). Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы. Алгоритмом метода контурных токов: 1. Задаются направлением токов ветвей и обозначают их на схеме. 2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников тока независимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока. 3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока проходит только один контурный ток!). 4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов. 5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам. Задача 1.3.1. Определить токи в ветвях схемы рис. 1.3.1 методом контурных токов. Правильность решения проверить по балансу мощностей. Рис. 1.3.1 Решение 1. В соответствии с алгоритмом, зададимся направлением токов ветвей и обозначим их на схеме рис. 1.3.1. 2. Определяем независимые контура и выбираем направления контурных токов Iк1, Iк2, Iк3. 3. Поскольку в схеме имеется ветвь, содержащая источник тока J, контурный ток Iк3 = J, а для контурных токов Iк1 и Iк2 запишем систему уравнений метода контурных токов: {Iк1⋅ (R3+R6)−Iк2⋅R6−J⋅R3=−E1−E6Iк2⋅ (R4+R5+R6)−Iк1⋅R6−J⋅R4=E6 или { Iк1⋅ (R3+R6)−Iк2⋅R6 =−E1−E6+J⋅R3−Iк1⋅R6 +Iк2⋅ (R4+R5+R6)=E6+J⋅R4 Подставив значения сопротивлений, получаем численную систему уравнений метода контурных токов с двумя неизвестными контурными токами: { 25Iк1 −5Iк2=−5 −5Iк1+14Iк2=40 откуда Iк1=0,4 A; Iк2=3 A. 4. Определяем токи в ветвях схемы по методу контурных токов: I1=Iк1=0,4 A; I5=−Iк2=−3 A; I6=Iк2−Iк1=3−0,4=2,6 A. Хотя все токи в ветвях можно определить методом контурных токов (I3 = Iк3 – Iк1; I4 = Iк3 – Iк2), токи I3 и I4 определим по первому закону Кирхгофа. Составим уравнения по первому закону Кирхгофа: для узла a: −I5−J+I4=0, откуда I4=I5+J= (−3)+2=−1 A; для узла b: −I1−I3+J=0, откуда I3=J−I1=2−0,4=1,6 A. 5. Правильность решения проверяем по балансу мощностей. Предварительно находим напряжение на зажимах источника тока: Uad=φa−φd=J⋅R2+I3⋅R3+I4⋅R4−E2= =2⋅10+1,6⋅20+ (−1)⋅5−10=37 B. Тогда E2⋅J+Uad⋅J+E1⋅ (−I1)+E6⋅I6=J2⋅R2+I32⋅R3+I42⋅R4+I52⋅R5+I62⋅R6;10⋅2+37⋅2+15⋅ (−0,4)+30⋅2,6=22⋅10+1,62⋅20+ (−1)2⋅5+ (−3)2⋅4+2,62⋅5; 166 Вт=166 Вт. 16.10.2011, 124384 просмотра. rgr-toe.ru Метод контурных токов. Метод контурных токов используется для расчета как резистивных линейных цепей с постоянными токами, так и комплексных схем замещения линейных цепей с гармоническими токами. В расчет вводятся так называемые контурные или фиктивные токи, которые замыкаются в независимых замкнутых контурах. Независимые контуры отличаются друг от друга наличием хотя бы одной новой ветви. Контурные токи принимают за неизвестные, находят сначала их, и уже затем через контурные токи определяют неизвестные токи в ветвях. Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, число неизвестных можно существенно сократить, включая источники в разные контуры. В таких схемах применение этого метода наиболее рационально. Число неизвестных в данном методе равно количеству уравнений, которые необходимо составить по второму правилу Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока. Основой для расчёта режима работы любой электрической цепи являются законы Ома и правила Кирхгофа. С их помощью, зная параметры элементов электрической цепи можно определить протекающие в ней токи и действующие напряжения. Можно решить обратную задачу по определению параметров цепи, которые обеспечивают требуемые токи и напряжения. Расчет цепи методом контурных токов. Найти токи в ветвях схемы I1, I2, I3, I4 Дано: R1=5 Ом; R2=10 Ом; R3=10 Ом;R4=3 Ом; R5 =40 Ом; R6=7 Ом; E1 = 40 В; E2 = 10 В; J = 1 А = 1. Топология. Определяем общее число ветвей: p*=5. Определяем число ветвей с источниками тока: pит=1. Определяем число ветвей с неизвестными токами: p*- pит=4. Количество узлов q=3. Определяем необходимое и достаточное число контуров: M = p*-(q-1) = 5 – (3-1)= 3. Алгоритм расчета 2. Произвольно наносим на схему номера и направления 4-х неизвестных токов I1, I2 , I3, I4.. 3. Обозначаем на схеме контура I, II, III и произвольно выбираем направления их обхода и контурные токи в них I11, I22, I33. 4. Записываем выражения для токов в ветвях через контурные токи: I1=I11+I33, I2=I11- I22, I3= I22+ I33, I4= I22, I5= J 5. Составляем уравнения по второму правилу Кирхгофа для тех контуров, токи в которых неизвестны (для контуров без источника тока): I1R1 + I2R2 = E1, I3R1 – I2R2 +I4(R4+R6) = E2 6. В этой системе заменяем токи в ветвях выражениями, полученными в пункте 4: R3(I11 + I33) + R2(I11 – I22) = E1 R1(I22+I33) – R2(I11- I22) + I22(R4+R6) = E2 7. Подставим заданные числовые значения сопротивлений и ЭДС и после приведения подобных получим простую систему уравнений: 2I11 – I22 = 3А, 5I22 - 2I11= 1Аоткуда I11 = 2A, I22 = 1A 8. Подставим эти значения контурных токов в уравнений в п. 4 и окончательно получаем: I1 = 3A, I2 = 1A, I3 = 2A, I4 = 1A Основы электротехники и электроники: Курс лекций, страница 5. Расчет схемы методом контурных токов
Извините такой страницы Wp-content Uploads 2014 02 Dz-1 Metod-konturnyh-tokov Pdf не существует!
Вопрос 20. Расчёт сложных электрических цепей методом контурных токов.
Вопрос 21. Расчёт сложных электрических цепей методом двух узлов.
Вопрос 22. Расчёт сложных электрических цепей методом эквивалентного генератора.
Вопрос 23. Метод наложения.
Основы электротехники и электроники: Курс лекций, страница 5
 .
.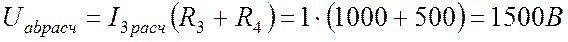 .
.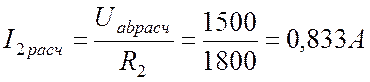 .
.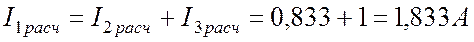 .
. .
.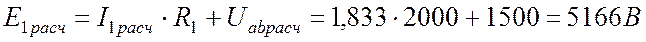 .
. .
.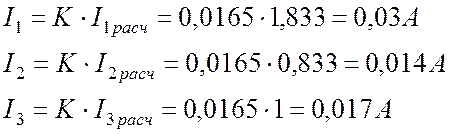 .
.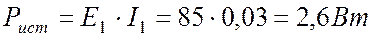 .
.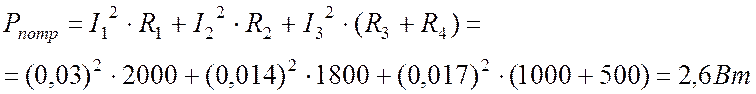 .
. .
.
 . (8.1)
. (8.1) , (8.2)
, (8.2)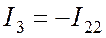 . (8.3)
. (8.3)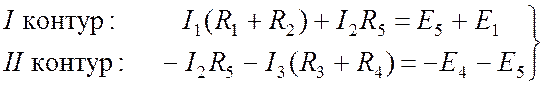 . (8.4)
. (8.4) . (8.5)
. (8.5)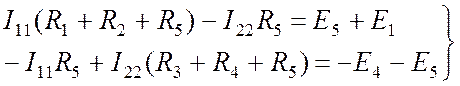 . (8.6)
. (8.6)
 . (Пр. 8.1.1)
. (Пр. 8.1.1)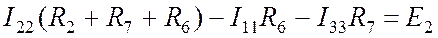 . (Пр. 8.1.2)
. (Пр. 8.1.2)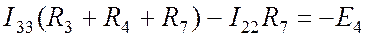 . (Пр. 8.1.3)
. (Пр. 8.1.3) . (Пр. 8.1.4)
. (Пр. 8.1.4) . (Пр. 8.1.5)
. (Пр. 8.1.5) .
. .
. .
. .
.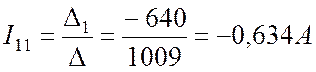 .
. .
.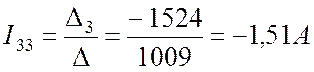 .
. .
.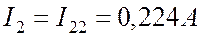 .
. .
. .
.
Метод контурных токов
Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях → 1.3 Метод контурных токов Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях 
 ветви связи, главные контуры, независимые контуры, метод контурных токов, контурные токи
ветви связи, главные контуры, независимые контуры, метод контурных токов, контурные токи Расчет цепи методом контурных токов.

Похожие статьи:
poznayka.org
1.8. Расчет цепей методом контурных токов.
Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.
Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.
При расчете рекомендуется придерживаться следующей последовательности:
– выделить все независимые контуры
– указать направления обхода контуров (желательно одно и то же для всех контуров)
– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)
– для всех независимых контуров составить уравнения второго закона Кирхгофа
– решить полученную систему уравнений любым известным методом
– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.
Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E1R3R1E1и R3E2R2R3. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R3, которая принадлежит двум контурам сразу, протекают два контурных тока IK1и IK2, но в противоположных направлениях.
E1 = IK1 (R1 + R3) – IK2R3
– E2= –IK1R3+IK2(R2+R3)
Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.
Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: IK1=7 A, IK2= – 5 A. Тогда I1= IK1= 7 = 7 A и протекает в резисторе R1так же, как контурный ток IK1по схеме сверху вниз. Ток I2= – IK2= – 5 А и протекает в резисторе R2по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R3 , цепи представленной на рис. 1.10, протекают контурный ток IK1= 7 А по схеме сверху вниз и контурный ток I2= – 5 А по схеме снизу вверх. IK1> IK2и I3= IK1– IK2= 7 – (–5) = 12 А. Ток I3имеет такое же направление, что и ток IK1 , т.е. по схеме сверху вниз.
1.9. Расчет цепей методом эквивалентного преобразования.
Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.
По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.
Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)
Например, в цепи представленной на рис. 1.11а приемники R3и R4соединены последовательно и их можно заменить одним эквивалентным с сопротивлением
R34= R3+ R4.
После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R2 и эквивалентный приемник R34включены параллельно. Параллельный участок R2– R34также можно заменить одним эквивалентным с сопротивлением
после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.
Входное сопротивление этой цепи R1234= R1+ R234
позволяет найти ток I1исходной цепи рис. 1.11а, пользуясь законом Ома
.
Напряжение на участке R234легко найти по закону Ома для пассивного участка цепи
U234= I1R234.
Токи в ветвях R2и R34также находятся по закону Ома
.
Токи I3= I4, т.к. приемники R3и R4включены последовательно, они равны току I34.
studfiles.net
Расчёт электрической цепи методом контурных токов
⇐ ПредыдущаяСтр 4 из 8Следующая ⇒Прежде, чем приступить к рассмотрению примера расчёта схемы методом контурных токов, рассмотрим основные положения этого метода и последовательность расчёта в соответствии с 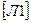 .
.
Сложные схемы характеризуются наличием значительного числа ветвей. В случае применения предыдущего метода это приводит к необходимости решать систему из значительного числа уравнений. Метод контурных токов позволяет уменьшить число исходных уравнений, а значит несколько облегчить расчёт.
При расчёте методом контурных токов используются понятия не зависимого контура и зависимого контура, которые использовались в предыдущем методе. Кроме них в этом методе используются ещё следующие понятия:
- собственный элемент контура - элемент, относящийся только к одному контуру;
- общий элемент контура - элемент, относящийся к двум и более контурам цепи.
Обозначаем, как и раньше, через К число узлов, а через n число ветвей цепи. Тогда число независимых контуров цепи определяется по уже известной формуле [n-(К-1)].
Метод основывается на предположении, что в каждом не зависимом контуре течёт собственный контурный ток, и вначале находят контурные токи в не зависимых контурах. Токи в ветвях цепи определяют через контурные токи. При этом исходят из того, что в собственных элементах контура токи совпадают с контурным током данного контура, а в общих элементах ток равен алгебраической сумме контурных токов тех контуров, к которым принадлежит данный элемент.
Последовательность расчёта:
1. Определяется число ветвей (n) и число узлов (К) цепи. Находится число независимых контуров [n-(К-1)].
2. Выбирается [n-(К-1)] не зависимых контура.
3. Выбирается условно-положительное направление контурных токов в каждом из независимых контуров (обычно показывается стрелкой).
4. Для каждого из независимых контуров составляется уравнение по второму закону Кирхгофа. При этом падение напряжения на собственных элементах определяется как произведение контурного тока на величину сопротивления, а на общих элементах - как произведение алгебраической суммы всех контурных токов, протекающих через данный элемент, на величину его сопротивле-
ния. Обход контура производится, как правило, в направлении собственного контурного тока.
5. Решается система из [n-(К-1)] уравнений и находятся контурные токи.
6. Токи в ветвях схемы находятся следующим образом:
- в собственных элементах контура ток равен контурному току;
- в общих элементах контура ток равен алгебраической сумме токов, протекающих через данный элемент.
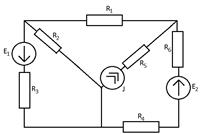
Пример применения метода контурных токов при расчёте электрических цепей рассмотрим на той же схеме (рис.6) и представим её на рис.11. Как рассматривалось выше, в этой схеме три независимых контура. Тогда в каждом независимом контуре выбираем направления контурных токов и показываем эти контурные токи.
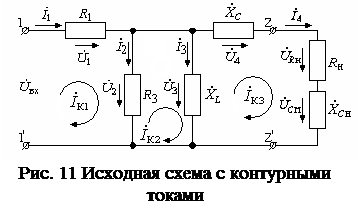 |
Для дальнейшего удобства расчёта расставим в схеме условно-положительные направления токов и напряжений. Далее, в соответствии с п.4 «последовательности расчёта», для каждого независимого контура составляем уравнения по второму закону Кирхгофа. В результате этих действий получаем систему (18) из трёх уравнений:
 (18)
(18)
В полученных уравнениях раскрываем скобки и приводим подобные:

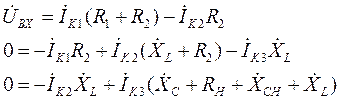 (19)
(19)
Из третьего уравнения системы (19) находим ток  :
:
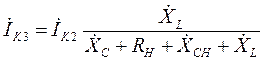 (20)
(20)
Подставляем выражение тока  (20) во второе уравнение системы (19), в результате чего, после приведения подобных членов, эта система принимает вид:
(20) во второе уравнение системы (19), в результате чего, после приведения подобных членов, эта система принимает вид:
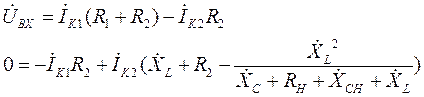 (21)
(21)
Во втором уравнении системы (21) коэффициент при токе 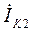 имеет довольно громоздкий вид. Для дальнейшего анализа будет удобно обозначить его какой-нибудь буквой, например
имеет довольно громоздкий вид. Для дальнейшего анализа будет удобно обозначить его какой-нибудь буквой, например 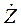 , т.к. этот коэффициент имеет размерность сопротивления:
, т.к. этот коэффициент имеет размерность сопротивления:
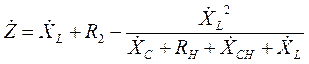 . (22)
. (22)
Подставим численные значения в формулу (22) и найдём значение 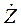 в алгебраической и показательной форме:
в алгебраической и показательной форме:
 (23)
(23)
С учётом (22) система уравнений (21) принимает вид:
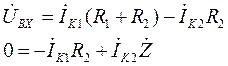 (24)
(24)
Из второго уравнения системы (24) найдём ток  :
:
 . (25)
. (25)
Подставим выражение для тока  (25) в первое уравнение системы (24) и после приведения к общему знаменателю, получим:
(25) в первое уравнение системы (24) и после приведения к общему знаменателю, получим:
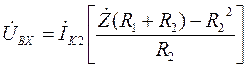 . (26)
. (26)
Из уравнения (26) находим ток 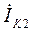 :
:
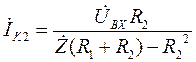 .
.
В полученное выражение для тока 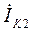 подставляем численные значения и находим значение тока в алгебраической и показательной форме:
подставляем численные значения и находим значение тока в алгебраической и показательной форме:
 .
.
Для определения тока  воспользуемся формулой (25), подставляем в неё численные значения и находим значение тока в алгебраической и показательной форме:
воспользуемся формулой (25), подставляем в неё численные значения и находим значение тока в алгебраической и показательной форме:
 .
.
Теперь определяем ток  , для чего используем формулу (20). Здесь удобнее будет использовать ток
, для чего используем формулу (20). Здесь удобнее будет использовать ток 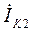 в показательной форме. Подставляем численные значения в (20) и в результате очевидных преобразований получим значение
в показательной форме. Подставляем численные значения в (20) и в результате очевидных преобразований получим значение  в показательной и алгебраической форме:
в показательной и алгебраической форме:
 .
.
После определения контурных токов переходим к определению токов в ветвях. В соответствии с методом расчёта токи в собственных ветвях контуров равны контурным токам этих контуров. В соответствии с этим находим токи  и
и  :
:
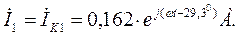


Токи в общих ветвях определяются как алгебраическая сумма контурных токов, протекающих через эти ветви. Ток 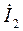 равен разности контурных токов
равен разности контурных токов  и
и 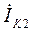 , так как они протекают через эту ветвь в противоположные стороны:
, так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов  и
и 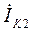 в алгебраической форме и находим значение тока
в алгебраической форме и находим значение тока 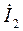 в алгебраической и показательной форме:
в алгебраической и показательной форме: 
Ток  равен разности контурных токов
равен разности контурных токов 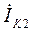 и
и  , так как они протекают через эту ветвь в противоположные стороны:
, так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов 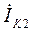 и
и  в алгебраической форме и находим значение тока
в алгебраической форме и находим значение тока  в алгебраической и показательной форме:
в алгебраической и показательной форме:
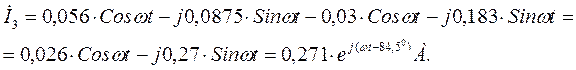

Находим напряжения на элементах:
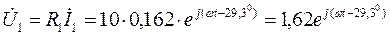 В.
В.
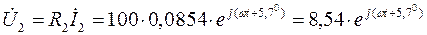 В.
В.
 В.
В.
 В.
В.
 В.
В.
Читайте также:
lektsia.com












Поделиться с друзьями: