1.3.9. Определите, какой заряд способны накопить конденсаторы, включенные по схеме, показанной на рисунке, если U = 350 В, а емкости всех конденсаторов равны между собой и составляют 0,5 мкФ. Определите, какую энергию способны накопить конденсаторы, включенные по схеме, приведенной на рисунке в задаче 1.3.9. Глава 2 Электрические цепи постоянного тока Сопротивление и проводимость проводников От чего зависит сопротивление проводника? Ответ: сопротивление зависит от площади сечения, материала и длины проводника. Заполните таблицу. 2.1.3. Определите сопротивление стальной проволоки длиной 200 м и площадью сечения 5 мм2. 2.1.4. Для радиоприемника необходимо намотать сопротивление 30 Ом из никелиновой проволоки площадью сечения 0, 21 мм2. Определите необходимую длину проволоки. Определите площадь сечения нихромовой проволоки длиной 20 м, если сопротивление ее равно 25 Ом. 2.1.6. Проволока площадью сечения 0,5 мм2 и длиной 40 м имеет сопротивление 16Ом. Определите материал, из которого она изготовлена. В каких единицах системы СИ измеряется электрическая проводимость? Ответ: Сименс (См) Определите проводимость проводников, если их сопротивления равны 5 Ом, 1кОм, 125 кОм, 1 МОм. 2.1.9. Медный стальной провода имеют одинаковые диаметр и длину. Какой из них сильнее нагревается при одной и той же силе тока? (Выберите правильный ответ) А) медный Б) стальной В) оба провода нагреются одинаково. Зависит ли сопротивление катушки, изготовленной из медного провода, от величины приложенного к ней напряжения? Ответ: нет независит. Во сколько раз увеличится сопротивление линии, если медный провод заменить стальным таких же длины и поперечного сечения? Ответ: сопротивление увеличится в 7-8 раз Как измениться проводимость проводника, если его длину и диаметр увеличили в два раза? Ответ: не изменится Как определить длину мотка медной проволоки, не разматывая его? Ответ: V=ST; T 2.1.14. Сверхпроводники – это материал, электрического сопротивления которого при понижении температуры до некоторой величины Тс понижается до ООМ. Как зависит от длины кабеля электрическое сопротивление его жилы и сопротивление изоляции? Ответ: Прямо пропорционально. Чем она длиннее, тем оно больше, 2.1.17. Обмотка трансформатора, изготовлена из медного провода, в нерабочем состоянии при температуре 150С имела сопротивление R1 =2 Ом. В ходе работы сопротивление ее стало R2 = 2,48 Ом. Определите температуру обмотки в рабочем состоянии, зная, что температурный коэффициент меди α = 0,004. Закон Ома Напишите формулы закона Ома для участка и полной цепи. I = Между какими величинами закон Ома для участка цепи устанавливает зависимость? Ответ: напряжение, сопротивление, сила тока. Заполните таблицу. Заполните таблицу. Как изменится ток в цепи, если напряжение увеличится в два раза? Ответ: увеличиться в 2 раза 2.2.6 Электрическая лампочка включена в сеть напряжением 220 В. Какой ток будет проходить через лампочку, если сопротивление ее нити 240 Ом? Читайте также: lektsia.com 1.3.9. Определите, какой заряд способны накопить конденсаторы, включенные по схеме, показанной на рисунке, если U = 350 В, а емкости всех конденсаторов равны между собой и составляют 0,5 мкФ. Определите, какую энергию способны накопить конденсаторы, включенные по схеме, приведенной на рисунке в задаче 1.3.9. Глава 2 Электрические цепи постоянного тока Сопротивление и проводимость проводников От чего зависит сопротивление проводника? Ответ: сопротивление зависит от площади сечения, материала и длины проводника. Заполните таблицу. 2.1.3. Определите сопротивление стальной проволоки длиной 200 м и площадью сечения 5 мм2. 2.1.4. Для радиоприемника необходимо намотать сопротивление 30 Ом из никелиновой проволоки площадью сечения 0, 21 мм2. Определите необходимую длину проволоки. Определите площадь сечения нихромовой проволоки длиной 20 м, если сопротивление ее равно 25 Ом. 2.1.6. Проволока площадью сечения 0,5 мм2 и длиной 40 м имеет сопротивление 16Ом. Определите материал, из которого она изготовлена. В каких единицах системы СИ измеряется электрическая проводимость? Ответ: Сименс (См) Определите проводимость проводников, если их сопротивления равны 5 Ом, 1кОм, 125 кОм, 1 МОм. 2.1.9. Медный стальной провода имеют одинаковые диаметр и длину. Какой из них сильнее нагревается при одной и той же силе тока? (Выберите правильный ответ) А) медный Б) стальной В) оба провода нагреются одинаково. Зависит ли сопротивление катушки, изготовленной из медного провода, от величины приложенного к ней напряжения? Ответ: нет независит. Во сколько раз увеличится сопротивление линии, если медный провод заменить стальным таких же длины и поперечного сечения? Ответ: сопротивление увеличится в 7-8 раз Как измениться проводимость проводника, если его длину и диаметр увеличили в два раза? Ответ: не изменится Как определить длину мотка медной проволоки, не разматывая его? Ответ: V=ST; T ; V= 2.1.14. Сверхпроводники – это материал, электрического сопротивления которого при понижении температуры до некоторой величины Тс понижается до ООМ. Как зависит от длины кабеля электрическое сопротивление его жилы и сопротивление изоляции? Ответ: Прямо пропорционально. Чем она длиннее, тем оно больше, 2.1.16. Провод состоит из одной стальной (ρ = 0,2410 Ом . м) и шести алюминиевых (ρ = 0,291 Ом . м) проволок диаметром 4,8 мм каждая. Определите сопротивление провода при температуре 20 0С. 2.1.17. Обмотка трансформатора, изготовлена из медного провода, в нерабочем состоянии при температуре 150С имела сопротивление R1 =2 Ом. В ходе работы сопротивление ее стало R2 = 2,48 Ом. Определите температуру обмотки в рабочем состоянии, зная, что температурный коэффициент меди α = 0,004. Закон Ома Напишите формулы закона Ома для участка и полной цепи. I = I = Между какими величинами закон Ома для участка цепи устанавливает зависимость? Ответ: напряжение, сопротивление, сила тока. Заполните таблицу. Заполните таблицу. Как изменится ток в цепи, если напряжение увеличится в два раза? Ответ: увеличиться в 2 раза 2.2.6 Электрическая лампочка включена в сеть напряжением 220 В. Какой ток будет проходить через лампочку, если сопротивление ее нити 240 Ом? Читайте также: lektsia.info Конденсатор - это устройство для накопления заряда и энергии электрического поля. Конструктивно это «бутерброд» из двух проводников и диэлектрика, которым может быть вакуум, газ, жидкость, органическое или неорганическое твердое тело. Первые отечественные конденсаторы (стеклянные банки с дробью, обклеенные фольгой) делали в 1752 г. М. Ломоносов и Г. Рихман. Что может быть интересного в конденсаторе? Приступая к работе над этой статьей я думал что смогу собрать и кратко изложить все об этой примитивной детальке. Но по мере знакомства с конденсатором, я с удивлением понимал, что здесь не рассказать и сотой доли всех сокрытых в нем тайн и чудес… Конденсатору уже более 250 лет, но он и не думает устаревать.. Кроме того, 1 кг «обычных просто конденсаторов» хранит меньше энергии чем килограмм аккумуляторов или топливных ячеек, но способен быстрее чем они выдать ее, развивая при этом большую мощность. - При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, импульсных лазерах с оптической накачкой и коллайдерах. Конденсаторы есть практически в любом приборе, поэтому если у вас нет новых конденсаторов, для опытов их можно выпаять оттуда. Заряд конденсатора - это абсолютное значение заряда одной из его обкладок. Он измеряется в кулонах и пропорционален числу лишних (-) или недостающих (+) электронов. Чтобы собрать заряд в 1 кулон, Вам понадобится 6241509647120420000 электрона. В пузырьке водорода, размером со спичечную головку их примерно столько же. Емкость конденсатора также равна q/U, где q – заряд положительной обкладки, U - напряжение между обкладками. Емкость зависит от геометрии конденсатора и диэлектрической проницаемости диэлектрика, и не зависит от заряда обкладок. В заряженном проводнике заряды стараются разбежаться друг от друга как можно дальше и потому находятся не в толще конденсатора, а в поверхностном слое металла, подобно пленке бензина на поверхности воды. Если два проводника образуют конденсатор, то эти избыточные заряды собираются друг напротив друга. Потому практически все электрическое поле конденсатора сосредоточено между его обкладками. На каждой обкладке заряды распределяются так, чтобы быть подальше от соседей. И расположены они довольно просторно: в воздушном конденсаторе с расстоянием между пластинами 1 мм, заряженном до 120 В, среднее расстояние между электронами составляет более 400 нанометров, что в тысячи раз больше расстояния между атомами (0,1-0,3 нм), а значит на миллионы поверхностных атомов приходится всего один лишний (или недостающий) электрон. Если уменьшить расстояние между обкладками, то силы притяжения возрастут, и при том же напряжении заряды на обкладках смогут «ужиться» плотнее. Увеличится емкость конденсатора. Так и сделал ничего не подозревавший профессор Лейденского университета ван Мушенброк. Он заменил толстостенную бутылку первого в мире конденсатора (созданного немецким священником фон Клейстом в 1745 г.) тонкой стеклянной банкой. Зарядил ее и потрогал, а очнувшись через два дня сообщил, что не согласится повторить опыт, даже если бы за это обещали французское королевство. Если поместить между обкладками диэлектрик, то они поляризуют его, то есть притянут к себе разноименные заряды из которых он состоит. При этом будет тот же эффект как если бы обкладки приблизились. Диэлектрик с высокой относительной диэлектрической проницаемостью можно рассматривать как хороший транспортер электрического поля. Но никакой транспортер не идеален, поэтому какой бы мы чудесный диэлектрик не добавили поверх уже имеющегося, емкость конденсатора только снизится. Повысить емкость можно только если добавлять диэлектрик (а еще лучше - проводник) вместо уже имеющегося но обладающего меньшей ε. В диэлектриках свободных зарядов почти нет. Все они зафиксированы то ли в кристаллической решетке, или в молекулах – полярных (представляющих собой диполи) или нет. Если внешнего поля нет, диэлектрик неполяризован, диполи и свободные заряды разбросаны хаотически и диэлектрик собственного поля не имеет. в электрическом поле он поляризуется: диполи ориентируются по полю. Так как молекулярных диполей очень много, то при их ориентации, плюсы и минусы соседних диполей внутри диэлектрика компенсируют друг друга. Нескомпенсированными остаются только поверхностные заряды – на одной поверхности – одного, на другой - другого. Свободные заряды во внешнем поле также дрейфуют и разделяются. При этом разные процессы поляризации идут с разной скоростью. Одно дело – смещение электронных оболочек, происходящее практически мгновенно, другое дело – поворот молекул, особенно больших, третье – миграция свободных зарядов. Последние два процесса, очевидно, зависят от темературы, и в жидкостях идут гораздо шустрее, чем в твердых телах. Если нагреть диэлектрик, повороты диполей и миграция зарядов ускорится. Если поле выключить, деполяризация диэлектрика происходит тоже не мгновенно. Он остается некоторое время поляризованным, пока тепловое движение не разбросает молекулы в исходное хаотическое состояние. Поэтому, для конденсаторов, где переключается полярность с высокой частотой пригодны только неполярные диэлектрики: фторопласт, полипропилен. Если разобрать заряженный конденсатор, а потом собрать (пластмассовым пинцетом), энергия никуда не денется, и светодиод сможет моргнуть. Он даже моргнет если подключить его к конденсатору в разобранном состоянии. Оно и понятно – при разборке заряд с пластин никуда не делся, а напряжение даже выросло, поскольку уменьшилась емкость и теперь обкладки прямо-таки распирает от зарядов. Стоп, как это напряжение выросло, ведь тогда вырастет и энергия? Так и есть, мы же сообщили системе механическую энергию, преодолевая кулоновское притяжение обкладок. Собственно, в этом и фишка электризации трением – зацепить электроны на расстоянии порядка размеров атомов и оттащить на макроскопическое расстояние, тем самым повысив напряжение с нескольких вольт (а таково напряжение в химических связях) до десятков и сотен тысяч вольт. Теперь понятно, почему синтетическая кофта бьется током не когда ее носишь, а только когда ее снимаешь? Стоп, а почему не до миллиардов? Дециметр же в миллиард раз больше ангстрема, на котором мы урвали электроны? Да потому что работа по перемещению заряда в электрическом поле равна интегралу Eq по d и это самое E ослабевает с расстояние квадратично. А если бы на всем дециметре между кофтой и носом было такое же поле как внутри молекул, то щелкнул бы по носу и миллиард вольт. Проверим это явление – повышение напряжения при растягивании конденсатора – экспериментально. Я написал простую программку на Visual Basic для приема данных с нашего контроллера ПМК018 и вывода их на экран. В общем, берем две 200х150 мм пластины текстолита, покрытого с одной стороны фольгой и припаиваем проводки, идущие к измерительному модулю. Затем кладем на одну из них диэлектрик – лист бумаги – и накрываем второй пластиной. Пластины прилегают неплотно, поэтому придавим их сверху корпусом авторучки (если давить рукой, то можно создать помехи). Схема измерения простая: потенциометр R1 устанавливает напряжение (в нашем случае это 3 вольта), подаваемое на конденсатор, а кнопка S1 служит для того чтобы подавать его на конденсатор, или не подавать. Итак, нажмем и отпустим кнопку – мы увидим график, показанный слева. Конденсатор быстро разряжается через вход осциллографа. Теперь попробуем во время разряда ослабить давление на пластины – увидим пик напряжения на графике (справа). Это как раз искомый эффект. При этом расстояние между обкладками конденсатора растет, емкость падает и потому конденсатор начинает разряжаться еще быстрее. Тут я не на шутку задумался.. Кажется, мы на пороге великого изобретения…Ведь если при раздвигании обкладок на них растет напряжение, а заряд остается прежним, то можно ведь взять два конденсатора, на одном раздвигать на них обкладки, а в точке максимального раздвижения передать заряд неподвижному конденсатору. Потом вернуть обкладки на место и повторить то же самое наоборот, раздвигая другой конденсатор. По идее напряжение на обоих конденсаторах будет расти с каждым циклом в определенное число раз. Отличная идея для электрогенератора! Можно будет создать новые конструкции ветряков, турбин и всего такого! Так, прекрасно… для удобства можно разместить все это на двух дисках, вращающихся в противоположные стороны…. ой что же это… тьфу, это же школьная электрофорная машина! :( В качестве генератора она не прижилась, так как неудобно иметь дело с такими напряжениями. Но на наноуровне все может измениться. Магнитные явления в наноструктурах во много раз слабее электрических, а электрические поля там, как мы уже убедились, огромны, поэтому молекулярная электрофорная машина может стать весьма популярной. Конденсатор как хранитель энергии Убедиться, что в самом ничтожнейшем конденсаторе хранится энергия очень легко. Для этого нам понадобится прозрачный светодиод красного свечения и источник постоянного тока (батарейка 9 вольт подойдет, но если номинальное напряжение конденсатора позволяет, лучше взять побольше). Опыт заключается в том чтобы зарядить конденсатор, а потом подключить к нему светодиод (не забываем про полярность), и смотреть как он моргнет. В темной комнате видна вспышка даже от конденсаторов в десятки пикофарад. Это каких-нибудь сто миллионов электронов испускают сто миллионов фотонов. Впрочем это не предел, ведь человеческий глаз может замечать куда более слабый свет. Просто я не нашел еще менее ёмких конденсаторов. Если же счет пошел на тысячи микрофарад, пожалейте светодиод, а вместо этого замыкайте конденсатор на металлический предмет чтобы увидеть искру – очевидное свидетельство наличия в конденсаторе энергии. Энергия заряженного конденсатора ведет себя во многом подобно потенциальной механической энергии - энергии сжатой пружины, поднятого на высоту груза или водонапорного бачка (а энергия катушки индуктивности, наоборот, подобна кинетической). Способность конденсатора накапливать энергию издавна применяется для обеспечения непрерывной работы устройств при кратковременных спадах питающего напряжения – от часов до трамваев. Конденсатор также используется для накопления «почти вечной» энергии, вырабатываемой тряской, вибрацией, звуком, детектированием радиоволн или излучения электросетей. Мало-помалу накопленная энергия от таких слабых источников в течение долгого времени позволяет затем некоторое время работать беспроводным датчикам и другим электронным приборам. На этом принципе основана вечная «пальчиковая» батарейка для устройств со скромным энергопотреблением (вроде ТВ пультов). В ее корпусе находится конденсатор емкостью 500 миллифарад и генератор, подпитывающий его при колебаниях с частотой 4–8 герц дармовой мощностью от 10 до 180 милливатт. Разрабатываются генераторы на основе пьезоэлектрических нанопроводков, способные направлять в конденсатор энергию таких слабых вибраций, как биения сердца, удары подошв обуви по земле, и вибрации технического оборудования. Еще один источник дармовой энергии – торможение. Обычно при торможении транспорта энергия переходит в тепло, а ведь ее можно сохранить и затем использовать при разгоне. Особенно остро стоит эта проблема для общественного транспорта, который тормозит и разгоняется у каждой остановки, что ведет к значительному расходу топлива и загрязнению атмосферы выхлопами. В Саратовской области в 2010 г. фирмой «Элтон» создан «Экобус» - экспериментальная маршрутка с необычными электродвигателями «мотор-колесо» и суперконденсаторами – накопителями энергии торможения, снижающими энергопотребление на 40%. Там применены материалы, разработанные в проекте «Энергия-Буран», в частности, углеродная фольга. Вообще, благодаря созданной еще в СССР научной школе, Россия является одним из мировых лидеров в сфере разработки и производства электрохимических конденсаторов. Например, продукция «Элтона» экспортируется за рубеж с 1998 года, а недавно в США началось производство этих изделий по лицензии российской компании. Емкость одного современного конденсатора (2 фарады, фото слева) в тысячи раз превышает емкость всего земного шара. Они способны хранить электрический заряд в 40 Кулон! Используются они, как правило, в автомобильных аудиосистемах, чтобы снизить пиковую нагрузку на электропроводку автомобиля (в моменты мощных бас-ударов) и за счёт огромной ёмкости конденсатора подавить все высокочастотные помехи в бортовой сети. А вот этот советский «дедушкин сундучок» для электронов (фото справа) не столь емок, но зато выдерживает напряжение в 40.000 вольт (обратите внимание на фарфоровые чашечки, защищающие все эти вольты от пробоя на корпус конденсатора). Это очень удобно для «электромагнитной бомбы», в которой конденсатор разряжается на медную трубочку, которая в тот же момент сжимается снаружи взрывом. Получается очень мощный электромагнитный импульс, выводящий из строя радиоаппаратуру. Кстати, при ядерном взрыве, в отличие от обычного, тоже выделяется электромагнитный импульс, что еще раз подчеркивает сходство уранового ядра с конденсатором. Кстати, такой конденсатор вполне можно напрямую зарядить статическим электричеством от расчески, только конечно заряжать до полного напряжения придется долго. Зато можно будет повторить печальный опыт ван Мушенброка в очень усугубленном варианте. Если просто потереть об волосы авторучку (расческу, воздушный шарик, синтетическое белье и т.п.), то светодиод от нее гореть не будет. Это потому, что избыточные (отнятые у волос) электроны заневолены каждый в своей точке на поверхности пластика. Поэтому если даже мы и попадем выводом светодиода в какой-то электрон, другие не смогут устремиться за ним и создать нужный для заметного невооруженным глазом свечения светодиода ток. Другое дело, если перенести заряды с авторучки в конденсатор. Для этого возьмем конденсатор за один вывод и буде тереть авторучку по очереди то о волосы, то о свободный вывод конденсатора. Почему именно тереть? Чтобы по максимуму собрать урожай электронов со всей поверхности ручки! Несколько раз повторим этот цикл и подключим к конденсатору светодиод. Он моргнет, причем только при соблюдении полярности. Так конденсатор стал мостиком между мирами «статического» и «обычного» электричества :) Я взял для этого опыта высоковольтный конденсатор, опасаясь пробоя низковольтного, но оказалось, что это излишняя предосторожность. При ограниченной подаче заряда напряжение на конденсаторе может быть намного меньше напряжения источника питания. Конденсатор может преобразовывать большое напряжение в малое. Например, статическое высоковольтное электричество – в обычное. В самом деле, есть ли разница: зарядить конденсатор одним микрокулоном от источнка напряжением 1 В или 1000 В? Если этот конденсатор настолько емкий, что от заряда в 1 мкКл на нем напряжение не повысится выше напряжения одновольтового источника питания (т.е. емкость его выше 1 мкф), то разницы нет. Просто если не ограничивать принудительно кулоны, то от высоковольного источника их захочет прибежать больше. Да и тепловая мощность, выделившаяся на выводах конденсатора будет больше (а количество теплоты то же, просто оно быстрее выделится, оттого и мощность больше). В общем, видимо, для этого опыта годится любой конденсатор емкостью не более 100 нф. Можно и более, но понадобится долго его заряжать чтобы получить достаточное для светодиода напряжение. Зато, если токи утечки в конденсаторе невелики, светодиод будет гореть дольше. Можно подумать о создании на этом принципе устройства подзарядки сотового телефона от трения его об волосы во время разговора :) Отличным высоковольтным конденсатором является отвертка. При этом ручка ее служит диэлектриком, а металлический стержень и рука человека – обкладками. Мы знаем, что натертая об волосы авторучка притягивает клочки бумаги. Если натирать об волосы отвертку то ничего не выйдет – металл не обладает способностью отнимать электроны у белков – она как не притягивала бумажки, так и не стала. Но если как в предыдущем опыте тереть ее заряженной авторучкой – отвертка, вследствие своей малой емкости, быстро заряжается до высокого напряжения и бумажки начинают к ней притягиваться. Впрочем, к чему такие сложности - есть же видеосъемка. На ней видно, что вспыхивает светодиод довольно ярко: Когда конденсаторы заряжают до высоких напряжений, начинает играть свою роль краевой эффект, состоящий в следующем. Если диэлектрик на воздухе поместить между обкладками и приложить к ним постепенно повышающееся напряжение, то при некотором значении напряжения на краю обкладки возникает тихий разряд, обнаруживаемый по характерному шуму и свечению в темноте. Величина критического напряжения зависит от толщины обкладки, остроты края, рода и толщины диэлектрика и пр. Чем диэлектрик толще, тем выше кр. Например, чем диэлектрическая постоянная диэлектрика выше, тем оно ниже. Для уменьшения краевого эффекта края обкладки заделывают в диэлектрик с высокой электрической прочностью, утолщают диэлектрик прокладку на краях, закругляют края обкладок, создают на краю обкладок зону с постепенно падающим напряжением за счет изготовления краев обкладок из материала с высоким сопротивлением, уменьшением напряжения, приходящегося на один конденсатор путем разбивки его на несколько последовательно включенных. Вот почему отцы-основатели электростатики любили чтобы на конце электродов были шарики. Это, оказывается, не дизайнерская фишка, а способ максимально уменьшить стекание заряда в воздух. Дальше уже некуда. Если кривизну какого-то участка на поверхности шарика еще уменьшить,то неизбежно возрастет кривизна соседних участков. Да и тут по-видимому в наших электростатических делах важна не средняя а максимальная кривизна поверхности, которая минимальна, конечно у шарика. Хм.. но если емкость тела это способность накапливать заряд, то она, наверное, весьма различна для положительных и отрицательных зарядов…. Представим себе сферический конденсатор в вакууме… От души зарядим его отрицательно, не жалея электростанций и гигаватт-часов (вот чем хорош мысленный эксперимент!)… но в какой-то момент избыточных электронов станет на этом шаре так много, что они попросту начнут разлетаться по всему вакууму, лишь бы не находиться в такой электроотрицательной тесноте. А вот с положительным зарядом такого не произойдет – электроны, как бы их мало не осталось, никуда из кристаллической решетки конденсатора не улетят. Что же получается, положительная емкость заведомо намного больше отрицательной? Нет! Потому что электроны там вообще-то были не для нашего баловства, а для соединения атомов, и без сколь-нибудь заметной их доли, кулоновское отталкивание положительных ионов кристаллической решетки мгновенно разнесет в пыль самый бронированный конденсатор :) На самом же деле, без вторичной обкладки, емкость «уединенных половинок» конденсатора очень мала: электроемкость уединенного куска провода диаметром 2 мм и длиной 1 м равна приблизительно 10 пФ, а всего земного шара – 700 мкф. Можно построить абсолютный эталон емкости, рассчитав его емкость по физическим формулам исходя из точных измерений размеров обкладок. Так и сделаны самые точные конденсаторы в нашей стране, которые находятся в двух местах. Государственный эталон ГЭТ 107-77 находится в ФГУП СНИИМ и состоит из 4-х безопорных коаксиально-цилиндрических конденсаторов, емкость которых рассчитывается с высокой точностью через скорость света и единицы длины и частоты, а также высокочастотного емкостного компаратора, позволяющего сравнивать емкости приносимых на поверку конденсаторов с эталоном (10 пф) с погрешностью менее 0,01% в диапазоне частот 1-100 МГц (фото слева). Эталон ГЭТ 25-79 (фото справа), находящийся в ФГУП ВНИИМ им. Д.И. Менделеева содержит расчетный конденсатор и интерферометр в вакуумном блоке, емкостный трансформаторный мост в комплекте с мерами емкости и термостатом и источники излучения со стабилизированной длиной волны. В основу эталона положен метод определения приращений емкости системы перекрестных электродов расчетного конденсатора при изменении длины электродов на заданное количество длин волн высокостабильного светового излучения. Это обеспечивает поддержание точного значения емкости 0,2 пф с точностью выше 0,00005 % Но на радиорынке в Митино я затруднился найти конденсатор с точностью выше 5% :( Что ж, попробуем рассчитать емкость по формулам на основе измерений напряжения и времени через наш любимый ПМК018. Будем рассчитывать емкость двумя способами. Первый способ основан на свойствах экспоненты и отношении напряжений на конденсаторе, измеренных в разные моменты разряда. Второй - на измерении заряда, отданного конденсатором при разряде, он получается интегрированием тока по времени. Площадь, ограниченная графиком тока и осями координат, численно равна заряду, отданному конденсатором. Для этих расчетов нужно точно знать сопротивление цепи через которую разряжается конденсатор. Это сопротивление я задал прецизионным резистором на 10 кОм из электронного конструктора. И вот результаты эксперимента. Обратите внимание на то какая красивая и гладкая получилась экспонента. Она ведь не математически рассчитана компьютером, а непосредственно измерена из самой природы. Благодаря координатной сетке на экране видно, что точно соблюдается свойство экспоненты - через равные промежутки времени уменьшаться в равное количество раз (я даже линейкой мерил на экране :) Таким образом, мы видим, что физические формулы вполне адекватно отражают окружающую нас реальность. Как видим, измеренная и рассчитанная емкость приблизительно совпадает с номинальной (и с показаниями китайских мультиметров), но не точь-в-точь. Жаль, что нет эталона, чтобы определить какая из них все-таки истинна! Если кто-нибудь знает эталон емкости, недорогой или доступный в быту – обязательно напишите об этом здесь, в комментариях. В силовой электротехнике первым в мире применил конденсатор Павел Николаевич Яблочков в 1877 г. Он упростил и вместе с тем усовершенствовал конденсаторы Ломоносова, заменив дробь и фольгу жидкостью, и соединив банки параллельно. Ему принадлежит не только изобретение инновационных дуговых ламп, покоривших Европу, но и ряд патентов, связанных с конденсаторами. Попробуем собрать конденсатор Яблочкова, используя подсоленную воду в качестве проводящей жидкости, а в качестве банки – стеклянную банку из по овощей. Получилась емкость 0,442 нф. Заменим банку полиэтиленовым пакетом, имеющим большую площадь и во много раз меньшую толщину – емкость вырастет до 85,7 нф. (Сначала наполним пакет водой и проверим, нет ли токов утечки!) Конденсатор работает – даже позволяет моргнуть светодиодом! Он также успешно выполняет свои функции в электронных схемах (я попробовал его включить в генератор вместо обычного конденсатора - все работает). Вода тут играет весьма скромную роль проводника, и если есть фольга, то можно обойтись без нее. Так сделаем, вслед за Яблочковым, и мы. Вот конденсатор из слюды и медной фольги, емкостью 130 пф. Металлические обкладки должны возможно плотно прилегать к диэлектрику, причем надо избегать введения между обкладкой и диэлектриком клеящего вещества, которое вызовет добавочные потери на переменном токе. Поэтому теперь в качестве обкладок применяют главным образом металл, химически или механически осажденный на диэлектрик (стекло) или плотно припрессованный к нему (слюда). Вы можете сами провести такие опыты с веществами, имеющими разную диэлектрическую проницаемость. Как вы думаете, что имеет большую диэлектрическую проницаемость, дистиллированная вода или масло? Соль или сахар? Парафин или мыло? Почему? Диэлектрическая проницаемость зависит много от чего... про нее можно было бы написать целую книгу. mntc.livejournal.com История создания. В 1745 году был создан первый конденсатор — «лейденская банка». Она представляла собой закупоренную наполненную водой стеклянную банку, оклеенную внутри и снаружи фольгой. Сквозь крышку в банку был воткнут металлический стержень. Лейденская банка позволяла накапливать и хранить сравнительно большие заряды, порядка микрокулона. Изобретение лейденской банки стимулировало изучение электричества, в частности скорости его распространения и электропроводящих свойств некоторых материалов. Выяснилось, что металлы и вода - лучшие проводники электричества. Благодаря Лейденской банке удалось впервые искусственным путем получить электрическую искру. Однако при раскопках был найден глиняный сосуд неизвестного назначения, внутри которого стоял медный пустотелый цилиндр с железным стержнем, укрепленным по центру асфальтовой пробкой. Вскоре американский химический журнал опубликовал гипотезу о назначении загадочного сосуда. Авторы гипотезы, указывая, что на дне сосуда найдены остатки оливкового масла, считают, что он служил конденсатором, причем цилиндр и стержень были обкладками, а масло, налитое в сосуд,— диэлектриком. Конденсатор заряжали, многократно перенося заряд на стержень с какого-либо диэлектрика, натертого о шерсть или мех. Затем можно было получить от банки сильный разряд. Не здесь ли, пишет журнал, следует искать исток легенды о волшебной лампе Аладина? Помните, чтобы вызвать джинна, следовало применить странный способ — как следует потереть лампу. В сказках разных народов мира встречается множество волшебных предметов, но ни один из них не требует такого обращения. Все становится понятным, если считать, что джинн — это поражавший воображение зрителей электрический разряд и что в сказке с некоторыми поэтическими вольностями описан способ зарядки лейденской банки. На вопрос, для чего могли служить такие конденсаторы, можно ответить: для зажигания священного огня в храме, для эффектной демонстрации перед верующими непонятной и невидимой силы, заключенной в волшебном сосуде. Не исключено и применение электрического разряда в более полезных целях. Еще древние римляне лечили радикулит »и некоторые другие заболевания, сажая больного на электрического ската. Но, насколько известно, никаких опытов, подтверждающих работоспособность такого конденсатора, проведено не было. На принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1000000 пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, т.е. постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 – 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, т.е. на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду. Основной характеристикой конденсатора является его ёмкость. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад. Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения. Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов. Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя. Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается. Многие конденсаторы с оксидным диэлектриком функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса. Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения. Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе. При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков. По виду диэлектрика различают такие типы конденсаторов:- Конденсаторы вакуумные - обкладки без диэлектрика находятся в вакууме.- Конденсаторы с газообразным диэлектриком.- Конденсаторы с жидким диэлектриком.- Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные, слюдяные, керамические, тонкослойные из неорганических плёнок.- Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные, комбинированные — бумажноплёночные, тонкослойные из органических синтетических плёнок.- Электролитические и оксидно-полупроводниковые конденсаторы. Такие конденсаторы отличаются от всех прочих типов прежде всего своей огромной удельной ёмкостью. В качестве диэлектрика используется оксидный слой на металлическом аноде. Вторая обкладка (катод) — это или электролит (в электролитических конденсаторах) или слой полупроводника (в оксидно-полупроводниковых), нанесённый непосредственно на оксидный слой. Анод изготовляется, в зависимости от типа конденсатора, из алюминиевой, ниобиевой или танталовой фольги. В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляюшие, дозиметрические, пусковые и другие конденсаторы. Форум по конденсаторам Обсудить статью КОНДЕНСАТОРЫ radioskot.ru Наверное, самое известное свойство конденсатора — накопление энергии. И действительно в простейшем случае конденсатор можно представить себе как некий накопитель, например, бочку для воды, у которой нас интересуют два параметра: высота и вместимость между двумя метками(условно разделим бочку метками параллельными основанию, причём расстояние между двумя метками у всех бочек одинаковое ). Высота бочки определяет максимальный уровень воды в бочке, а вместимость — количество воды, которое можно поместить между двумя меткам . Давайте рассмотрим конденсатор ёмкостью 1uF и максимальным напряжением 25V, на каждый вольт такого конденсатора приходится 1uF, а зарядить такой конденсатор можно до 25 вольт. Если мы зарядим такой конденсатор до 5V, в нём накопиться 5 раз по 1uF или 5uC(микрокулон, Q = C*U). Если же мы возьмём конденсатор 100V и 1uF и зарядим его до 5V, в нём также накопиться 5 раз по 1uF. Из этого можно сделать вывод, что низковольтный конденсатор можно запросто заменить более высоковольтным конденсатором такой же ёмкости. Как это можно использовать?Представьте себе микросхему, которая в определённые временные промежутки должна отдавать большой ток, причём за такой же промежуток времени она получает ток в несколько раз меньше, такой микросхеме для нормальной работы хорошо было бы под боком иметь бочонок с зарядом, роль такого бочонка, как раз и выполняет конденсатор и в таком случае он называется блокировочным или развязывающим. Развязывающим он называется потому, что как бы развязывает микросхему от общего питания и делает её в какой-то мере независимой от общего питания схемы. Что значит независимой от общего питания схемы?Представьте себе плату на, которой расположены две микросхемы, у одной есть блокировочный конденсатор, у другой нет. Если мы кратковременно отключим питание схемы, та микросхема у которой нет блокировочного конденсатора сразу перестанет работать, а микросхема у которой есть блокировочный конденсатор, будет работать еще некоторое время, пока конденсатор не разрядиться, в этом и проявляется её в какой-то мере независимость.Ёмкость блокировочного конденсатора обычно составляет 100nF и располагаться он должен как можно ближе к выводу микросхемы. Второе применение бочонка — сглаживание пульсаций.Представьте себе бочонок, в который вода подаётся и уходит как изображено на картинке ниже. Примерное соотношение для выбора такого конденсатора, 1000uF на 1А. Развязывающий конденсатор то же сглаживает пульсации, но основная его задача обеспечить запас энергии. Представляя конденсатор как бочку, очень просто понять параллельное соединение конденсаторов, если соединить два конденсатора параллельно, то их общая ёмкость будет равна сумме их ёмкостей. Следующие включение конденсатора связано с его способностью пропускать переменный ток и не пропускать постоянный. На просторах интернета можно найти такую картинку Ещё одно интересное свойство конденсатора — это скорость его зарядки. Также как вода не может мгновенно заполнить бочонок, также и конденсатор не может зарядиться мгновенно. Скорость заполнения бочонка ограничивает диаметр трубы, через которую подаётся вода, а скорость зарядки конденсатора ограничивает сопротивление, подключённое к одной из его обкладок. T = R*CПри последовательном соединении двух конденсаторов эквивалентная емкость равна 0,8 мкФ, а при параллельном - 5 мкФ. Определите емкость каждого конденсатора. Определите какой заряд способны накопить конденсаторы включенные по схеме
При последовательном соединении двух конденсаторов эквивалентная емкость равна 0,8 мкФ, а при параллельном
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Дано:
Решение:
С1,2=0,8 (пос)
С1,2=5 (пар) мкФ
Сэк = 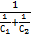 = 0,8 (пос.)
Сэк =С1+С2=5 (парал)
С1,2 = 0,8×5
С2 = (5-С2)=4
= 0,8 (пос.)
Сэк =С1+С2=5 (парал)
С1,2 = 0,8×5
С2 = (5-С2)=4
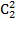 -5с2+4=0
С1=4; С2=1
С1=1; С2=4
-5с2+4=0
С1=4; С2=1
С1=1; С2=4
Найти:
С - ?
Ответ:
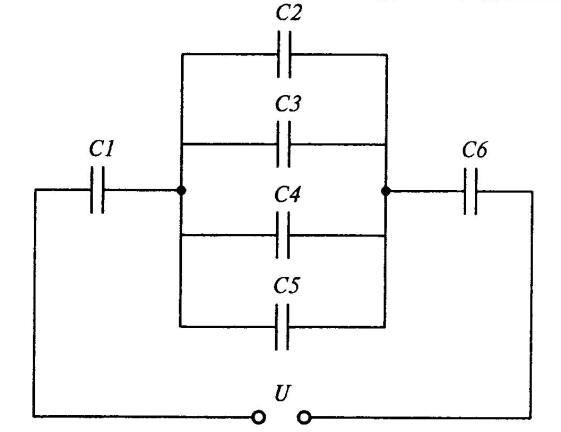
Дано:
Решение:
U = 350 В
С=0,5мкФ
=0,5×10-6Ф
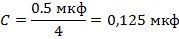 С=0,5мкФ×0,125мкФ+0,5мкФ=1,125мкФ
С=0,5мкФ×0,125мкФ+0,5мкФ=1,125мкФ
Найти:
Q - ?
Ответ:
1,125мкФ
Дано:
Решение:
U = 350 В
С=1,125*10-6 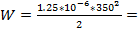 6.89 ДЖ
6.89 ДЖ
Найти:
W - ?
Ответ:
6,89дж
10 МОм
470 Ом
0,33 МОм
47 кОм
4700 Ом
1,5 кОм
1*10 7Ом
0,47кОм
330кОм
4,7×10-2Мом
4,7×10-3Мом
1500Ом
Дано:
Решение:
L= 200м
S =5мм2
P=1,3×10-7 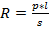
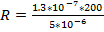 =5,20Ом
=5,20Ом
Найти:
R -?
Ответ:
5,20 ом
Дано:
Решение:
R-300м
S-0.21мм2
q-0.42
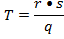
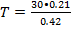 =15 м
=15 м
Найти:
T - ?
Ответ:
15 м
Дано:
Решение:
Q=1.1 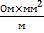 t-20
r-250
t-20
r-250
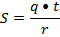
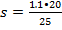 =0.88 мм2
=0.88 мм2
Найти:
S - ?
Ответ: 0,88 мм2 Дано:
Решение:
R=16 Ом
S=0.5 мм2
T=40 М
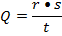
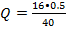 =0.2По таблицы удаленых сопротив. Находим, что таким сопротивлением обладает свинец.
=0.2По таблицы удаленых сопротив. Находим, что таким сопротивлением обладает свинец.
Найти:
Q - ?
Ответ:
0.2 свинец
 ; V=
; V= 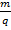
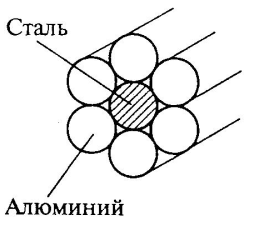 2.1.16. Провод состоит из одной стальной (ρ = 0,2410 Ом . м) и шести алюминиевых (ρ = 0,291 Ом . м) проволок диаметром 4,8 мм каждая. Определите сопротивление провода при температуре 20 0С.
2.1.16. Провод состоит из одной стальной (ρ = 0,2410 Ом . м) и шести алюминиевых (ρ = 0,291 Ом . м) проволок диаметром 4,8 мм каждая. Определите сопротивление провода при температуре 20 0С. Дано:
Решение:
D1=4.8мм=0.0048м
T=200C
q1=0,2410 Ом
q2= 0,291 Ом
R= 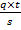 R=0.241
R=0.241
Найти:
R -?
Ответ: `0.241
Дано:
Решение:
R1 =2 Ом
R2 = 2,48 Ом
α = 0,004.
r2=r1[l + a ( t2-t1) ]
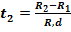 - t1
t2=
- t1
t2= 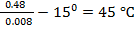
Найти:
T - ?
Ответ:
45℃
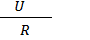 I =
I = 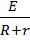
0,15 А
25 мА
140 мкА
0,02 А
1,7А
420 мкА
150 мА
2,5×104 мкА
0.00014А
20 мА
1700000мкА
0.42 мА
0,2 В
15 кВ
0,03 MB
25 мВ
1200 мкВ
220 В
200 мВ
15000 В
30кВ
25000мкВ
0.0012 В
0.22КВ
Дано:
Решение:
U-220 В
R-240 Ом
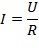 I=
I= 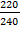 =0.91 A
=0.91 A
Найти:
I - ?
Ответ:
0.91A
При последовательном соединении двух конденсаторов эквивалентная емкость равна 0,8 мкФ, а при параллельном
Дано:
Решение:
С1,2=0,8 (пос)
С1,2=5 (пар) мкФ
Сэк = = 0,8 (пос.)
Сэк =С1+С2=5 (парал)
С1,2 = 0,8×5
С2 = (5-С2)=4
-5с2+4=0
С1=4; С2=1
С1=1; С2=4
Найти:
С - ?
Ответ:
Дано:
Решение:
U = 350 В
С=0,5мкФ
=0,5×10-6Ф
С=0,5мкФ×0,125мкФ+0,5мкФ=1,125мкФ
Найти:
Q - ?
Ответ:
1,125мкФ
Дано:
Решение:
U = 350 В
С=1,125*10-6 6.89 ДЖ
Найти:
W - ?
Ответ:
6,89дж
10 МОм
470 Ом
0,33 МОм
47 кОм
4700 Ом
1,5 кОм
1*10 7Ом
0,47кОм
330кОм
4,7×10-2Мом
4,7×10-3Мом
1500Ом
Дано:
Решение:
L= 200м
S =5мм2
P=1,3×10-7 =5,20Ом
Найти:
R -?
Ответ:
5,20 ом
Дано:
Решение:
R-300м
S-0.21мм2
q-0.42
=15 м
Найти:
T - ?
Ответ:
15 м
Дано:
Решение:
Q=1.1
t-20
r-250
=0.88 мм2
Найти:
S - ?
Ответ: 0,88 мм2 Дано:
Решение:
R=16 Ом
S=0.5 мм2
T=40 М
=0.2По таблицы удаленых сопротив. Находим, что таким сопротивлением обладает свинец.
Найти:
Q - ?
Ответ:
0.2 свинец
Дано:
Решение:
D1=4.8мм=0.0048м
T=200C
q1=0,2410 Ом
q2= 0,291 Ом
R=
R=0.241
Найти:
R -?
Ответ: `0.241
Дано:
Решение:
R1 =2 Ом
R2 = 2,48 Ом
α = 0,004.
r2=r1[l + a ( t2-t1) ]
- t1
t2=
Найти:
T - ?
Ответ:
45℃
0,15 А
25 мА
140 мкА
0,02 А
1,7А
420 мкА
150 мА
2,5×104 мкА
0.00014А
20 мА
1700000мкА
0.42 мА
0,2 В
15 кВ
0,03 MB
25 мВ
1200 мкВ
220 В
200 мВ
15000 В
30кВ
25000мкВ
0.0012 В
0.22КВ
Дано:
Решение:
U-220 В
R-240 Ом
I= =0.91 A
Найти:
I - ?
Ответ:
0.91A
Опыты с конденсаторами - Молодежный научно-технический центр
Недавно мы разобрались с резисторами, а теперь давайте займемся конденсаторами. КОНДЕНСАТОРЫ
Здесь мы рассмотрим теоретические основы работы и историю изобретения конденсатора. Как известно, конденсатор — своеобразный двухполюсник с определённым значением ёмкости и малой проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин, разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. 





Использование конденсатора в электронике. » Хабстаб
В электронике используются три основные свойства конденсатора:
В зависимости от схемы включения, какое-то из этих свойств может проявляться сильнее других. Если провести аналогию с конденсатором, то высота бочки определяет максимальное напряжение до которого можно зарядить конденсатор, зарядить конденсатор до большего напряжения не получится, аналогично тому, что вода из бочки начнёт выливаться, а конденсатор просто выйдет из строя, а то ещё и взорвётся. Вместимость между двумя метками, у конденсатора её называют ёмкостью, она определяет какой заряд приходится на 1 вольт, в этом случае расстояние между метками бочки в конденсаторе представляет собой разность потенциалов равную 1 вольт.
Если провести аналогию с конденсатором, то высота бочки определяет максимальное напряжение до которого можно зарядить конденсатор, зарядить конденсатор до большего напряжения не получится, аналогично тому, что вода из бочки начнёт выливаться, а конденсатор просто выйдет из строя, а то ещё и взорвётся. Вместимость между двумя метками, у конденсатора её называют ёмкостью, она определяет какой заряд приходится на 1 вольт, в этом случае расстояние между метками бочки в конденсаторе представляет собой разность потенциалов равную 1 вольт.
 Когда уровень воды в бочонке превысит уровень сливного отверстия, какие бы брызги ни происходили в бочонке, на выходе их видно не будет, такой конденсатор называют сглаживающим, его можно встретить после диодного моста.
Когда уровень воды в бочонке превысит уровень сливного отверстия, какие бы брызги ни происходили в бочонке, на выходе их видно не будет, такой конденсатор называют сглаживающим, его можно встретить после диодного моста. Ёмкость сглаживающего конденсатора — это отдельная тема, если она будет мала, то сглаживание будет происходить не полностью, а как на рисунке.
Ёмкость сглаживающего конденсатора — это отдельная тема, если она будет мала, то сглаживание будет происходить не полностью, а как на рисунке.
 она помогает запомнить это свойство конденсатора. Оно может пригодиться при работе со звуком, где полезным является только переменная составляющая сигнала, обозначенная на картинке синим цветом.
она помогает запомнить это свойство конденсатора. Оно может пригодиться при работе со звуком, где полезным является только переменная составляющая сигнала, обозначенная на картинке синим цветом. Такой конденсатор называют разделительным так как, он разделяет переменную и постоянную составляющую.
Такой конденсатор называют разделительным так как, он разделяет переменную и постоянную составляющую.
 Такое соединение конденсатора и резистора называют RC цепочкой, время зарядки конденсатора до 63% от приложенного напряжения легко посчитать по формуле
Такое соединение конденсатора и резистора называют RC цепочкой, время зарядки конденсатора до 63% от приложенного напряжения легко посчитать по формуле
И напоследок про последовательное соединение конденсаторов, в этом случае конденсатор удобно представить как смывной бачок унитаза. Представьте себе два бачка соединённых последовательно, но разных размеров, в которые подаётся вода. Механизмы, блокирующие подачу воды, в этих бочках соединены. Когда меньший бачок заполнится он заблокирует подачу воды, в другом бачке и получится такая ситуация: один бачок будет полный, а второй нет. Так же происходит при последовательном соединении двух конденсаторов, когда конденсатор с меньшей ёмкостью зарядиться, ток перестанет течь и конденсатор с большей ёмкостью больше заряжаться не будет. Оно и понятно, когда конденсатор с меньшей ёмкостью зарядиться, не будет разности потенциалов и как следствие, ток не потечёт.На этом всё.
hubstub.ru
Опыты с конденсаторами - is2006
Недавно мы разобрались с резисторами, а теперь давайте займемся конденсаторами.Конденсатор - это устройство для накопления заряда и энергии электрического поля. Конструктивно это «бутерброд» из двух проводников и диэлектрика, которым может быть вакуум, газ, жидкость, органическое или неорганическое твердое тело. Первые отечественные конденсаторы (стеклянные банки с дробью, обклеенные фольгой) делали в 1752 г. М. Ломоносов и Г. Рихтер.
Что может быть интересного в конденсаторе? Приступая к работе над этой статьей я думал что смогу собрать и кратко изложить все об этой примитивной детальке. Но по мере знакомства с конденсатором, я с удивлением понимал, что здесь не рассказать и сотой доли всех сокрытых в нем тайн и чудес…
Конденсатору уже более 250 лет, но он и не думает устаревать.. Кроме того, 1 кг «обычных просто конденсаторов» хранит меньше энергии чем килограмм аккумуляторов или топливных ячеек, но способен быстрее чем они выдать ее, развивая при этом большую мощность. - При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, импульсных лазерах с оптической накачкой и коллайдерах. Конденсаторы есть практически в любом приборе, поэтому если у вас нет новых конденсаторов, для опытов их можно выпаять оттуда.
Заряд конденсатора - это абсолютное значение заряда одной из его обкладок. Он измеряется в кулонах и пропорционален числу лишних (-) или недостающих (+) электронов. Чтобы собрать заряд в 1 кулон, Вам понадобится 6241509647120420000 электрона. В пузырьке водорода, размером со спичечную головку их примерно столько же.
Поскольку способность накапливать заряды у электрода ограничена их взаимным отталкиванием, их переход на электрод не может быть бесконечным. Словно любое хранилище, конденсатор имеет вполне определенную емкость. Так она и называется — электрическая емкость. Она измеряется в фарадах и для плоского конденсатора с обкладками площадью S (каждая), расположенными на расстоянии d, емкость равна Sε0ε/d (при S >> d), где ε – относительная диэлектрическая проницаемость, а ε0=8,85418781762039 * 10-12.Емкость конденсатора также равна q/U, где q – заряд положительной обкладки, U - напряжение между обкладками. Емкость зависит от геометрии конденсатора и диэлектрической проницаемости диэлектрика, и не зависит от заряда обкладок.
В заряженном проводнике заряды стараются разбежаться друг от друга как можно дальше и потому находятся не в толще конденсатора, а в поверхностном слое металла, подобно пленке бензина на поверхности воды. Если два проводника образуют конденсатор, то эти избыточные заряды собираются друг напротив друга. Потому практически все электрическое поле конденсатора сосредоточено между его обкладками.
На каждой обкладке заряды распределяются так, чтобы быть подальше от соседей. И расположены они довольно просторно: в воздушном конденсаторе с расстоянием между пластинами 1 мм, заряженном до 120 В, среднее расстояние между электронами составляет более 400 нанометров, что в тысячи раз больше расстояния между атомами (0,1-0,3 нм), а значит на миллионы поверхностных атомов приходится всего один лишний (или недостающий) электрон.
Если уменьшить расстояние между обкладками, то силы притяжения возрастут, и при том же напряжении заряды на обкладках смогут «ужиться» плотнее. Увеличится емкость конденсатора. Так и сделал ничего не подозревавший профессор Лейденского университета ван Мушенброк. Он заменил толстостенную бутылку первого в мире конденсатора (созданного немецким священником фон Клейстом в 1745 г.) тонкой стеклянной банкой. Зарядил ее и потрогал, а очнувшись через два дня сообщил, что не согласится повторить опыт, даже если бы за это обещали французское королевство.
Если поместить между обкладками диэлектрик, то они поляризуют его, то есть притянут к себе разноименные заряды из которых он состоит. При этом будет тот же эффект как если бы обкладки приблизились. Диэлектрик с высокой относительной диэлектрической проницаемостью можно рассматривать как хороший транспортер электрического поля. Но никакой транспортер не идеален, поэтому какой бы мы чудесный диэлектрик не добавили поверх уже имеющегося, емкость конденсатора только снизится. Повысить емкость можно только если добавлять диэлектрик (а еще лучше - проводник) вместо уже имеющегося но обладающего меньшей ε.
В диэлектриках свободных зарядов почти нет. Все они зафиксированы то ли в кристаллической решетке, или в молекулах – полярных (представляющих собой диполи) или нет. Если внешнего поля нет, диэлектрик неполяризован, диполи и свободные заряды разбросаны хаотически и диэлектрик собственного поля не имеет. в электрическом поле он поляризуется: диполи ориентируются по полю. Так как молекулярных диполей очень много, то при их ориентации, плюсы и минусы соседних диполей внутри диэлектрика компенсируют друг друга. Нескомпенсированными остаются только поверхностные заряды – на одной поверхности – одного, на другой - другого. Свободные заряды во внешнем поле также дрейфуют и разделяются.
При этом разные процессы поляризации идут с разной скоростью. Одно дело – смещение электронных оболочек, происходящее практически мгновенно, другое дело – поворот молекул, особенно больших, третье – миграция свободных зарядов. Последние два процесса, очевидно, зависят от темературы, и в жидкостях идут гораздо шустрее, чем в твердых телах. Если нагреть диэлектрик, повороты диполей и миграция зарядов ускорится. Если поле выключить, деполяризация диэлектрика происходит тоже не мгновенно. Он остается некоторое время поляризованным, пока тепловое движение не разбросает молекулы в исходное хаотическое состояние. Поэтому, для конденсаторов, где переключается полярность с высокой частотой пригодны только неполярные диэлектрики: фторопласт, полипропилен.
Если разобрать заряженный конденсатор, а потом собрать (пластмассовым пинцетом), энергия никуда не денется, и светодиод сможет моргнуть. Он даже моргнет если подключить его к конденсатору в разобранном состоянии. Оно и понятно – при разборке заряд с пластин никуда не делся, а напряжение даже выросло, поскольку уменьшилась емкость и теперь обкладки прямо-таки распирает от зарядов. Стоп, как это напряжение выросло, ведь тогда вырастет и энергия? Так и есть, мы же сообщили системе механическую энергию, преодолевая кулоновское притяжение обкладок. Собственно, в этом и фишка электризации трением – зацепить электроны на расстоянии порядка размеров атомов и оттащить на макроскопическое расстояние, тем самым повысив напряжение с нескольких вольт (а таково напряжение в химических связях) до десятков и сотен тысяч вольт. Теперь понятно, почему синтетическая кофта бьется током не когда ее носишь, а только когда ее снимаешь? Стоп, а почему не до миллиардов? Дециметр же в миллиард раз больше ангстрема, на котором мы урвали электроны? Да потому что работа по перемещению заряда в электрическом поле равна интегралу Eq по d и это самое E ослабевает с расстояние квадратично. А если бы на всем дециметре между кофтой и носом было такое же поле как внутри молекул, то щелкнул бы по носу и миллиард вольт.
Проверим это явление – повышение напряжения при растягивании конденсатора – экспериментально. Я написал простую программку на Visual Basic для приема данных с нашего контроллера ПМК018 и вывода их на экран. В общем, берем две 200х150 мм пластины текстолита, покрытого с одной стороны фольгой и припаиваем проводки, идущие к измерительному модулю. Затем кладем на одну из них диэлектрик – лист бумаги – и накрываем второй пластиной. Пластины прилегают неплотно, поэтому придавим их сверху корпусом авторучки (если давить рукой, то можно создать помехи).
Схема измерения простая: потенциометр R1 устанавливает напряжение (в нашем случае это 3 вольта), подаваемое на конденсатор, а кнопка S1 служит для того чтобы подавать его на конденсатор, или не подавать.
Итак, нажмем и отпустим кнопку – мы увидим график, показанный слева. Конденсатор быстро разряжается через вход осциллографа. Теперь попробуем во время разряда ослабить давление на пластины – увидим пик напряжения на графике (справа). Это как раз искомый эффект. При этом расстояние между обкладками конденсатора растет, емкость падает и потому конденсатор начинает разряжаться еще быстрее.
Тут я не на шутку задумался.. Кажется, мы на пороге великого изобретения…Ведь если при раздвигании обкладок на них растет напряжение, а заряд остается прежним, то можно ведь взять два конденсатора, на одном раздвигать на них обкладки, а в точке максимального раздвижения передать заряд неподвижному конденсатору. Потом вернуть обкладки на место и повторить то же самое наоборот, раздвигая другой конденсатор. По идее напряжение на обоих конденсаторах будет расти с каждым циклом в определенное число раз. Отличная идея для электрогенератора! Можно будет создать новые конструкции ветряков, турбин и всего такого! Так, прекрасно… для удобства можно разместить все это на двух дисках, вращающихся в противоположные стороны…. ой что же это… тьфу, это же школьная электрофорная машина! :(
В качестве генератора она не прижилась, так как неудобно иметь дело с такими напряжениями. Но на наноуровне все может измениться. Магнитные явления в наноструктурах во много раз слабее электрических, а электрические поля там, как мы уже убедились, огромны, поэтому молекулярная электрофорная машина может стать весьма популярной.
Конденсатор как хранитель энергии
Убедиться, что в самом ничтожнейшем конденсаторе хранится энергия очень легко. Для этого нам понадобится прозрачный светодиод красного свечения и источник постоянного тока (батарейка 9 вольт подойдет, но если номинальное напряжение конденсатора позволяет, лучше взять побольше). Опыт заключается в том чтобы зарядить конденсатор, а потом подключить к нему светодиод (не забываем про полярность), и смотреть как он моргнет. В темной комнате видна вспышка даже от конденсаторов в десятки пикофарад. Это каких-нибудь сто миллионов электронов испускают сто миллионов фотонов. Впрочем это не предел, ведь человеческий глаз может замечать куда более слабый свет. Просто я не нашел еще менее ёмких конденсаторов. Если же счет пошел на тысячи микрофарад, пожалейте светодиод, а вместо этого замыкайте конденсатор на металлический предмет чтобы увидеть искру – очевидное свидетельство наличия в конденсаторе энергии.
Энергия заряженного конденсатора ведет себя во многом подобно потенциальной механической энергии - энергии сжатой пружины, поднятого на высоту груза или водонапорного бачка (а энергия катушки индуктивности, наоборот, подобна кинетической). Способность конденсатора накапливать энергию издавна применяется для обеспечения непрерывной работы устройств при кратковременных спадах питающего напряжения – от часов до трамваев.
Конденсатор также используется для накопления «почти вечной» энергии, вырабатываемой тряской, вибрацией, звуком, детектированием радиоволн или излучения электросетей. Мало-помалу накопленная энергия от таких слабых источников в течение долгого времени позволяет затем некоторое время работать беспроводным датчикам и другим электронным приборам. На этом принципе основана вечная «пальчиковая» батарейка для устройств со скромным энергопотреблением (вроде ТВ пультов). В ее корпусе находится конденсатор емкостью 500 миллифарад и генератор, подпитывающий его при колебаниях с частотой 4–8 герц дармовой мощностью от 10 до 180 милливатт. Разрабатываются генераторы на основе пьезоэлектрических нанопроводков, способные направлять в конденсатор энергию таких слабых вибраций, как биения сердца, удары подошв обуви по земле, и вибрации технического оборудования.
Еще один источник дармовой энергии – торможение. Обычно при торможении транспорта энергия переходит в тепло, а ведь ее можно сохранить и затем использовать при разгоне. Особенно остро стоит эта проблема для общественного транспорта, который тормозит и разгоняется у каждой остановки, что ведет к значительному расходу топлива и загрязнению атмосферы выхлопами. В Саратовской области в 2010 г. фирмой «Элтон» создан «Экобус» - экспериментальная маршрутка с необычными электродвигателями «мотор-колесо» и суперконденсаторами – накопителями энергии торможения, снижающими энергопотребление на 40%. Там применены материалы, разработанные в проекте «Энергия-Буран», в частности, углеродная фольга. Вообще, благодаря созданной еще в СССР научной школе, Россия является одним из мировых лидеров в сфере разработки и производства электрохимических конденсаторов. Например, продукция «Элтона» экспортируется за рубеж с 1998 года, а недавно в США началось производство этих изделий по лицензии российской компании.
Емкость одного современного конденсатора (2 фарады, фото слева) в тысячи раз превышает емкость всего земного шара. Они способны хранить электрический заряд в 40 Кулон!
Используются они, как правило, в автомобильных аудиосистемах, чтобы снизить пиковую нагрузку на электропроводку автомобиля (в моменты мощных бас-ударов) и за счёт огромной ёмкости конденсатора подавить все высокочастотные помехи в бортовой сети.
А вот этот советский «дедушкин сундучок» для электронов (фото справа) не столь емок, но зато выдерживает напряжение в 40.000 вольт (обратите внимание на фарфоровые чашечки, защищающие все эти вольты от пробоя на корпус конденсатора). Это очень удобно для «электромагнитной бомбы», в которой конденсатор разряжается на медную трубочку, которая в тот же момент сжимается снаружи взрывом. Получается очень мощный электромагнитный импульс, выводящий из строя радиоаппаратуру. Кстати, при ядерном взрыве, в отличие от обычного, тоже выделяется электромагнитный импульс, что еще раз подчеркивает сходство уранового ядра с конденсатором. Кстати, такой конденсатор вполне можно напрямую зарядить статическим электричеством от расчески, только конечно заряжать до полного напряжения придется долго. Зато можно будет повторить печальный опыт ван Мушенброка в очень усугубленном варианте.
Если просто потереть об волосы авторучку (расческу, воздушный шарик, синтетическое белье и т.п.), то светодиод от нее гореть не будет. Это потому, что избыточные (отнятые у волос) электроны заневолены каждый в своей точке на поверхности пластика. Поэтому если даже мы и попадем выводом светодиода в какой-то электрон, другие не смогут устремиться за ним и создать нужный для заметного невооруженным глазом свечения светодиода ток. Другое дело, если перенести заряды с авторучки в конденсатор. Для этого возьмем конденсатор за один вывод и буде тереть авторучку по очереди то о волосы, то о свободный вывод конденсатора. Почему именно тереть? Чтобы по максимуму собрать урожай электронов со всей поверхности ручки! Несколько раз повторим этот цикл и подключим к конденсатору светодиод. Он моргнет, причем только при соблюдении полярности. Так конденсатор стал мостиком между мирами «статического» и «обычного» электричества :)
Я взял для этого опыта высоковольтный конденсатор, опасаясь пробоя низковольтного, но оказалось, что это излишняя предосторожность. При ограниченной подаче заряда напряжение на конденсаторе может быть намного меньше напряжения источника питания. Конденсатор может преобразовывать большое напряжение в малое. Например, статическое высоковольтное электричество – в обычное. В самом деле, есть ли разница: зарядить конденсатор одним микрокулоном от источнка напряжением 1 В или 1000 В? Если этот конденсатор настолько емкий, что от заряда в 1 мкКл на нем напряжение не повысится выше напряжения одновольтового источника питания (т.е. емкость его выше 1 мкф), то разницы нет. Просто если не ограничивать принудительно кулоны, то от высоковольного источника их захочет прибежать больше. Да и тепловая мощность, выделившаяся на выводах конденсатора будет больше (а количество теплоты то же, просто оно быстрее выделится, оттого и мощность больше).
В общем, видимо, для этого опыта годится любой конденсатор емкостью не более 100 нф. Можно и более, но понадобится долго его заряжать чтобы получить достаточное для светодиода напряжение. Зато, если токи утечки в конденсаторе невелики, светодиод будет гореть дольше. Можно подумать о создании на этом принципе устройства подзарядки сотового телефона от трения его об волосы во время разговора :)
Отличным высоковольтным конденсатором является отвертка. При этом ручка ее служит диэлектриком, а металлический стержень и рука человека – обкладками. Мы знаем, что натертая об волосы авторучка притягивает клочки бумаги. Если натирать об волосы отвертку то ничего не выйдет – металл не обладает способностью отнимать электроны у белков – она как не притягивала бумажки, так и не стала. Но если как в предыдущем опыте тереть ее заряженной авторучкой – отвертка, вследствие своей малой емкости, быстро заряжается до высокого напряжения и бумажки начинают к ней притягиваться.
Светится от отвертки и светодиод. На фото нереально поймать краткий миг его вспышки. Но - вспомним свойства экспоненты - угасание-то вспышки длится долго (по меркам затвора фотоаппарата). И вот мы стали свидетелями уникального лингвистико-оптико-математического явления: экспонента экспонировала-таки матрицу фотоаппарата!Впрочем, к чему такие сложности - есть же видеосъемка. На ней видно, что вспыхивает светодиод довольно ярко:
Когда конденсаторы заряжают до высоких напряжений, начинает играть свою роль краевой эффект, состоящий в следующем. Если диэлектрик на воздухе поместить между обкладками и приложить к ним постепенно повышающееся напряжение, то при некотором значении напряжения на краю обкладки возникает тихий разряд, обнаруживаемый по характерному шуму и свечению в темноте. Величина критического напряжения зависит от толщины обкладки, остроты края, рода и толщины диэлектрика и пр. Чем диэлектрик толще, тем выше кр. Например, чем диэлектрическая постоянная диэлектрика выше, тем оно ниже. Для уменьшения краевого эффекта края обкладки заделывают в диэлектрик с высокой электрической прочностью, утолщают диэлектрик прокладку на краях, закругляют края обкладок, создают на краю обкладок зону с постепенно падающим напряжением за счет изготовления краев обкладок из материала с высоким сопротивлением, уменьшением напряжения, приходящегося на один конденсатор путем разбивки его на несколько последовательно включенных.
Вот почему отцы-основатели электростатики любили чтобы на конце электродов были шарики. Это, оказывается, не дизайнерская фишка, а способ максимально уменьшить стекание заряда в воздух. Дальше уже некуда. Если кривизну какого-то участка на поверхности шарика еще уменьшить,то неизбежно возрастет кривизна соседних участков. Да и тут по-видимому в наших электростатических делах важна не средняя а максимальная кривизна поверхности, которая минимальна, конечно у шарика.
Хм.. но если емкость тела это способность накапливать заряд, то она, наверное, весьма различна для положительных и отрицательных зарядов…. Представим себе сферический конденсатор в вакууме… От души зарядим его отрицательно, не жалея электростанций и гигаватт-часов (вот чем хорош мысленный эксперимент!)… но в какой-то момент избыточных электронов станет на этом шаре так много, что они попросту начнут разлетаться по всему вакууму, лишь бы не находиться в такой электроотрицательной тесноте. А вот с положительным зарядом такого не произойдет – электроны, как бы их мало не осталось, никуда из кристаллической решетки конденсатора не улетят.
Что же получается, положительная емкость заведомо намного больше отрицательной? Нет! Потому что электроны там вообще-то были не для нашего баловства, а для соединения атомов, и без сколь-нибудь заметной их доли, кулоновское отталкивание положительных ионов кристаллической решетки мгновенно разнесет в пыль самый бронированный конденсатор :)
На самом же деле, без вторичной обкладки, емкость «уединенных половинок» конденсатора очень мала: электроемкость уединенного куска провода диаметром 2 мм и длиной 1 м равна приблизительно 10 пФ, а всего земного шара – 700 мкф.
Можно построить абсолютный эталон емкости, рассчитав его емкость по физическим формулам исходя из точных измерений размеров обкладок. Так и сделаны самые точные конденсаторы в нашей стране, которые находятся в двух местах. Государственный эталон ГЭТ 107-77 находится в ФГУП СНИИМ и состоит из 4-х безопорных коаксиально-цилиндрических конденсаторов, емкость которых рассчитывается с высокой точностью через скорость света и единицы длины и частоты, а также высокочастотного емкостного компаратора, позволяющего сравнивать емкости приносимых на поверку конденсаторов с эталоном (10 пф) с погрешностью менее 0,01% в диапазоне частот 1-100 МГц (фото слева).
Эталон ГЭТ 25-79 (фото справа), находящийся в ФГУП ВНИИМ им. Д.И. Менделеева содержит расчетный конденсатор и интерферометр в вакуумном блоке, емкостный трансформаторный мост в комплекте с мерами емкости и термостатом и источники излучения со стабилизированной длиной волны. В основу эталона положен метод определения приращений емкости системы перекрестных электродов расчетного конденсатора при изменении длины электродов на заданное количество длин волн высокостабильного светового излучения. Это обеспечивает поддержание точного значения емкости 0,2 пф с точностью выше 0,00005 %
Но на радиорынке в Митино я затруднился найти конденсатор с точностью выше 5% :( Что ж, попробуем рассчитать емкость по формулам на основе измерений напряжения и времени через наш любимый ПМК018. Будем рассчитывать емкость двумя способами. Первый способ основан на свойствах экспоненты и отношении напряжений на конденсаторе, измеренных в разные моменты разряда. Второй - на измерении заряда, отданного конденсатором при разряде, он получается интегрированием тока по времени. Площадь, ограниченная графиком тока и осями координат, численно равна заряду, отданному конденсатором. Для этих расчетов нужно точно знать сопротивление цепи через которую разряжается конденсатор. Это сопротивление я задал прецизионным резистором на 10 кОм из электронного конструктора.
И вот результаты эксперимента. Обратите внимание на то какая красивая и гладкая получилась экспонента. Она ведь не математически рассчитана компьютером, а непосредственно измерена из самой природы. Благодаря координатной сетке на экране видно, что точно соблюдается свойство экспоненты - через равные промежутки времени уменьшаться в равное количество раз (я даже линейкой мерил на экране :) Таким образом, мы видим, что физические формулы вполне адекватно отражают окружающую нас реальность.
Как видим, измеренная и рассчитанная емкость приблизительно совпадает с номинальной (и с показаниями китайских мультиметров), но не точь-в-точь. Жаль, что нет эталона, чтобы определить какая из них все-таки истинна! Если кто-нибудь знает эталон емкости, недорогой или доступный в быту – обязательно напишите об этом здесь, в комментариях.
В силовой электротехнике первым в мире применил конденсатор Павел Николаевич Яблочков в 1877 г. Он упростил и вместе с тем усовершенствовал конденсаторы Ломоносова, заменив дробь и фольгу жидкостью, и соединив банки параллельно. Ему принадлежит не только изобретение инновационных дуговых ламп, покоривших Европу, но и ряд патентов, связанных с конденсаторами. Попробуем собрать конденсатор Яблочкова, используя подсоленную воду в качестве проводящей жидкости, а в качестве банки – стеклянную банку из по овощей. Получилась емкость 0,442 нф. Заменим банку полиэтиленовым пакетом, имеющим большую площадь и во много раз меньшую толщину – емкость вырастет до 85,7 нф. (Сначала наполним пакет водой и проверим, нет ли токов утечки!) Конденсатор работает – даже позволяет моргнуть светодиодом! Он также успешно выполняет свои функции в электронных схемах (я попробовал его включить в генератор вместо обычного конденсатора - все работает).
Вода тут играет весьма скромную роль проводника, и если есть фольга, то можно обойтись без нее. Так сделаем, вслед за Яблочковым, и мы. Вот конденсатор из слюды и медной фольги, емкостью 130 пф.
Металлические обкладки должны возможно плотно прилегать к диэлектрику, причем надо избегать введения между обкладкой и диэлектриком клеящего вещества, которое вызовет добавочные потери на переменном токе. Поэтому теперь в качестве обкладок применяют главным образом металл, химически или механически осажденный на диэлектрик (стекло) или плотно припрессованный к нему (слюда).
Можно вместо слюды использовать кучу разных диэлектриков, каких угодно. Измерения (для диэлектриков равной толщины) показали, что у воздуха ε самое маленькое, у фторопласта побольше, у силикона еще больше, а у слюды даже еще больше , а у цирконат-титаната свинца оно просто огромно. Именно так по науке и должно быть – ведь во фторопласте электроны, можно сказать, намертво прикованы фтороуглеродными цепями и могут лишь чуть-чуть отклониться – там даже с атома на атом электрону некуда перескочить.Вы можете сами провести такие опыты с веществами, имеющими разную диэлектрическую проницаемость. Как вы думаете, что имеет большую диэлектрическую проницаемость, дистиллированная вода или масло? Соль или сахар? Парафин или мыло? Почему? Диэлектрическая проницаемость зависит много от чего... про нее можно было бы написать целую книгу.
Продолжение статьи - здесь.is2006.livejournal.com
Для чего нужен конденсатор и как он работает
Конденсатор (от латинского слова «condensare» — «уплотнять», «сгущать») — это двухполюсное устройство с определённой величиной или переменным значением ёмкости и малой проводимостью, которое способно сосредотачивать, накапливать и отдавать другим элементам электрической цепи заряд электрического тока.
Конденсатор или как его еще называют сокращенно просто «кондер» — это элемент электрической цепи, состоящий в самом простом варианте из двух электродов в форме пластин (или обкладок), которые накапливают противоположные разряды и поэтому они разделены между собой диэлектриком малой толщины по сравнению с размерами самих электропроводящих обкладок. На практике же, все выпускаемые конденсаторы представляют собой многослойные рулоны лент электродов в форме цилиндра или параллелепипеда, разделенных между собой слоями диэлектрика.
На практике же, все выпускаемые конденсаторы представляют собой многослойные рулоны лент электродов в форме цилиндра или параллелепипеда, разделенных между собой слоями диэлектрика.
Принцип работы конденсатора
По принципу работы он схож с батарейкой только на первый взгляд, но все же он сильно отличается от него по принципу и скорости заряда-разряда, максимальной емкости.
Заряд конденсатора. В момент подключения к источнику питания оказывается больше всего места на электродах, поэтому и ток будет зарядки максимальным, но по мере накопления заряда, ток будет уменьшаться и пропадет полностью после полного заряда. При зарядке на одной пластине будут собираться отрицательно заряженные частицы- электроны, а на другой – ионы, положительно заряженные частицы. Диэлектрик выступает препятствием для их перескакивания на противоположную сторону конденсатора. При зарядке растет и напряжение с нуля перед началом зарядки и достигает в самом конце максимума, равного напряжению источника питания.
При зарядке растет и напряжение с нуля перед началом зарядки и достигает в самом конце максимума, равного напряжению источника питания.
Разрядка конденсатора. Если после окончания зарядки отключить источник питания и подключить нагрузку R, то он сам превратится в источник тока. При подключении нагрузки образовывается цепь между пластинами. Отрицательно заряженные электроны двинуться через нагрузку к положительно заряженных ионам на другой пластине по закону притяжения между разноименными зарядами. В момент подключения нагрузки, начальный ток по закону Ома будет равняться величине напряжения на электродах (равного в конце зарядке конденсатора напряжению источника питания), разделенному на сопротивление нагрузки.После того как пошел ток, конденсатор начинает постепенно терять заряд или разряжаться. Одновременно с этим начнет снижаться величина напряжения, соответственно по закону Ома и ток. В то же время чем выше уровень разряда обкладок, тем ниже будет скорость падения напряжения и силы тока. Процесс завершится после того, как напряжение на электродах конденсатора станет равно нулю.
В момент подключения нагрузки, начальный ток по закону Ома будет равняться величине напряжения на электродах (равного в конце зарядке конденсатора напряжению источника питания), разделенному на сопротивление нагрузки.После того как пошел ток, конденсатор начинает постепенно терять заряд или разряжаться. Одновременно с этим начнет снижаться величина напряжения, соответственно по закону Ома и ток. В то же время чем выше уровень разряда обкладок, тем ниже будет скорость падения напряжения и силы тока. Процесс завершится после того, как напряжение на электродах конденсатора станет равно нулю.
Время зарядки конденсатора на прямую зависит от величины его емкости. Чем большей она величины, тем дольше будет проходить по цепи большее количество заряда.
Время разрядки зависит от величины подключенной нагрузки. Чем больше подключено сопротивление R, тем меньше будет ток разрядки.
Для чего нужен конденсатор
Конденсаторы широко используются во всех электронных и радиотехнических схемах. Они вместе с транзисторами и резисторами являются основой радиотехники.
Применение конденсаторов в электротехнических устройствах и бытовой технике:
- Важным свойством конденсатора в цепи переменного тока является его способность выступать в роли емкостного сопротивления (индуктивное у катушки). Если подключить последовательно конденсатор и лампочку к батарейке, то она не будет светиться. Но если подключить к источнику переменного тока, то она загорится. И светиться будет тем ярче, чем выше емкость конденсатора. Благодаря этому свойству они широко применяются в качестве фильтра, который способен довольно успешно подавлять ВЧ и НЧ помехи, пульсации напряжения и скачки переменного тока.
- Благодаря способности конденсаторов долгое время накапливать заряд и затем быстро разряжаться в цепи с малым сопротивлением для создания импульса, делает их незаменимыми при производстве фотовспышек, ускорителей электромагнитного типа, лазеров и т. п.
- Способность конденсатора накапливать и сохранять электрический заряд на продолжительное время, сделало возможным использование его в элементах для сохранения информации. А так же в качестве источника питания для маломощных устройств. Например, пробника электрика, который достаточно вставить в розетку на пару секунд пока не зарядится в нем встроенный конденсатор и затем можно целый день прозванивать цепи с его помощью. Но к сожалению, конденсатор значительно уступает в способности накапливать электроэнергию аккумуляторной батареи из-за токов утечки (саморазряда) и неспособности накопить электроэнергию большой величины.
- Конденсаторы используются при подключении электродвигателя 380 на 220 Вольт. Он подключается к третьему выводу, и благодаря тому что он сдвигает фазу на 90 градусов на третьем выводе- становится возможным использования трехфазного мотора в однофазной сети 220 Вольт.
- В промышленности конденсаторные установки применяются для компенсации реактивной энергии.
В следующей статье мы рассмотрим подробно основные характеристики и типы конденсаторов.
olimp23.com













Поделиться с друзьями: