Знание физики и теории этой науки напрямую связано с ведением домашнего хозяйства, ремонтом, строительство и машиностроением. Предлагаем рассмотреть, что такое резонанс токов и напряжений в последовательном контуре RLC, какое основное условие его образования, а также расчет. Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура. Признаки резонанса: Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов: Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления. Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость. Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему. Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот. Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика. Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма: Переключатель будет отвечать за направление колебаний. Конденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров. Направленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора. Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат. Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять. В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще. Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои. Нужно отметить, что это явление требует весьма тщательного расчета, особенно, если используется параллельное соединение. Для того чтобы в технике не возникали помехи, нужно использовать различные формулы. Они же Вам пригодятся для решения любой задачи по физике из соответствующего раздела. Очень важно знать, значение мощности в цепи. Средняя мощность, рассеиваемая в резонансном контуре, может быть выражена в терминах среднеквадратичного напряжения и тока следующим образом: R ср= I2конт * R = (V2конт / Z2) * R. При этом, помните, что коэффициент мощности при резонансе равен cos φ = 1 Сама же формула резонанса имеет следующий вид: ω0 = 1 / √L*C Нулевой импеданс в резонансе определяется при помощи такой формулы: Fрез = 1 / 2π √L*C Резонансная частота колебаний может быть аппроксимирована следующим образом: F = 1/2 р (LC) 0.5 Где: F = частота L = индуктивность C = емкость Как правило, схема не будет колебаться, если сопротивление (R) не является достаточно низким, чтобы удовлетворять следующим требованиям: R = 2 (L / C) 0.5 Для получения точных данных, нужно стараться не округлять полученные значения вследствие расчетов. Многие физики рекомендуют использовать метод, под названием векторная диаграмма активных токов. При правильном расчете и настройке приборов, у Вас получится хорошая экономия переменного тока. www.asutpp.ru В процессе изучения электротехники довольно часто возникает вопрос, что такое резонанс токов. Подобное явление характерно в основном для цепей переменного тока и может обладать как полезными, так и нежелательными свойствами, которые следует учитывать при проектировании различных схем. Явление резонанса часто применяется в радиотехнике. Настройка колебательного контура, связанного с этим свойством, дает возможность усиления радиосигнала в несколько раз, поскольку преобразование емкости-индуктивности приводит к возрастанию действующего напряжения. Наглядное представление о резонансе токов дает колебательный контур, применяемый в электронных схемах. В его состав входит конденсатор с емкостью С и катушка с индуктивностью L, включенные параллельно. В процессе передачи энергии из электрического поля емкости в магнитное поле индуктивности возникают самозатухающие колебания с определенной частотой. Возникновение колебаний происходит благодаря активному сопротивлению R, препятствующему свободному прохождению тока. Явление резонанса токов появляется в цепи, куда параллельно включены конденсатор и катушка. Их номиналы подобраны с таким расчетом, чтобы токи, протекающие по С и L, были равны. Поэтому в контуре С-L ток будет выше, чем его значение на остальных участках цепи. Принцип работы такого контура заключается в следующем. При подаче питания конденсатор накапливает определенную величину заряда, равную номинальному напряжению источника тока. После этого источник отключается, а конденсатор замыкается в цепь контура, чтобы на катушку пошел разряд. Ток проходит по ней, тем самым вызывает генерацию магнитного поля. В результате создается электродвижущая сила самоиндукции, направленная навстречу току. Максимальное значение магнитного поля достигается при полном разряде конденсатора. Таким образом, вся энергия, накопленная конденсатором, преображается в магнитное поле индуктивности. Заряженные частицы продолжают двигаться, благодаря самоиндукции катушки. Поскольку противоток от разряженного конденсатора уже отсутствует, он подвергается повторной зарядке, но уже с изменившейся полярностью. Это приводит к преобразованию поля катушки в заряд конденсатора и повторению всего процесса. Активная составляющая R приводит к постепенному угасанию колебаний. В этом и заключается основная суть резонанса. Резонанс токов широко используется на практике. В случае изменения величины емкости конденсатора или индуктивности контура, становится возможной регулировка частоты свободных колебаний. Таким образом, контур может быть настроен на определенную частоту. Природа свободных электрических колебаний, возникающих в контуре, всегда затухающая. Колебания затухают постепенно под влиянием сопротивления, которым обладают соединительные провода. Кроме того, энергия затрачивается на нагрев провода катушки индуктивности при прохождении в контуре электрического тока. Потери энергии приводят к постепенному снижению амплитуды колебаний и их окончательное затухание. Сопротивление контура оказывает непосредственное влияние на скорость затухания колебаний, связанную с потерями энергии. Для электронных устройств очень важно иметь возможность получения незатухающих электрических колебаний с неизменной амплитудой в течение продолжительного времени. Для обеспечения этого процесса выполняется подключение к контуру генератора переменного тока. В результате, частота вынужденных колебаний не будет зависеть от емкости и индуктивности контура, а будет находится в зависимости от частоты переменного тока, вырабатываемого генератором. Необходимо соблюдать условия, когда токи в емкости и индуктивности имели бы одинаковое значение. Это важное свойство дает возможность регулировок на любых участках электронных схем. electric-220.ru Цель работы: 1) изучить процессы в цепи переменного тока, состоящей из последовательно соединенных катушки и конденсатора; 2) изучить явление резонанса напряжений и условия, при которых оно наблюдается; 3) освоить методику построения векторных диаграмм для цепи с последовательным соединением элементов. Приборы и оборудование Работа выполняется на универсальном стенде, где установлен лабораторный автотрансформатор (ЛАТР) и необходимые приборы. Индуктивная катушка и батарея конденсаторов с регулируемой (с помощью выключателей) емкостью находятся на столе. Электрическая цепь собирается с помощью комплекта проводов в соответствии со схемой соединений (рис.1). Контрольные вопросы Ответ 1: Каждое ЭТ устройство заменяют его условным (согласно ГОСТ) изображением. Такие схемы называютсяпринципиальными.Принципиальная схема лабораторной установки представлена на рис.1. Рис.1 Для количественного расчета цепи необходимо иметь схему замещения. В схеме замещения ЭТ устройство заменяют ее идеальным образом, передающим его основные свойства (электрические и энергетические характеристики). Так как индуктивная катушка обладает активным и индуктивным сопротивлениями, то на схеме замещения этой цепи (рис.2), катушка представлена в виде 2-х последовательно соединенных элементов -резистора R и индуктивности L , а батарея конденсаторов - емкостным элементом С. Измерительные приборы (амперметр, вольтметры, ваттметр) в схеме замещения не представлены, т.к. они потребляют незначительную по сравнению с вышеуказанными элементами мощность и незначительно влияют на электрические характеристики цепи. Рис. 2 Сопротивление катушки R обусловлено сопротивлением провода катушки индуктивности. При прохождении через него тока I оно нагревается и на нем выделяется мощность: . При прохождении через катушку индуктивности L тока I вокруг нее образуется магнитное поле. Катушка накапливает магнитную (реактивную) энергию. Соответствующая мощность равна: , где. При прохождении тока через емкостной элемент С в нем образуется электрическое поле. Емкость накапливает электрическую (реактивную) энергию. Соответствующая мощность равна:,где. Ответ 2.1: Из схемы замещения следует, что электрическая цепь состоит из 3-х последовательно соединенных сопротивлений: . Полное сопротивление следовало бы считать равным сумме сопротивлений. Однако т.к. в цепях переменного тока реактивные элементы влияют на сдвиг фаз между током и напряжением на этом элементе, сопротивления заменяют их комплексными образами и полное сопротивление рассчитывают как сумму комплексных сопротивлений: ; Величина (модуль) полного сопротивления равна: ; При резонансе напряжений . Поэтому . Реактивные сопротивления друг друга компенсируют, полное сопротивлениестановится чисто активным и равным сопротивлению катушки. Ответ 2.2. Из анализа схемы замещения (из 2-го закона Кирхгофа) следует, что: При резонансе напряжений С и , поэтому ток равен :. Вывод: При резонансе ток в цепи и определяется только отношением входного напряжения к чисто активному сопротивлению катушки. Ответ 2.3 В цепи переменного тока различают активную , реактивнуюи полнуюмощность, которые рассчитываются следующим образом: , Вт; , ВАр; , ВА. Реактивная составляющая полной мощности цепи находится как разность индуктивной QL и емкостной QC ее составляющих: Коэффициент мощности электрической цепи cosφ показывает долю активной мощности Р в полной мощности цепи S: . Полная мощность рассчитывается по формуле: . Вариант ответа a) При резонансе напряжений: cosφ0=Р0/UI0. Но Р0 =I02R , U=I0·R. После подстановки в выражение для cosφ0 имеем: . Вариант b) При резонансе суммарная реактивная мощность равна нулю , поэтому полная мощность S равна чисто активной мощности P. Следовательно: . Вывод: При резонансе напряжений +коэффициент мощности , т.е. вся подводимая мощность расходуется только на нагрев проводов катушки индуктивности. **) можно определить из соотношения studfiles.net Цель работы: Установление условий резонанса напряжений. Исследование частотных зависимостей напряжений на элементах последовательного резонансного контура. Домашнее задание Укажите необходимые и достаточные условия для возникновения в электрических цепях переменного синусоидального тока резонанса напряжений. Охарактеризуйте возможные способы получения резонанса напряжений в электрической цепи. Приведите расчетные соотношения для определения значений искомых величин при резонансе напряжений. Каким образом можно обнаружить резонанс напряжений? Что представляет собой амплитудно-частотная характеристика (АЧХ) последовательного резонансного контура? Каким способом по АЧХ можно определить полосу пропускания (прозрачности) контура? Что представляет собой фазочастотная характеристика (ФЧХ) последовательного резонансного контура? Почему идеальная ФЧХ в полосе пропускания должна быть линейной? Резонансом напряжений называется режим, при котором в электрической цепи (рис. 1) с последовательным соединением индуктивного и емкостного элементов напряжение на входе цепи совпадает по фазе с током. При резонансе напряжений характерна возможность возникновения равных по модулю и противоположных по фазе действующих значений напряжений на катушке индуктивности и конденсаторе, существенно превышающих действующее значение напряжения на входе цепи. Отсюда название режима работы цепи – резонанс напряжений. Для последовательного резонансного контура входное сопротивление контура при резонансе носит резистивный характер: . При этом соблюдается равенство индуктивного сопротивления катушки и емкостного сопротивления конденсатора, то есть выполняется условие резонанса напряжений . Из выражения видно, что резонанс напряжений в контуре можно получить варьированием значений одного из параметров, а именно: частоты приложенного напряжения, индуктивностикатушки, или емкостиC конденсатора. Два других параметра при этом должны быть постоянными. В частности, при фиксированных значениях параметров ирезонанс в цепи наступит при резонансной частоте: . Рис. 1 Рис. 2 При резонансе ток в цепи принимает максимальное значение , если действующее значение напряжения на входе цепиU = const. При этом напряжения имогут быть много больше входного напряжения(отношениеможет достигать величин несколько сотен). Векторная диаграмма тока и напряжений для этого режима цепи приведена на рисунке 2. Из диаграммы видно, что реактивная составляющая напряжения на катушкеи напряжениена конденсаторе при резонансе в силу равенстваравны друг другу и сдвинуты по фазе на угол почти, если.. Вследствие падения напряжения в активном сопротивлении катушки, напряжение на катушкепри резонансе оказывается больше напряжения на конденсаторе, поэтому точка резонанса в этих условиях определяется по наибольшему значению тока в цепи. Частотная зависимость тока в цепи имеет вид: . Амплитудно- и фазочастотные характеристики тока можно записать в форме , . где – добротность контура, которая показывает во сколько раз напряженияина участках контура превышают приложенное напряжениеU; d – параметр затухания; – волновое (характеристическое) сопротивление резонансного контура. Частотные характеристики итакже какимеют максимум (рис. 3), причем максимумнаступает при частоте, а максимумпри частоте . Частоты и находятся из соотношений: , . Из соотношений видно, что с уменьшением сопротивления R (коэффициента затухания d) частоты истремятся к резонансной частотеи максимумы частотных характеристикисовмещаются. При возрастании сопротивленияR, наоборот, максимумы частотных характеристик расходятся. Анализ характеристики (рис. 4) показывает, что последовательный резонансный контур обладает частотной избирательностью или фильтрирующими свойствами. С небольшим ослаблением через контур можно передать сигналы(не более 3 Дб) в диапазоне частот. Указанную область частот называютполосой пропускания (прозрачности). Для контура формула относительной полосы пропускания частот имеет вид: . Активная мощность при резонансе имеет наибольшее значение, равное полной мощностиS, в то же время реактивная мощность цепи оказывается равной нулю. При этом реактивная индуктивная и реактивная емкостная составляющие полной мощности могут приобретать теоретически весьма большие значения, в зависимости от значений тока и реактивных сопротивлений. Описание лабораторного стенда и рабочее задание Собрать схему последовательного резонансного контура, используя съемную панель лабораторного стенда (рис. 5) и размещенные на ней тумблеры .Внимание! При сборке схемы с помощью тумблеров следует учитывать, что перевод тумблера в верхнее положение соответствует замыканию ключа на участке цепи. На съемной панели также размещены катушка индуктивности сопротивлением и индуктивностью, конденсатори резистор. Подключить схему последовательного резонансного контура к генератору низкой частоты (ГНЧ) через понижающий трансформатор (T). С помощью ГНЧ обеспечивается получение синусоидального входного напряжения, а также возможность с помощью ручек управления регулировки напряжения на выходе по амплитуде и частоте. Ручкой управления ГНЧ по уровню напряжения и показанию вольтметра PV1, подключенного к зажимам вторичной обмотки трансформатора, установить действующее значение напряжения в диапазоне В. Используя исходные данные пункта 1 рабочего задания рассчитать для резонансного контура: резонансную частоту ; волновое сопротивление ; добротность резонансного контура ; параметр затухания d; ток в контуре при резонансе при заданном напряжении; напряжение на катушке и напряжение на конденсаторе при резонансе В цепи (рис. 5), находящейся под напряжением, изменяя частоту ГНЧ с помощью ручек управления «Грубо» и «Точно» в окрестности расчетного значения , найти резонансную частотуопытным путем, так, чтобы на экране осциллографа угол сдвига фаз между напряжением на зажимах вторичной обмотки трансформатора(канал A) и напряжением (канал B) был близок нулю. В электрической цепи (рис. 5) измерить ток , входное напряжение на зажимах вторичной обмотки трансформатора, напряжение на катушкеи конденсаторес помощью вольтметраPV1, подключая его параллельно к участкам цепи, а также угол сдвига фаз между приложенным напряжением и напряжением на сопротивлении с помощью осциллографа , варьируя частоту ГНЧ (где = 0, 1, 2) от резонансной частоты через интервалы Гц с помощью ручек управления «Грубо» и «Точно». Результаты измерений занести в таблицу. Рис. 5 Дополнить таблицу пункта 4 рабочего задания расчетными данными, определив активную и реактивнуюсоставляющие напряжения на катушке индуктивности, реактивные сопротивления катушкии конденсатора, реактивное сопротивление цепиX, а также модуль полного сопротивления контура Таблица Тема 2. Исследование неразветленной цепи переменного тока. Резонанс напряжений. Нарисовать принципиальную электрическую схему для наблюдения резонанса тока
Резонанс токов: применение, принцип резонса тока, расчет контура
Что такое резонанс?
 Соединение двух ветвей при резонансе
Соединение двух ветвей при резонансеПрименение
Принцип резонанса токов
 Схема для питания конденсатора
Схема для питания конденсатора Схема: переключатель резонансной схемы
Схема: переключатель резонансной схемы Схема: ток в резонансной схеме равен нулю
Схема: ток в резонансной схеме равен нулюРасчет резонансного контура
Что такое резонанс токов
Содержание: Принцип действия резонансных токов
Практическое использование резонанса токов
Тема 2. Исследование неразветленной цепи переменного тока. Резонанс напряжений
Вопрос 1. Нарисовать схему замещения электрической цепи. Объяснить какие процессы отражают элементы этой схемы.
Вопрос 2. Записать выражение для полного сопротивления, тока и коэффициента мощности при резонансе напряжений.
Лабораторная работа № 3 резонанс напряжений
Краткие теоретические сведения
| Частота, Гц | Опыт | Расчет | |||||||||||
| , В | , В | , В | , В | , град | , мА | , В | , В | , Ом | , Ом | , Ом | , Ом | ||
7. По данным таблицы 1 пункта 5 рабочего задания построить графики зависимости ,,и.
8. По данным таблицы 1 пункта 5 рабочего задания построить графики зависимостей ,,и.
Вопросы к защите
Как практически можно определить состояние резонанса напряжений в последовательном резонансном контуре?
Как определить частоту собственных колебаний резонансного контура?
Почему в момент резонанса не равны напряжения на катушке индуктивности и конденсаторе?
В цепи последовательного резонансного контура заданы значения R и С. Определите индуктивность катушки , при которой в цепи возникнет резонанс, если ,. Определите, во сколько раз напряжение на емкости будет больше входного напряжения при резонансе.
Содержание отчета
Выполнение домашнего задания.
Электрическая схема испытаний резонанса напряжений. Определение резонансной частоты опытным и расчетным путем. Сопоставление данных расчета и эксперимента.
Построение графиков, характеризующих явление резонанса напряжений, по данным таблицы испытаний.
Определение добротности и волнового сопротивления резонансного контура.
Выводы.
studfiles.net
Лабораторная работа № 5 исследование разветвленной цепи синусоидального тока. Резонанс токов
Цель работы: исследование электрической цепи синусоидального тока при параллельном соединении индуктивной катушки и конденсатора. Научиться по опытным данным строить векторные диаграммы токов и напряжений, определять электрические параметры цепи. Понимать и уметь устанавливать резонанс токов в рассматриваемой цепи.
Краткая теория
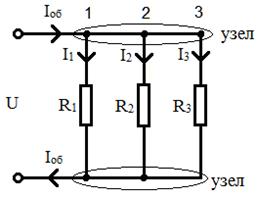
При параллельном соединении элементов (рисунок 1) уравнение по первому закону Кирхгофа для мгновенных значений и в комплексной форме имеет вид .
Рисунок 1
где ,;
В зависимости от соотношения реактивных проводимостей ивозможны три различных случая:
1. >, следовательно,>Этому режиму соответствует векторная диаграмма на рисунке 2а.
2. =, (=) - случай резонанса токов (рисунок 2б).
3. <, а значит<. Этот случай иллюстрирует векторная диаграмма на рисунке 2с.
Рисунок 2
Из условия резонанса токов =можно определить резонансную частоту. Для схемы (рисунок 1) имеем
.
При этом .
Рисунок 3
На рисунке 3 показаны резонансные кривые параллельного контура. При резонансной частоте токот источника имеет минимум и равен току на активном сопротивлении, а токна реактивном участке цепи равен нулю.
При цепь носит индуктивный характер (напряжение опережает ток на ток на угол), при- активный, а при- емкостной характер (ток опережает напряжение на угол).
Полное сопротивление при резонансе принимает максимальное значение, а реактивное сопротивлениеобращается в ноль.
При определении резонансной частоты в общем случае следует исходить из условия вещественности полной проводимости цепи - . Например, для цепи (рисунок 4) имеем
Рисунок 4
Поскольку в режиме резонанса мнимая часть должна быть равна нулю, то
.
Порядок выполнения работы
• Собрать схему исследования (рисунок 5).
Рисунок 5
•Подать синусоидальное напряжение от генератора напряжений специальной формы: .
• Измерить с помощью виртуальных приборов активное сопротивление катушки индуктивности и рассчитать теоретическую резонансную частоту -.
• Изменяя частоту приложенного напряжения, настроить резонансный режим по показанию фазометра или по минимуму тока. Сравнить экспериментальную резонансную частоту с расчетной.
• Снять резонансные кривые и фазочастотную характеристикупри переменной частоте входного сигнала.
• Результаты измерений занести в таблицу 1 и построить графики резонансных кривых.
• Снять частотные характеристики . Результаты измерений занести в таблицу 1 и построить графики частотныxхарактеристик.
Таблица 1
| Параметры | Значения параметров | ||||||||
| , Гц | 0,4 | 0,6 | 0,8 | 1,2 | 1,4 | 1,6 | 1,8 | 2 | |
| , А | |||||||||
| , А | |||||||||
| , А | |||||||||
| ,Ом | |||||||||
| ,Ом | |||||||||
• Построить векторные диаграммы напряжения и токов для трех значений частоты: ,и.
• Сделать выводы по работе.
Контрольные вопросы и задачи
1 Дайте определение резонанса токов.
2 В какой цепи и при каких условиях наступает резонанс токов?
3 Чем отличается резонанс токов от резонанса напряжения?
4 Изменяя какие параметры цепи, можно получить резонанс токов?
5 С помощью каких приборов и по какому признаку можно судить о возникновении резонанса токов?
6 Почему при резонансе токов ток в цепи минимален?
7 Оказалось, что при резонансе токов в цепи I1 = 10A,I2 = 5A,XС = 40 Ом. Определить величину индуктивного сопротивленияXL, Ом.
8 В параллельном колебательном контуре резонанс токов. Параметры цепи: R= 20 Ом;XL=40 Ом. Найти сопротивление конденсатора.
Лабораторная работа № 6
studfiles.net
Резонанс токов и его полезное применение в электротехнике :: SYL.ru
Резонансом в физике называют явление, при котором амплитуды колебания системы резко возрастают. Это происходит при совпадении собственной и внешней возмущающей частот. В механике примером может служить маятник часов. Подобное поведение характерно и для электрических схем, включающих в себя элементы активной, индуктивной и емкостной нагрузки. Резонанс токов и напряжений очень важен, это явление нашло применение в таких областях науки, как радиосвязь и промышленное электроснабжение.
Векторы и теория
Для понимания смысла процессов, происходящих в цепях, включающих катушки индуктивности, конденсаторы и активные сопротивления, следует рассмотреть схему простейшего колебательного контура. Подобно тому, как обычный маятник попеременно переводит энергию из потенциального в кинетическое состояние, электрический заряд в RCL-цепочке, накапливаясь в емкости, перетекает в индуктивность. После этого процесс происходит в обратном направлении, и все начинается сначала. При этом векторная диаграмма выглядит следующим образом: ток емкостной нагрузки опережает на угол π/2 направление напряжения, индуктивная нагрузка отстает на такой же угол, а активная совпадает по фазе. Результирующий вектор имеет наклон по отношению к абсциссе, обозначаемый греческой буквой φ. Резонанс в цепи переменного тока наступает тогда, когда φ=0, соответственно, cos φ = 1. В переводе с языка математики эта выкладка означает, что ток, проходящий по всем элементам, по фазе совпадает с током в активной составляющей электросхемы.
Практическое применение в системах электроснабжения
Теоретически все эти выкладки понятны, но что они значат для практических вопросов? Очень многое! Всем известно, что полезная работа в любой схеме выполняется активной составляющей мощности. При этом большая часть потребления энергии приходится на электродвигатели, которых на любом предприятии немало, а они содержат в своей конструкции обмотки, представляющие собой индуктивную нагрузку и создающие угол φ, отличный он нуля. Для того чтобы возник резонанс токов, необходимо скомпенсировать реактивные сопротивления таким образом, чтобы их векторная сумма стала нулевой. На практике это достигается включением конденсатора, который создает противоположный сдвиг вектора тока.
Резонанс токов в радиоприемных устройствах
Резонанс токов имеет и другое, радиотехническое применение. Колебательный контур, составляющий основу каждого приемного устройства, состоит из катушки индуктивности и конденсатора. Меняя величину электрической емкости, можно добиться того, что сигнал с требуемой несущей частотой будет приниматься избирательно, а остальные всеволновые составляющие, принимаемые на антенну, включая и помехи, окажутся подавленными. На практике такой переменный конденсатор выглядит как два набора пластин, один из которых при вращении входит или выходит из другого, увеличивая или уменьшая при этом электрическую емкость. При этом создается резонанс токов, а радиоприемник оказывается настроенным на нужную частоту.
www.syl.ru
Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.

Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.

С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.

Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту

Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

Выразим резонансную частоту
 Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
electroandi.ru










Поделиться с друзьями: