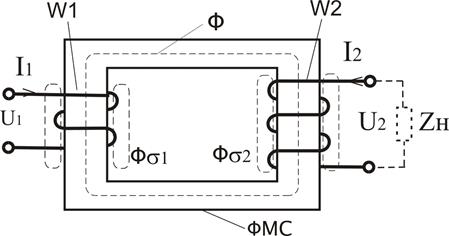
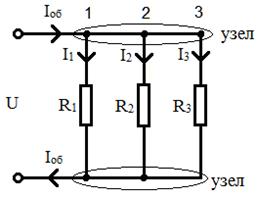
Соединение обмоток генератора звездой или треугольником позволяет уменьшить число проводов, соединяющих генератор с приемником, с шести при несвязанной системе до четырех или до трех. При соединении звездой (рис. 12.4) к началам обмоток генератора А, В, С присоединяют три линейных провода (желтый, зеленый, красный), идущих к приемнику. Концы обмоток X, У, Z объединяют в узел, называемый нейтралью генератора или его нейтральной точкой N. В четырехпроводной системе к нейтрали генератора присоединяется нейтральный провод (синий). В трехпроводной системе он отсутствует. Токи протекающие по линейным проводам называются линейными токами Iл. Так как в схеме соединения звездой линейный провод включен последовательно с фазой то линейный ток будет равен фазному. Напряжения между линейными и нейтральным проводами называются фазными напряжениями: uA, uB и uC. Фазное напряжение отличается от фазной ЭДС на падение напряжения в обмотке генератора. В дальнейшем будем считать, что падениями напряжения в фазах генератора можно пренебречь т.е. принять uA= eA, uB = eB и uC = eC или считать что заданы напряжения uA, uB и uC. Напряжения между линейными проводами называются линейными: uAB, uBC и uCA. Положительное направление напряжения указывается порядком записи индексов, например, положительное направление напряжения uAB от точки А к точке B (рис. 12.4). Мгновенные значения фазных напряжений равны разностям мгновенных значений потенциалов начала и концов соответствующих обмоток: uA= φA— φX, uB = φB — φY, uC = φC — φZ Мгновенные значения линейных напряжений равны разностям мгновенных значений потенциалов начал соответствующих обмоток, т.е. uAB= φA— φB, uBC = φB — φC, uCA = φC — φA (12.5) Концы обмоток соединены в узел, поэтому потенциалы их одинаковы φx= φy= φz. Мгновенное значение линейного напряжения между проводами A и B uBC = uB – uC; uCA = uC – uA. Следовательно, можно утверждать, что мгновенное значение любого линейного напряжения равно алгебраической разности мгновенных значений соответствующих фазных напряжений. Аналогично при символической записи любое комплексное линейное напряжение равно разности соответствующих фазных комплексных напряжений, т.е. На векторной диаграмме (рис. 12.5) изображены три вектора фазных напряжений Вектор любого линейного напряжения равен разности соответствующих векторов фазных напряжений. Из векторной диаграммы (рис. 12.5) видно, что векторы двух смежных фазных напряжений и вектор соответствующего линейного напряжения, например векторы или т.е. линейное напряжение в √З раз больше фазного напряжения. Кроме того, из рис. 12.5 следует, что звезда векторов линейных напряжений повернута на 30° в сторону вращения векторов относительно звезды векторов фазных напряжений. Алгебраическая сумма линейных напряжений всегда равна нулю. Действительно, приняв во внимание выражение 12.5 можно написать или У симметричной трехфазной системы равна нулю и сумма фазных напряжений: как и сумма фазных ЭДС (рис. 12.2) В этом можно убедиться, сложив соответствующие векторы, как это показано для фазных напряжений на рис. 12.5. Трехфазная система соединённая в звезду получила наибольшее распространение, так как в ней можно получить на нагрузке одновременно два напряжения линейное (√З * фазное, к примеру 220*√З = 380 в) и фазное (к примеру 220 в) . При этом нагрузка может быть как трехфазной так и однофазной, симметричной и не симметричной. electrikam.com В звезде с нейтральным проводом каждая фаза нагрузки с помощью нейтрального провода и соответствующей линии независимо подключена к своему генератору. Следовательно, если не учитывать малые падения напряжения в линии, фазные напряжения, также как ЭДС генератора равны по величине и сдвинуты по фазе на 1200. Соответственно, линейные напряжения Из векторной диаграммы линейных и фазных напряжений можно найти соотношение между ними. По теореме косинусов для любого линейного напряжения (учитывая, что cos1200 = – 0.5) получим Следовательно, в звезде с нейтральным проводом при любой нагрузке линейные напряжения (Uл) равны по величине и в Uл = UAB = UBC = UCA = Из схемы соединения нагрузки звездой следует, что линейные токи равны соответствующим фазным Ток в нейтральном проводе можно определить из I закона Кирхгофа для нейтральной точки нагрузки “n” Пример расчета трехфазной нагрузки, соединенной Звездой с нейтральным проводом Пусть известно линейное напряжение и сопротивления всех фаз 1. Определяем фазные напряжения Ua = Ub = Uc = Uл / 2. Определяем сопротивления фаз, фазные токи и углы сдвига фаз между током и напряжением Аналогично определяются Zb, Ib, φb; Zc, Ic, φc 3. Ток в нейтральном проводе определяется по векторной диаграмме (ВД) Порядок построения ВД 3.1. Строим 3 вектора фазных напряжений 3.2. Относительно каждого из этих напряжений строим фазные токи 3.3.Складываем геометрически фазные токи и находим ток в нейтральном проводе Трехфазное соединение нагрузки треугольником При соединении нагрузки треугольником каждая фаза нагрузки включена между двумя линейными проводами, следовательно, фазные напряжения равны соответствующим линейным Пример расчета трехфазной нагрузки, соединенной треугольником. 1. Определяем сопротивления фаз (Zab, Zbc, Zca) , фазные токи и углы сдвига фаз между током и напряжением Аналогично определяются Zbc, Ibc, φbc ; Zca, Ica, φca 2. Линейные токи можно определить по векторной диаграмме (ВД) на основания I закона Кирхгофа в векторной форме Для узла “a” Аналогично для узлов “b” и “c” получим Порядок построения ВД 2.1. Строим 3 вектора фазных напряжений 2.2. Относительно каждого из этих напряжений строим фазные токи 2.3. Строим вектор линейного тока – из фазного тока При обрыве одной из фаз ток в этой фазе равен 0, токи в двух оставшихся фазах и все фазные напряжения не изменяются. Линейные токи определяются по векторной диаграмме, как и в предыдущем случае. При обрыве линейного провода система перестает быть трехфазной. Схема представляет из себя две параллельные ветви, включенные между двумя оставшимися линейными проводами. Фазные и линейные токи можно определить на основе методов расчета цепи с параллельным соединением элементов.Тема 3 Трансформаторы Назначение –преобразование переменного тока одного напряжения в переменный ток другого напряжения без изменения частоты, т.е. для повышения или понижения напряжения. Без трансформаторов передача электроэнергии на большие расстояния была бы невозможна. Применение –очень широкое – вся силовая энергетика, практически все бытовые и промышленные электронные устройства и т.д. Устройство –две или более обмоток, расположенных на замкнутом ферромагнитном сердечнике (ФМС). Обмотка, которая подключается к сети, называется первичной.К остальным обмоткам (вторичным) подключаются нагрузки. Принцип действия трансформатораоснован на явлении электромагнитной индукции – законе Фарадея. При подключении первичной обмотки W1 к сети переменного тока с напряжением ~ U1 по ней течет переменный ток ~ I1, который будет создавать переменный магнитный поток Ф1. Основная часть этого потока Ф распространяется по ФМС (основной поток), пронизывает витки вторичной обмотки W2 и индуктирует в них ЭДС E2 (закон Фарадея). (при любом изменении магнитного потока в каждом витке индуктируется ЭДС, пропорциональная скорости изменения магнитного потока e ~ – dФ/dt. Если же ток постоянный, то Ф–const, => dФ/dt = 0, => e = 0, т.е. постоянный поток ЭДС не создает, => трансформатор не работает на постоянном токе). Если W2 > W1 то ЭДС вторичной обмотки Е2 > E1 => U2 > U1 – трансформатор повышающий. Если W2 < W1 то ЭДС вторичной обмотки Е2 < E1 => U2 < U1 – трансформатор понижающий. Назначение ФМС –ФМС служат для усиления магнитного поля и придания ему нужной конфигурации. При введении в катушку ФМС он намагничивается и его собственное магнитное поле складывается с полем катушки. В результате магнитный поток (МП) резко возрастает (приблизительно в m раз). m – магнитная проницаемость ФМС (до 10 000). Следовательно, используя ФМС, при том же токе в катушке можно получить в m раз больший МП, или заданный МП получить при в m раз меньшем токе в обмотке. Это огромный плюс использования ФМС.Но есть и минусы. ––В ФМС возникают дополнительные потери энергии (потери в стали) Рст = Рвт + Рг 1. Вихревые потери Рвт –ток переменный => МП переменный, он будет в самом ФМС индуктировать ЭДС (закон Фарадея), сердечник проводящий, по нему текут вихревые токи, которые разогревают сердечник. Для уменьшения этих потерь сердечники делают не сплошными, а набирают из тонких изолированных пластин, или прессуют из ферромагнитного порошка с диэлектрическим связующим. 2. Гистерезисные потери Рг –или потери на перемагничивание. Ток переменный, при каждом изменении направления тока ФМС перемагничивается, на это тратится энергия, пропорциональная частоте и площади петли гистерезиса. Для уменьшения этих потерь ФМС изготавливают из магнито-мягких материалов с узкой петлей гистерезиса. Потоки в трансформаторе Ф – основной поток – в ФМС Фs1 и Фs2 – потоки рассеяния каждой обмотки. Это часть потока, которая распространяется не по ФМС, а по воздуху. Но эти потоки малы, т.к. магнитное сопротивление воздуха в mФМС раз больше чем у ФМС (mвоздуха=1, а mФМС до 10000). Читайте также: lektsia.com Трехфазные электрические цепи получили широкое распространение в промышленности, благодаря своим немалым преимуществам перед другими системами электрических цепей. К ним относятся – экономичность передачи энергии, относительная простота создания вращающегося магнитного поля, а также возможность получения двух значений напряжения. Основными потребителями трехфазных систем являются асинхронные двигатели, а основными источниками – трехфазные генераторы. В разделе электротехники трехфазным цепям переменного тока посвящено немало задач, рассмотрим решение некоторых из них. Задача 1 Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю. а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом Линейные напряжения в данном случае будут равны и определяться как б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения. Линейные напряжения в данном примере будут разными по значению в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ. Как и в предыдущем примере, линейные напряжения не будут равны Задача 2 К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A1,A2 и фазные токи зная, что Uл=380В, R=50 Ом, xL=35 Ом. Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму) Напряжения в фазах будет равно Токи в фазах Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот) Соответственно, показания амперметров будут следующими: Задача 3 К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, xL=xC=10 Ом. Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа Сумма линейных токов Равенство нулю суммы линейных токов является свойством любой трёхфазной системы. Чтобы определить показания вольтметра, найдём сумму падений напряжения на xL и R в соответствующих обмотках. electroandi.ruСоединение обмоток генератора звездой. Линейные напряжения в трехфазной схеме звезда определяются как
Соединение обмоток генератора звездой | Электрикам
 Рисунок 12.4 Соединение обмоток генератора звездой
Рисунок 12.4 Соединение обмоток генератора звездой По аналогии для двух других линейных напряжений можем написать
По аналогии для двух других линейных напряжений можем написать Рис. 12.5 Векторная диаграмма фазных и линейных напряжений при соединении обмоток генератора звездой
Рис. 12.5 Векторная диаграмма фазных и линейных напряжений при соединении обмоток генератора звездой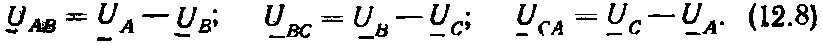

 образуют замкнутый треугольник. При симметричной системе напряжений действующие значения фазных напряжений равны друг другу, т.е. UA = UB = UC = UФ, и действующие значения линейных напряжений одинаковы, т.е. UAB = UBC = UCA = UЛ. Поэтому треугольник равнобедренный и имеет углы 30, 30 и 120 градусов. Из треугольника находим, что
образуют замкнутый треугольник. При симметричной системе напряжений действующие значения фазных напряжений равны друг другу, т.е. UA = UB = UC = UФ, и действующие значения линейных напряжений одинаковы, т.е. UAB = UBC = UCA = UЛ. Поэтому треугольник равнобедренный и имеет углы 30, 30 и 120 градусов. Из треугольника находим, что

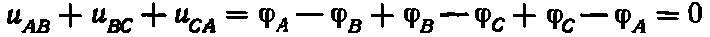



Трехфазное соединение звездой с нейтральным проводом
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒ 

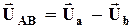
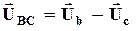

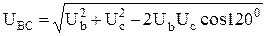 =
= 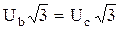
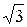 раз больше фазных (Uф).
раз больше фазных (Uф).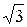 Uф =
Uф = 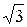 Ua =
Ua = 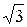 Ub =
Ub = 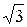 Uc
Uc
 – сумма геометрическая (векторная), следовательно, для определения In нужно построить векторную диаграмму.
– сумма геометрическая (векторная), следовательно, для определения In нужно построить векторную диаграмму. 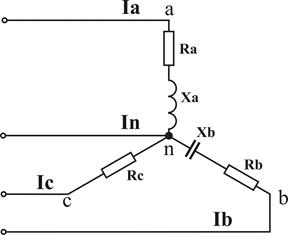
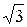
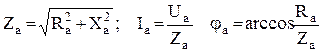
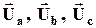 со сдвигом на 1200
со сдвигом на 1200 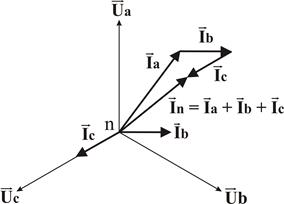
 , учитывая величину и направление угла сдвига фаз между током и напряжением.
, учитывая величину и направление угла сдвига фаз между током и напряжением.

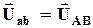
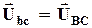
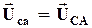

 =>
=> 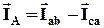
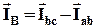 ;
;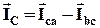
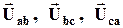 со сдвигом на 1200
со сдвигом на 1200 , учитывая величину и направление угла сдвига фаз между током и напряжением.
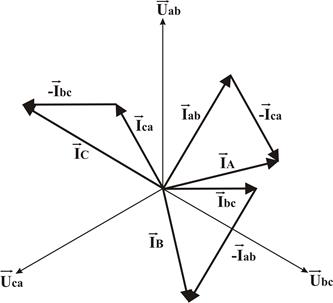
, учитывая величину и направление угла сдвига фаз между током и напряжением. по соотношению
по соотношению 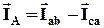
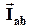 вычитаем фазный ток
вычитаем фазный ток 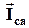 (т.е. из конца вектора
(т.е. из конца вектора 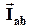 строим вектор минус
строим вектор минус 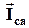 ) – получаем линейный ток
) – получаем линейный ток  . Аналогично находим линейные токи
. Аналогично находим линейные токи 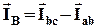 и
и 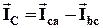 .
. 
Задачи на трехфазные цепи













 Фазное напряжение при данном соединении будет равно линейному, следовательно
Фазное напряжение при данном соединении будет равно линейному, следовательно  Фазные токи при несимметричной нагрузке не равны
Фазные токи при несимметричной нагрузке не равны 


 Так решаются задачи на трехфазные цепи. Спасибо за внимание! Читайте также - задачи на цепи переменный ток
Так решаются задачи на трехфазные цепи. Спасибо за внимание! Читайте также - задачи на цепи переменный ток
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''









Поделиться с друзьями: