Задачи Для схемы (рис. 5) найти токи в ветвях и напряжения между узлами а и b. R. Найти токи в ветвях схемы

Задачи Для схемы (рис. 5) найти токи в ветвях и напряжения между узлами а и b. R

Задачи

1. Для схемы (рис.5) найти токи в ветвях и напряжения между узлами а и b. R1= 1 кОм, R2= 2 кОм, R3= 3 кОм, R4 =4 кОм, Е1 =15 В, Е2 =35 В, Е3 =7 В, J1 =4 мА.

Решение. Выбираем произвольно положительное направление токов и напряжений в ветвях. Для решения воспользуемся законами Ома и Кирхгофа. Имеем в схеме два независимых узла и два контура.

По первому закону Кирхгофа для первого и второго узла получим

Рис.5

для первого узла,

для второго узла.

Выбираем направления обхода контуров и, пользуясь вторым законом Кирхгофа и законом Ома, составим еще два уравнения:

Подставим числовые значения, получим систему четырех уравнений с четырьмя неизвестными, которая имеет однозначное решение:

Решая систему уравнений, получим I1 =–5.57 мА, I2 =7.22 мА, I3 =1.65 мА, I4 =5.65 мА.

Воспользовавшись законом Ома и вторым законом Кирхгофа, найдем Uab:

2. Для схемы (рис.6) найти все токи, если Е1 =12 В, Е2 =19 В, R1 =4.7 кОм, R2 =8.2 кОм, R3 =2.2 кОм.

Рис.8

Рис.9

Рис.6

3. В неразветвленной цепи (рис.7) Е1 =12 В, Е2 =35 В, R1 =12 кОм, R2 =8.2 кОм. Определить напряжение между точками а и b.

4. В схеме моста (рис.8) известны сопротивления R1 =1.3 кОм, R2 =0.8 кОм, R3 =0.4 кОм. Сопротивление гальванометра RГ =0.6 кОм. Е =2.5 В, I1 =1 мА. Найти сопротивление R4.

5. В цепи (рис.9) найти Е1 и RХ, если Е2 =3 В, R1 =R2 =1 кОм, R3 =4 кОм, R4 =2 кОм, R5 =3 кОм. Амперметр А1 показывает 4 мА, а А2 – 3 мА; полярности приборов показаны на схеме, а их сопротивлениями можно пренебречь.

Рис.10

. Для цепи (рис.10) найти эквивалентные сопротивления между зажимами а и b, с , d и f, если R1 =6 кОм, R2 =5 кОм, R3 =15 кОм, R4 =30 кОм, R5 =6 кОм.

Решение. 1) расчет сопротивления Rab.

Эквивалентное сопротивление соединенных параллельно сопротивлений R4 и R5 найдем по формуле

кОм.

Оно соединено последовательно с R2. Их общее сопротивление R’ =R2+R45 =5+5= =10 кОм.

Сопротивление цепи состоит из сопротивления R1, последовательно с которым соединены два параллельных сопротивления R и R3:

кОм.

2) расчет сопротивления Rcd.

Сопротивления R4 и R5 соединены параллельно; сопротивление R3 включено последовательно с ними:

кОм.

Сопротивление Rcd состоит из двух параллельно включенных сопротивлений R2 и R и равно

кОм.

3) расчет сопротивления Rdf.

Эквивалентное сопротивление цепи между точками d и f состоит из трех параллельно включенных сопротивлений R5, R4 и R2+R3 и может быть определено из формулы:

откуда Rdf. = 4 кОм.

7. Определить эквивалентное сопротивление цепи между точками а и b при разомкнутом и замкнутом ключе К (рис.11). Дано: R1=R2=R3=R4=R5=R6=R7=10 кОм.

Рис.12

Рис.11

Рис.13

8. Определить токи в ветвях цепи (рис.12) и показание вольтметра, включенного между точками c и d , считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи. Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю? Сопротивления элементов цепи: R1 =2.7 кОм, R2 =R3 =R5 =2.5 кОм, R4 =5.6 В, Е =70 В.

9. В схеме (рис.13) найти сопротивление Rx, если I1 =2.6 мА, I3 =0.6 мА, R1 =0.5 кОм, R2 =1.4 кОм, R3 =3 кОм, R4 =2.5 кОм; найти Е, если внутреннее сопротивление источника напряжения Ri равно 100 Ом.

10. Для цепей (рис.14,а,б) определить относительное напряжение на выходе U2 (выходные зажимы цепи разомкнуты) к напряжению U1 на входе цепи. Сопротивления отдельных ветвей цепи в килоомах указаны на схемах.

б)

Рис.17

1. При заданных значениях R1=4.3 кОм, R2=7.5 кОм, R3=5.1 кОм, R4 =6.8 кОм, R =0…47 кОм, Е =9 В (рис.17) вычислить ток I2 при максимальном R. Вычислить I0. Найти величину R, при котором I2=0. На сколько изменится при этом I0?

Решение. Используя законы Кирхгофа, составляем систему уравнений, в которой переменными являются токи. Выразим все токи через I1, I2, I3:



Решая систему методом Крамера, получаем =7976.941, 2=1894.14, 3=6771.06; I2=2/=0.237 мА, I3=0.849 мА, I0=1.086 мА.

Ток I2 равен нулю только в том случае, если напряжение на R2 равно нулю. Тогда R2= можно исключить из схемы. Получаем , , значит

, 5.73 (кОм).

При этом I0 = E/(R1 + R3) = 0.957 мА.

Изменение I0 равно I0 = 0.957-1.086 = –0.129 мА.

12. Для измерения силы тока в линейной цепи были использованы разные милли-амперметры и шунт. Известно, что внутреннее сопротивление первого милли-амперметра R1=115 Ом, второго R2=47 Ом, сопротивление шунта Rш=159 Ом. При подключении шунта к первому прибору его ток полного отклонения стал Iп1=10 мА, ко второму – Iп2=20 мА. При подключении в цепь первый прибор показал I1=3.7 мА, второй – I2=4.1 мА. Определить эквивалентное сопротивление цепи Ri и ток в цепи до подключения приборов.

Решение. Вычислим сопротивления приборов с подключенными шунтами. Сопротивление первого миллиамперметра равно

Ом,

второго

Ом.

Составим схему (рис.18). Токи I1 и I2 равны, соответственно:

Рис.18

Отсюда ,

Ом.

Но до подключения приборов в цепи протекал ток , , величиной , который определим, вычислив Е,

Получим

мА.

13. Найти коэффициент передачи по напряжению цепи (рис.19), если R1=R2 =R4= R7=2.2 кОм, R3= R5= R6= R8 =4.7 кОм.

Рис.19

Рис.20

Рис.21

Подсказка. Сначала упростим схему, приведя её к виду (рис.20), заменив цепь, состоящую из R4… R8 на Rэ.

14. Определить параметры генератора тока, эквивалентного цепи, показанной на рис.21. Параметры: R1… R6=6.2 кОм, E1=E2=10 В, I1= I2=1.5 мА.

Подсказка. Сначала преобразуем источники напряжения в эквивалентные источники тока.

Ответ: Uх.х.=6.783 В,

Рис.22

Jк.з.=0.938 мА.

15. Найти напряжение UR7 (рис.22) при данных значениях сопротивлений: R1=R2=R3=2.2 кОм,

R4=R5 =R6=R7=4.3 кОм. E=6.3 В.

Ответ: =2.089 В.

Подсказка. Сначала преобразуем «звезды» R1– R2– R3 и R4–R5–R6 в «треугольники».

16. Методом контурных токов найти токи в цепи (рис.23). Дано: E1=100 В, E2=60 В, E3=12 В, E4=7 В, R1=R2=10 кОм, R3=6 кОм, R4=4.7 кОм, R5=15 кОм.

Рис.23

Рис.24

17. Найти все токи в схеме (рис.24), а также отношение U3 к I4, если E1=12 В, E2=27 В, E3=5 В, J1=19 мА, R1=5.6 кОм, R2=3.3 кОм, R3=6.8 кОм, R4=2.7 кОм, R5=18.7 кОм, R6=8.2 кОм, R7=4.7 кОм.

Решение. Преобразуем источник тока с параллельно включенным сопротивлением в источник напряжения с последовательно включенным сопротивлением

, В.

Составим матрицы [U], [R] и [J]

JI=–2.69 мА, JII=–3.09 мА, JIII=–2.71 мА,

I1=2.69 мА, I2=3.09 мА, I3=0.40 мА,

I4=–22.09 мА, I5=–0.02 мА, I6=–0.38 мА, I7=–2.71 мА, кОм.

Рис.25

Рис.26

18. Для схемы (рис.25) вычислить токи. Заданы токи и внутренние проводимости генераторов тока первого и второго, соответственно: J1=50 мА, g1=10-4 Сим, J2=60 мА, g2=510-4 Сим. E3=270 В, R3=1 кОм, R4=2 кОм, R5=7.5 кОм, R6=3 кОм. Задачу решить методом контурных токов.

19. Для схемы (рис.26) составить матрицу сопротивлений и найти схемные функции I4/J1, U3/E1, U3/J1, I4/U2. Дано: J=20 мА, E1=11 В, E2=17 В, E3=23 В, R1=1 кОм, R2=3 кОм, R3=4.3 кОм, R4=13 кОм, R5=8.2 кОм, R6=5.6 кОм,.

20. Для схемы (рис.27) составить матрицу сопротивлений и найти схемные функции E1/U5, J2/U5, U7/U3, U5/J1. Найти также токи в каждой ветви. Параметры элементов схемы: R1=R3=R5=R7=R9=4.7 кОм, R2=R4=R6=R8=7.5 кОм,. J1=10 мА, J2=35 мА, J3=7 мА, E1=E2=E3=E4=E5=27 В.

Рис.27

Рис.28

21. Для схемы (рис.28) составить матрицу сопротивлений, вписав в неё зависимые источники напряжения. Найти схемную функцию U2/U1, если r1=3 В/мА, r2=5 В/мА, r3=8 В/мА, R1=R3=R5=4.3 кОм, R2=R4=12 кОм.

Решение. Введем обозначения:

Составим согласно МКТ систему уравнений

Поскольку напряжения зависимых источников напряжения матрицу сопротивлений E1, E2, E3 зависят от величины неизвестных контурных токов, то множители при этих токах r1, r2, r3 необходимо из столбца напряжений перенести в матрицу сопротивлений с противоположными знаками. При этом матрица сопротивлений будет иметь вид:

Теперь найдем схемную функцию U2/U1:

22. Для схемы (рис.29) составить матрицу сопротивлений, вписав в неё все зависимые источники. Найти следующие схемные функции U3/I5, I5/U3., U5/U1, если 1=6, r1=2 В/мА, r2=7 В/мА, r3=4.5 В/мА, R1=7.5 кОм, R2=12 кОм, R3=1.2 кОм, R4=4.7 кОм, R5=18 кОм.

23. Для схемы (рис.30) составить матрицу сопротивлений, вписав в неё все зависимые источники. Найти схемные функции U2/U1, I3/U1U1/I3, U2/I3, I3/U2, если r=11 В/мА, S1=7 мА/В, S2=19 мА/В R1=R2=R3=6.8 кОм, R4=R5=7.5 кОм, R6=12 кОм.

24. Для схемы (рис.31) составить матрицу сопротивлений, вписав в неё все зависи-мые источники. Найти схемную функцию U2/U1. Параметры схемы r1=12 В/мА, r2=3 В/мА, S=16 мА/В, R1=R2=3.3 кОм, R3=1.2 кОм, R4=0.5 кОм, R5=R6=8.2 кОм.

Рис.29

Рис.30

Рис.31

gigabaza.ru

Расчет токов в схеме с одним источником энергии

При расчете токов в электрических цепях с одним источником электрической энергии рассматривают два типа задач: прямуюзадачу иобратную.

Прямая задача. Определить неизвестные токи и напряжение на зажимах источника ЭДС в электрической цепи, схема которой приведена на рис. 1.9, если известен ток четвертой ветвиI4.

Решение этой задачи выполняется с помощью законов Ома и Кирхгофа.

Четвертая и пятая ветви соединены параллельно, то есть напряжение на зажимах этих ветвей одно и то же. По закону Ома определим это напряжение, зная ток и сопротивление четвертой ветви:.

Тогда ток пятой ветви:

Ток третьей ветви найдем по первому закону Кирхгофа:

откуда.

Для определения тока второй ветви составим уравнение по второму закону Кирхгофа для контура, образованного второй, третьей и четвертой ветвями:

из составленного уравнения найдем ток второй ветви

Ток первой ветви находим, составив уравнение по первому закону Кирхгофа для узла 2:

откуда

ЭДС источника рассчитаем, составив уравнение по второму закону Кирхгофа для контура, образованного первой и второй ветвями:

Обратная задача. Определить токи в ветвях электрической цепи, схема которой показана на рис. 1.9, если известны сопротивления приемников и ЭДС источника питания.

Цепь содержит один источник ЭДС. Токи в такой цепи направлены от точки с самым высоким потенциалом (1) через приемники к точке с самым низким потенциалом (5), и можно сразу показать правильные положительные направления токов ветвей.

Задачу решаем методом эквивалентных преобразований.

Путем последовательных преобразований необходимо определить входное сопротивление цепи относительно зажимов источника, то есть привести схему к виду рис. 1.10.

В такой цепи, содержащей источник и приемник электрической энергии, напряжение на зажимах приемника равно ЭДС и ток, протекающий по цепи, может быть определен с помощью закона Ома:

Рассчитаем входное сопротивление цепи относительно зажимов 1-5.

Найдем сопротивление пятой ветви, содержащей последовательное соединение сопротивлений R5иR6:

Пятая и четвертая ветви соединены параллельно, поэтому их эквивалентное сопротивление, найденное относительно зажимов 3-4,равно:

Сопротивление третьей ветви и найденное сопротивление R45соединены последовательно, их эквивалентное сопротивление:

Относительно зажимов 2-4 сопротивления второй ветви и сопротивление R345соединены параллельно:

Относительно зажимов источника ЭДС сопротивление R2345и сопротивление первой ветви соединены последовательно, поэтому входное сопротивление можно рассчитать:

Ток ветви, содержащей источник ЭДС, определим по закону Ома:

Ток второй ветви определим из уравнения, составленного по второму закону Кирхгофа для контура, образованного первой и второй ветвями:

, откуда

Ток третьей ветви найдем с помощью уравнения, составленного по первому закону Кирхгофа для узла 2:

откуда

Для определения тока четвертой ветви составим уравнение по второму закону Кирхгофа для контура, образованного второй, третьей и четвертой ветвями:

откуда

Ток пятой ветви найдем с помощью уравнения, составленного по первому закону Кирхгофа для узла 3:

откуда

studfiles.net

Примеры решения задач

1. Расчет цепей постоянного тока

Пример 1

Рассчитать токи в ветвях схемы показанной на рис. 2.1. Если Е1=100В, R1=100 Ом, R2=100 Ом, R3=60 Ом, R4=40 Ом, R5=56 Ом, R6=20 Ом.

Рис. 2.1. Схема электрической цепи к примеру 1

ешение:

Так как электрическая цепь содержит один источник электрической энергии, то расчет целесообразно вести методом эквивалентных преобразований. Перед началом расчета необходимо расставить направление токов, определить количество узлов и ветвей. Направление токов на схеме соответствует направлению ЭДС источника (см. рис. 2.1), схема содержит пять ветвей и три узла (a, b, c). В схеме на рис. 2.1 сопротивления R3 и R4 соединены параллельно, их эквивалентное сопротивление равно:

Сопротивления R34, R5 и R6 соединены последовательно, их эквивалентное сопротивление равно:

Сопротивление R2 и сопротивление R3456 соединены параллельно, следовательно:

Сопротивление R1 соединено последовательно с R23456 следовательно, эквивалентное сопротивление всей схемы равно:

Ток, потребляемый от источника ЭДС:

Чтобы рассчитать остальные токи схемы необходимо определить напряжение между узлами a и b:

Зная напряжение можно определить токи:

Чтобы рассчитать токи, протекающие по сопротивлениям R3 и R4 необходимо определить напряжение на участкеac:

Зная это напряжение, определим токи:

Выполняем проверку правильности решения с помощью первого закона Кирхгофа для узлов aи с:

I1 -I2 -I3 -I4 = 1А – 0.5А – 0.2А – 0.3А = 0,

I3 +I4 –I5 = 0.2А + 0.3А – 0.5А = 0.

Так как законы Кирхгофа выполняются, то расчет выполнен правильно.

Пример 2

Рассчитать токи в ветвях схемы показанной на рис. 2.2. Если Е1=100В, Е2=75В, Е3=50В R1=100 Ом, R2=50 Ом, R3=20 Ом, R4=40 Ом, R5=40 Ом.

Решение:

Рис. 2.2. Схема к примеру 2

еред началом расчета необходимо расставить направление токов, определить количество узлов и ветвей. Так как в схеме несколько источников ЭДС используем условно-положительные направления токов. На схеме направление токов соответствует направлению ЭДС в активных ветвях, а в пассивной ветви выбрано произвольно (см. рис. 2.2), схема содержит четыре ветви и два узла (a, b). Так как в схеме два узла и несколько источников ЭДС, то расчет целесообразно вести методом двух узлов. Обозначим направление межузлового напряжения. Рассчитаем проводимости ветвей:

В соответствии с методом двух узлов межузловое напряжение будет равно:

Зная межузловое напряжение, определяем токи в ветвях, используя второй закон Кирхгофа:

Выполняем проверку правильности решения с помощью первого закона Кирхгофа для узла a:

I1 +I2 -I3 -I4 = 0.826А + 1.151А – 0.291А – 1.686А = 0,

Так как законы Кирхгофа выполняются, то расчет выполнен правильно.

Пример 3

Решить задачу, приведенную в примере 2 с помощью метода наложения.

Рис. 2.3. Схемы к примеру 3

ешение:

Так как схема на рис. 2.2 содержит три источника ЭДС, то расчет одной сложной цепи сводится к расчету трех простых цепей, показанных на рис. 2.3. Направления токов в исходной схеме показаны на Рис. 1.5, в схемах на рис. 2.3 направления токов обозначены в соответствии с направлением источников ЭДС. Рассчитаем первую схему (рис. 2.3, а). Сопротивления R2, R34 и R5 соединены параллельно, их эквивалентное сопротивление равно: .

Сопротивления R1 и R23456 соединены последовательно, следовательно эквивалентное сопротивление первой схемы:

Ток, потребляемый от источника Е1, равен:

Чтобы определить токи в оставшихся ветвях необходимо найти напряжение: .

Токи в ветвях:

Рассчитаем вторую схему (рис. 2.3, б). Сопротивления R1, R34 и R5 соединены параллельно, их эквивалентное сопротивление равно:

Сопротивления R2 и R13456 соединены последовательно, следовательно эквивалентное сопротивление первой схемы:

Ток, потребляемый от источника Е2, равен:

Чтобы определить токи в оставшихся ветвях необходимо найти напряжение: .

Токи в ветвях:

Рассчитаем третью схему (рис. 2.3, в). Сопротивления R1, R34 и R2 соединены параллельно, их эквивалентное сопротивление равно:

Сопротивления R5 и R1234 соединены последовательно, следовательно эквивалентное сопротивление первой схемы:

Ток, потребляемый от источника Е3, равен:

Чтобы определить токи в оставшихся ветвях необходимо найти напряжение: .

Токи в ветвях:

В качестве положительных направлений токов принимаем их направления на исходной схеме (рис. 2.2). С учетом этого токи схемы на рис. 2.2 определятся как:

studfiles.net

electroteck

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

РАСЧЕТНОЕ ЗАДАНИЕ № 1

по курсу «Электротехника и электроника»

РАСЧЕТ ЦЕПИ ПОСТОЯННОГО ТОКА

вариант 16

Исполнитель:

студент Лукашина Н.В.

группа С-31

Москва 2002

ЗАДАНИЕ

Для схемы 1:

Написать по законам Кирхгофа систему уравнений для определения неизвестных токов и ЭДС в ветвях схемы (решать эту систему уравнений не следует).
Определить неизвестные токи и ЭДС в ветвях схемы методом контурных токов.
Составить баланс мощностей для исходной схемы.
Определить напряжения, измеряемые вольтметрами.
Методом эквивалентного генератора определить ток во второй ветви (E2,R2), а также найти величину и направление ЭДС, которую надо дополнительно включать в эту же ветвь, чтобы тое в ней увеличился в 2 раза и изменил свое направление. Примечание: ЭДС эквивалентного источника напряжения определить из расчета режима холостого хода второй ветви; расчет токораспределения в оставшейся части схемы выполнить методом узловых потенциалов; входное сопротивление эквивалентного источника определить методом преобразования схемы.
Выполнить моделирование в программе ElectronicWorkBench5.0.

Параметры схемы приведены в таблице 1.

(Ом)

(В)

(А)

Выберем направление ЭДС Е1совпадающим с направлением токаI1. На схеме 2 пронумерованы узлы (1-5), обозначены выбранные направления токовI2,I3,I4,I5,I6,I8(I1,J– заданы) в ветвях и контурных токовI11,I22,I33,I44, а также направление обхода контуров (по часовой стрелке).

ЗАДАНИЕ 1

Написать по законам Кирхгофа систему уравнений для определения неизвестных токов и ЭДС в ветвях схемы (решать эту систему уравнений не следует).

m= 7 ветвей (6 неизвестных токов и 1 неизвестная ЭДС)
n= 5 узлов
Составляем (n-1) = 4 уравнения по первому закону Кирхгофа: узел 1:I2 +I1=I8узел 2:I8=I6 +Jузел 3:J+I6=I4 +I3узел 4:I4 +I5=I2

Составляем (m-(n-1)) = 3 уравнения по второму закону Кирхгофа: контур 1: -E2 -E5 +E1= -I2R2 -I5R5 +I1R1контур 2: -E4 +E3 +E5=I3R3 +I5R5 контур 3: -E1 -E3 +E6= -I1R1 -I3R3 -I6R6 -I8R8

ЗАДАНИЕ 2

Определить неизвестные токи и ЭДС в ветвях схемы методом контурных токов.

Контурный ток I44нам известен:I44 = -J. Следовательно, достаточно составить 3 уравнения .

контур 1: - E4 + E3 + E5 = I11(R3 + R5) – I22R5 – I33R3 (2.1)

контур 2: - E2 – E5 + E1 = I22(R2 + R5 + R1) – I11R5 – I33R1 (2.2)

контур 3: - E1 – E3 + E6 = I33(R1 + R3 + R6 + R8) – I22R1 – I11R3 – I44R6 (2.3)

Токи в ветвях:

I1=I22–I33(токI1= 2 А по условию)(2.4)

I2 = - I22

I3 = I11 – I33

I4 = - I11

I5 = I11 – I22

I6 = I44 - I33 = - J - I33

I8 = - I33

Решаем систему уравнений (2.1)-(2.4) относительно I11,I22,I33,E1.

С помощью MathCad2000PROполучены следующие результаты:

I11 = - 1,8 A

I22 = - 5 A

I33 = - 7 A

E1 = 71,8 B

Таким образом, получены следующие значения токов в ветвях схемы:

I2 = 5 A

I3 = 5,2 A

I4 = 1,8 A

I5 = 3,2 A

I6 = 2 A

I8 = 7 A

ЗАДАНИЕ 3

Составить баланс мощностей для исходной схемы.

 I2R = I12R1 + I22R2 + I32R3 + I52R5 + I62R6 + I82R8 = 501,6 Вт

 EI = E1I1 + E2I2 + E3I3 + E4I4 + E5I5 –E6I6 = 721,6 Вт

 UjJ = UjJ

Uj=3-2(см. схему 2)

2 = 3 + I6R6 + E6



Uj = - I6R6 - E6



 UjJ = J(- I6R6 - E6) = -220 Вт

S I2R = S EI + S UjJ

501,6 Вт = 721,6 Вт – 220 Вт - верно

ЗАДАНИЕ 4

Определить напряжения, измеряемые вольтметрами.

По условию потенциал узла 5 принимается равным нулю. Тогда: 5 = 0 U1 = 4 - 5 = 4 = E5 – I5R5 = 30,8 B
U2 = 3 - 6 3 = 6 – E1 – E3 + I3R3  U2 = – E1 – E3 + I3R3 = -81,0 B

ЗАДАНИЕ 5

Методом эквивалентного генератора определить ток во второй ветви (E2, R2), а также найти величину и направление ЭДС, которую надо дополнительно включать в эту же ветвь, чтобы тое в ней увеличился в 2 раза и изменил свое направление. Примечание: ЭДС эквивалентного источника напряжения определить из расчета режима холостого хода второй ветви; расчет токораспределения в оставшейся части схемы выполнить методом узловых потенциалов; входное сопротивление эквивалентного источника определить методом преобразования схемы.

Схема 3

За направление Еэкввзяли направление Е2.

Расчет Rэквотносительно точек А и В по схеме 4 (источники ЭДС закорочены, источники тока оборваны,R2в расчет на принимается).

Схема 4

R135 = R1 + R35 = 10,4 Ом

R68 = R6 + R8 = 10 Ом

Расчет Еэквс помощью метода узловых потенциалов по схеме 5.

Узел 1 – базовый: j1= 0.

По первому закону Кирхгофа:

для узла 3: J + I5 - I6 - I3 = 0 (5.1)

для узла 2: I3 – I5 – I18 = 0 (5.2)

Согласно закону Ома:

I5 = (2 - 3 + E5 – E4)G5 (5.3)

I6 = (3 - 1 + E6)G6 (5.4)

I3 = (3 - 2 + E3)G3 (5.5)

I18 = (2 - 1 + E1)G18 (5.6)

Подставляем (5.3)-(5.6) в (5.1) и (5.2) и получаем:

j2(G5+G3) +j3( -G5–G6–G3) =E4G5+E6G6+E3G3–E5G5–J(5.7)

j2( - G3 – G5 – G18) + j3(G5 + G3) = E5G5 – E3G3 – E4G5 + E1G18 (5.8)

Результат решения системы уравнений (5.7)-(5.8), полученный в MathCad2000PRO:

j2 = - 22,839 B

j3 = - 26,157 B

Потенциалы точек А и В относительно базисного узла:

jВ=j3+E4

jА=I18R8–E2Eэкв=jВ-jА=j3+E4-I18R8+E2= = 50,490 В

Расчет тока I2.
Нахождение величины и направления ЭДС, которую надо дополнительно включить в ветвь 2, чтобы ток в ней увеличился в 2 раза и изменил свое направление. (за направление Едопвзяли направление Еэкв)Величина дополнительной ЭДС: 151,47 В Направление дополнительной ЭДС: противоположно Е2

ЗАДАНИЕ 6

Выполнить моделирование в программе Electronic WorkBench 5.0.

Результаты моделирования исходной схемы и расчета величин токов и напряжений в программе ElectronicWorkBench5.0 приводятся далее.

studfiles.net

Расчет простых цепей при постоянных токах и напряжениях. Расчет сложных цепей с помощью прямого применения законов Кирхгофа (главы 1-2 учебного пособия "Теоретические основы электротехники в примерах и задачах"), страница 2

Окончательно для токов , 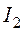получим (рис. 1.8)

;

5. Ток определим из уравнения, составленного по первому закону Кирхгофа для узла 1 (рис.1.6)

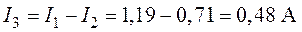6. Из уравнений, составленных по первому закону Кирхгофа, для узлов 3 и 2 (рис. 1.6) определим токи и :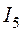

;

Задача 1.3.

Определить показание амперметра, установленного в ветви с источником ЭДС (рис. 1.12), если , , , , , , 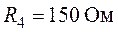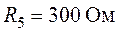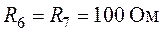. Внутренним сопротивлением амперметра можно пренебречь ().

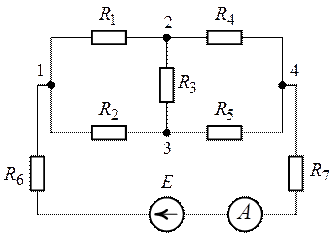
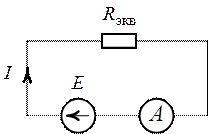
Рис. 1.12. Рис. 1.13.

Решение.

1. Методом свертывания цепи преобразуем схему рис. 1.12 к виду, приведенному на рис. 1.13.

Заменим треугольник сопротивлений, подключенный к точкам 1, 2 и 3 (рис. 1.12), эквивалентной звездой с вершинами 1, 2 и 3 (рис. 1.14).

Величины сопротивлений эквивалентной звезды:

;

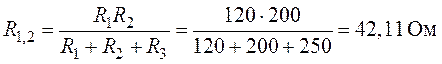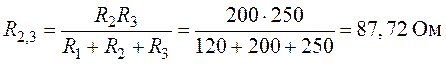Рис. 1.14. Рис. 1.15.

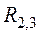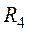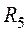Сопротивление соединено последовательно с , а сопротивление последовательно с (рис. 1.14). Участок цепи с сопротивлениям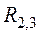и и 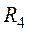включен параллельно участку с сопротивлениями и 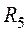(рис. 1.14).

Общее сопротивление обоих участков схемы (рис. 1.15) равно:

Сопротивления , , , 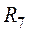(рис. 1.15) включены последовательно. Эквивалентное сопротивление всей цепи (рис. 1.13)

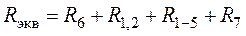
2. Показание амперметра соответствует току (рис. 1.13):

Задача 1.4.

Определить величину источника тока, установленного на входе цепи (рис. 1.16), если показание амперметра в разветвленной части схемы составляет 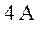. Сопротивления резисторов 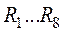равны .

Внутреннее сопротивление источника . Внутренним сопротивлением амперметра можно пренебречь ().

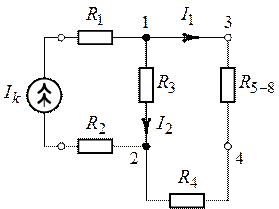
Рис. 1.16. Рис. 1.17.

Решение.

1. Пользуясь методом свертывания, приведем участок цепи (рис. 1.16) относительно узлов 3 и 4 к виду, представленному на рис. 1.17.

Общее сопротивление участка цепи

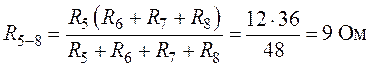2. Напряжение между узлами 1 и 2 (рис. 1.17)

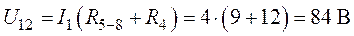3. Ток 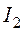в ветви с сопротивлением 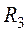(рис. 1.17)

4. Ток источника на входе цепи определим на основании первого закона Кирхгофа:

Задача 1.5.

В схеме (рис. 1.18) найти токи, применив метод пропорционального пересчета, если , , , , , .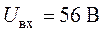

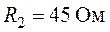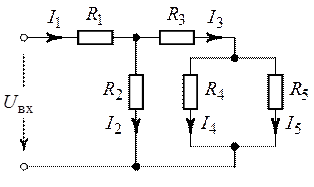
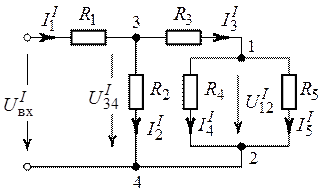
Рис. 1.18. Рис. 1.19.

Решение.

1. В рассматриваемой цепи зададим ток в одной из удаленных от источника ветвей, например, с сопротивлением 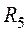, равным и определим некоторое напряжение источника на входе цепи 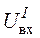, при котором 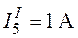(рис. 1.19)

2. Определим токи 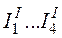(рис. 1.19)

Напряжение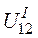

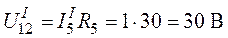Ток 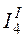равен: .

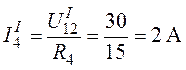Ток 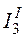определим как сумму токов и

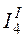
Напряжение на сопротивлении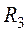

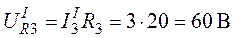Напряжение между узловыми точками 3 и 4

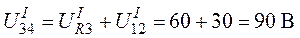Ток определим как

Ток на входе цепи определим как сумму токов и :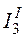

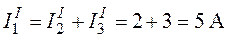Напряжение на сопротивлении

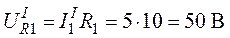Напряжение на входе цепи

3. Определим коэффициент пересчета как отношение напряжения на входе цепи, заданного по условию задачи , к найденному при расчетах :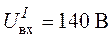

4. Действительные токи в ветвях цепи найдем как

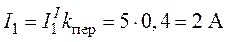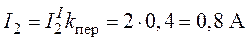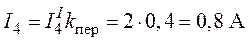Задачи для самостоятельного решения

Задача 1.6. Определить эквивалентное сопротивление электрической цепи, представленной на рис. 1.20, относительно зажимов 1 и 2, в которой сопротивления равны .

О т в е т: .

Рис. 1.20. Рис. 1.21.

Задача 1.7. Определить эквивалентное сопротивление цепи (рис.1.21) между входными зажимами 1 и 2 при разомкнутом и замкнутом положениях ключа (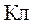), если , , , , , .

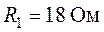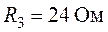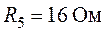О т в е т: при разомкнутом ключе 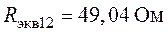; при замкнутом ключе .

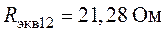Задача 1.8. Определить токи в ветвях цепи (рис. 1.22), если задано , , , , , .

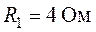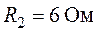О т в е т: , , , ,

, .

Задача 1.9. В схеме (рис. 1.23) определить токи во всех ветвях, если , , , , , .

О т в е т: , , , ,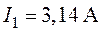

, .

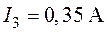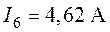Рис. 1.22. Рис. 1.23.

Задача 1.10. Определить токи во всех ветвях схемы (рис. 1.24), если задано , , , .

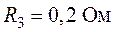О т в е т: , , , ,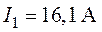

, .

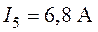Задача 1.11. В электрической схеме рис. 1.25 определить токи во всех ветвях, если задано , , , , .

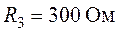О т в е т: , , , , , .

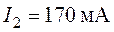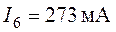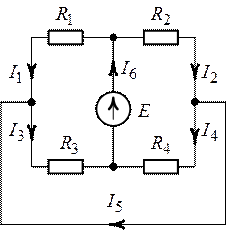
Рис. 1.24. Рис. 1.25.

Задача 1.12. Определить показание амперметра для схемы рис. 1.26, если , , , , . Принять .

О т в е т: .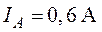

Задача 1.13. Определить показание амперметра для схемы рис. 1.27, если , , 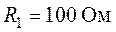, , 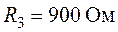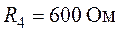. Принять .

О т в е т: .

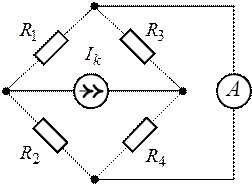
Рис. 1.26. Рис. 1.27.

Задача 1.10. Показание амперметра (рис. 1.28), установленного в разветвленной части схемы, составляет . Найти величину источника тока , если , , , . Сопротивление источника считать , амперметра .

О т в е т: .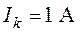

Задача 1.11. Найти все токи в ветвях цепи, схема которой приведена на рис. 1.29, если 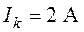, , , , 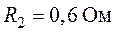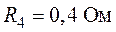. Принять сопротивление источника .

О т в е т: , , , ,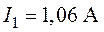

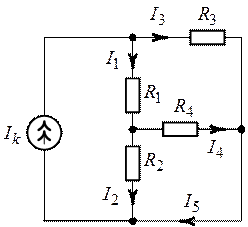
Рис. 1.28. Рис. 1.29.

Задача 1.12. Определить показание амперметра в схеме (рис. 1.30), если , , 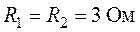, , 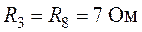. Принять .

О т в е т: .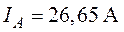

Задача 1.13. Методом пропорционального пересчета найти все токи в схеме рис. 1.31, если 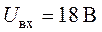, , , , 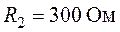, , , 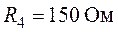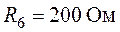. В расчетах принять ток в сопротивлении равным .

О т в е т: , , , , , , .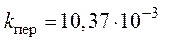

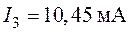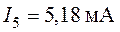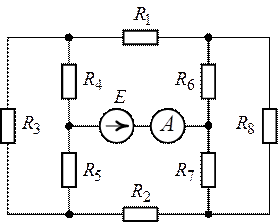
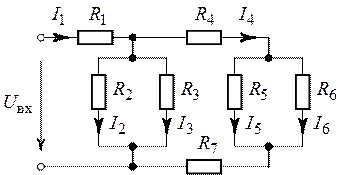
Рис. 1.30. Рис. 1.31.

2. РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ С ПОМОЩЬЮ ПРЯМОГО ПРИМЕНЕНИЯ ЗАКОНОВ КИРХГОФА

Законы Кирхгофа лежат в основе расчета сложных цепей содержащих несколько источников энергии. С помощью двух законов Кирхгофа устанавливаются соотношения между токами и ЭДС в ветвях электрической цепи и напряжениями на элементах цепи.

Задача 2.1.

Пользуясь законами Кирхгофа, рассчитать токи в ветвях схемы рис.2.1, если , , , , , , .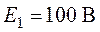

Решение.

1. Цепь рис. 2.1 содержит три ветви (), два узла (). Цепь питает два источника ЭДС и . И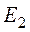сточники тока в цепи отсутствуют ().

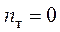Выберем произвольно положительные направления токов в ветвях схемы и обозначим их как указано на рис. 2.2.

Рис. 2.1. Рис. 2.2.

2. Определим достаточное количество уравнений для расчета цепи по законам Кирхгофа.

По первому закону Кирхгофа:

По второму закону Кирхгофа:

Достаточное количество уравнений равно трем, что соответствует количеству неизвестных токов, обозначенных в ветвях схемы как , 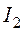и (рис. 2.2).

3. Составим систему уравнений по первому и второму закону Кирхгофа. Одно уравнение по первому закону Кирхгофа, например, для узла 1 и два уравнения по второму закону Кирхгофа для двух независимых контуров. Положительные направления обхода контуров соответствуют направлениям, указанным на рис. 2.2.

для узла 1: ;

для контура : ;

для контура : .

4. После подстановки числовых значений имеем:

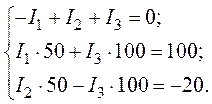
5. Решение системы получим с помощью определителей:

; ; ,

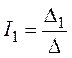где– главный определитель системы, , , – алгебраические дополнения.

Главный определитель системы равен:

Дополнительные определители равны:

;

6. Токи в ветвях:

; ; .

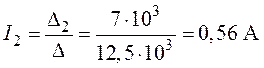Задача 2.2.

Рассчитать с использованием законов Кирхгофа токи в ветвях схемы изображенной на рис. 2.3, если известны , , 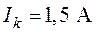, , , 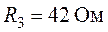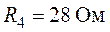. Выполнить правильность расчета цепи путем проверки баланса мощностей.

vunivere.ru

Примеры решения задач на законы Кирхгофа

Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.

Задача 1

Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.

Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.

На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.

Уравнения для первого и второго контуров по второму закону будут:

Все эти три уравнения образуют систему

Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).

Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.

Задача 2

Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2

Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.

На основании этих уравнений составляем систему с 5-ью неизвестными

Решив эту систему любым удобным способом, найдем неизвестные величины

Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.

Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.

Читайте также - расчет простых цепей постоянного тока

electroandi.ru

Методы расчета линейных электрических цепей

Расчет цепей с использованием законов Кирхгофа

Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы через b, число ветвей, содержащих источники тока, через bИT, число узлов - у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется (b - bИT). Перед тем как составлять уравнения, необходимо произвольно выбрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.

Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, т.е. у - 1. По второму закону Кирхгофа составляют число уравнений n , равное

n= b - bИT - (у - 1).

При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляются уравнения, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа, т.е. число уравнений по второму закону Кирхгофа равно числу независимых контуров.

Пример 1. Найти токи в ветвях схемы рис. 1.13, в которой Е1 = 80 В, Е2 = 64В, R1= 6 Ом, R2 = 4 Ом, R3 = 3 Ом, R4= 10 Ом.

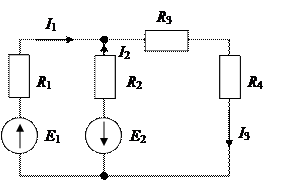
Рис. 1.13

Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме рис. 1.13 b=3; bИТ=0; y=2.

Следовательно, по первому закону Кирхгофа можно составить только одно уравнение y-1=1:

По второму закону Кирхгофа составим два уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.

Для контура R1E1R2E2

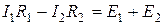Знак плюс перед I1R1 взят потому, что направление тока совпадает с направлением обхода контура, а знак минус перед I2R2 потому, что направление I2 встречно обходу контура.

Для контура E2R2R3R4:

Совместное решение трех уравнений дает

I1 = 14 A, I2 = -15 A, I3 = -1 A.

В рассматриваемом примере отрицательными оказались токи I2 и I3, это следует понимать так, что в действительности токи I2 и I3 направлены в обратную сторону.

Метод контурных токов

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.

Таким образом, метод контурных токов можно определить как метод расчета, в котором в качестве неизвестных принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, составляемых для схемы по второму закону Кирхгофа. Преимуществом этого метода, по сравнению с методом на основе законов Кирхгофа, является меньшая вычислительная работа, так как в нем меньше уравнений.

Вывод основных расчетных уравнений проведем применительно к схеме рис. 1.14, содержащей два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток I11 , а в правой (также по часовой) - контурный ток I22. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что в смежной ветви (с сопротивлением Rs) течет сверху вниз ток I11 - I22. Направления обхода контуров примем также по часовой стрелке.

Для первого контура

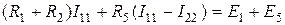
или

. (1.24)

Для второго контура

или

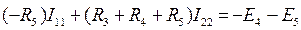. (1.25)

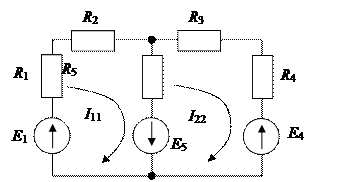
Рис. 1.14

В уравнении (1.24) множитель при токе I11, являющийся суммой сопротивлений первого контура, обозначим через R11, множитель при токе I22 (сопротивление смежной ветви, взятое со знаком минус), – через R12.

В уравнении (1.25) множитель при токе I22, являющийся суммой сопротивлений второго контура, обозначим через R22, множитель при токе I11 (сопротивление смежной ветви, взятое со знаком минус), – через R21.

Перепишем эти уравнения следующим образом:

Здесь

где R11 и R22 - полное или собственное сопротивление первого и второго контуров соответственно; E11 и Е22 - контурные ЭДС первого и второго контуров, равные алгебраической сумме ЭДС этих контуров; R12 = R21 -сопротивление смежной ветви между первым и вторым контуром, взятое со знаком минус, так как контурные токи по ветви протекают встречно.

Если в схеме больше контуров, например три, то система уравнений в общем виде выглядит следующим образом:

(1.26)

В результате решения системы уравнений (1.26) какой-либо один или несколько контурных токов могут оказаться отрицательными.

В ветвях, не являющихся смежными между соседними контурами, найденный контурный ток является истинным током ветви. В смежных ветвях через контурные токи определяются токи ветвей.

Если в электрической цепи имеется n независимых контуров, то число уравнений тоже равно n.

Общее решение системы n-уравнений относительно тока Ikk таково:

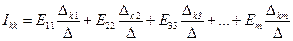, (1.27)

где D - определитель системы.

Алгебраическое дополнение ∆km, получено из определителя ∆ путем вычеркивания k-го столбца и m-й строки и умножения полученного определителя на (-1)k + m.

Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока. Если для схемы рис. 1.15 принять, что контурный ток I11 = J течет согласно направлению часовой стрелки по первой и второй ветвям, а контурный ток I22 = I3 замыкается также по часовой стрелке по второй и третьей ветвям, то, согласно методу контурных токов, получим только одно уравнение с неизвестным током I22: