Содержание
Условное обозначение резисторов на схемах
Резистор (англ. resistor, от лат. resisto—сопротивляюсь) — радиокомпонент, основное назначение которого
оказывать активное сопротивление электрическому току. Основные характеристики резистора — номинальное сопротивление и
рассеиваемая мощность. Наиболее широко используются постоянные резисторы, реже — переменные, подстроечные, а также резисторы,
изменяющие свое сопротивление под действием внешних факторов.
Постоянные резисторы бывают проволочными (из провода с высоким и стабильным удельным сопротивлением) и
непроволочными (с резистивным элементом, например, в виде тонкой пленки из оксида металла, пиролитического углерода и т. д.).
Однако на схемах их обозначают одинаково — в виде прямоугольника с линиями электрической связи, символизирующими выводы резистора (рис. 1).
Это условное графическое обозначение — основа, на которой строятся обозначения всех разновидностей резисторов.
Указанные на рис. 1 размеры резисторов установлены ГОСТом и их следует соблюдать при вычерчивании схем.
Рис.1. Условное обозначение резисторов
На схемах рядом с обозначением резистора (по возможности сверху или справа) указывают его условное буквенно-цифровое позиционное
обозначение и номинальное сопротивление. Позиционное обозначение состоит из латинской буквы R (Rezisto) и порядкового номера резистора но схеме.
Сопротивление от 0 до 999 Ом указывают числом без обозначения единицы измерения (51 Ом —> 51), сопротивления от 1 до 999 кОм — числом со строчной буквой к (100 кОм —> 100 к),
сопротивления от 1 до 999 МОм — числом с прописной буквой М (150 МОм —> 150 М).
Если же позиционное обозначение резистора помечено звездочкой (резистор R2* на рис.1), то это означает, что сопротивление указано ориентировочно
и при налаживании устройства его необходимо подобрать по определённой методике.
Номинальную рассеиваемую мощность указывают специальными значками внутри условного графического обозначения (рис. 2).
Рис.2. Обозначение мощности резисторов
Постоянные резисторы могут иметь отводы от резистивного элемента (рис. 3, а), причем, если необходимо, то символ резистора вытягивают в длину (рис. 3, б).
Рис.3. Обозначение постоянных резисторов с отводами
Переменные резисторы используют для всевозможных регулировок. Как правило, у такого резистора минимум три вывода:
два — от резистивного элемента, определяющего номинальное (а практически — максимальное) сопротивление, и
один — от переметающегося по нему токосъемника — движка. Последний изображают в виде стрелки, перпендикулярной длинной стороне
основного условного графического изображения (рис. 4, а). Для переменных резисторов в реостатном включении допускается использовать
условное графическое изображение рис. 4, б. Переменные резисторы с дополнительными отводами обозначаются так, как показано на
4, б. Переменные резисторы с дополнительными отводами обозначаются так, как показано на
рис. 4, е. Отводы у переменных резисторов показывают так же, как и у постоянных (см. рис. 3).
Рис.4. Обозначение переменных резисторов
Для регулирования громкости, тембра, уровня в стереофонической аппаратуре, частоты в измерительных генераторах сигналов применяют
сдвоенные переменные резисторы. На схемах условных графических изображений входящие в них резисторы стараются расположить возможно ближе друг к другу,
а механическую связь показывают либо двумя сплошными линиями, либо одной штриховой (рис. 5, а). Если же сделать этого не удается, т. е.
символы резисторов оказываются на удалении один от другого, то механическую связь изображают отрезками штриховой линии (рис. 5, б).
Принадлежность резисторов к сдвоенному блоку указывают в позиционном обозначении (R2.1 — первый резистор сдвоенного переменного резистора R2, R2. 2 — второй).
2 — второй).
Рис.5. Обозначение сдвоенных переменных резисторов
В бытовой аппаратуре часто применяют переменные резисторы, объединенные с одним или двумя выключателями.
Символы их контактов размещают на схемах рядом с условным графическим изображением переменного резистора и соединяют
штриховой линией с жирной точкой, которую изображают с той стороны обозначения, при перемещении к которой движок воздействует на выключатель, (рис. 6, а).
При этом имеется в виду, что контакты замыкаются при движении от точки, а размыкаются при движении к ней.
В случае если обозначение резистора и выключателя на схеме удалены один от другого, механическую связь показывают отрезками штриховых линий (рис. 6, б).
Рис.6. Обозначение переменных резисторов совмещенных с выключателем
Подстроенные резисторы — это разновидность переменных. Узел перемещения движка таких резисторов чаще всего приспособлен для управления
отверткой и не рассчитан на частые регулировки. Обозначение подстроечного резистора (рис. 7) наглядно отражает его назначение:
Обозначение подстроечного резистора (рис. 7) наглядно отражает его назначение:
практически это постоянный резистор с отводом, положение которого можно изменять.
Рис.7. Обозначение подстроечных резисторов
Из резисторов, изменяющих свое сопротивление под действием внешних факторов, наиболее часто используют терморезисторы
(обозначение RK) и варисторы (RU). Общим для условного графического изображения резисторов этой группы является знак нелинейного саморегулирования
в виде наклонной линии с изломом внизу (рис. 8).
Рис.8. Обозначение терморезисторов и варисторов
Для указания внешних факторов воздействия используют их общепринятые буквенные обозначения: f (температура), U (напряжение) и т. д.
Знак температурного коэффициента сопротивления терморсзисторов указывают только в том случае, если он отрицательный (см. рис. 8, резистор RK2).
Обозначение резисторов обозначение резисторов на схеме
Резистор представляет собой пассивный элемент, без которого практически неработоспособна любая электрическая схема. Основная задача данной детали – это осуществление линейных преобразований параметров электрического тока. Достаточно наглядно это можно уяснить из формулы закона Ома, которая для участка цепи имеет следующий вид — I=U/R. Изменяя значение R (характеризующее величину сопротивления) можно регулировать другие параметры электрического тока. Также литера «R» используется для обозначения резисторов на схеме.
Основная задача данной детали – это осуществление линейных преобразований параметров электрического тока. Достаточно наглядно это можно уяснить из формулы закона Ома, которая для участка цепи имеет следующий вид — I=U/R. Изменяя значение R (характеризующее величину сопротивления) можно регулировать другие параметры электрического тока. Также литера «R» используется для обозначения резисторов на схеме.
Необходимо отметить, что схематическое изображение сопротивления (резистора) в разных странах имеют разный вид. Так для зарубежной документации нередко используется фигура, изображенная на рис.1. Для отечественных электриков привычным является условное обозначение резисторов пример, которого приведен на рис.2.
Рассмотрим более подробно варианты и особенности обозначения
резисторов (сопротивлений), а также отображение их характеристик, свойственных
для электрических схем, которые используются в отечественной электротехнике.
Графические обозначения резисторов имеют строго определенный
вид, который определен ГОСТом 2..jpg) 728-74. Рассмотрим основные варианты
728-74. Рассмотрим основные варианты
изображений сопротивлений в зависимости от их типа. Итак, резисторы бывают:
— постоянными, т.е. их сопротивление в Омах не меняется. На
схемах они соответствуют примеру, изображенному на рис.2. В случае если
требуется указать величину номинального рассеяния мощности, то в УГО (условное
графическое изображение) вносятся некоторые изменения (рис.3).
Рис.3
— переменные резисторы. Эти элементы имеют плавную или
ступенчатую регулировку величины сопротивления. Обозначение на схемах
соответствуют рис.4.
Также в данном ГОСТе оговорены варианты обозначений для
резисторов:
- с симметричными и несимметричными отводами;
- с нелинейным регулированием;
- связанных и несвязанных механически;
- с замыкающим контактом и т.д.
Обозначение на схемах характеристик сопротивления резисторов
Основной характеристикой резистора является величина его сопротивления. На схемах этот параметр, как правило, располагается с буквенным обозначение «R» в виде цифр.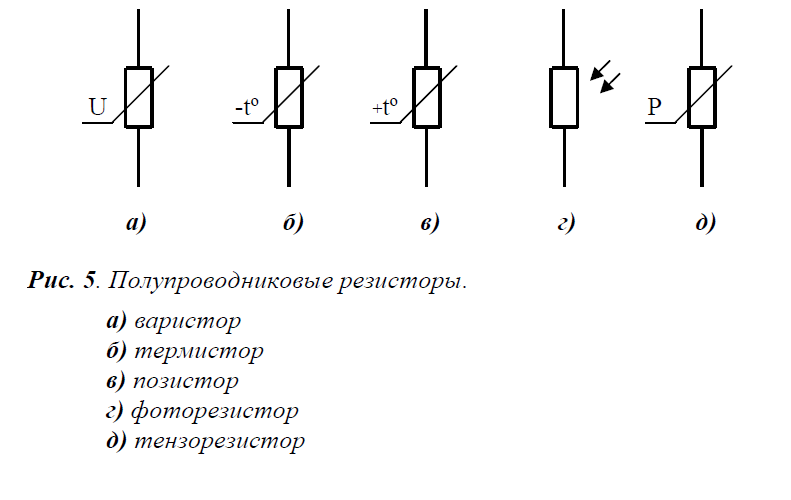 Есть небольшая особенность – если после числового номинала следует буквенная маркировка «К» или «М», то сопротивление данного резистора соответствует произведению данного числа на тысячу или миллион. Аналогично обозначается сопротивление и на корпусе самой детали, если площадь это позволяет. Иногда можно встретить маркировку другого вида, например, 2К4. Здесь все просто. Сопротивление данного резистора будет равно 2400 Ом. Более полную информацию по буквенно-цифровой маркировке можно посмотреть в табл.2 ГОСТа 28883-90 (МЭК 62-74).
Есть небольшая особенность – если после числового номинала следует буквенная маркировка «К» или «М», то сопротивление данного резистора соответствует произведению данного числа на тысячу или миллион. Аналогично обозначается сопротивление и на корпусе самой детали, если площадь это позволяет. Иногда можно встретить маркировку другого вида, например, 2К4. Здесь все просто. Сопротивление данного резистора будет равно 2400 Ом. Более полную информацию по буквенно-цифровой маркировке можно посмотреть в табл.2 ГОСТа 28883-90 (МЭК 62-74).
Сложнее обстоит дело, когда деталь имеет настолько маленькие
размеры, что нанести на корпус резистора его параметры технически невозможно.
Это также относиться к обозначению SMD резисторов, которые получили в
последнее время широкое распространение благодаря миниатюрным размерам. Используются
они для поверхностной пайки в электронных платах различных изделий.
Обозначение номиналов SMD резисторов
Данные типы резисторов отличаются по внешнему виду от
привычных изделий и как говорилось выше имеют минимальные размеры. Обозначение
Обозначение
номинала сопротивления SMD резисторов может осуществляться их буквенно-цифровой
маркировкой в следующих вариантах:
- трехзначное число. Первые две сообщают о величине сопротивления в Омах, а последняя является множителем. Проще говоря первые два числа умножаются на 10 в степени соответствующей последней цифре;
- четырехзначное число. Первые три цифры являются номиналом, а последняя множителем, как и в предыдущем случае;
- двухзначное число, дополненное буквенным индексом. Это наиболее непростой вариант и для выяснения номинала сопротивления такого SMD резистора необходимо воспользоваться специальной таблицей.
Цветовое обозначение характеристик резисторов
Идея маркировки резисторов цветами, появилась вследствие
минимизации их размеров и невозможности нанесения на корпус деталей
буквенно-цифрового кода. Данное обозначение наносится в виде полос или колец,
таким образом, чтобы характеристики детали можно было определить вне
зависимости от ее положения на плате или в электрической цепи устройства.
Требования к цветовому обозначение характеристик проволочных
резисторов изложены в ГОСТ 28883-90 (МЭК 62-74), а сами значения приведены в
таблице 1 данного документа.
Таблица 1 ГОСТ 28883-90
Количество цветных колец может колебаться от трех до шести.
Считывание необходимо начинать с той полосы которая расположена наиболее близко
к одному из контактов. В отдельных случаях, когда нет возможности нанести
маркировку с однозначной интерпретацией какой цвет является начальным, первый
цвет наносят в виде утолщённой в 2 раза полосы или кольца.
В заключение можно отметить, чтобы однозначно и правильно идентифицировать маркировку и обозначения характеристик резисторов необходимо обратиться к вышеуказанным нормативным документам. Также желательно отслеживать появление новых изменений в данную литературу, что является особенно актуальным в современных условиях развития электротехники и выпуску новых видов деталей, применяемых в электрических схемах приборов и устройств.
Добавить отзыв
6.3 Правила Кирхгофа. Введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу раздела вы сможете:
- Государственное правило пересечения Кирхгофа
- Государственное правило петли Кирхгофа
- Анализ сложных цепей с использованием правил Кирхгофа
Мы только что видели, что некоторые цепи можно анализировать, сводя цепь к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы невозможно проанализировать с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно остановимся на использовании правил Кирхгофа для анализа более сложных схем. Например, схема на рис. 6. 3.1 известна как многоконтурная схема , состоящая из узлов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы расположены последовательно или параллельно, и их можно уменьшить. Попробуйте. Резисторы и соединены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое верно для резисторов и . Но что вы делаете тогда?
3.1 известна как многоконтурная схема , состоящая из узлов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы расположены последовательно или параллельно, и их можно уменьшить. Попробуйте. Резисторы и соединены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое верно для резисторов и . Но что вы делаете тогда?
Несмотря на то, что эту цепь нельзя проанализировать с помощью уже изученных методов, для анализа любой цепи, простой или сложной, можно использовать два правила анализа цепей. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).
(рис. 6.3.1)
Рисунок 6.3.1 Эта схема не может быть сведена к комбинации последовательного и параллельного соединений. Однако мы можем использовать правила Кирхгофа для его анализа.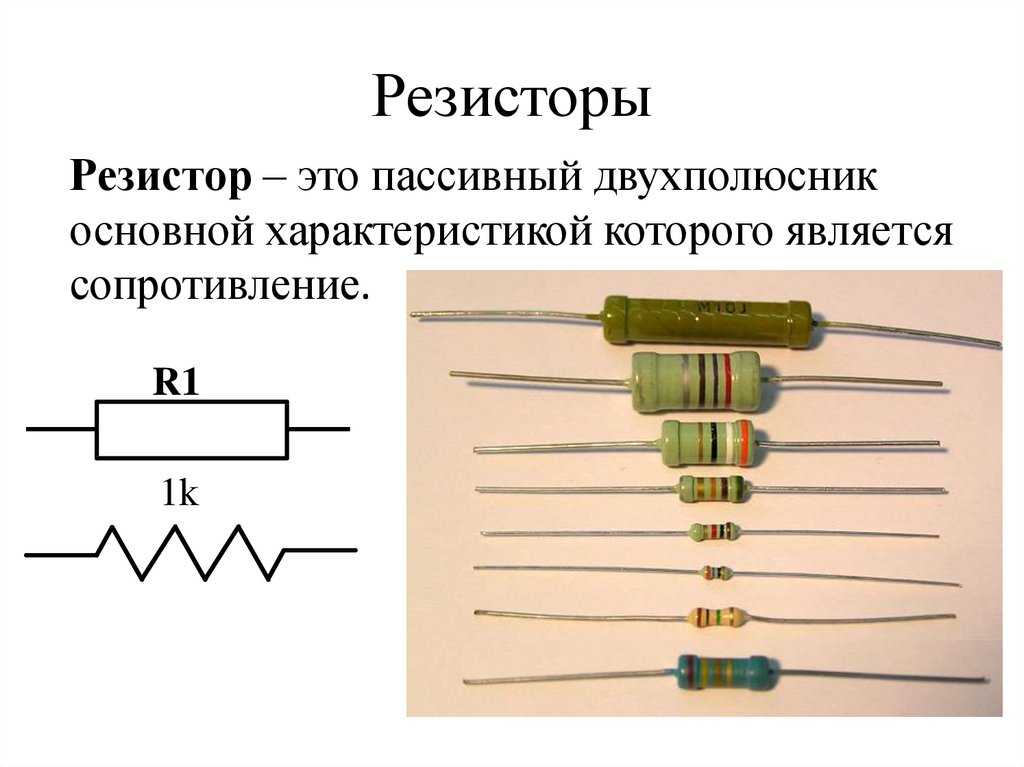
ПРАВИЛА КИРХГОФА
- Первое правило Кирхгофа — правило соединения . Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
(6.3.1)
- Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (контура) должна быть равна нулю:
(6.3.2)
Теперь мы даем объяснения этих двух правил, за которыми следуют советы по решению проблем по их применению и рабочий пример, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рис. 6.3.2). Как указывалось ранее, узел или узел — это соединение трех или более проводов. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу.
(рис. 6.3.2)
Рисунок 6. 3.2 Заряд должен сохраняться, поэтому сумма токов в соединении должна быть равна сумме токов вне соединения.
3.2 Заряд должен сохраняться, поэтому сумма токов в соединении должна быть равна сумме токов вне соединения.
Хотя это упрощение, можно провести аналогию с водопроводными трубами, соединенными в сантехническом узле. Если провода на Рисунке 6.3.2 были заменены водопроводными трубами, а вода считалась несжимаемой, объем воды, втекающей в соединение, должен равняться объему воды, вытекающей из соединения.
Второе правило Кирхгофа
Второе правило Кирхгофа ( петлевое правило ) применяется к разности потенциалов. Правило цикла сформулировано в терминах потенциальной, а не потенциальной энергии, но они связаны, поскольку . В замкнутом контуре, какая бы энергия ни поставлялась источником напряжения, энергия должна передаваться в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжения, подаваемые источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без соединений, как на рисунке 6.3.3.
Например, рассмотрим простую петлю без соединений, как на рисунке 6.3.3.
(рис. 6.3.3)
Рисунок 6.3.3 Простая петля без соединений. Правило цикла Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.
Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки , , , и служат ссылками и не имеют никакого другого значения. Полезность этих ярлыков скоро станет очевидной. Петля обозначена как Loop , а метки помогают отслеживать разность напряжений, когда мы перемещаемся по цепи. Начните с точки и двигайтесь к ней. К уравнению добавляется напряжение источника напряжения и вычитается падение потенциала на резисторе. От точки до вычитается падение потенциала. От до вычитается падение потенциала. От точек до ничего не делается, потому что нет компонентов.
На рис. 6.3.4 показан график изменения напряжения при перемещении по контуру. Напряжение увеличивается, когда мы пересекаем батарею, тогда как напряжение уменьшается, когда мы пересекаем резистор.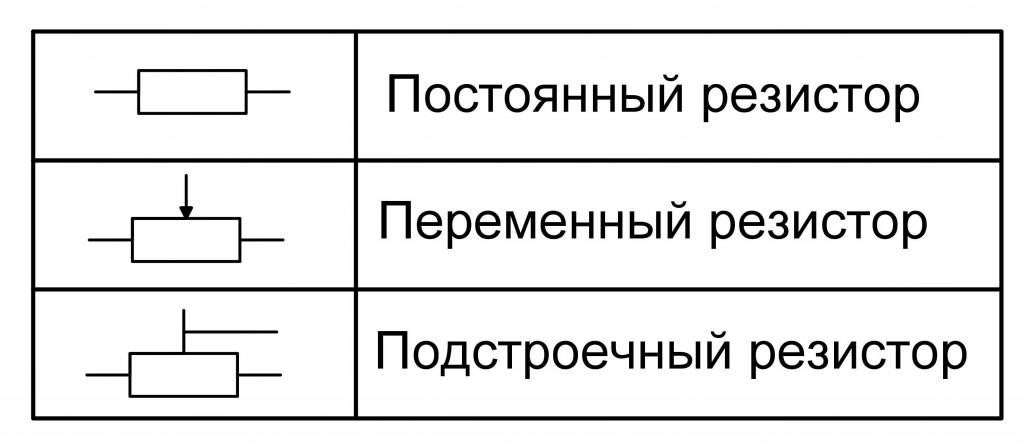 Падение потенциала или изменение электрического потенциала равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Падение потенциала или изменение электрического потенциала равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
(рис. 6.3.4)
Рисунок 6.3.4 График напряжения при перемещении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Тогда правило цикла Кирхгофа утверждает
Уравнение контура можно использовать для определения тока через контур:
Эту петлю можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем возможности метода Кирхгофа в следующем разделе.
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем набор линейных уравнений, которые позволяют нам находить неизвестные значения в цепях. Это могут быть токи, напряжения или сопротивления. Каждый раз, когда правило применяется, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема.
Это могут быть токи, напряжения или сопротивления. Каждый раз, когда правило применяется, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема.
Использование метода анализа Кирхгофа требует выполнения нескольких шагов, перечисленных в следующей процедуре.
Стратегия решения проблем: правила Кирхгофа
- Обозначьте точки на принципиальной схеме строчными буквами. Эти метки просто помогают с ориентацией.
- Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток указывает на соединение и по крайней мере один ток указывает на соединение.
- Выберите петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
- Применить правило соединения. Опять же, некоторые соединения не должны быть включены в анализ.
 Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий.
Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий. - Применить правило цикла. Используйте карту на рисунке 6.3.5.
(рис. 6.3.5)
Рисунок 6.3.5 Каждый из этих резисторов и источников напряжения проходит от до . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном течению тока, добавьте падение потенциала. (c) При перемещении через источник напряжения от отрицательной клеммы к положительной клемме добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной клемме вычтите падение потенциала.
Рассмотрим некоторые шаги этой процедуры более подробно. При нахождении соединений в цепи не беспокойтесь о направлении токов. Если направление протекания тока неочевидно, достаточно выбрать любое направление, если по крайней мере один ток указывает на соединение, а по крайней мере один ток направлен из соединения. Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.
См. рис. 6.3.6. В этой цепи есть два соединения: соединение и соединение . Точки , , и не являются соединениями, потому что соединение должно иметь три или более соединений. Уравнение для соединения , а уравнение для соединения . Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
(рис. 6.3.6)
Рисунок 6.3.6 На первый взгляд, эта схема содержит два соединения, Соединение и Соединение , но следует рассматривать только одно, поскольку их уравнения соединения эквивалентны.
При выборе петель в схеме нужно столько петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 6.3.7 показаны четыре варианта циклов для решения примера схемы; варианты (a), (b) и (c) имеют достаточное количество циклов, чтобы полностью решить схему. Вариант (г) отражает больше циклов, чем необходимо для решения схемы.
На рис. 6.3.7 показаны четыре варианта циклов для решения примера схемы; варианты (a), (b) и (c) имеют достаточное количество циклов, чтобы полностью решить схему. Вариант (г) отражает больше циклов, чем необходимо для решения схемы.
(рис. 6.3.7)
Рисунок 6.3.7 Панели (a)–(c) достаточны для анализа цепи. В каждом случае две показанные петли содержат все элементы схемы, необходимые для полного решения схемы. На панели (d) показаны три использованные петли, что больше, чем необходимо. Любые два цикла в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла обеспечивает избыточную информацию.
Рассмотрим схему на рис. 6.3.8(а). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала пометьте схему, как показано в части (b).
(рис. 6.3.8)
Рисунок 6.3.8 (a) Многоконтурная схема. (b) Подпишите схему, чтобы помочь с ориентацией.
Далее определите развязки. В этой схеме точки и соединены по три провода, что делает их соединениями. Начните применять правило соединения Кирхгофа, нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 6.3.9 (b). Junction показывает это, а Junction показывает это. Поскольку Junction предоставляет ту же информацию, что и Junction , ею можно пренебречь. В этой схеме три неизвестных, поэтому для ее анализа нам нужны три линейно независимых уравнения.
В этой схеме точки и соединены по три провода, что делает их соединениями. Начните применять правило соединения Кирхгофа, нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 6.3.9 (b). Junction показывает это, а Junction показывает это. Поскольку Junction предоставляет ту же информацию, что и Junction , ею можно пренебречь. В этой схеме три неизвестных, поэтому для ее анализа нам нужны три линейно независимых уравнения.
(рис. 6.3.9)
Рисунок 6.3.9 (a) Эта схема имеет два соединения, обозначенных b и e, но в анализе используется только узел b. (б) Маркированные стрелки представляют токи в и из соединений.
Далее нам нужно выбрать петли. На рис. 6.3.10 контур включает в себя источник напряжения, резисторы и . Цикл начинается с точки , затем проходит через точки , , и , а затем возвращается к точке . Второй контур, Loop , начинается в точке и включает резисторы и и источник напряжения .
(рис. 6.3. 10)
10)
Рисунок 6.3.10 Выберите петли в цепи.
Теперь мы можем применить правило цикла Кирхгофа, используя карту на рис. 6.3.5. Начиная с точки и двигаясь к точке, сопротивление пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. Перемещаясь от точки к точке, резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. При переходе от точки к точке источник напряжения пересекается с отрицательной клеммы на положительную, поэтому добавляется . Между точками и 9 нет компонентов0146 . Сумма разностей напряжений должна быть равна нулю:
Наконец, мы проверяем цикл. Мы начинаем с точки и движемся к ней, пересекая ее в направлении, противоположном текущему потоку. Потенциальное падение добавлено. Затем мы пересекаем и в том же направлении, что и текущий поток , и вычитаем падения потенциала и . Обратите внимание, что ток через резисторы и одинаков, поскольку они соединены последовательно.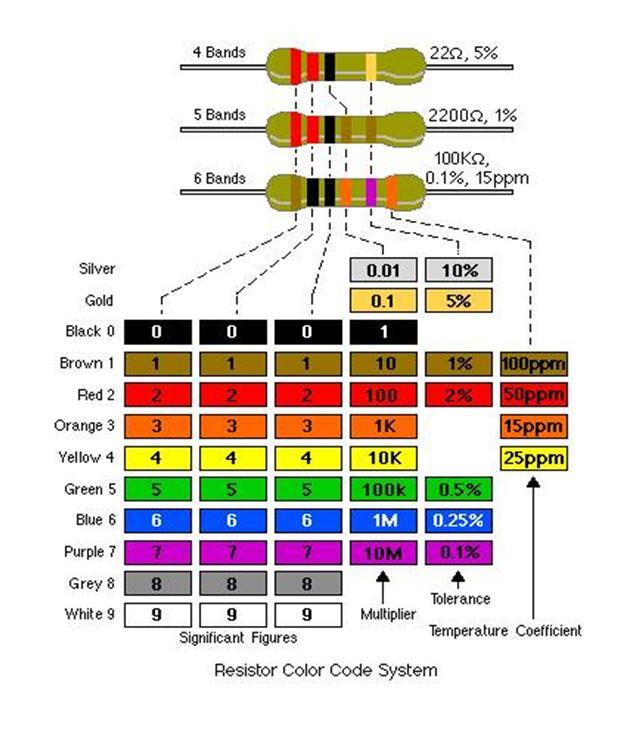 Наконец, источник напряжения пересекается с положительной клеммы на отрицательную клемму, и источник напряжения вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура
Наконец, источник напряжения пересекается с положительной клеммы на отрицательную клемму, и источник напряжения вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура
Теперь у нас есть три уравнения, которые мы можем решить для трех неизвестных.
Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока . Сначала добавьте уравнение (1) раз к уравнению (2). Результат помечен как уравнение. (4):
Далее вычтите уравнение (3) из уравнения (2). Результат помечен как уравнение. (5):
Мы можем решить уравнения. (4) и (5) для тока . Складывая семь раз уравнение (4) и трижды уравнение. (5) приводит к , или . Используя уравнение (4) приводит к . Наконец, уравнение (1) дает . Один из способов проверить согласованность решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
Обратите внимание, что решение для текущего отрицательно. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединения, указывает направление, противоположное обычному протеканию тока. Мощность, подаваемая вторым источником напряжения, равна и не равна .
Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединения, указывает направление, противоположное обычному протеканию тока. Мощность, подаваемая вторым источником напряжения, равна и не равна .
ПРИМЕР 6.3.1
Расчет тока с использованием правил Кирхгофа
Найдите токи, протекающие в цепи на рисунке 6.3.11.
(рис. 6.3.11)
Рисунок 6.3.11 Эта схема представляет собой комбинацию последовательных и параллельных конфигураций резисторов и источников напряжения. Эту цепь нельзя проанализировать с помощью методов, описанных в разделе «Электродвижущая сила», но ее можно проанализировать с помощью правил Кирхгофа.
Стратегия
Эта цепь настолько сложна, что токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Течения обозначены на рисунке , и , и сделаны предположения об их направлениях.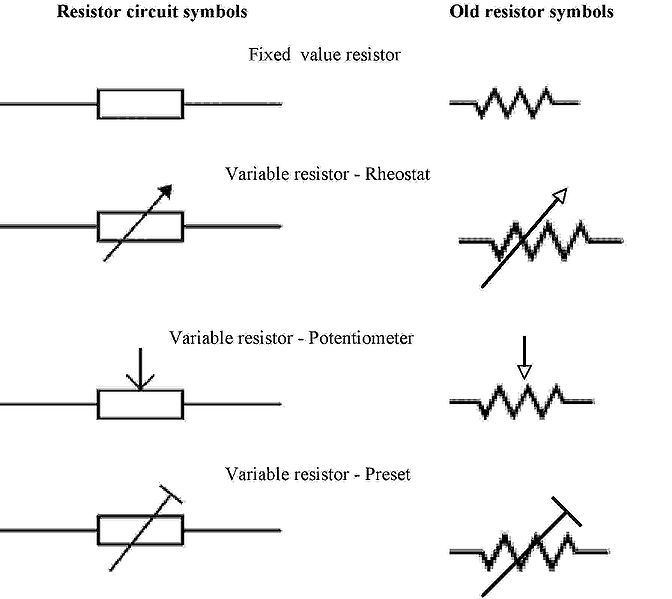 Места на схеме обозначены буквами от до . В решении мы применяем правила соединения и петли, ищем три независимых уравнения, которые позволяют нам найти три неизвестных тока.
Места на схеме обозначены буквами от до . В решении мы применяем правила соединения и петли, ищем три независимых уравнения, которые позволяют нам найти три неизвестных тока.
Решение
Применение правил соединения и петли приводит к следующим трем уравнениям. У нас есть три неизвестных, поэтому требуется три уравнения.
Упростите уравнения, поместив неизвестные в одну сторону уравнений.
Упростите уравнения. Первое уравнение контура можно упростить, разделив обе части на . Второе уравнение цикла можно упростить, разделив обе части на .
Результат
Значение
Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, выдаваемой источниками напряжения:
Подводимая мощность равна мощности, рассеиваемой резисторами.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.6
При рассмотрении следующей схемы и мощности, подаваемой и потребляемой цепью, будет ли источник напряжения всегда обеспечивать питание цепи или источник напряжения может потреблять энергию?
ПРИМЕР 6.3.2
Расчет силы тока с помощью правил Кирхгофа
Найдите ток, протекающий в цепи на Рисунке 6.3.12.
(рис. 6.3.12)
Рисунок 6.3.12 Эта схема состоит из трех резисторов и двух батарей, соединенных последовательно. Обратите внимание, что батареи подключены с противоположной полярностью.
Стратегия
Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только одна петля и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки к точке . Рассмотрите цикл и используйте рисунок 6.3.5, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 6.3.5 батарея будет добавлена, а батарея вычтена.
Решение
Применение правила соединения приводит к следующим трем уравнениям. У нас есть одно неизвестное, поэтому требуется одно уравнение:
Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.
Значение
Мощность, рассеиваемая или потребляемая цепью, равна мощности, подаваемой в цепь, но обратите внимание, что ток в батарее протекает через батарею от положительной клеммы к отрицательной клемме и потребляет энергию.
Подводимая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.7
При использовании законов Кирхгофа необходимо решить, какие контуры использовать и направление тока через каждый контур. При анализе схемы в примере 6.3.2 направление тока было выбрано по часовой стрелке, от точки a до точки b . Как изменились бы результаты, если бы направление тока было выбрано против часовой стрелки, от точки к точке?
Несколько источников напряжения
Для многих устройств требуется более одной батареи.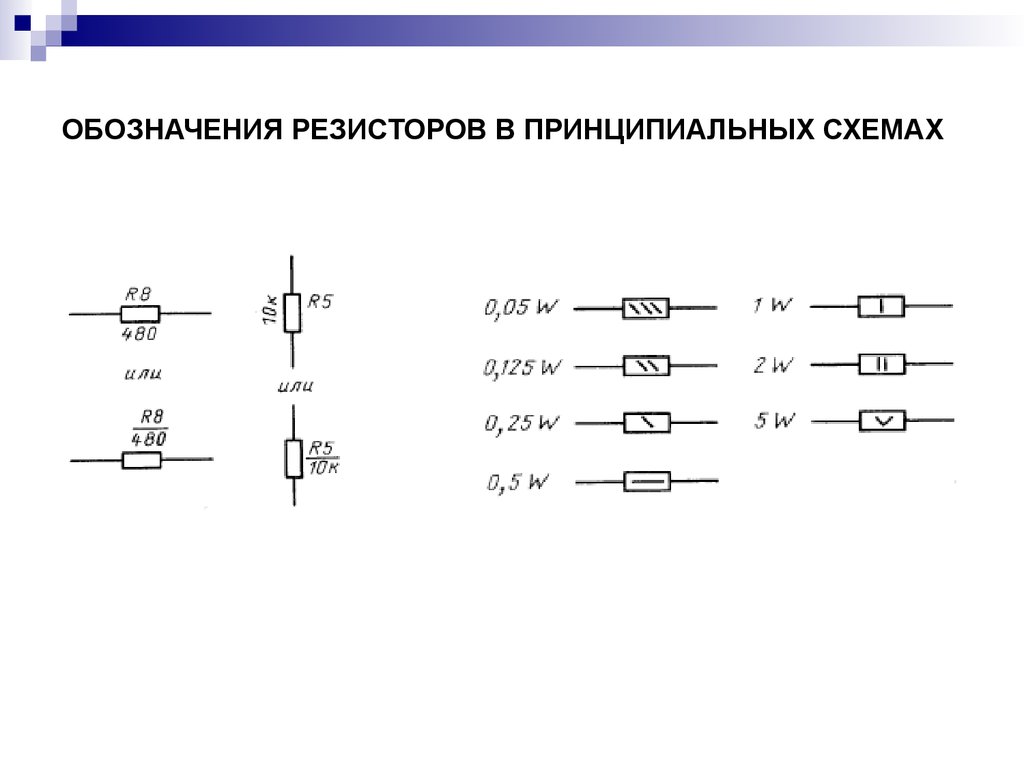 Несколько источников напряжения, таких как батареи, могут быть соединены последовательно, параллельно или в комбинации.
Несколько источников напряжения, таких как батареи, могут быть соединены последовательно, параллельно или в комбинации.
Последовательно положительная клемма одной батареи подключается к отрицательной клемме другой батареи. Любое количество источников напряжения, включая батареи, может быть соединено последовательно. Две батареи, соединенные последовательно, показаны на рисунке 6.3.13. Использование правила цикла Кирхгофа для схемы в части (b) дает результат
(рис. 6.3.13)
Рисунок 6.3.13 (a) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, где каждая батарея смоделирована как идеализированный источник ЭДС и внутреннее сопротивление.
Когда источники напряжения соединены последовательно, их внутренние сопротивления могут быть сложены вместе, а их ЭДС могут быть сложены вместе, чтобы получить общие значения. Распространены последовательные соединения источников напряжения, например в фонарях, игрушках и др.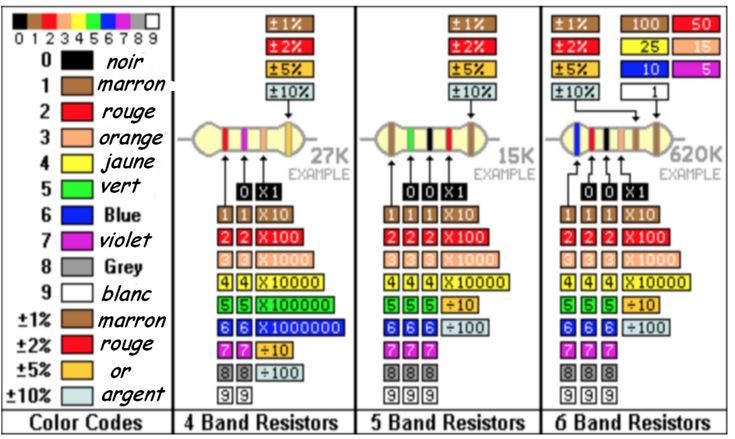 приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС. На рисунке 6.3.13 напряжение на клеммах равно
приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС. На рисунке 6.3.13 напряжение на клеммах равно
Обратите внимание, что в каждой батарее присутствует одинаковый ток, поскольку они соединены последовательно. Недостатком последовательного соединения ячеек является аддитивность их внутренних сопротивлений.
Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батарейки типа ААА, каждая с напряжением на клеммах 10 000 000 000 ₽, чтобы питать фонарик.
Любое количество аккумуляторов может быть соединено последовательно. Для батарей, соединенных последовательно, напряжение на клеммах равно
(6.3.3)
, где эквивалентное сопротивление равно .
Когда нагрузка подключена к источникам напряжения последовательно, как показано на рисунке 6.3.14, мы можем найти ток:
Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.
(рис. 6.3.14)
Рисунок 6.3.14 Две батареи соединены последовательно со светодиодной лампочкой, как в фонарике.
Источники напряжения, такие как батареи, также могут быть подключены параллельно. На рис. 6.3.15 показаны две батареи с одинаковыми ЭДС, подключенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи соединены параллельно, положительные клеммы соединены вместе, а отрицательные клеммы соединены вместе, а сопротивление нагрузки подключено к положительной и отрицательной клеммам. Обычно параллельно подключенные источники напряжения имеют одинаковые ЭДС. В этом простом случае, поскольку источники напряжения параллельны, общая ЭДС такая же, как и отдельные ЭДС каждой батареи.
(рис. 6.3.15)
Рисунок 6.3.15 (a) Две батареи подключены параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея в качестве источника ЭДС и внутреннего резистора. Два источника ЭДС имеют одинаковые ЭДС (каждый из которых помечен ), соединенные параллельно, которые производят одинаковую ЭДС.
Рассмотрим анализ Кирхгофа схемы на рис. 6.3.15(b). В точках и есть две петли и узел.
Решение для тока через нагрузочный резистор дает , где . Напряжение на клеммах равно падению потенциала на нагрузочном резисторе. Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.
Параллельно можно соединить любое количество аккумуляторов. Для батарей, соединенных параллельно, напряжение на клеммах равно
(6.3.4)
, где эквивалентное сопротивление равно .
Например, некоторые дизельные грузовики используют две батареи параллельно; они производят общую ЭДС, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.
Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме отдельных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют одинаковую ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше отдельных внутренних сопротивлений. Батареи соединены последовательно, чтобы увеличить напряжение на клеммах нагрузки. Батареи соединены параллельно для увеличения тока нагрузки.
Батареи соединены последовательно, чтобы увеличить напряжение на клеммах нагрузки. Батареи соединены параллельно для увеличения тока нагрузки.
Солнечные батареи
Другим примером, связанным с несколькими источниками напряжения, является комбинация солнечных элементов , соединенных как последовательно, так и параллельно для получения желаемого напряжения и тока. Фотоэлектрическая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте. Фотоэлектрический эффект выходит за рамки этого учебника, но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают электрический ток в элементе.
Большинство солнечных элементов сделаны из чистого кремния. Большинство отдельных ячеек имеют выходное напряжение около 100 мА, а выходной ток зависит от количества солнечного света, падающего на ячейку (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические клетки производят ток на единицу площади, составляющий около площади поверхности клетки.
Отдельные солнечные элементы электрически соединены в модули для удовлетворения потребностей в электроэнергии. Их можно соединить последовательно или параллельно, как батареи, о которых говорилось ранее. Массив или модуль солнечных элементов обычно состоит из ячеек между и с выходной мощностью до .
Солнечные элементы, как и батареи, обеспечивают напряжение постоянного тока. Ток от источника постоянного напряжения является однонаправленным. Большинству бытовых приборов требуется переменный ток (ac) напряжения.
Цитаты Кандела
Лицензионный контент CC, указание конкретного автора
- Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Принципы Кирхгофа — Nexus Wiki
Разработанные нами основные идеи о движении электрических зарядов в материи служат основой для анализа широкого спектра электрических цепей и устройств, а также для моделирования электрического поведения биологических систем. Но эти схемы, устройства и модели могут быстро стать довольно сложными.
Но эти схемы, устройства и модели могут быстро стать довольно сложными.
Полезно составить набор из опорных идей — принципов, за которые мы можем держаться и на которые можно ссылаться, чтобы организовать наше мышление в сложных ситуациях. — предоставлять «ставки в земле», которым мы можем доверять и использовать для поддержки нашей системы безопасности последовательных и связанных идей.
Основополагающие принципы понимания электрических токов были разработаны немецким физиком XIX века Густавом Кирхгофом (да, две буквы «h») называются законами (или принципами) Кирхгофа. (Он также сформулировал законы спектроскопии и термохимии.)
(Идеализированный) контекст для принципов Кирхгофа
Принципы Кирхгофа являются ограничениями более общих электромагнитных законов (уравнения Максвелла, сохранение заряда) на стандартные ситуации в электрических цепях. Мы поговорим о них и будем использовать их в контексте анализа подключенных сетей электрических устройств — аккумуляторов, резисторов, конденсаторов и проводов. Вот как мы будем представлять и идеализировать их:
Вот как мы будем представлять и идеализировать их:
| Аккумуляторы — устройства, которые поддерживают постоянную разницу электрического давления (напряжения) на своих клеммах: подобно водяному насосу, который поднимает воду на определенную высоту. Мы используем символ, показанный справа, с более длинной линией, соответствующей концу батареи с более высоким потенциалом. | ||
| Резисторы — устройства, обладающие значительным лобовым сопротивлением и противодействующие току. Давление на них будет падать, когда через них протекает ток. Резистор, показанный на рисунке, относится к типу резисторов, используемых в самодельных электрических схемах. Полосы представляют собой цветовой код, который указывает размер резистора и его точность. Мы обозначаем их символом зигзага, показанным справа. | ||
Конденсаторы — устройства, которые могут поддерживать разделение зарядов в ответ на перепад давления (напряжение), приложенный к его пластинам. Символом конденсатора является пара параллельных линий, показанных справа. Обязательно различайте символ конденсатора (параллельные линии одинаковой длины) и батареи (параллельные линии разной длины)! Символом конденсатора является пара параллельных линий, показанных справа. Обязательно различайте символ конденсатора (параллельные линии одинаковой длины) и батареи (параллельные линии разной длины)! | ||
| Провода — проводники, соединяющие другие устройства. Мы относимся к ним как к идеальным проводникам; то есть как имеющий нулевое сопротивление. Это приближение работает только тогда, когда в цепи есть другие резисторы, имеющие значительное сопротивление, по сравнению с которым сопротивление проводов ничтожно мало. Символ провода — это просто линия, и она может быть прямой или изогнутой — без разницы. |
Кирхгофа 1
st (Flow) Принцип
Первый принцип представляет собой комбинацию двух идей:
- сохранение заряда (общее количество положительных зарядов минус общее количество отрицательных зарядов является константой)
- в электрических цепях из-за сильных сил отталкивания между одноименными зарядами электрические элементы остаются нейтральными — нигде не происходит накопления заряда.

Этот принцип часто называют «правилом потока» и формулируется следующим образом:
Общее количество тока, втекающего в любой объем электрической сети, равно количеству вытекающего.
Из нашего анализа того, как работают конденсатор и резистор, мы знаем, что эта идея не работает, когда все только начинается.
Например, когда мы заряжаем конденсатор, заряд течет в одну сторону конденсатора и выходит из другой: заряд (противоположного знака) накапливается на каждой пластине конденсатора в нарушение правила потока. Но если мы поместим вокруг конденсатора коробку и не заглянем внутрь, правило все равно сработает. Это также работает, когда система находится в устойчивом состоянии и все стабилизировалось.
То же самое относится и к резистору. Когда ток только начинает нарастать через резистор, накопление одинаковых и противоположных зарядов на двух концах резистора отвечает за создание электрического поля в резисторе (создание падения потенциала на резисторе), которое удерживает заряды, движущиеся через сопротивление резистора с постоянной скоростью, в соответствии с законами движения Ньютона.
В обоих этих случаях, когда мы подключаем эти устройства к цепи, нарушения принципа потока (накопление несбалансированных зарядов), происходящие внутри устройства, происходят быстро — за наносекунды или меньше. И если мы рассмотрим все устройство, а не только его часть, принцип все еще работает даже в этом временном масштабе.
Принцип Кирхгофа 2
nd (Сопротивление)
Второй принцип говорит о том, что происходит, когда через резистор протекает ток: в направлении тока происходит падение потенциала, пропорциональное умножению тока на свойство резистора. резистор. Это закон Ома , и он справедлив для любого устройства, в котором сопротивление потоку пропорционально скорости. (См. Резистивный электрический поток — закон Ома.) Мы можем даже увеличить его достоверность, если допустим, что сопротивление является функцией тока. В основном, нам не нужно это делать.
В резисторе ток через него пропорционален падению потенциала на нем : $ΔV = IR$ .
Обратите внимание, что здесь нужно быть немного осторожным. Это справедливо ТОЛЬКО для резистора. Это НЕ обязательно верно для группы подключенных резисторов. Если мы хотим иметь дело с группой резисторов и поместить вокруг нее коробку, представляя, что это один резистор, мы должны выяснить, каково эффективное сопротивление комбинации, используя комбинированные принципы. (См. Пример: Резисторы, соединенные последовательно и Пример: Резисторы, соединенные параллельно.)
Третий принцип Кирхгофа (Контур)
Если первый принцип Кирхгофа управляет током в электрической сети, то второй принцип касается падения напряжения в сети.
Мы можем понять это, используя аналогию с водой. (См. Способы думать о токе: Набор инструментов моделей.) Электрический потенциал в модели воды аналогичен высоте, на которую вода была поднята. Одна из вещей, которые мы знаем о высотах, заключается в том, что если вы сделаете петлю и вернетесь к той же точке, с которой начали, вы окажетесь на той же высоте, с которой начали. Какие бы падения (спуски) вы ни делали, их нужно было компенсировать равной суммой подъемов (подъемов), чтобы вернуться в исходную точку.
Какие бы падения (спуски) вы ни делали, их нужно было компенсировать равной суммой подъемов (подъемов), чтобы вернуться в исходную точку.
То же самое относится и к электрическому потенциалу (напряжению). Когда мы путешествуем по цепи, у нас могут быть подъемы, скажем, если мы проходим через батарею от ее нижнего конца к ее верхнему концу, и у нас могут быть падения, скажем, если мы проходим через сопротивление в направлении тока. Третий принцип Кирхгофа гласит:
При обходе любой петли в электрической сети потенциал должен вернуться к одному и тому же значению (сумма падений = сумма подъемов).
Это может быть немного сложно применить! Точно так же, как если вы поднимаетесь на холм, вы поднимаетесь, но если вы спускаетесь с того же холма, вы спускаетесь, будет ли у вас подъем или падение электрического потенциала, когда вы проходите через устройство, зависит от того, как вы следуете своей петле. Если вы пройдете через батарею от положительного конца к отрицательному, это даст вам каплю! Если вы пройдете через резистор в направлении, противоположном направлению тока, вы получите повышение! Когда вы оцениваете 2 9
Полезная эвристика
Применение принципов Кирхгофа к сложной схеме иногда бывает сложным.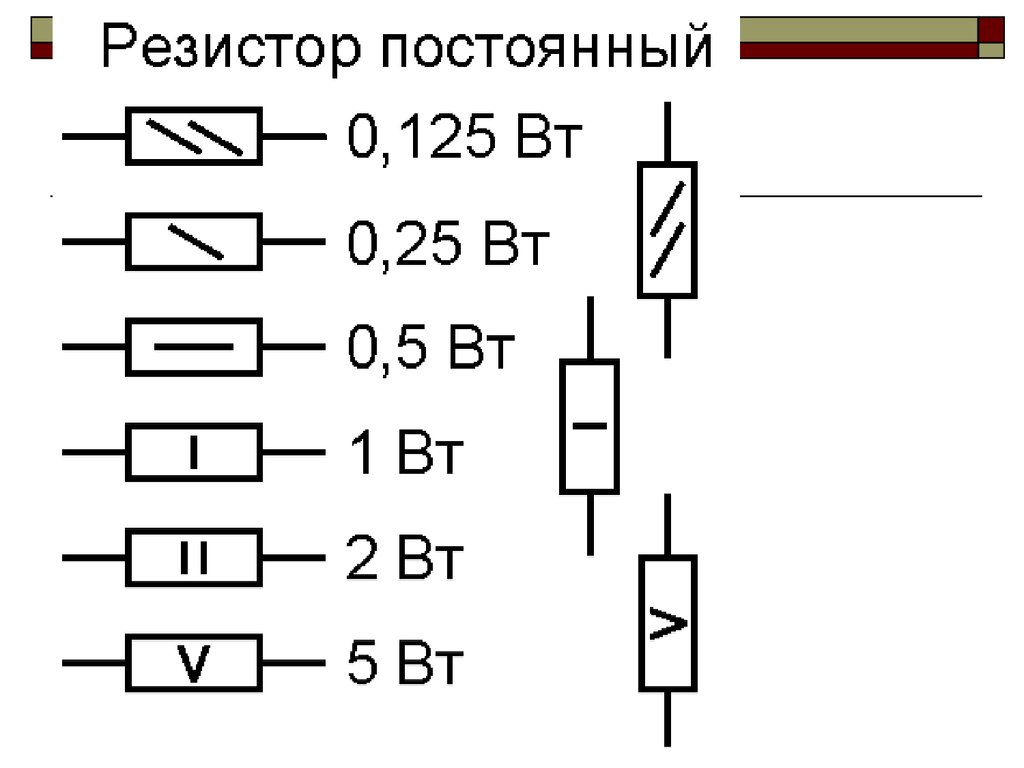 Необходимо решить две переменные — напряжение (электрическое давление) и ток. Это независимые переменные. Они влияют друг на друга, но ваша интуиция относительно того, что происходит, иногда относится к одному, иногда к другому — но легко запутаться!
Необходимо решить две переменные — напряжение (электрическое давление) и ток. Это независимые переменные. Они влияют друг на друга, но ваша интуиция относительно того, что происходит, иногда относится к одному, иногда к другому — но легко запутаться!
Удобный способ думать о напряжении во всей цепи аналогично давлению (в модели воздушного потока) или высоте (в модели водяного потока). По всей цепи перемещаются разные значения этой переменной — напряжения (электрического давления) — но она не движется и не изменяется. это разница между напряжениями (скажем, на противоположных концах резистора), которая управляет током через резистор.
Один из лучших способов начать анализ электрической сети — выяснить, что вы знаете о напряжении. А вот следствие из закона Ома, которое очень помогает при анализе сложных сетей:
Проводник в цепи, сопротивление которого можно рассматривать как имеющее 0 (например, провод), является эквипотенциальным (он имеет одинаковое значение потенциала на всей его длине), даже если по нему протекает ток.
 Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий.
Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий.