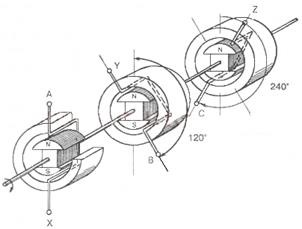
Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока. Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока. В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой. Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б. Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°. Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает Рис. 3.4. Пример трехфазной системы переменного тока а) генератор трёхфазного тока; б) с тремя генераторами; изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°. Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку. Соединение звездой Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы - X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева). Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф. Соединение треугольником. При использовании данного способа соединения конец X первой обмотки генератора подключают к началу В второй его обмотки, конец Y второй обмотки - к началу С третьей обмотки, конец Z третьей обмотки - к началу А первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл Контрольные вопросы 1. Перечислите основные параметры, характеризующие переменный ток. 2. Дайте определение частоты и единицы её измерения. 3. Дайте определение амплитуды и единицы её измерения. 4. Дайте определение периода и единицы его измерения. 5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока. 6. Что такое фаза? 7. Что представляет собой ротор генератора трёхфазного тока? 8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока? 9. Особенность симметричной системы трёх фаз. 10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда». 11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник». 3.2. Виды сопротивлений в цепях переменного тока В цепях переменного тока сопротивления разделяют на активные и реактивные. В активных сопротивлениях , включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R обладают, например, провода электрических линий, обмотки электрических машин и т.д. В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости. Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C. Активное сопротивление в цепи переменного тока . При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt . Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б). Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R. Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения u : p=ui . Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i , напряжения u и мощности p (б) и векторная диаграмма. Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности положительные, это означает, что энергия передается от источника к потребителю. Средняя мощность Рcp , потребляемая активным сопротивлением, P=UI=I 2 R – это и есть активная мощность. Под индуктивностью L будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис.3.8). При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э.д.с. самоиндукции e L = LΔi/Δt, где Δi/Δt – скорость изменения тока. Когда угол ωt равен 90° и 270° скорость изменения тока Δi/Δt =0, поэтому э.д.с. e L =0. Скорость изменения тока будет наибольшей, когда угол ωt равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение. Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью. Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i , напряжения u , э.д.с. e L (б) и векторная диаграмма (в) Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока). Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током). В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение. В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение. В результате ток отстает от напряжения по фазе на угол 90 О. Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением Х L [Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника. В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно. При последовательном соединении катушек эквивалентная индуктивностьLэ и эквивалентное индуктивное сопротивление X L э будут равны: Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +… При параллельном соединении катушек: 1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +… Контрольные вопросы 1. Какие виды сопротивления в цепях переменного тока Вы знаете? 2. Что значит активное сопротивление? 3. Что такое реактивное сопротивление? 4. Какие элементы цепи создают реактивное сопротивление? 5. Что такое активная мощность? 1. Дайте определение индуктивности. 2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью? 3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью? 4. Дайте определение индуктивного сопротивления. 3.3. Конденсаторы. Ёмкость в цепи переменного тока Конденсатор – устройство, способное накапливать электрические заряды. Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком. Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной). Cтраница 2 Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток. Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток. Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В. Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока. До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ. Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока. Рх o jjFr В слУчае т - н - СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по. Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх - / /, где РЯ - мощность eW, ra - активное сопротивление антенны в Q и 1а - действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика. Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 - 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др. Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 - 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями. В данном случае колебания тока являются гармоническими (график колебаний - синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником - генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки - от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность - минус. Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12.1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля - Ленца (Q I2Rt), определяем действующее значение силы тока (отв. Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока. Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе. Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токе Сила тока в цепи изменяется по синусоидальному закону Опуская вычисления, связанные с интегрированием, запишем окончательный результат Если бы по цепи шёл некоторый постоянный ток Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током: Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В. Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен Тогда мгновенное значение мощности, выделяемой на участке цепи, Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний): С использованием известной тригонометрической формулы Величину За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением Если участок цепи содержит несколько элементов, то сдвига фаз Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением Решение. Когда к генератору подключено одно только активное сопротивление Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора: В результате средняя расходуемая генератором мощность Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза. Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора Тогда средняя мощность, расходуемая генератором Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется. acost.ru Материал из Википедии — свободной энциклопедии Сила тока — физическая величина I{\displaystyle I}, равная отношению количества заряда ΔQ{\displaystyle \Delta Q}, прошедшего через некоторую поверхность за время Δt{\displaystyle \Delta t}, к величине этого промежутка времени[1]: В качестве рассматриваемой поверхности часто используется поперечное сечение проводника. Обычно обозначается символом I{\displaystyle I}, от фр. intensité du courant. Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ. 1 А = 1 Кл/с. По закону Ома сила тока I{\displaystyle I} для участка цепи прямо пропорциональна приложенному напряжению U{\displaystyle U} к участку цепи и обратно пропорциональна сопротивлению R{\displaystyle R} проводника этого участка цепи: По закону Ома для полной цепи Носителями заряда, движение которых приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступают электроны, ионы или дырки. Сила тока зависит от заряда q{\displaystyle q} этих частиц, их концентрации n{\displaystyle n}, средней скорости упорядоченного движения частиц vcp→{\displaystyle {\vec {v_{cp}}}}, а также площади S{\displaystyle S} и формы поверхности, через которую течёт ток. Если n{\displaystyle n} и vcp→{\displaystyle {\vec {v_{cp}}}} постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде где α{\displaystyle \alpha } — угол между скоростью частиц и вектором нормали к поверхности. В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока dI{\displaystyle dI}, протекающего через малый элемент поверхности площадью dS{\displaystyle dS}: Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид где e{\displaystyle e} — элементарный электрический заряд. Вектор qnvcp→{\displaystyle qn{\vec {v_{cp}}}} называют плотностью электрического тока. Как следует из сказанного выше, его величина равна силе тока, протекающей через малый элемент поверхности единичной площади, расположенный перпендикулярно скорости vcp→{\displaystyle {\vec {v_{cp}}}}, а направление совпадает с направлением упорядоченного движения заряженных частиц[2]. Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении). В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность). wikipedia.green Значение словосочетания «сила тока». Обозначение сила тока
Действующее значение силы тока обозначение. Действующие значения силы тока и напряжения
 а) б)
а) б)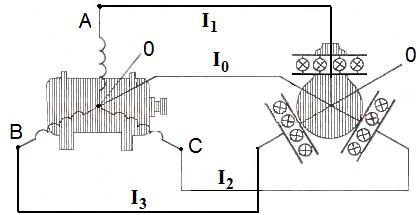
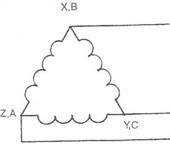 Рисунок 3.6. Пример соединения треугольником
Рисунок 3.6. Пример соединения треугольником за время
за время , определяется по формуле
, определяется по формуле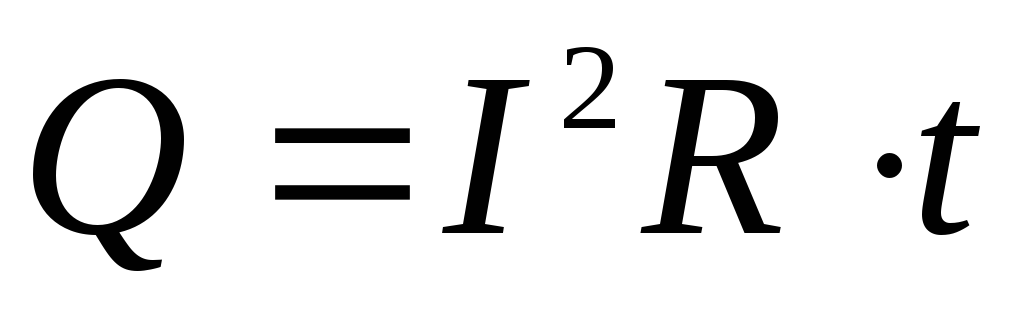 . Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени . Поделим период колебаний
. Поделим период колебаний на очень большое число малых промежутков времени
на очень большое число малых промежутков времени . Количество теплоты
. Количество теплоты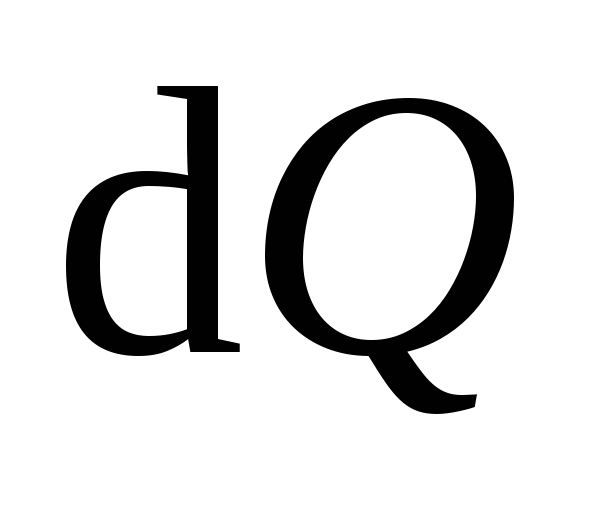 , выделяемое на сопротивлении
, выделяемое на сопротивлении за время
за время :
: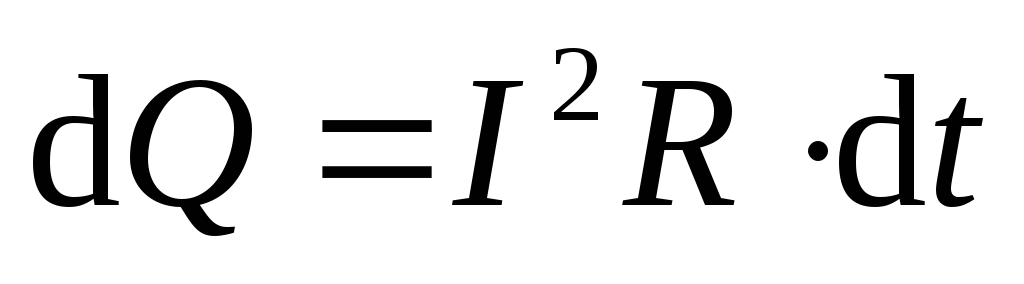 . Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием: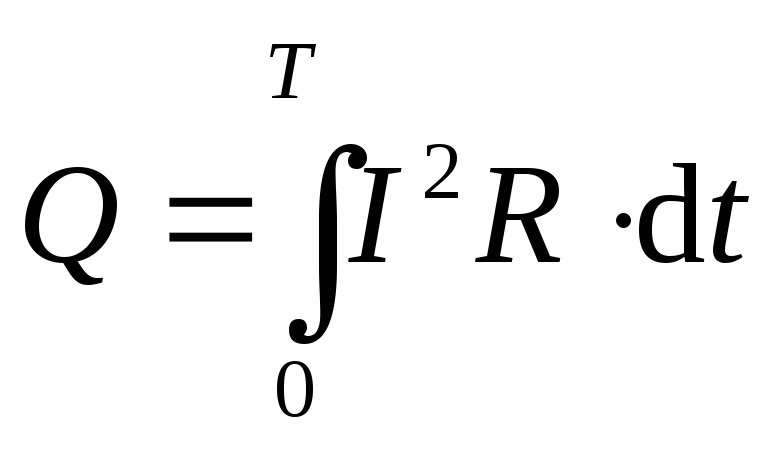 .
. ,
,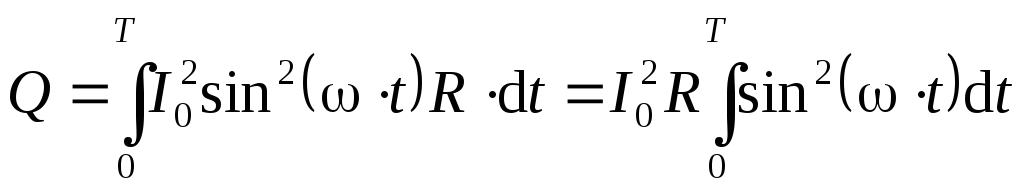 .
.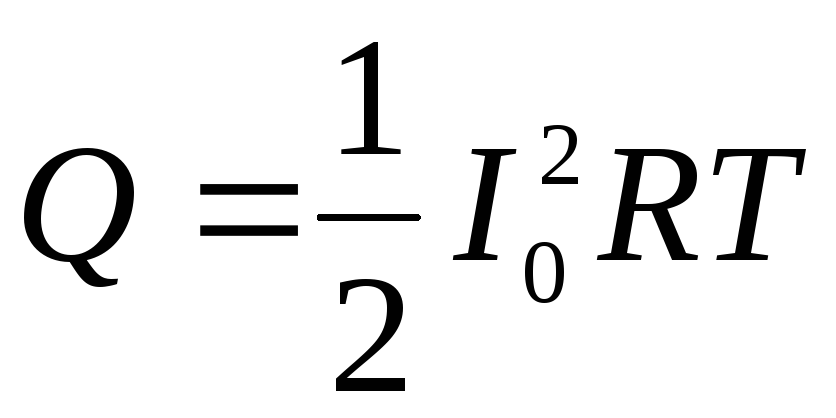 .
. , то за время, равное
, то за время, равное , выделилось бы тепло
, выделилось бы тепло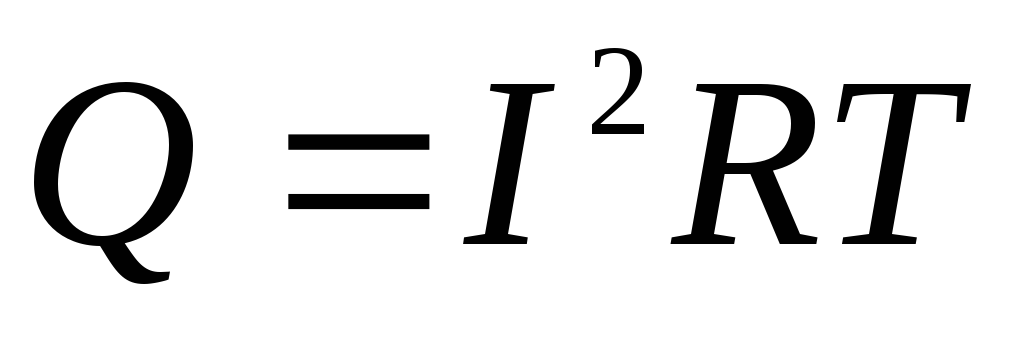 . По определению постоянный ток
. По определению постоянный ток , оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока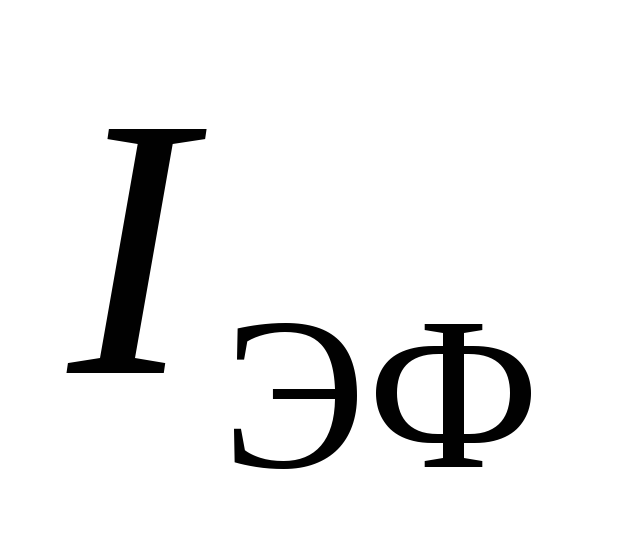 . Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов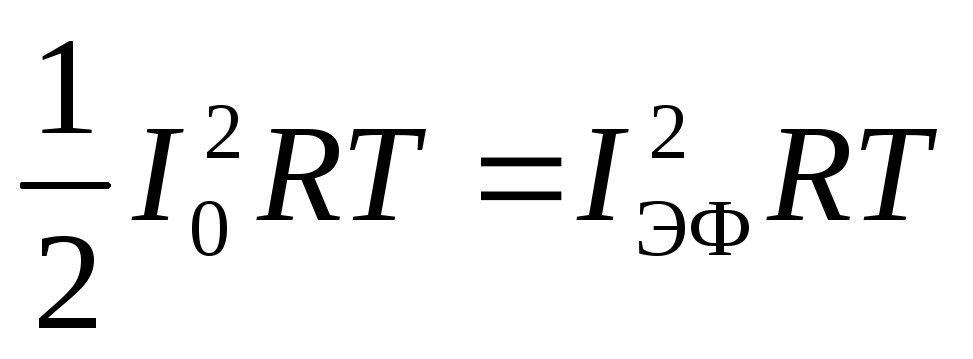

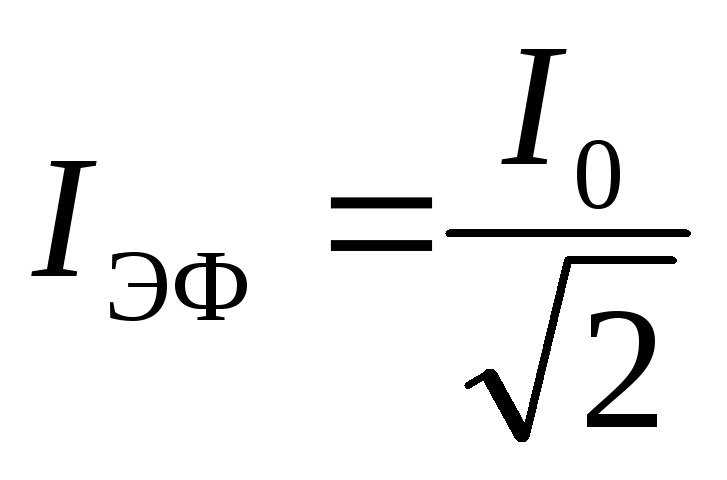 (4.28)
(4.28)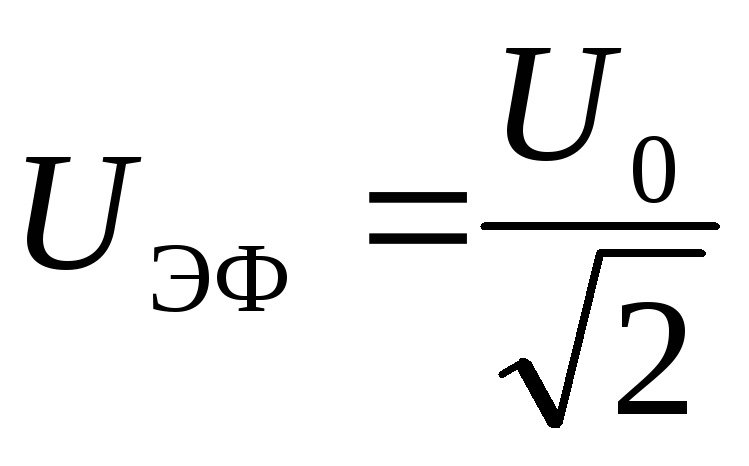 (4.29)
(4.29)4.4.5. Мощность в цепи переменного тока
 , т.е. сила тока и напряжение изменяются по законам:
, т.е. сила тока и напряжение изменяются по законам: ,
,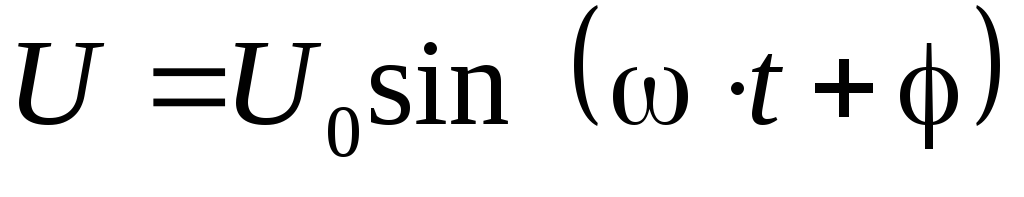 .
.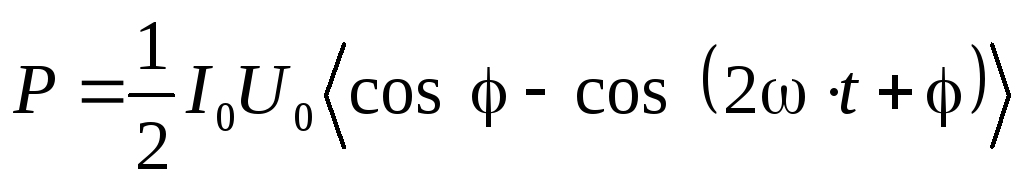 .
.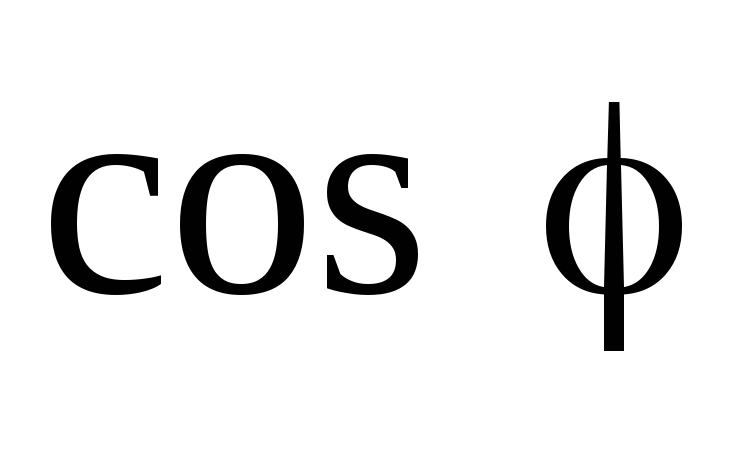 усреднять не нужно, так как она не зависит от времени, следовательно:
усреднять не нужно, так как она не зависит от времени, следовательно: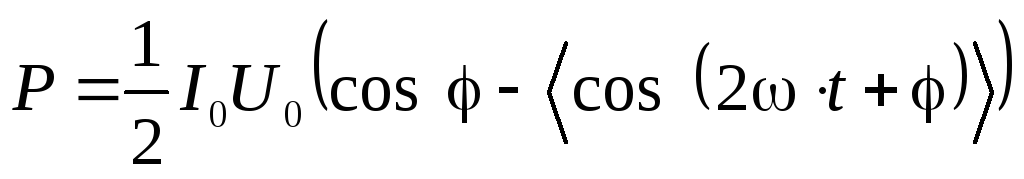 .
.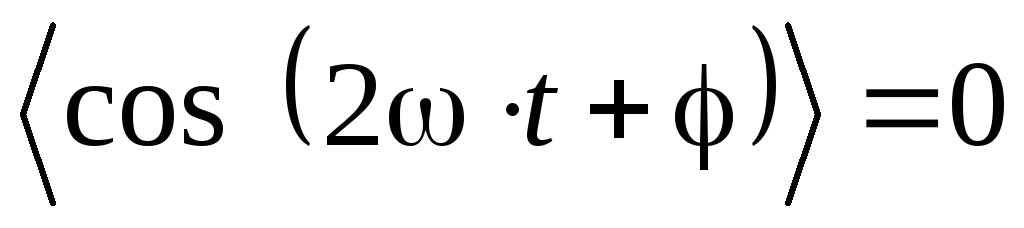 , поэтому
, поэтому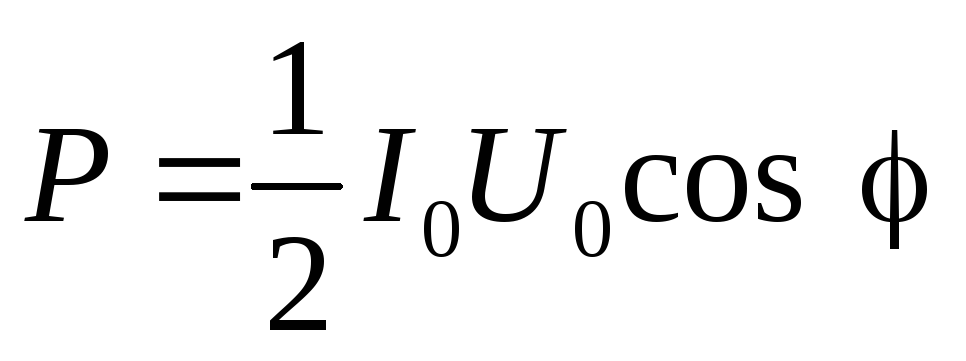 (4.30)
(4.30)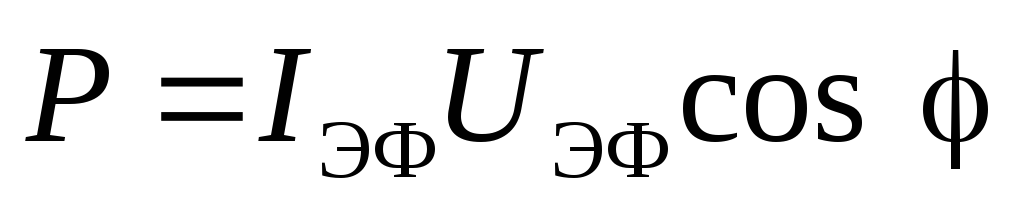 . (4.31)
. (4.31)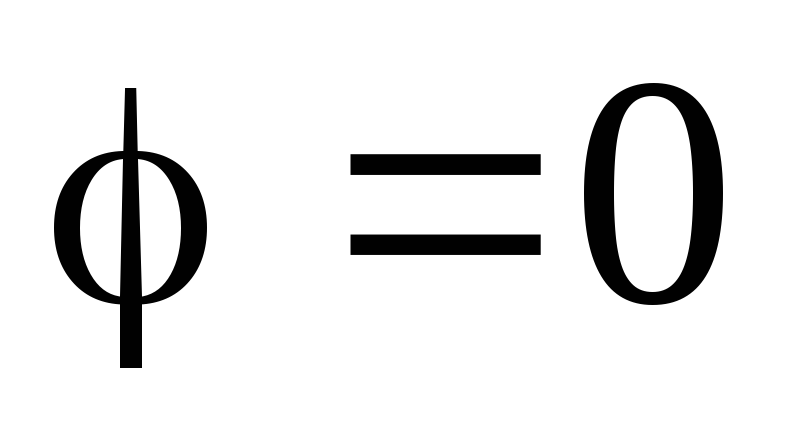 и
и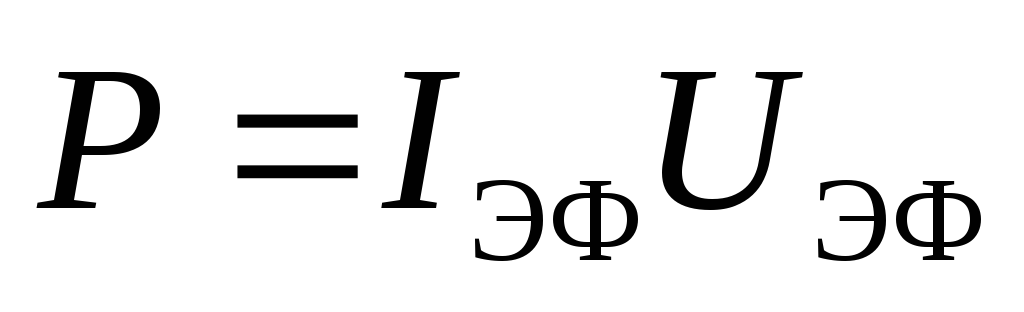 . Если участок цепи содержит только индуктивность или только ёмкость, то
. Если участок цепи содержит только индуктивность или только ёмкость, то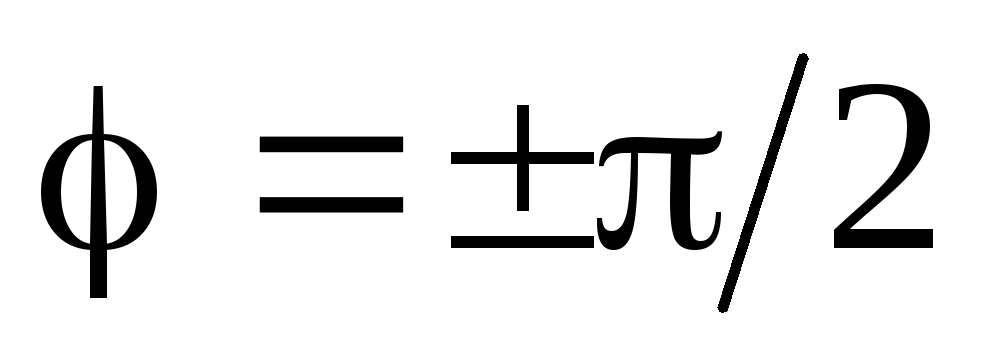 и
и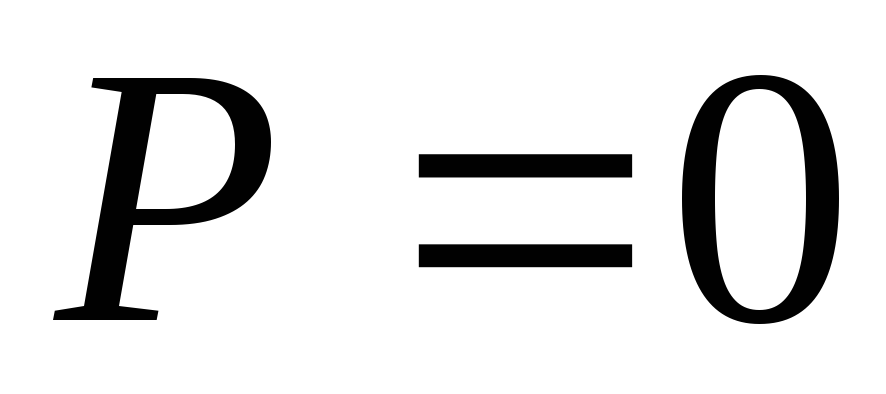 .
. при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.
при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается. может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).
может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27). . Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением
. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением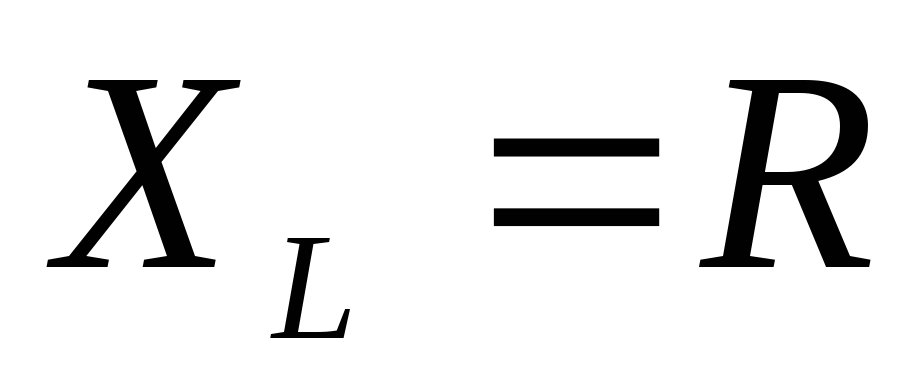 а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.
а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь. , расходуемая мощность
, расходуемая мощность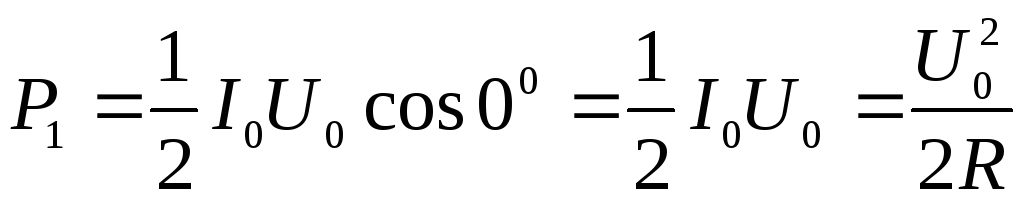 (см. формулу (4.30)).
(см. формулу (4.30)).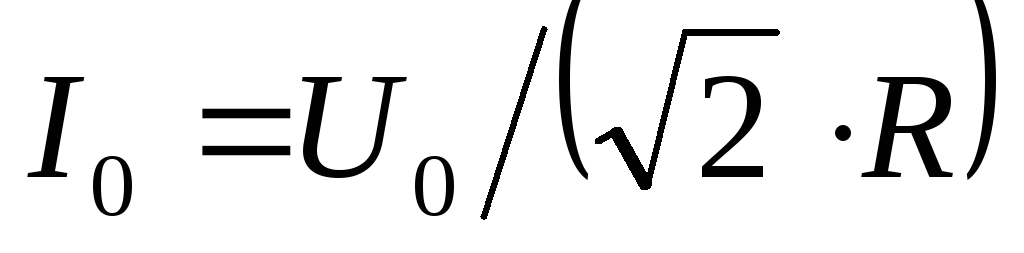 . Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора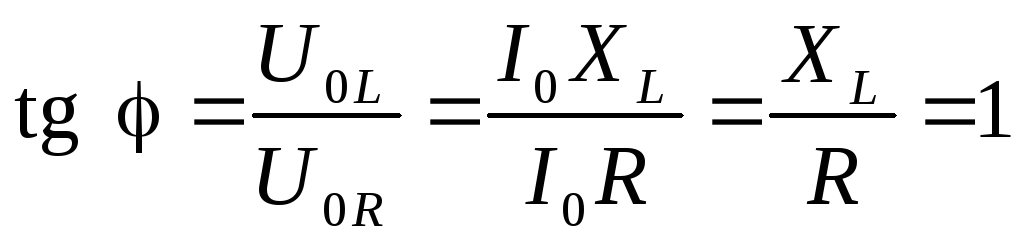

 .
.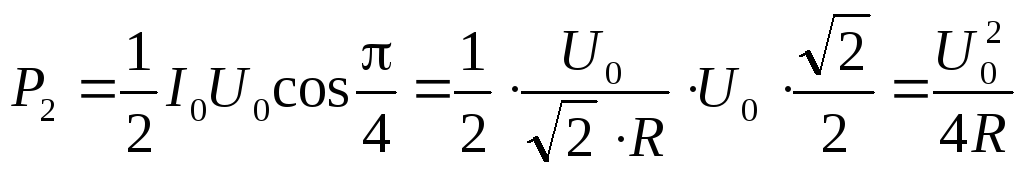 .
.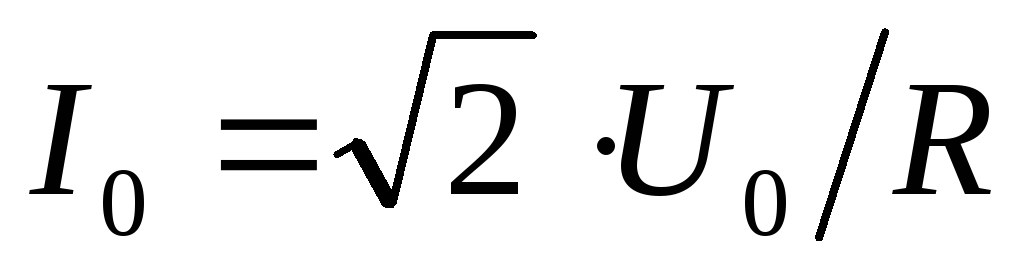 . Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора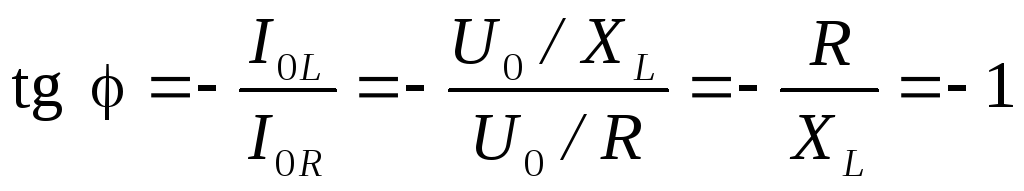

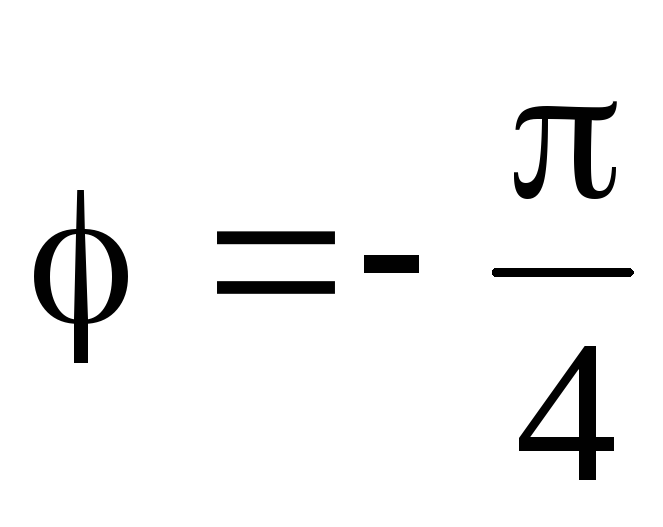 .
.Сила тока — Википедия
Примечания
Литература
1. Какая связь существует между напряжением, током и сопротивлением? | 2. Закон Ома | Часть1
1. Какая связь существует между напряжением, током и сопротивлением?
Какая связь существует между напряжением, током и сопротивлением?
Электрическая цепь считается сформированной тогда, когда создан такой проводящий путь, который позволяет свободным электронам непрерывно перемещаться. Это непрерывное движение свободных электронов по проводникам цепи называется током. Иногда его, по аналогии с потоком воды через трубу, называют "потоком".
Сила побуждающая электроны "течь" по цепи называется напряжением. Напряжение - это определённая мера потенциальной энергии, которая всегда взаимосвязана с двумя точками цепи. Когда мы говорим что в схеме присутствует определенная величина напряжения, мы имеем в виду величину потенциальной энергии, необходимой для перемещения электронов из одной точки цепи в другую. Без привязки к двум конкретным точкам цепи термин "напряжение" не имеет смысла.
При движении свободных электронов через проводники, определенное воздействие на них оказывает сила трения, которая препятствует движению. Это противодействие движению называется сопротивлением. Величина тока в цепи зависит от величины напряжения, заставляющего электроны двигаться, а так же от величины сопротивления, тормозящего поток электронов. Так же как и напряжение, сопротивление взаимосвязано с двумя точками цепи.
Чтобы конкретизировать понятия величины тока, напряжения и сопротивления, мы должны присвоить им единицы измерения, точно также, как единицы измерения присвоены массе, температуре, объему, длине и другим видам физических величин. Например, для массы мы используем единицу измерения "килограмм" или "грамм", для температуры - градус Фаренгейта или градус Цельсия. Стандартные единицы измерения силы тока, напряжения и сопротивления приведены в таблице:

"Обозначение" каждой величины - это буква латинского алфавита, которая используется для представления величины в алгебраическом уравнении. Использование латинских букв в физических и технических дисциплинах признано на международном уровне. "Аббревиатура" представляет собой первую букву единицы измерения на русском и английском языках. Исключение составляет аббревиатура слова Ом, которую в английской версии представляет буква греческого алфавита.
Каждая единица измерения названа в честь известного экспериментатора в области электроники: Ампер - в честь француза Ампера Андре Мари, Вольт - в честь итальянца Алессандро Вольта, Ом - в честь немца Ома Георга Симона.
Обозначение каждой величины имеет определенный смысл. Буква "R" (resistance) для сопротивления говорит сама за себя. Напряжение в нашей стране обозначается буквой "U", а за границей оно обозначается буквой "V" (voltage), что тоже говори само за себя. Что касается буквы "I" для обозначения силы тока, и буквы "E" - для второго обозначения напряжения, то они немного не вписываются в это правило. "I", как многие полагают, означает "Intensity" (Интенсивность (потока электронов)), а "E" - "Electromotive force" (Электродвижущую силу). Обозначения "E" и "U" по большей части являются взаимозаменяемыми, однако, некоторые радиолюбители резервируют букву "E" для обозначения напряжения источника питания (батареи, генератора и др.), а буквой "U" обозначают напряжение чего-нибудь еще.
Все эти обозначения используют заглавные буквы, кроме случаев, когда величина (особенно напряжения или тока) описывается в пределах короткого промежутка времени (так называемое "мгновенное" значение). Например, стабильное на протяжении длительного периода времени напряжение батареи обозначается заглавной буквой "E", а пиковое напряжение в момент удара молнии в линию электропередач скорее всего будет обозначено строчной буквой "e" (или "u"). Это же правило применяется и к силе тока, где строчная буква "i" обозначает силу тока в определенный момент времени. Большинство измерений постоянного тока (DC) обозначается заглавными буквами, потому что он стабилен с течением времени.
Одной из основополагающих, но редко используемых единиц измерения в электронике является кулон. Кулон это мера электрического заряда, он пропорционален количеству свободных электронов. Один кулон равен 6,250,000,000,000,000,000 электронов. Величина электрического заряда обозначается буквой "Q", а аббревиатура кулона - буква "C" (coulomb). 1 Амер (единица измерения потока электронов) равен 1 Кулону электронов, проходящих через определенную точку цепи за 1 секунду времени. Иными словами, электрический ток - это скорость движения электрического заряда через проводник.
Как было сказано выше, напряжение - это количество потенциальной энергии на единицу электрического заряда, необходимой для перемещения электронов из одной точки цепи в другую. Поэтому, прежде чем мы сможем точно определить что из себя представляет "Вольт", мы должны понять, как измерить величину называемую "потенциальной энергией". Общей единицей измерения для любой энергии является джоуль. Джоуль равен работе, совершаемой при перемещении точки приложения силы, равной одному ньютону, на расстояние одного метра в направлении действия силы. Исходя из вышеприведенного определения напряжения, 1 Вольт равен 1 Джоулю электрической потенциальной энергии на (деленному на) 1 Кулон заряда. Таким образом, 9-вольтовая батарея затрачивает 9 джоулей энергии на перемещение каждого кулона электронов через цепь.
Рассмотренные обозначения и единицы измерения электрических величин очень важно знать, так как мы, с настоящего момента, начинаем исследовать соотношения между ними в электрических цепях. Первым, и возможно самым важным соотношением между током, напряжением и сопротивлением является закон Ома, открытый и опубликованный Георгом Симоном Омом в 1827 году. Основным открытием Ома было то, что сила тока в проводнике прямопропорциональна напряжению, приложенному к его концам. Ом выразил своё открытие в виде простого уравнения, описывающего взаимосвязь тока, напряжения и сопротивления:

В этом алгебраическом выражении сила тока (I) прямопропорциональна напряжению (U) и обратно пропорциональна сопротивлению (R). Используя формулу закона Ома и методы алгебры, можно вычислить напряжение и сопротивление:

Давайте посмотрим, как эти уравнения работают при анализе простых электрических схем:

В приведенной выше схеме есть только один источник напряжения (батарея слева) и одно сопротивление току (лампа справа). Это делает ее очень простой в применении закона Ома. Если нам известны значения любых двух из трех величин (силы тока, напряжения и сопротивления) в этой схеме, то используя закон Ома, мы можем вычислить третью.
В первом примере мы вычислим силу тока (I) при заданных значениях напряжения (U) и сопротивления (R):

Чему равна сила тока (I) в этой схеме?

Во втором примере мы вычислим сопротивление (R) при заданных значениях напряжения (U) и силы тока (I):

Чему равно сопротивление (R) лампы?

В последнем примере мы вычислим величину поставляемого батареей напряжения (U) при заданных значениях силы тока (I) и сопротивления (R):

Чему равно поставляемое батареей напряжение (U)?

Закон Ома очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при обучении электронике, что намертво врезается в память серьезных студентов. Для тех-же, кто не дружит с алгеброй, существует небольшая уловка для запоминания этого закона. Единственное что нужно сделать, это заключить буквы U, I и R в треугольник следующим образом:

Если вам известны значения U и I, и нужно вычислить R, то просто зачеркните эту букву в треугольнике, и вы увидите что нужно сделать:

Аналогичным образом можно вычислить значения I и U:


Краткий обзор:
-
Напряжение измеряется в вольтах, и обозначается буквами "E" или "U".
-
Сила тока измеряется в амперах, и обозначается буквой "I".
-
Сопротивление измеряется в омах, и обозначается буквой "R".
-
Закон Ома: I = E/R ; U = IR ; R = E/I.
www.radiomexanik.spb.ru
Сила тока Википедия
Сила тока — физическая величина I{\displaystyle I}, равная отношению количества заряда ΔQ{\displaystyle \Delta Q}, прошедшего через некоторую поверхность за время Δt{\displaystyle \Delta t}, к величине этого промежутка времени[1]:
I=ΔQΔt.{\displaystyle I={\frac {\Delta Q}{\Delta t}}.}В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.
Обычно обозначается символом I{\displaystyle I}, от фр. intensité du courant.
Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ. 1 А = 1 Кл/с.
По закону Ома сила тока I{\displaystyle I} для участка цепи прямо пропорциональна приложенному напряжению U{\displaystyle U} к участку цепи и обратно пропорциональна сопротивлению R{\displaystyle R} проводника этого участка цепи:
I=UR.{\displaystyle I={\frac {U}{R}}.}По закону Ома для полной цепи
I=εR+r{\displaystyle I={\frac {\varepsilon }{R+r}}}Носителями заряда, движение которых приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступают электроны, ионы или дырки. Сила тока зависит от заряда q{\displaystyle q} этих частиц, их концентрации n{\displaystyle n}, средней скорости упорядоченного движения частиц vcp→{\displaystyle {\vec {v_{cp}}}}, а также площади S{\displaystyle S} и формы поверхности, через которую течёт ток.
Если n{\displaystyle n} и vcp→{\displaystyle {\vec {v_{cp}}}} постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде
I=qnvcpcosαS,{\displaystyle I=qnv_{cp}\cos \alpha S,}где α{\displaystyle \alpha } — угол между скоростью частиц и вектором нормали к поверхности.
В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока dI{\displaystyle dI}, протекающего через малый элемент поверхности площадью dS{\displaystyle dS}:
dI=qnvcpcosαdS.{\displaystyle dI=qnv_{cp}\cos \alpha dS.}Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности
I=∫SqnvcpcosαdS.{\displaystyle I=\int \limits _{S}qnv_{cp}\cos \alpha dS.}В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид
I=∫SenvcpcosαdS.{\displaystyle I=\int \limits _{S}env_{cp}\cos \alpha dS.}где e{\displaystyle e} — элементарный электрический заряд.
Вектор qnvcp→{\displaystyle qn{\vec {v_{cp}}}} называют плотностью электрического тока. Как следует из сказанного выше, его величина равна силе тока, протекающей через малый элемент поверхности единичной площади, расположенный перпендикулярно скорости vcp→{\displaystyle {\vec {v_{cp}}}}, а направление совпадает с направлением упорядоченного движения заряженных частиц[2].
Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).
В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).
Примечания
Литература
wikiredia.ru
Сила тока. Амперметр — урок. Физика, 8 класс.
В процессе своего движения вдоль проводника заряженные частицы (в металлах это электроны) переносят некоторый заряд. Чем больше заряженных частиц, чем быстрее они движутся, тем больший заряд будет ими перенесён за одно и то же время. Электрический заряд, проходящий через поперечное сечение проводника за 1 секунду, определяет силу тока в цепи.Сила тока \((I)\) — скалярная величина, равная отношению заряда (\(q\)), прошедшего через поперечное сечение проводника, к промежутку времени (\(t\)), в течение которого шёл ток.
I=qt, где \(I\) — сила тока, \(q\) — заряд, \(t\) — время.
Единица измерения силы тока в системе СИ — \([I] = 1 A\) (ампер).
В 1948 г. было предложено в основу определения единицы силы тока положить явление взаимодействия двух проводников с током:
при прохождении тока по двум параллельным проводникам в одном направлении проводники притягиваются, а при прохождении тока по этим же проводникам в противоположных направлениях — отталкиваются.


За единицу силы тока \(1 A\) принимают силу тока, при которой два параллельных проводника длиной \(1\) м, расположенные на расстоянии \(1\) м друг от друга в вакууме, взаимодействуют с силой \(0,0000002\)\(H\).
Единица силы тока называется ампером (\(A\)) в честь французского учёного А.М. Ампера.
 |
Андре-Мари Ампер (1775 - 1836) |
А.М. Ампер ввёл такие термины, как электростатика, электродинамика, соленоид, ЭДС, напряжение, гальванометр, электрический ток и т.д.
Ампер — довольно большая сила тока. Например, в электрической сети квартиры через включённую \(100\) Вт лампочку накаливания проходит ток с силой, приблизительно равной \(0,5A\). Ток в электрическом обогревателе может достигать \(10A\), а для работы карманного микрокалькулятора достаточно \(0,001A\).Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например, миллиампер (мА) и микроампер (мкА):\(1 мA = 0,001 A\), \(1 мкA = 0,000001 A\), \(1 кA =1000 A\).То есть \(1 A = 1000 мA\), \(1 A = 1000000 мкA\), \(1 A = 0,001 кA\).
Если электроны перемещаются в одном направлении, т.е. — от одного полюса источника тока к другому, то такой ток называют постоянным.Переменным называется ток, сила и направление которого периодически изменяются.
В бытовых электросетях используют переменный ток напряжением \(220\) В и частотой \(50\) Гц. Это означает, что ток за \(1\) секунду \(50\) раз движется в одном направлении и \(50\) раз — в другом. У источников переменного тока нет полюсов. У многих приборов имеется блок питания, который преобразует переменный ток в постоянный (у телевизора, компьютера и т.д.).
Силу тока измеряют амперметром. В электрической цепи он обозначается так:

Обрати внимание!
Амперметр включают в цепь последовательно с тем прибором, силу тока в котором нужно измерить. Амперметр нельзя подсоединять к источнику тока, если в цепь не подключён потребитель!
Измеряемая сила тока не должна превышать максимально допустимую силу тока для измерения амперметром. Поэтому существуют различные амперметры.
 |  |
Микроамперметр | Миллиамперметр |
 |  |
Амперметр | Килоамперметр |
Обрати внимание!
Различают амперметры для измерения силы постоянного тока и силы переменного тока.
Их можно различить по обозначениям:
- «~» означает, что амперметр предназначен для измерения силы переменного тока;
- «—» означает, что амперметр предназначен для измерения силы постоянного тока.
Можно обратить внимание на клеммы прибора. Если указана полярность («\(+\)» и «\(-\)»), то это прибор для измерения постоянного тока.
Иногда используют буквы \(AC/DC\). В переводе с английского \(AC\) (alternating current) — переменный ток, а \(DC\) (direct current) — постоянный ток.
Для измерения силы постоянного тока | Для измерения силы переменного тока |
 |  |
 |
Для измерения силы тока можно использовать и мультиметр. Перед измерением необходимо прочитать инструкцию, чтобы правильно подключить прибор.

Обрати внимание!
Включая амперметр в цепь постоянного тока, необходимо соблюдать полярность (см. рисунок): провод, который идёт от положительного полюса источника тока, нужно соединять с клеммой амперметра со знаком «+»; провод, который идёт от отрицательного полюса источника тока, нужно соединять с клеммой амперметра со знаком «-».
Если полярность на источнике тока не указана, следует помнить, что длинная линия соответствует плюсу, а короткая — минусу.

В цепь переменного тока включается амперметр для измерения переменного тока. Он полярности не имеет.

Обрати внимание!
В цепи, состоящей из источника тока и ряда проводников, соединённых так, что конец одного проводника соединяется с началом другого, сила тока во всех участках одинакова.
Это видно из опыта, изображённого на рисунке.

Обрати внимание!
Безопасным для организма человека можно считать переменный ток силой не выше \(0,05 A\), ток силой более \(0,05 — 0,1 A\) опасен и может вызвать смертельный исход.
Источники:
Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.
http://class-fizika.narod.ru/8_28.htm http://school.xvatit.com/index.php?title=%D0%A1%D0%B8%D0%BB%D0%B0_%D1%82%D0%BE%D0%BA%D0%B0http://physics.kgsu.ru/index.php?option=com_content&view=article&id=217&Itemid=72
http://kamenskih3.narod.ru/untitled74.htm
www.yaklass.ru
Значение словосочетания СИЛА ТОКА. Что такое СИЛА ТОКА?
Сила тока — физическая величина
I
{\displaystyle I}
, равная отношению количества заряда
Δ
Q
{\displaystyle \Delta Q}
, прошедшего через некоторую поверхность за время
Δ
t
{\displaystyle \Delta t}
, к величине этого промежутка времени:
I
=
Δ
Q
Δ
t
.
{\displaystyle I={\frac {\Delta Q}{\Delta t}}.}
В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.
Обычно обозначается символом
I
{\displaystyle I}
, от фр. intensité du courant.
Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ. 1 А = 1 Кл/с.
По закону Ома сила тока
I
{\displaystyle I}
для участка цепи прямо пропорциональна приложенному напряжению
U
{\displaystyle U}
к участку цепи и обратно пропорциональна сопротивлению
R
{\displaystyle R}
проводника этого участка цепи:
I
=
U
R
.
{\displaystyle I={\frac {U}{R}}.}
По закону Ома для полной цепи
I
=
ε
R
+
r
{\displaystyle I={\frac {\varepsilon }{R+r}}}
Носителями заряда, движение которых приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступают электроны, ионы или дырки. Сила тока зависит от заряда
q
{\displaystyle q}
этих частиц, их концентрации
n
{\displaystyle n}
, средней скорости упорядоченного движения частиц
v
c
p
→
{\displaystyle {\vec {v_{cp}}}}
, а также площади
S
{\displaystyle S}
и формы поверхности, через которую течёт ток.
Если
n
{\displaystyle n}
и
v
c
p
→
{\displaystyle {\vec {v_{cp}}}}
постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде
I
=
q
n
v
c
p
cos
α
S
,
{\displaystyle I=qnv_{cp}\cos \alpha S,}
где
α
{\displaystyle \alpha }
— угол между скоростью частиц и вектором нормали к поверхности.
В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока
d
I
{\displaystyle dI}
, протекающего через малый элемент поверхности площадью
d
S
{\displaystyle dS}
:
d
I
=
q
n
v
c
p
cos
α
d
S
.
{\displaystyle dI=qnv_{cp}\cos \alpha dS.}
Тогда выражение для силы тока, проте
kartaslov.ru
Что значит сила тока - Значения слов
Сила токаЭлектрическая мощность Электрическое сопротивление Сила тока — физическая величина I, равная отношению количества заряда ΔQ, прошедшего через некоторую поверхность за время Δt, к величине этого промежутка времени:
$I=\frac{\Delta Q}{\Delta t}.$
В качестве рассматриваемой поверхности часто используется поперечное сечение проводника .
Обычно обозначается символом I, от .
Сила тока в Международной системе единиц измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ . 1 А = 1 Кл / с .
По закону Ома сила тока I для участка цепи прямо пропорциональна приложенному напряжению U к участку цепи и обратно пропорциональна сопротивлению R проводника этого участка цепи:
$I = \frac{U}{R}.$По закону Ома для полной цепи
$I = \frac{\varepsilon}{R+r}$
Носителями заряда, движение которых приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступают электроны , ионы или дырки . Сила тока зависит от заряда q этих частиц, их концентрации n, средней скорости упорядоченного движения частиц $\vec {v_{cp}}$, а также площади S и формы поверхности, через которую течёт ток.
Если n и $\vec {v_{cp}}$ постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде
I = qnvcosαS,где α — угол между скоростью частиц и вектором нормали к поверхности.
В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока dI, протекающего через малый элемент поверхности площадью dS:
dI = qnvcosαdS.Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности
$I = \int \limits_S q n v_{cp} \cos \alpha dS.$В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид
$I = \int \limits_S e n v_{cp} \cos \alpha dS.$где e — элементарный электрический заряд .
Вектор $q n \vec {v_{cp}}$ называют плотностью электрического тока . Как следует из сказанного выше, его величина равна силе тока, протекающей через малый элемент поверхности единичной площади, расположенный перпендикулярно скорости $\vec {v_{cp}}$, а направление совпадает с направлением упорядоченного движения заряженных частиц.
Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр ). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический , электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).
В случае переменного тока различают мгновенную силу тока, амплитудную силу тока и эффективную силу тока .
xn--b1algemdcsb.xn--p1ai







Поделиться с друзьями: