Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его. Явление электромагнитной индукции было открыто М. Фарадеем. Опыты Фарадея Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении. Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле. Объяснения возникновения индукционного тока Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году. Свойства вихревого электрического поля: Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности): Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб). Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции: Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь. В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0. Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его). В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность. Закон электромагнитной индукции (закон Фарадея): ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром: Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока. Если контур состоит из \( N \) витков, то ЭДС индукции: Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \): При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна: где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \). Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы. Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника. Важно!Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам: Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Алгоритм решения задач с использованием правила Ленца: Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии. Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем. При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке. В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи. Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время. При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника. Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки. Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке. При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке. ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна: ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке. Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике. Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре: Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током: Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник. Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер: Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт. При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле: Алгоритм решения задач по теме «Электромагнитная индукция»: 1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур. 2. Записать формулу: 3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции. 4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики). 5. Решить полученную систему уравнений относительно искомой величины. 6. Решение проверить. Электромагнитная индукция fizi4ka.ru
Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10−10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм2. Какой максимальный заряд пройдет по кольцу при выключении поля?
Решение. Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля. Поток индукции магнитного поля через площадь кольца определяется формулами: Ф1 = B
1S cos α, где B
1 — первоначальное значение модуля индукции магнитного поля, B
1 = 250 мТл; S — площадь кольца; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца; Ф2 = B
2S cos α = 0, где B
2 — значение модуля индукции после выключения магнитного поля, B
2 = 0. Изменение потока вектора индукции магнитного поля определяется разностью ∆Ф = Ф2 − Ф1 = −Ф1, или, с учетом явного вида Ф1, ∆Ф = −B
1S cos α. Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,
|ℰi|=|ΔФΔt|=|−B1ScosαΔt|=B1S|cosα|Δt, где ∆t — интервал времени, за который происходит выключение поля. Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:
Ii=|ℰi|R=B1S|cosα|RΔt, где R — сопротивление кольца. При протекании индукционного тока по кольцу переносится индукционный заряд
qi=IiΔt=B1S|cosα|R. Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):
qimax=IiΔt=B1SR. Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля. Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление. Площадь кольца — площадь круга радиусом r, периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:
l = 2πr, где l — длина проволоки, l = 1,57 м. Отсюда следует, что радиус кольца определяется отношением
r=l2π, а его площадь —
S=πr2=πl24π2=l24π. Сопротивление кольца задается формулой
R=ρlS0, где ρ — удельное сопротивление материала проволоки, ρ = 50,0 × × 10−10 Ом ⋅ м; S
0 — площадь поперечного сечения проволоки, S
0 = = 0,100 мм2. Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:
qimax=B1l2S04πρl=B1lS04πρ. Вычислим:
qimax=250⋅10−3⋅1,57⋅0,100⋅10−64⋅3,14⋅50,0⋅10−10=0,625 Кл=625 мКл. При выключении поля по кольцу проходит заряд, равный 625 мКл. vedy.by В нашем мире все виды существующих сил, за исключением сил тяготения, представлены электромагнитными взаимодействиями. Во Вселенной, несмотря на удивительное разнообразие воздействий тел друг на друга, в любых веществах, живых организмах всегда встречается проявление электромагнитных сил. Как произошло открытие электромагнитной индукции (ЭИ), расскажем ниже. ... Вконтакте Facebook Twitter Google+ Мой мир Так нельзя ли добиться его возникновения посредством магнитного поля — подобную задачу поставил Майкл Фарадей. В 1821 году он отметил это свойство в своем дневнике о превращении магнетизма в электричество. Успех к ученому пришел не сразу. Лишь глубокая уверенность в единстве природных сил и упорный труд привели его через десять лет к новому великому открытию. Решение задачи долго не давалось Фарадею и другим его коллегам, потому как они пытались получить электричество в неподвижной катушке, используя действие постоянного магнитного поля. Между тем, впоследствии выяснилось: изменяется количество силовых линий, пронизывающих провода, и возникает электроэнергия. Процесс появления в катушке электричества в результате изменения магнитного поля характерен для электромагнитной индукции и определяет это понятие. Вполне закономерно, что разновидность тока, возникающего в ходе данного процесса, называется индукционным. Эффект сохранится, если саму катушку оставить без движения, но перемещать при этом магнит. С использованием второй катушки можно и вовсе обойтись без магнита. Если пропустить электричество через одну из катушек, то при их взаимном перемещении во второй возникнет индукционный ток. Можно надеть одну катушку на другую и менять величину напряжения одной из них, замыкая и размыкая ключ. При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй. Во время опытов легко обнаружить, что увеличивается число пронизывающих катушку силовых линий — стрелка используемого прибора (гальванометр) смещается в одну сторону, уменьшается – в иную. Более тщательное исследование показывает, что сила индукционного тока прямо пропорциональна скорости изменения числа силовых линий. В этом заключен основной закон электромагнитной индукции. Данный закон выражает формула: Она применяется, если за период времени t магнитный поток изменяется на одну и ту же величину, когда скорость изменения магнитного потока Ф/t постоянна. Важно! Для индукционных токов справедлив закон Ома: I=/R, где — это ЭДС индукции, которую находят по закону ЭИ. Замечательные опыты, проведенные когда-то знаменитым английским физиком и ставшие основой открытого им закона, сегодня без особого труда способен проделать любой школьник. Для этих целей используются: Поворачивая, наклоняя и перемещая ее вверх и вниз, мы меняем число силовых линий магнитного поля, пронизывающих ее витки. Гальванометр регистрирует возникновение электричества с постоянно меняющимися в ходе опыта величиной и направлением. Находящиеся же относительно друг друга в покое катушка и магнит не создадут условий и для возникновения электричества. На основе проведенных исследований были сформированы еще два одноименных закона: Из всех существующих видов индукции огромное значение имеет обособленный вид данного явления – самоиндукция. Если мы возьмем катушку, которая имеет большое количество витков, то при замыкании цепи, лампочка загорается не сразу. На этот процесс может уйти несколько секунд. Очень удивительный на первый взгляд факт. Чтобы понять, в чем здесь дело, необходимо разобраться, что же происходит в момент замыкания цепи. Замкнутая цепь словно «пробуждает» электроток, начинающий свое движение по виткам провода. Одновременно в пространстве вокруг нее мгновенно создается усиливающееся магнитное поле. Катушечные витки оказываются пронизанными изменяющимся электромагнитным полем, концентрирующимся сердечником. Возбуждаемый же в витках катушки индукционный ток при нарастании магнитного поля (в момент замыкания цепи) противодействует основному. Мгновенное достижение им своего максимального значения в момент замыкания цепи невозможно, оно «растет» постепенно. Вот и объяснение, почему лампочка не вспыхивает сразу. Когда цепь размыкается, основной ток усиливается индукционным в результате явления самоиндукции, и лампочка ярко вспыхивает. Важно! Суть явления, названного самоиндукцией, характеризуется зависимостью изменения, возбуждающего индукционный ток электромагнитного поля от изменения силы текущего по цепи электротока. Направление тока самоиндукции определяет правило Ленца. Самоиндукция легко сравнима с инерцией в области механики, поскольку оба явления обладают схожими характеристиками. И действительно, в результате инерции под влиянием силы тело приобретает определенную скорость постепенно, а не сиюминутно. Не сразу – под действием самоиндукции — при включении батареи в цепь появляется и электричество. Продолжая сравнение со скоростью, заметим, он так же не способен мгновенно исчезнуть. Специалисты знают, что металлические трансформаторные сердечники, якоря генераторов и электродвигателей никогда не бывают сплошными. При их изготовлении на отдельные тонкие листы, из которых они состоят, накладывается слой лака, изолирующий один лист от другого. Нетрудно понять, какая сила заставляет человека создавать именно такое устройство. Под действием электромагнитной индукции в переменном магнитном поле сердечник пронизывают силовые линии вихревого электрополя. Представим, что сердечник изготовлен из сплошного металла. Поскольку его электрическое сопротивление невелико, возникновение индукционного напряжения большой величины было бы вполне объяснимым. Сердечник бы в итоге разогревался, и немалая часть электрической энергии терялась бесполезно. Кроме того, возникла бы необходимость принятия специальных мер для охлаждения. А изолирующие слои не позволяют достигать больших величин. Индукционные токи, присущие массивным проводникам, называются вихревыми не случайно – их линии замкнуты подобно силовым линиям электрополя, где они и возникают. Чаще всего вихревые токи применяются в работе индукционных металлургических печей для выплавки металлов. Взаимодействуя с породившим их магнитным полем, они иногда становятся причиной занимательных явлений. Возьмем мощный электромагнит и поместим между вертикально расположенными его полюсами, к примеру, пятикопеечную монету. Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды. Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды. Передвижение монеты напоминает перемещение тела в вязкой среде. Почему такое происходит. По правилу Ленца направления возникающих при передвижении монеты вихревых токов в неоднородном магнитном поле таковы, что поле магнита выталкивает монету вверх. Эту особенность используют для «успокоения» стрелки в измерительных приборах. Алюминиевая пластина, находящаяся между магнитными полюсами, прикрепляется к стрелке, и вихревые токи, возникающие в ней, способствуют быстрому затуханию колебаний. Демонстрацию явления электромагнитной индукции поразительной красоты предложил профессор Московского университета В.К. Аркадьев. Возьмем свинцовую чашу, обладающую сверхпроводящей способностью, и попробуем уронить над ней магнит. Он не упадет, а будет словно «парить» над чашей. Объяснение здесь простое: равное нулю электрическое сопротивление сверхпроводника способствует возникновению в нем электричества большой величины, способных сохраняться продолжительное время и «удерживать» магнит над чашей. По правилу Ленца, направление магнитного поля их таково, что отталкивает магнит и не дает ему упасть. Изучаем физику — закон электро-магнитной индукции Правильна формулировка закона Фарадея Электромагнитные силы – это силы, которые позволяют людям видеть окружающий мир и чаще других встречаются в природе, например, свет — тоже пример электромагнитных явлений. Жизнь человечества невозможно представить без данного явления. uchim.guru 01. Электромагнитная индукция – это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Фарадеем в 1831 г. Для демонстрации этого явления возьмем неподвижный магнит и проволочную катушка, концы которой соединим с гальванометром. Если катушку приблизить к одному из полюсов магнита, то во время движения стрелка гальванометра отклоняется – в катушке возбуждается электрический ток. При движении катушки в обратном направлении направление тока меняется на противоположное. То же самое происходит, если повернуть магнит на 180 градусов, не меняя направления движения катушки. Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающий при движении проводника. Рассмотрим случай, когда два параллельных провода АВ и CD замкнуты, справа – разомкнуты. Вдоль проводов может свободно скользить проводящий мостик BC. Когда мостик движется вправо со скоростью v, вместе с ним движутся электроны и положительные ионы. На каждый движущий заряд в магнитном поле действует сила Лоренца . На положительные ион она действует вниз, на отрицательные вверх. В результате электроны начнут перемещаться по мостику вверх, т.е. по нему потечет электрический ток, направленный вниз. Перераспределившись заряды создадут электрическое поле, которое возбудит токи и в остальных участках контураABCD. Сила Лоренца F в опыте играет роль сторонней силы, возбуждающей электрический ток. 02. Электродвижущая сила индукции (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока. Знак минус поставлен потому, что стороннее поле направлено против положительного обхода контура. Величина lv есть приращение площади контура ABCD в единицу времени, или скорость приращении этой площади. Поэтому равна Основной закон электромагнитной индукции.(Дифференциальная форма закона электромагнитной индукции) При движении замкнутого провода в магнитном поле в нем возбуждается электродвижущая сила, пропорциональная скорости приращения магнитного потока, пронизывающего контур провода. 03. Правило Ленца (принцип Ле Шателье) Индукционный ток всегда имеет такой направление, что он ослабляет действие причины, возбуждающий этот ток. Возьмем в магнитном поле замкнутый проволочный виток, положительное направление обхода которого составляет с направлением поля правовинтовую систему. Допустим, что магнитный поток Ф возрастает. Тогда, согласно формуле , величинабудет отрицательна, а индукционный ток в витке потечет в отрицательном направлении. Такой ток, ослабляя внешнее магнитное поле, будет препятствовать возрастанию магнитного потока. Пусть теперь магнитный поток Ф убывает. Тогда величина станет положительной, а индукционный ток в витке потечет в положительном направлении и будет препятствовать убыванию магнитного поля и магнитного потока. 04. Индуктивность проводов. Рассмотрим тонкий замкнутый провод, по которому течет постоянный ток I. Внутри провода параллельно его оси проведем произвольный замкнутый математический контур s и установим на нем положительное направление. Если в пространстве нет ферримагнитных тел, то величина B(магнитное поле тока) и Ф(магнитный поток) будут пропорционально току. здесь - сила тока в гауссовской системе единиц, а- сила тока в системе СГСМ. - самоиндукция, или коэффициент самоиндукции провода. Он не зависит от силы тока, определяется только размерами и конфигурацией самого провода. Пример: Вычислим индуктивность соленоида. Пусть - длина соленоида,- общее число витков,- площадь одного витка. Индукция магнитного поля внутри соленоида Магнитный поток через один виток равен , я черезвитков -т.е. Получим индуктивность ( в сантиметрах) Магнитный поток - это поток Ф вектора магнитной индукции B через конечную поверхность S. За единицу магнитного потока принимают максвелл. Максвелл есть магнитный поток, создаваемый магнитным полем в один гаусс через перпендикулярную к нему площадь в один квадратный сантиметр. 05. Явления при замыкании тока Процесс замыкания Пусть цепь состоит из источника постоянного ЭДС, катушки самоиндукции и омического сопротивления. Полную индуктивность цепи обозначим через , а полное сопротивление– через . При замыкании ключа К ток не сразу достигает предельного значения, определяемого законом Ома, а нарастает постепенно. При этом возрастает также магнитный поток, пронизывающий контур цепи. Возникает электродвижущая сила индукции и соответствующий ей индукционный ток. Этот ток называют экстратоком замыкания. Согласно правилу Ленца направление экстратока замыкания противоположно направлению основного тока. Сила переменного тока не обязательно должна быть одной и той же на всех участках провода, так как в отдельных местах возможно накопление зарядов. Однако мы рассмотрим здесь только такие переменные токи, которые меняются во времени сравнительно медленно. Тогда мгновенные значения токов во всех участках неразветвленной цепи с высокой степенью точности одинаковы, а магнитный поля внутри проводов могут вычисляться по закону Био и Савара, как если бы токи были постоянными. Такие токи называются квазистационарными. Сила тока определяется выражением В практических единицах Дифференциальное уравнение для квазистационарных токов Если за время изменения тока провода не деформируются, то индуктивность , постоянна и может быть вынесена из-под знака производной При постоянном значении общее решение этого уравнения имеет вид Постоянная интегрирования C должна определяться из начального условия: в момент замыкания, т.е. при , то ток равен нулю. Используя это условие, находим. Эта формула применима в любой системе единиц. Где - постоянная, имеющая размерность времени: В гауссовской системе единиц: Полный ток I состоит из двух слагаемых, из которых второе, т.е. , определяет силу экстратока замыкания. Приэкстра ток стремится к нулю, а полный токI – к своему предельному значению . Таким образом, окончательное значение тока устанавливается постепенно. Быстроту установления определяется временем: по истечении временисила экстратока убывает враз. 06. Явления при размыкании тока Ключ К сначала замкнут. Направление токов показаны сплошными стрелками. Общий ток распределяется между параллельно включенными самоиндукцией и омическим сопротивлением. Если внутреннее сопротивление батареи пренебрежимо мало, то ток в катушке самоиндукции будет равен. После размыкания ключа К замкнутым останется только контур ABCD. Первоначальный ток, существовавший в катушке самоиндукции, обладал определенным запасом магнитной энергии, которая исчезает не сразу. Магнитное поле начнет убывать. Это возбудит электродвижущую силу и индукционный ток в контуре ABCD. Такой ток называется экстратоком размыкания. Экстраток показан пунктирными стрелками. В катушке самоиндукции экстраток течет в том же направлении , что и первоначальный ток, в остальных участках контура ABCD— в противоположном направлении. Если - общее сопротивление контура ABCD, то сила тока определится из дифференциального уравнения и начального условия: . Это дает, гдеопределяется прежним выражением. Электродвижущая сила индукции равна Если , то эта величина может значительно превзойти ЭДС батареи. В этом причина электрического пробоя, наблюдающегося иногда при выключении тока в цепях, содержащих большие индуктивности. Для демонстрации явления можно взять катушку длиной 50-60 см и диаметром 8-10 см сердечником из железных прутьев и обмоткой из нескольких слоев проволоки диаметром около 1 мм. Параллельно катушке присоединена лампочка. Лампочка рассчитана на напряжение, несколько превышающее ЭДС батареи. При замкнутой цепи лампочка горит тускло. При размыкании ключа К она ярко вспыхивает и даже может перегореть, так как ЭДС индукции превосходит в несколько раз ЭДС батареи. Рассмотрим теперь два витка (или две катушки), по которым текут постоянные токи и. Установим произвольно на этих витках положительные направления обхода. Если в окружающем пространстве нет ферромагнетиков, то магнитные потоки через виткиипропорциональны токам и могут быть представлены в виде Коэффициенты не зависят от токов, а определяются лишь формой, размерами и взаимным расположением витков. Они называются коэффициентами индуктивности. Если. Поэтомуесть индуктивность первого, а- второго витка. Оставшиеся два коэффициентаиназываются взаимными индуктивностями или коэффициентами взаимной индукции. 07. Энергия магнитного поля. Электрический ток обладает запасом энергии, называемой магнитной. Магнитная энергия может зависеть только от величины и распределения токов, а таксисе от магнитных свойств среды, заполняющей пространство. Рассмотрим сначала одиночный неподвижный замкнутый виток проволоки. Пусть в начальный момент сила тока в нем равна нулю. Будем каким-либо способом создавать и наращивать ток в витке . Тогда будет нарастать и магнитный поток через виток Ф. Возникнет электродвижущая сила индукции. Элементарная работа, которую должен совершить внешний источник против электродвижущей силы индукции, будет Полученное соотношение носит общий характер. Оно справедливо и для ферромагнитных материалов, так как при его выводе относительно магнитных свойств среды не вводилось никаких предположений. Однако если среда не обладает гистерезисом, в частности является пара- или диамагнитной, то работа пойдет только на увеличение магнитной энергии, так что Предположим, что ферромагнетики отсутствуют. Тогда причем для неподвижного провода самоиндукция L остается постоянной. Используя это и интегрируя, получим Для справедливости формулы несущественно, что во время нарастания тока виток оставался неподвижным, так как энергия зависит от состояния системы, но не от способа, каким было достигнуто это состояние Формула для произвольного числа витков. Предположим, что все витки неподвижны, будем увеличивать токи в них. Тогда для элементарной работы против электродвижущей силы индукции будет: Магнитная энергия в конечном состоянии представится интегралом: , где текущее значения соответствующих величин Для упрощения расчета будем наращивать все токи одновременно и притом так, чтобы они оставались пропорциональными друг другу. Таким образом, в любой момент будет соблюдаться соотношение - переменная величина, не зависящая отi. В начальном состоянии , в конечном. Так как при отсутствии ферромагнитных материалов магнитные потоки связаны с токами линейно, то для них справедливы такие же соотношения, т. е.. Таким образом или после интегрирования 08. Локализация магнитной энергии в пространстве. Выражение для магнитной энергии можно преобразовать в другую форму, которая соответствует иному представлению о месте нахождения энергии. Покажем это на примере длинного соленоида, по поверхности которого циркулирует ток с линейной плотностью . Пренебрегая краевыми эффектами, можно написать для поля Н внутри соленоида. ПустьS – площадь поперечного сечения соленоида. Тогда , получим Если - магнитная энергия, приходящаяся на единицу объема соленоида, то для ее дифференциала можно написать В случае пара- и диамагнитных сред и выражение можно проинтегрировать В общем случае постоянных электрических токов выражение для магнитной энергии можно преобразовать. Считая ток неподвижным и полагая в формуле , получим Вектор А и называется векторным потенциалом магнитного поля. Используя это соотношение и применяя теорему Стокса, находим Вместо линейного введем объемный элемент тока и воспользуемся теоремой о циркуляции 09. Основы теории Максвелла. Ток смещения. Основные уравнения электромагнитного поля в неподвижных средах, применимые не только к постоянным, но и к переменным электромагнитным полям, были установлены Максвеллом. К уравнениям Максвелла можно прийти путем последовательного обобщения опытных фактов.К основным уравнениям электродинамики присоединим закон сохранения электрического заряда. В дифференциальной форме он имеет вид Если электромагнитное поле стационарно, то уравнение переходит Теорема о циркуляции также может быть преобразована в дифференциальную форму Эти соотношения верны только для стационарных токов. Чтобы прийти к обобщенным уравнениям, воспользуемся следующим наводящим рассуждением. Поскольку дивергенция левой части уравнения тождественно равна нулю, в правой части этого уравнения должен стоять вектор, дивергенция которого также всегда равна нулю. В случае стационарных электромагнитных полей этот вектор должен переходить в j. Легко указать вектор, удовлетворяющий этим условиям. Дифференцируя по времени соотношениеполучаем - ток смещения Таким образом , т.е полный ток всегда соленоидален. Если в уравнении ток проводимостиj заменить полным током Для обобщения уравнений и В вакууме всякое изменение электрического поля во времени возбуждает в окружающем пространстве магнитное поле. 10. Система уравнений Максвелла. Система фундаментальных уравнений электродинамики В дифференциальной форме: теорема о циркуляции + ток смещения закон электромагнитной индукции теорема Гаусса в веществе теорема Гаусса для магнитного поля В Интегральной форме: Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами {электрическими токами), либо переменными электрическими полями. 11. Граничные условия. Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Можно, однако, достигнуть полной математической эквивалентности обеих форм уравнений Максвелла. Для этого надо дифференциальные уравнения дополнить граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Эти условия содержатся в интегральной форме уравнений Максвелла. Они были выведены в соответствующих местах курса и имеют вид Здесь - поверхностная плотность тока проводимости на рассматриваемой границе раздела, а i - поверхностная плотность тока проводимости на рассматриваемой границе раздела. В частном случае, когда поверхностных токов нет, последнее условие переходит в. 12. Материальные уравнения. Принципиальный способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электрической проводимости среды. В основе таких теорий лежат какие-то идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами Р, I, j, с одной стороны, и векторами Е и В — с другой. Таким путем, в зависимости от характера среды и электромагнитного поля, получаются более или менее сложные соотношения, которые и дополняют фундаментальные уравнения Максвелла до полной системы уравнений электродинамики. Наиболее просты материальные уравнения в случае слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных неферромагнитных и несегнетоэлектрических сред материальные уравнения могут быть записаны в виде , где - постоянные, характеризующие электромагнитные свойства среды. Они называются диэлектрической и магнитной проницаемостью и электрической проводимостью среды. Когда поля стационарны , уравнения Максвелла распадаются на две группы независимых уравнений. Первую группу составляют уравнения электростатики вторую — уравнения магнитостатики В этом случае электрическое и магнитное поля независимы друг от друга. Источниками электрического поля будут только электрические заряды, источниками магнитного поля — только токи проводимости. 13. Электромагнитные волны. электромагнитные волны, или возмущения, распространяющиеся в пространстве с определенной скоростью. Рассмотрим бесконечно протяженную однородную диэлектрическую среду с диэлектрической и магнитной проницаемостями и. Поместим в нее бесконечную равномерно заряженную плоскость, которую примем за координатную плоскость XY studfiles.net Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций. Эксперименты Фарадея Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени. Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит. Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца. Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности. Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине. Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока. ЭДС индукции Формула ЭДС индукции определена как: Е = — dФ/dt. Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью. Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев. Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула: Е = — В x l x v; Е = — В x l x v х sin α. Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам. Перемещение провода в МП Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков. ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S). Из формулы следует, что Ф подвержен изменениям в следующих случаях: В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС. Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени. Вращение контура в МП Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию. Для формулы ЭДС электромагнитной индукции применяется выражение: Е = В х ω х S x N x sin ωt, где: На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор). Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией. Поскольку МП пропорционально интенсивности тока, то: Ф = L x I, где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения. Для ЭДС индукции формула принимает вид: Е = — L x dI/dt. Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток. Взаимоиндукция Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда: М21 = (N2 x F21)/I1; Ф21 = (М21/N2) x I1; Е2 = — N2 x dФ21/dt = — M21x dI1/dt; Е1 = — M12 x dI2/dt; Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой. Взаимную индуктивность можно признать равной: М12 = М21 = М. Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К – коэффициент связи между двумя индуктивностями. Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот. Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания. elquanta.ru 1831 г. - М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, - появление, возникновение). Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или: явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром. Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы. Возникновение индукционного тока - следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: Источником магнитного поля является ток. Поэтому: Возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им поток магнитной индукции через площадь, ограниченную контуром, стремится компенсировать то изменение потока магнитной индукции, которое вызывает данный ток (правило Ленца). Ток в контуре имеет отрицательное направление ( Поэтому с учетом правила Ленца (знака) выражение для закона электромагнитной индукции записывается: Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой. Если контур (например, катушка) состоит из нескольких витков, то где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную: www.eduspb.com В этом разделе мы рассмотрим только три вида индукции: электромагнитную индукцию, индукцию магнитного поля и электрическую индукцию и основные формулы, при помощи которых данные виды индукции вычисляют. Электрическая индукция (или вектор электрического смещения ( где Для изотропного вещества индукция электрического поля связана с напряженность это поля как: где Самой распространённой формулой, при помощи которой находят величину вектора индукции электростатического поля, является теорема Остроградского – Гаусса: Поток ( Модуль вектора На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора где Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение: где Основными законами, которыми пользуются чаще всего для расчета магнитных полей, являются: закон Био-Савара-Лапласа и теорема о циркуляции вектора магнитной индукции. Если проводник помещен в переменное магнитное поле, то в нем возникает электродвижущая сила – это сущность явления электромагнитной индукции. Основной закон электромагнитной индукции состоит в следующем: ЭДС электромагнитной индукции ( В системе международных единиц (СИ) закон электромагнитной индукции записывают так: где ru.solverbook.comОткрытие Фарадея и Ленца: закон электромагнитной индукции — формула явления. Индукционный ток формула
Электромагнитная индукция – FIZI4KA

Явление электромагнитной индукции

Магнитный поток
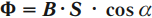
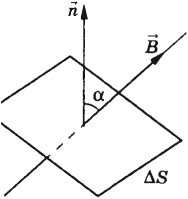

Закон электромагнитной индукции Фарадея
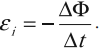
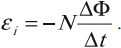
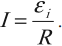

Правило Ленца
Самоиндукция
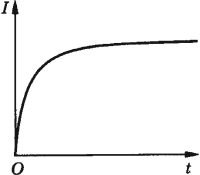

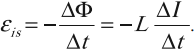
Индуктивность
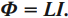
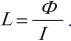
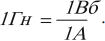
Энергия магнитного поля
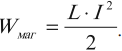
Основные формулы раздела «Электромагнитная индукция»

Репетитор-онлайн — подготовка к ЦТ
формула явления, силы индукционного тока и скорости изменения магнитного потока

Открытие ЭИ
 Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.
Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.Явление ЭИ
Закон
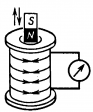
 Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.
Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.Другие законы Фарадея
Вихревые токи
 Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции.
Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции. Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.
Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.Вывод
Электромагнитная индукция
расчет электродвижущей силы по формуле
Законы Фарадея и Ленца
Движение провода в магнитном поле
Вращающаяся катушка
ЭДС самоиндукции
Взаимоиндукция
Видео
Оцените статью: Электромагнитная индукция. | Объединение учителей Санкт-Петербурга
Электромагнитная индукция 
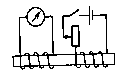

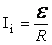 . e не зависит от свойств контура:
. e не зависит от свойств контура: 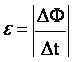 .
. 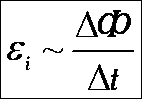
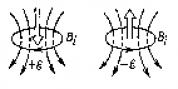
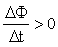 ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю:
; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: 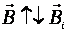 , где
, где  - т.н. индукционное магнитное поле.
- т.н. индукционное магнитное поле.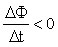 . Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем:
. Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем: 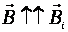 .
. 
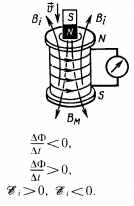
 ),если
),если противоположно
противоположно (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (
(т.е. ΔΦ>0). Ток в контуре имеет положительное направление (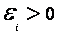 ), если
), если  совпадает с
совпадает с  , (т.е. ΔΦ<0).
, (т.е. ΔΦ<0).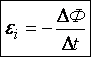 .
. 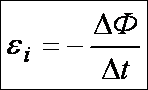
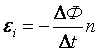 ,
,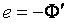 , где e – мгновенное значение ЭДС индукции.
, где e – мгновенное значение ЭДС индукции. 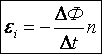
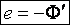
Формула индукции
Формула индукции электрического поля
 )) – это одна из основных векторных характеристик электрического поля. Формулой определяющей вектор электрической индукции является выражение:
)) – это одна из основных векторных характеристик электрического поля. Формулой определяющей вектор электрической индукции является выражение:![Rendered by QuickLaTeX.com \[\overline{D}={\varepsilon }_0\overline{E}+\overline{P} \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f2036b94d2f3b514b51561edd6650e97_l3.png)
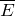 – вектор напряженности электрического поля;
– вектор напряженности электрического поля; 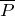 – вектор поляризации;
– вектор поляризации; 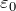 – электрическая постоянная.
– электрическая постоянная. ![Rendered by QuickLaTeX.com \[\overline{D}={\varepsilon }_0\varepsilon \overline{E} \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b8ce707478f2eae43349e1b4d4d252dc_l3.png)
 – диэлектрическая проницаемость вещества.
– диэлектрическая проницаемость вещества. ![Rendered by QuickLaTeX.com \[\Psi_D=\oint_S{\overline{D}d\overline{S}=\oint_S{D_ndS}=Q} \qquad (3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-56b2264e899d0ba19fad5f4d8e01dd89_l3.png)
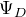 ) вектора электростатической индукции (
) вектора электростатической индукции ( ) в диэлектрике через произвольную замкнутую поверхность равен сумме свободных зарядов, которые находятся внутри рассматриваемой поверхности. В данной форме теорема Гаусса выполняется и для однородной и изотропной среды, так и для неоднородной анизотропной.
) в диэлектрике через произвольную замкнутую поверхность равен сумме свободных зарядов, которые находятся внутри рассматриваемой поверхности. В данной форме теорема Гаусса выполняется и для однородной и изотропной среды, так и для неоднородной анизотропной. Формула вектора индукции магнитного поля
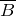 равен частному от деления максимальной силы Ампера (
равен частному от деления максимальной силы Ампера (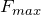 ), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника (
), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ( ):
):![Rendered by QuickLaTeX.com \[B=\frac{F_{max}}{I\Delta l} \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a72cc780cf62d61a0d2a6824d474375b_l3.png)
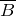 :
:![Rendered by QuickLaTeX.com \[B=\frac{F_L}{qv\sin \alpha \ } } \qquad(5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6298381fd7f607e0cd94f239167b09ce_l3.png)
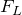 – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле;
– модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; 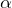 – это угол между векторами
– это угол между векторами 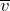 и
и 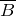 . Направления
. Направления 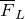 , векторов
, векторов 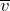 и
и 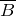 связаны между собой правилом левой руки.
связаны между собой правилом левой руки.![Rendered by QuickLaTeX.com \[B=\frac{M_{max}}{p_m} \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b6519101c2642c4f692f00035b735a3f_l3.png)
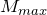 – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом
– максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом 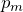 , равным единице, если нормаль к рамке перпендикулярна направлению поля.
, равным единице, если нормаль к рамке перпендикулярна направлению поля.Формула электромагнитной индукции
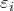 ) в контуре, помещенном в переменное магнитное поле, равна по величине скорости изменения магнитного потока (
) в контуре, помещенном в переменное магнитное поле, равна по величине скорости изменения магнитного потока (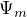 ), который проходит через поверхность, которую ограничивает рассматриваемый контур. При этом знаки ЭДС и скорости изменения магнитного потока противоположны.
), который проходит через поверхность, которую ограничивает рассматриваемый контур. При этом знаки ЭДС и скорости изменения магнитного потока противоположны.![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-08581c9f50951e5c0fa2e6ab1e19e888_l3.png)
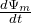 – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур. (Часто индекс у магнитного потока опускают и обозначают его Ф). Когда вычисляют ЭДС индукции и магнитный поток, учитывают то, что направление нормали к плоскости контура (
– скорость изменения магнитного потока сквозь площадь, которую ограничивает контур. (Часто индекс у магнитного потока опускают и обозначают его Ф). Когда вычисляют ЭДС индукции и магнитный поток, учитывают то, что направление нормали к плоскости контура (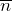 ) и направление его обода связаны. Вектор
) и направление его обода связаны. Вектор 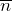 должен быть направлен так, чтобы из его конца обход контура проходил против часовой стрелки.
должен быть направлен так, чтобы из его конца обход контура проходил против часовой стрелки. Примеры решения задач по теме «Индукция»
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''









Поделиться с друзьями: