Формула КПД. Кпд физика формула

Расчет коэффициента полезного действия: формулы для электрической цепи

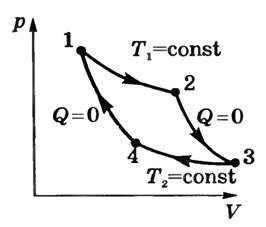
Как известно, на данный момент еще не созданы такие механизмы, которые бы до конца превращали один вид энергии в другой. В процессе работы любой рукотворный прибор расходует часть энергии на сопротивление сил либо же впустую ее рассеивает в окружающую среду. То же самое происходит и в замкнутой электроцепи. Когда заряды протекают по проводникам, осуществляется сопротивление полной и полезной нагрузки работы электричества. Чтобы сопоставить их соотношения, потребуется произвести коэффициент полезного действия (КПД).

Простейшая электрическая цепь

Для чего нужен расчет КПД

Коэффициент полезного действия электрической цепи – это отношение полезного тепла к полному.

Для ясности приведем пример. При нахождении КПД двигателя можно определить, оправдывает ли его основная функция работы затраты потребляемого электричества. То есть его расчет даст ясную картину, насколько хорошо устройство преобразовывает получаемую энергию.

Обратите внимание! Как правило, коэффициент полезного действия не имеет величины, а представляет собой процентное соотношение либо числовой эквивалент от 0 до 1.

КПД находят по общей формуле вычисления, для всех устройств в целом. Но чтобы получить его результат в электрической цепи, вначале потребуется найти силу электричества.

Нахождения тока в полной цепи

По физике известно, что любой генератор тока имеет свое сопротивление, которое еще принято называть внутренняя мощность. Помимо этого значения, источник электричества также имеет свою силу.

Дадим значения каждому элементу цепи:

• сопротивление – r;
• сила тока – Е;
• резистор (внешняя нагрузка) – R.

Полная цепь

Итак, чтобы найти силу тока, обозначение которого будет – I, и напряжение на резисторе – U, потребуется время – t, с прохождением заряда q = lt.

Рассчитать работу источника тока можно по следующей формуле:

A = Eq = EIt.

В связи с тем, что сила электричества постоянна, работа генератора целиком преобразуется в тепло, выделяемое на R и r. Такое количество можно рассчитать по закону Джоуля-Ленца:

Q = I2 + I2 rt = I2 (R + r) t.

Затем приравниваются правые части формулы:

EIt = I2 (R + r) t.

Осуществив сокращение, получается расчет:

E = I(R + r).

Произведя у формулы перестановку, в итоге получается:

I = E R + r.

Данное итоговое значение будет являться электрической силой в данном устройстве.

Произведя таким образом предварительный расчет, теперь можно определить КПД.

Расчет КПД электрической цепи

Мощность, получаемая от источника тока, называется потребляемой, определение ее записывается – P1. Если эта физическая величина переходит от генератора в полную цепь, она считается полезной и записывается – Р2.

Чтобы определить КПД цепи, необходимо вспомнить закон сохранения энергии. В соответствии с ним, мощность приемника Р2 будет всегда меньше потребляемой мощности Р1. Это объясняется тем, что в процессе работы в приемнике всегда происходит неизбежная пустая трата преобразуемой энергии, которая расходуется на нагревание проводов, их оболочки, вихревых токов и т.д.

Чтобы найти оценку свойств превращения энергии, необходим КПД, который будет равен отношению мощностей Р2 и Р1.

Итак, зная все значения показателей, составляющих электроцепи, находим ее полезную и полную работу:

• А полезная. = qU = IUt =I2Rt;
• А полная = qE = IEt = I2(R+r)t.

В соответствии этих значений, найдем мощности источника тока:

• Р2 = А полезная /t = IU = I2 R;
• P1 = А полная /t = IE = I2 (R + r).

Произведя все действия, получаем формулу КПД:

n = А полезная / А полная = Р2 / P1 =U / E = R / (R +r).

У этой формулы получается, что R выше бесконечности, а n выше 1, но при всем этом ток в цепи остается в низком положении, и его полезная мощность мала.

Каждый желает найти КПД повышенного значения. Для этого необходимо найти условия, при которых P2 будет максимален. Оптимальные значения будут:

dP2 / dR = 0.

Далее определить КПД можно формулами:

• P2 = I2 R = (E / R + r)2 R;
• dP2 / dR = (E2 (R + r)2 — 2 (r + R) E2 R) / (R + r)4 = 0;
• E2 ((R + r) -2R) = 0.

В данном выражении Е и (R + r) не равны 0, следовательно, ему равно выражение в скобках, то есть (r = R). Тогда получается, что мощность имеет максимальное значение, а коэффициент полезного действия = 50 %.

Как видно, найти коэффициент полезного действия электрической цепи можно самостоятельно, не прибегая к услугам специалиста. Главное –соблюдать последовательность в расчетах и не выходить за рамки приведенных формул.

Видео

Оцените статью:

elquanta.ru

физика для 7 класса: что такое работа, кпд, время и другие основные понятия предмета

Здравствуйте, дорогие друзья! Сегодня мы рассмотрим основные понятия физики и формулы, которые входят в программу учебника Физика 7 класс. Мы пройдем вкратце весь путь познания в области физики от таких базовых понятий, как объем и масса, до коэффициента полезного действия.

...

Вконтакте

Facebook

Twitter

Google+

Мой мир

Количественные характеристики тела

Основные понятия физики – суть всех понятий, которые прямо или косвенно описывают природу явлений. Из количественных характеристик тела можно отметить его объем и массу. Приведем определение.

Объем представляет собой показатель того, сколько место занимает тело в пространстве. Уточним, что, если, к примеру, полая сфера и шар одинакового радиуса находятся в пространстве, то это не означает, что обе фигуры занимают в пространстве одинаковое количество места. Поясним это подробнее.

Полая сфера только на первый взгляд занимает столько же места, сколько шар, на деле их объемы различны – внутри сферы пустота, поэтому, рассчитывая объем, необходимо понимать, что объем воздуха внутри не входит в общую формулу.

Важно! Объем – величина, которая характеризует исключительно место, занимаемое телом. Объем не отражает суть влияние тела на само пространство и на другие тела. Тела одинаковой формы и размеров из совершенно различных материалов будут иметь одинаковые объемы. Формула объема также будет одинакова, как и его численное значение.

Для того чтобы характеризовать понятие объема, вспомним о том, каким образом мы измеряли размеры фигур на плоскости. Для этого мы пользовались понятием площадь. У плоских фигур не может быть объема, у объемных фигур может быть площадь, она называется площадью поверхности. Роль объема в физике очень велика, так как она отражает суть его размеров.

Приведем формулы некоторых фигур:

Формула объема параллелепипеда:

V = abc,

где abc – стороны.

Пирамиды:

,

где S – основание, Н – высота.

Конуса:

,

где R – радиус основания, Н – высота.

Цилиндра:

?=?,

где R – радиус основания, Н – высота.

Говоря о массе, необходимо помнить, что эта физическая величина, в отличие от объема, как раз отражает влияние тела на окружающие тела. Масса представляет собой меру инерции тела, это физическая величина, которая определяет его гравитационные характеристики.

Не следует путать вес с массой, поскольку вес – это сила, и она зависит от гравитационных условий, в котором тело «взвешивается».

Путь, время, скорость, ускорение

При движении тела оно проходит множество точек. Совокупность этих точек называется траекторией. Вектор между началом движения и концом называется перемещением. Если тело движется равномерно и прямолинейно, то перемещение, путь и расстояния равны.

При движении с постоянной скоростью тело проходит за равные промежутки времени равные отрезки пути. Его путь можно отметить формулой:

S = vt, где:

v – скорость тела, t – время его пути. Понятие скорости в физике является одним из самых базовых, поскольку отражает общую тенденцию движущегося тела.

Если в течение времени t1 тело прошло расстояние S1, затем, изменив свою скорость, прошло расстояние S2 за время t2, то есть смысл говорить о таком понятии, как средняя скорость.

Явление средней скорости в общем понимании можно рассматривать как среднее арифметическое двух его скоростей:

.

Если тело обе части пути проходило одно и то же расстояние S, то формула времени принимает вид:

.

Запишем время как отношение расстояния к скорости:

.

Тогда из этого соотношения можно получить выражение для средней скорости:

.

Если тело движется не с постоянной скоростью, но в течение одинаковых промежутков времени, его скорость одинаково меняется, то есть смысл говорить о равноускоренном движении (либо равнозамедленном, если скорость снижается, т.е. тело тормозит).

Важно! Именно равноускоренно двигаются все падающие тела. Ускорение соответствует ускорению свободного падения.

Введем понятие ускорения. Если тело двигалось со скоростью v0, спустя время t оно начало двигаться со скоростью v, то ускорением называется величина, равная:

В математике подобное отношение также называют производной скорости по времени. Зависимость скорости от каждого момента времени легко получить, отделив из формулы ускорения скорость:

.

Изобразим график зависимости скорости от времени:

Очевидно, что графиком является прямая, причем тангенсом угла наклона этой прямой будет ускорение.

Площадь трапеции под графиком – расстояние, которое прошло тело. Вычислить эту площадь довольно просто, нам известно, что площадь трапеции является полусуммой ее оснований, умноженной на высоту. Одно основание трапеции равно v0 (как раз место, где прямая пересекает координату скорости), второе основание равно v. Высотой трапеции является ее сторона – время, т.е. t. Таким образом, площадь трапеции (пройденное расстояние) будет равна:

.

Поскольку v = v0 + at, получаем:

.

Таким образом, при равноускоренном движении расстояние равно:

.

В случае, если речь идет о свободном падении, то вместо ускорения во все формулы должно быть поставлено ускорение свободного падения g=9,81 м/с2.

v = v0 + gt;

Если начальная скорость равна нулю, то:

.

Графиком зависимости пути от времени будет парабола (поскольку зависимость квадратичная):

Постараемся найти формулу времени для разных типов движений:

При равномерном движении:

.

При равноускоренном движении:

.

Расчет скорости, пути и времени движения

Вес, сила

Если кинематика занимается изучением того, как именно двигаются тела, то динамика подходит к понятию движения более глубоко – она изучают, почему они двигаются именно так. Здесь появляется понятие силы. Что такое сила в динамике? Данная физическая величина численно отражает уровень воздействия одного тела на другое. Измеряется она в ньютонах.

Больше всего физического смысла данной величины отражается в главных четырех законах, которые носят названия «Три закона Ньютона» и «Закон всемирного тяготения».

Первый закон Ньютона гласит, что если сумма всех сил равна нулю, то тело движется равномерно. Не стоит путать «сумма всех сил равна нулю» и «на тело не действуют никакие силы».

Знаменитый второй закон Ньютона устанавливает связь между динамической величиной силы, импульса и ускорения:

,

.

При постоянной массе:

F = ma.

В частности, если ускорение представляет собой ускорение свободного падения g, то сила превращается в вес:

Р = mg

Здесь мы на минуту остановимся и постараемся при помощи этих двух законов Ньютона усвоить несколько важных понятий.

Первый закон Ньютона гласит, что лежащее на поверхности тело хотя и находится в состоянии покоя (относительно земли), тем не менее, на него действуют две силы. Вес:

Р = mg

И нормаль (сила реакции опоры). Сумма этих сил равна нулю. Формула первого закона Ньютона может выглядеть таким образом:

Если .

Вес является величиной относительной с точки зрения планет, на которых находятся тела. Например, часто можно услышать ошибочное высказывание: «масса тела на Луне меньше, чем на Земле». Это не так. Массы на всех планетах одинаковые, а вот вес разный, поскольку различается ускорение свободного падения. Именно поэтому космонавты на Луне с такой легкостью подпрыгивали – их вес на Луне был значительно ниже, чем на Земле, ведь Луна их притягивала к себе не так сильно, как Земля.

Третий закон Ньютона гласит, что сила действия равна силе противодействия. Иными словами, чем сильнее мы давим на тело, тем сильнее оно давит на нас. Этот закон отражает равенство силы тяжести и нормали.

.

,

где Fi — сила инерции.

Если есть система тел, то скорость центра масс системы равна:

.

Три закона Ньютона

Закон всемирного тяготения, который еще называют четвертым законом Ньютона, гласит:

,

где G – гравитационная постоянная, m1, m2  – массы притягивающихся тел.

Если в левой части этого равенства указать вес, то получаем формулу для ускорения свободного падения тел на любой планете:

.

Также, из закона всемирного тяготения выводится понятие первой космической скорости, т.е. скорости, при которой тело покидает гравитационное поле. Именно до этой скорости (на Земле она равна 7,9 км/с) разгоняют ракеты, которые необходимо вывести на орбиту.

Первая космическая скорость:

.

Вернемся к понятию веса.

Если тело находится в состоянии покоя, то вес равен:

Р = mg

Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:

Р = m(g+a)

Если тело движется в системе отсчета, которая движется вверх с ускорением а, то вес равен:

Р = m(g-a)

Эта формула наглядно показывает, что в падающем лифте, где а = g, вес тела будет равен нулю, т.е. тело испытает невесомость.

Если тело движется по выпуклой траектории, то ускорение, действующее на него, – центробежное, а значит вес:

Р=m(g-v2/r).

Если тело движется по вогнутой траектории, то ускорение действующее на него — тоже центробежное и направлена от центра, а значит вес:

Р=m(g+v2/r).

Формула силы трения:

,

где  — коэффициент трения, N — нормаль (реакция опоры).

Таким образом, мы познакомились уже с несколькими видами сил – вес (сила тяжести), сила трения, центробежная сила, сила всемирного тяготения (которая является по сути тем же весом, только в более общей форме).

Рассмотрим еще одну силу, которая имеет место в случае деформаций. Она называется силой упругости. Закон Гука для малых деформаций (сжатий или растяжений) гласит, что сила, действующая на тело, длину которого деформировали на х, равна:

Fупр = –kx.

Из этого закона вытекает ряд следствий, например модуль Юнга, который выступает коэффициентом пропорциональности в связи между нормальным напряжением и относительным изменением длины:

.

Центробежная сила

Энергия, работа, мощность, полезное действие

Для того чтобы описывать различные формы взаимодействия материи и ее движение, вводится физическая величина энергия. Если тело прошло расстояние S из-за того, что на него в это время действовала сила F, то энергия этого движения называет работой этого тела. Формула работы записывается таким образом (произведение силы и пройденного пути):

A = FS

Если тело движется со скоростью v, то тело обладает энергией, которая называется кинетической:

.

Если тело приподняли на высоту h, то оно обладает в точке подъеме потенциальной энергией:

E = mgh/.

Важно ! По сути, потенциальная энергия представляет собой работу силы тяжести. Если сила тяжести mg, а путь, пройденный телом, – высота h, на которую его подняли, то работа A = F

S = mgh.

При падении тела с высоты Н его потенциальная энергия превращается в кинетическую.

Закон сохранения энергии гласит, что в замкнутых системах энергия сохраняется. Таким образом, если тело подняли на высоту h и отпустили, то скорость, с которой оно будет приземляться, можно вычислить из закона сохранения:

.

Отсюда:

.

Остановимся подробнее на двух законах сохранения: законе сохранения энергии и импульса.

Импульс в замкнутых системах сохраняется, энергия в замкнутых системах сохраняется. В паре эти два закона могут разрешить бесконечное количество задач. Рассмотрим пример.

Кинетическая энергия

Задача на закон сохранения энергии и импульса

Задача. Идеально упругий шарик массой m движется со скоростью v и ударяется о покоящийся шарик массой M. Удар будет центральный, т.е. траектория шарика и ось между их центрами – одна и та же линия.

Какая будет скорость u шарика массой M и скорость v1 шарика массой m после удара?

Решение:

Первый шарик до столкновения обладал импульсом mv. Второй шарик находился в состоянии покоя, т.е. его импульс был равен M∙0 = 0.

Таким образом, в системе двух шариков суммарный импульс до столкновения был равен:

.

После столкновения импульс первого шарика стал равен mv1, а импульс второго шарика составил Mu. Тогда суммарный импульс системы двух шариков после удара равен:

Согласно закону сохранения импульса Р = Р1, а именно:

(1).

Теперь рассмотрим энергии. Кинетическая энергия первого шарика до удара составила  . Кинетическая энергия второго шарика равна нулю. После удара первый шарик имеет кинетическую энергию . Второй шарик после удара обладает энергией:.

Согласно закону сохранения энергии:

.

Сократив двойки в знаменателях, получаем:

(2).

Получаем систему из двух выражений (1) и (2).

(*).

Из первого уравнения можем получить выражение для скорости первого шарика после удара:

(3).

Найдем квадрат этой скорости:

.

Найдем значение выражения:

.

Теперь можно подставить это выражение во второе уравнение системы (*):

.

Упрощаем выражение:

.

Выводим квадрат скорости u за скобки:

.

Сокращаем на u:

.

Таким образом, скорость второго шарика после удара составляет:

.

Подставив это в выражение (3), можем найти скорость первого шарика после удара:

.

Это был один из немногих примеров того, каким образом при помощи двух законов сохранения находить величины.

Траты энергии. КПД

Однако, говоря об энергии, следует помнить о ее тратах. Например, если во время работы какой-либо физической системы (движущееся тело или тепловая машина) затраченная энергия Q привела к тому, что система произвела полезную энергию A, то говорят о так называемом коэффициенте полезного действия (КПД). КПД измеряется в процентах, которые численно отображают отношение полезной энергии (которую дает система) ко всей суммарно использованной.

Формулу КПД записывают в таком виде:

,

либо, если в процентах:

.

КПД всегда меньше единицы, поскольку полезная работа не может быть больше суммарной, а закон сохранения энергии должен соблюдаться.

Не существует КПД 100%, поскольку траты (даже самые малые) есть в любых системах.

Скорость движения

 

Сила тяжести — вес тела — 7 класс

uchim.guru

Т. КПД — PhysBook

Коэффициент полезного действия теплового двигателя

Баланс энергии за цикл можно получить на основе первого закона термодинамики. Рабочему телу передано путем теплообмена количество теплоты Q1, и над ним совершена работа A2. Рабочее тело совершило работу при расширении A1 и передало количество теплоты Q2 холодильнику. Для идеального теплового двигателя изменение внутренней энергии ΔU = 0, ибо рабочее тело вернулось в исходное состояние.

\(~Q_1 + A_2 = Q_2 + A_1 .\)

Отсюда

\(~A = A_1 - A_2 = Q_1 - Q_2 .\)

Отношение полезной работы к количеству теплоты, которое рабочее тело получило от нагревателя, называется коэффициентом полезного действия теплового двигателя (КПД):

\(~\eta = \frac{A}{Q_1} = \frac{Q_1 - Q_2}{Q_1} = 1 -\frac{Q_2}{Q_1} . \qquad (1)\)

Из формулы (1) видно, что даже у идеального теплового двигателя η < 1. Наибольший КПД, как показал впервые С. Карно, можно получить для идеального двигателя в случае, если рабочее тело совершает цикл Карно с тем же нагревателем и холодильником. Цикл Карно состоит из двух изотермических (рис. 3 — кривые 1-2 и 3-4) и двух адиабатных (кривые 2-3 и 4-1) процессов:

\(~\eta_{max} = \frac{T_1 - T_2}{T_1} . \qquad (2)\)

Рис. 3

Из формулы (2) видно, что для повышения КПД необходимо увеличивать T1 и уменьшать T2. Так как холодильником в большинстве случаев служит окружающая среда, то основной способ повышения КПД состоит в повышении температуры нагревателя.

Цикл Карно — идеальный цикл. В реальных циклах нельзя осуществить идеальную адиабатность и изотермичность. Кроме того, не устранимы потери на трение. Поэтому КПД в реальных тепловых двигателях всегда меньше, чем рассчитанный по формуле (2).

Из формул (1) и (2) имеем

\(~1 - \frac{Q_2}{Q_1} = 1 - \frac{T_2}{T_1} \Rightarrow \frac{Q_2}{Q_1} = \frac{T_2}{T_1} \Rightarrow \frac{Q_1}{T_1} = \frac{Q_2}{T_2} .\)

где Q2 — количество теплоты, отданной рабочим телом холодильнику, поэтому оно отрицательно.

Следовательно, можно записать алгебраическую сумму:

\(~\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0 .\)

Величина \(~\frac QT\) называется приведенным количеством теплоты.

Следовательно, в цикле Карно сумма приведенных количеств теплоты равна нулю.

Строгий теоретический анализ показывает, что не только для цикла Карно, а для любого обратимого кругового процесса сумма приведенных количеств теплоты равна нулю. Это значит, что в обратимом процессе сохраняется некоторая величина, изменение которой равно приведенному количеству теплоты:

\(~\Delta S = \frac QT .\)

Как показал Р. Клаузиус, S — это энтропия.

Следовательно, в обратимых процессах энтропия не изменяется. При необратимых процессах энтропия замкнутой и адиабатически изолированной системы возрастает: ΔSнеобр > 0.

В общем случае: при любых процессах, протекающих в замкнутой или адиабатически изолированной макроскопической системе, ее энтропия не убывает, т.е. ΔS ≥ 0.

Это заключение можно рассматривать как наиболее общую формулировку второго начала термодинамики.

Из формулы (2) имеем \(~\eta = 1 - \frac{T_2}{T_1}\). Следовательно, видим, что η < 1. КПД был бы η = 1, если бы температура холодильника была равна абсолютному нулю: T2 = 0 К. Но еще в 1912 г. немецкий физик В. Нернст теоретически доказал невозможность достижения такой температуры. Это утверждение называют третьим началом термодинамики; абсолютный нуль темпера туры недостижим; к нему можно лишь асимптотически приближаться.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 163-165.

www.physbook.ru

---

• 
  Приточные системы вентиляции
• 
  Приточные системы вентиляции
• 
  Двигатель для мотоблока нева
• 
  Построить дом дешево
• 
  Как сделать правильно погреб
• 
  Как сделать правильно погреб
• 
  Как правильно шпаклевание или шпатлевание
• 
  Дешево построить дом
• 
  Каталог цветов для сада с фото и названиями
• 
  Каталог цветов для сада с фото и названиями
• 
  Чем утеплить окна на зиму своими руками