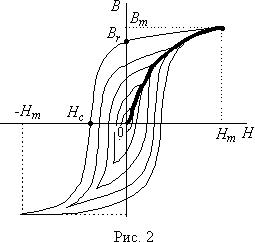
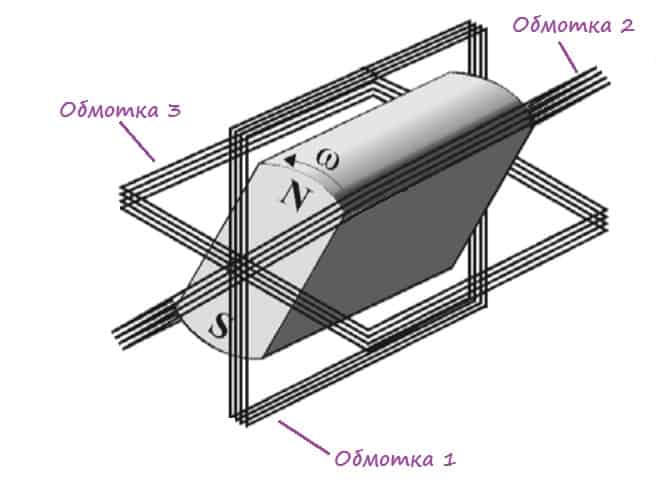
Трёхфазная система электроснабжения — частный случай многофазных систем электрических цепей, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга во времени на определённый фазовый угол. В трёхфазной системе этот угол равен 2π/3 (120°). В трехфазных цепях применяют два вида соединений генераторных обмоток – в звезду и треугольник (рис. 1). При соединении в звезду все концы фазных обмоток соединяют в один узел, называемый нейтральной или нулевой точкой, и обозначают, как правило, буквой O. При соединении в треугольник обмотки генератора соединяют так, чтобы начало одной соединялось с концом другой. ЭДС в катушках в этом случае обозначают соответственно EBA, ECB, EAC. Если генератор не подключен к нагрузке, то по его обмоткам не протекают токи, т.к. сумма ЭДС равна нулю. Рис. 1 Соединения генераторных обмоток – в звезду и треугольник В звезду и треугольник включаются и сопротивления нагрузки так, как показано на рис. 2. Фазные сопротивления Za, Zb, Zc, Zab, Zbc, Zca, соединенные в треугольник или в звезду, называют фазами нагрузки. Напряжение между началом и концом фазы — фазное напряжение Uф, Таким образом, имеется три фазных напряжения—UA, UB и UС. Обычно за условное положительное направление э. д. с. генератора принимают направление от конца к началу фазы. Положительное направление тока в фазах совпадает с положительным направлением э. д. с., а положительное направление падения напряжения (напряжение) на фазе приемника совпадает с положительным направлением тока в фазе. Положительным направлением напряжения на фазе генератора, как и на фазе приемника, является направление от начала фазы к ее концу, т. е. противоположное положительному направлению э. д. с. Напряжение между линейными проводами – линейное напряжение Uл. Таким образом, имеется три линейных напряжения — UAB, UBC, UCA ,условные положительные направления которых приняты от точек, соответствующих первому индексу, к точкам, соответствующим второму индексу. Линейные напряжения определяются через известные фазные напряжения. Это соотношение может быть получено из уравнения, написанного по второму закону Кирхгофа для контура ANBA, если принять направление обхода контура от точки А к точке N и т. д.: UA — UB — UAB = 0. (10.1) Отсюда UAB = UA — UB и, аналогично, UBC = UB – UC , UCA = UC – UA . Таким образом, действующее значение линейных напряжений равно векторной разности соответствующих фазных напряжений.. 23. . Симметричный режим работы трехфазной цепи. Фазовый оператор. Соотношение между фазным и линейным токами и напряжениями в трехфазной цепи при соединении звезда-звезда. Векторная диаграмма. Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями: Трехфазные источники питания практически всегда выполняются симметричными. В этом случае: - действующие значения ЭДС - комплексные, активные, индуктивные сопротивления - фазные коэффициенты мощности - действующие значения фазных напряжений - действующие значения линейных напряжений где Рисунок 8.5 - Векторная диаграмма напряжений при нагрузке «звезда» Из векторной диаграммы видно, что В симметричной трехфазной цепи при соединении фаз звездой действующие фазные и линейные токи равны друг другу, а напряжения отличаются друг от друга в 24. . Симметричный режим работы трехфазной цепи. Фазовый оператор. Соотношение между фазным и линейным напряжениями в трехфазной цепи при соединении треугольник –треугольник. Векторная диаграмма. При соединении трехфазного приемника треугольником при симметричной трехфазной системе: - фазные напряжения оказываются равны линейным напряжениям - действующие значения - фазные коэффициенты мощности - соотношения между линейными и фазными токами по первому закону Кирхгофа для узлов a, b, c где - действующие значения линейных токов - действующие значения фазных токов В симметричной трехфазной цепи при соединении фаз нагрузки треугольником фазные и линейные напряжения равны друг другу, а линейный ток Соотношение между линейными и фазными токами и напряжениями Для соединения обмоток треугольником, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями: Уравнением отвечает векторная диаграмма на рисунке 7. Магнитные цепи. Магнитное поле проводника с током. Магнитное поле катушки с током. Магнитный поток. Магнитная индукция. Намагничивающая сила. Напряженность магнитного поля. Закон Ома для магнитной цепи. Магнитная цепь — последовательность взаимосвязанных магнетиков, по которым проходит магнитный поток. При расчётах магнитных цепей используется почти полная формальная аналогия с электрическими цепями. В простых случаях магнитное поле проводника с током (в том числе и для случая тока, распределённого произвольным образом по объёму или пространству) может быть найдено из закона Био — Савара — Лапласа или теоремы о циркуляции (она же — закон Ампера) Энергию магнитного поля в катушке индуктивности можно найти по формуле: Магни́тный пото́к — поток как интеграл вектора магнитной … Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади. Магнитная индукция, вектор магнитной индукции В, основная характеристика магнитного поля (см. Индукция электрическая и магнитная). Единицей М. и. в Международной системе единиц служит тесла (тл), в СГС системе единиц — гаусс (гс), 1 тл = 10⁴ гс. МАГНИТОДВИЖУЩАЯ СИЛА (мдс) (намагничивающая сила) - характеристика способности источников магнитного поля (электрических токов) создавать магнитные потоки; вводится при расчетах магнитных цепей по аналогии с эдс электрических цепей. Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. 26. Магнитные свойства вещества. Ферромагнитные материалы. Зависимость магнитной индукции от напряженности магнитного поля (петля Гистерезиса). Остаточная магнитная индукция. Коэрцитивная сила. Разделение веществ на диа-, пара- и ферромагнетики носит в значительной степени условный характер, т.к. первые два вида веществ отличаются по магнитным свойствам от вакуума менее чем на 0,05%. На практике все вещества обычно разделяют на ферромагнитные (ферромагнетики) и неферромагнитные, для которых относительная магнитная проницаемость m может быть принятой равной 1,0. К ферромагнетикам относятся железо, кобальт, никель и сплавы на их основе. Они имеют магнитную проницаемость, превышающую проницаемость вакуума в несколько тысяч раз. Поэтому все электротехнические устройства, использующие магнитные поля для преобразования энергии, обязательно имеют конструктивные элементы, изготовленные из ферромагнитного материала и предназначенные для проведения магнитного потока. Такие элементы называются магнитопроводы. Кроме высокой магнитной проницаемости ферромагнетики обладают сильно выраженной нелинейной зависимостью индукции B от напряженности магнитного поля H, а при перемагничивании связь между B и H становится неоднозначной. Функции B(H) имеют особое значение, т.к. только с их помощью можно исследовать электромагнитные процессы в цепях, содержащих элементы, в которых магнитный поток проходит в ферромагнитной среде. Эти функции бывают двух видов: кривые намагничивания и петли гистерезиса. Рассмотрим процесс перемагничивания ферромагнетика. Пусть первоначально он был полностью размагничен. Сначала индукция быстро возрастает за счет того, что магнитные диполи ориентируются по силовым линиям поля, добавляя свой магнитный поток к внешнему. Затем ее рост замедляется по мере того, как количество неориентированных диполей уменьшается и, наконец, когда практически все они ориентируются по внешнему полю рост индукции прекращается и наступает режим насыщения (рис. 1). Если в процессе намагничивания довести напряженность поля до некоторого значения, а затем начать уменьшать, то уменьшение индукции будет происходить медленнее, чем при намагничивании и новая кривая будет отличаться от первоначальной. Кривая изменения индукции при увеличении напряженности поля для предварительно полностью размагниченного вещества называется начальной кривой намагничивания. На рис. 1 она показана утолщенной линией. После нескольких (около 10) циклов изменения напряженности от положительного до отрицательного максимальных значений зависимость B=f(H) начнет повторяться и приобретет характерный вид симметричной замкнутой кривой, называемой петлей гистерезиса. Гистерезисом называют отставание изменения индукции от напряженности магнитного поля. Явление гистерезиса характерно вообще для всех процессов, в которых наблюдается зависимость какой-либо величины от значения другой не только в текущем, но и в предыдущем состоянии, т.е. B2=f(h3, h2) - где h3 и h2 - соответственно текущее и предыдущее значения напряженности. Петли гистерезиса можно получить при различных значениях максимальной напряженности внешнего поля Hm (рис. 2). Геометрическое место точек вершин симметричных циклов гистерезиса называется основной кривой намагничивания. Основная кривая намагничивания практически совпадает с начальной кривой. Симметричная петля гистерезиса, полученная при максимальной напряженности поля Hm (рис. 2), соответствующей насыщению ферромагнетика , называется предельным циклом. Для предельного цикла устанавливают также значения индукции Br при H = 0, которое называется остаточной индукцией, и значение Hc при B = 0, называемое коэрцитивной силой. Коэрцитивная (удерживающая) сила показывает, какую напряженность внешнего поля следует приложить к веществу, чтобы уменьшить остаточную индукцию до нуля. poisk-ru.ru Трехфазная цепь состоит из трех основных элементов: трехфазного генератора, линии передачи со всем необходимым оборудованием, приемников (потребителей). Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями: . Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки. Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки. 15. Ток в нейтральном проводе в трехфазных цепях. Нейтральный (нулевой рабочий) провод — провод, соединяющий между собой нейтрали электроустановок в трёхфазных электрических сетях. При соединении обмоток генератора и приёмника электроэнергии по схеме «звезда» фазное напряжение зависит от подключаемой к каждой фазе нагрузки. В случае подключения, например, трёхфазного двигателя, нагрузка будет симметричной, и напряжение между нейтральными точками генератора и двигателя будет равно нулю. Однако, в случае, если к каждой фазе подключается разная нагрузка, в системе возникнет так называемое напряжение смещения нейтрали, которое вызовет несимметрию напряжений нагрузки. На практике это может привести к тому, что часть потребителей будет иметь пониженное напряжение, а часть повышенное. Пониженное напряжение приводит к некорректной работе подключённых электроустановок, а повышенное может, кроме этого, привести к повреждению электрооборудования или возникновению пожара. Соединение нейтральных точек генератора и приёмника электроэнергии нейтральным проводом позволяет снизить напряжение смещения нейтрали практически до нуля и выровнять фазные напряжения на приёмнике электроэнергии. Небольшое напряжение будет обусловлено только сопротивлением нулевого провода. Трехфазные цепи с нейтральным проводе называют четерехпроводными цепями. Обычно сопротивлением проводов не учитывается / Тогда фазные напр. приемника будут равны фазн. напряжением генератора. . При том что комплексные сопротивления равны , то токи определяются В соответствии с 1 зак. Киргофа ток в нейтр. проводе При симмет. напр. При несим. напр. Нейтр провод выравнивает фазные напряжения. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной. Соединение в звезду На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода. Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки). Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной. Все величины, относящиеся к фазам, носят название фазных переменных, к линии - линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки. Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А, В и С к нейтральной точке N; - фазные напряжения нагрузки. Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать Отметим, что всегда - как сумма напряжений по замкнутому контуру. На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при осно. вании, равными 300), в этом случае (4) Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фаз фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; . Соединение в треугольник В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8). Для симметричной системы ЭДС имеем . Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой. Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9. Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями Аналогично можно выразить линейные токи через фазные токи генератора. На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов . (5) В заключение отметим, что помимо рассмотренных соединений «звезда - звезда» и «треугольник - треугольник» на практике также применяются схемы «звезда - треугольник» и «треугольник - звезда». studfiles.net Чему равен ток в нулевом проводе при симметричной Нулю 55 трехфазной системе токов? Значению, меньшему суммы 34 действующих значений фазных токов Всегда ли векторная сумма токов фаз равняется нулю при Всегда 93 отсутствии нулевого провода? Не всегда 20 Может ли ток в нулевом проводе четырехпроводной цепи Может 66 быть равен нулю? Не может 41 Всегда равен нулю 91 Система ЭДС обмоток трехфазного генератора, работающего в энергосистеме, всегда симметрична: ЭДС поддерживаются строго постоянными по амплитуде и сдвинутыми по фазе на 120°. Рассмотрим симметричную нагрузку (рис. 6.10), для которой ZA=ZB=ZC=Z,ϕA=ϕB=ϕC=ϕ. К зажимам А, В, С подходят провода линии электропередачи— линейные провода. Введем обозначения: Iл— линейный ток в проводах линии электропередачи; Iф—токв сопротивлениях(фазах) нагрузки; Uл—линейноенапряжение между линейными проводами; Uф— фазное напряжение на фазах нагрузки. Врассматриваемой схеме фазные и линейные токи совпадают: Iл=Iф, напряженияUAB, UBC иUCA являются линейными, а напряженияUA, UB, UС — фазными. Складывая напряжения, находим(рис. 6.10): UAB=UA-UB; UBC=UB-UC; UCA=UС-UA. Векторную диаграмму, удовлетворяющую этим уравнениям(рис. 6.11), начинаем строить с изображения звезды фазных напряжений UA, UB, UC. Затем строим векторUAB— как геометрическую сумму векторов UA и—UB, векторUBC — как геометрическую сумму векторовUB и—UC, векторUCA — как геометрическую сумму векторовUC и— UA Рис. 6.10. Соединение нагрузки звездой Рис. 6.11. Полярная векторная диаграмма напряжений Для полноты картины на векторной диаграмме изображены также векторы токов, отстающих на угол ϕ от векторов соответствующих фазных напряжений (нагрузку считаем индуктивной). На построенной векторной диаграмме начала всех векторов совмещены в одной точке (полюсе), поэтому ее называют полярной. Основное достоинство полярной векторной диаграммы — ее наглядность. Рис. 6.12. Топографическая векторная диаграмма Рис. 6.13. Векторная диаграмма фазных и линейных напряжений напряжений при симметричной нагрузке Уравнениям, связывающим векторы линейных и фазных напряжений, удовлетворяет также векторная диаграмма рис. 6.12, которую называют топографической. Она позволяет графически найти напряжение между любыми точками схемы, изображенной на рис. 6.10. Например, для определения напряжения между точкойС и точкой, которая делит пополам сопротивление, включенное в фазуВ, достаточно соединить на векторной диаграмме точкуС с серединой вектораUB. На диаграмме вектор искомого напряжения показан пунктиром. При симметричной нагрузке модули векторов фазных (и линейных) напряжений равны между собой. Тогда топографическую диаграмму можно изобразить так, как показано на рис. 6.13. Опустив перпендикуляр ОМ, из прямоугольного треугольника находим U ф2 Uф U л = U ф2− = 3 . 2 4 2 В симметричной звезде фазные и линейные токи и напряжения связаны соотношениями Iл=Iф;Uл =3UФ. Карточка № 6.3 (189). Соотношения между фазными и линейными напряжениями и токами при симметричной нагрузке в трехфазной цепи, соединенной звездой Какой из токов в схеме линейный, какой— фазный? Оба тока линейные 6 Оба тока фазные 64 Ток I1 — линейный, токI2 — 29 фазный Ток I2 — линейный, токI1 — 105 фазный Между различными точками схемы, изображенной выше, Напряжение UAО — 15 включены вольтметры. Какой из них показывает линейное линейное, напряжение UВО напряжение, какой— фазное? — фазное Напряжение UAB — 78 линейное, напряжениеUBC — фазное Напряжение UCA — 51 линейное, напряжениеUCО — фазное Чему равен вектор UAC, еслиUСА=UC-UА? UAC=-UC-UА. 89 UAC=UА-UC 2 UAC=UC+UА 62 Укажите причину того, что полярная и топографическая Уравнения имеют векторную 36 векторные диаграммы трехфазной цепи удовлетворяют форму одной и той же системе векторных уравнений. Уравнения написаны для 101 симметричной нагрузки Векторы можно переносить 22 параллельно их начальному положению Симметричная нагрузка соединена звездой. Линейное 380 В 74 напряжение 380 В. Определить фазное напряжение. 250 В 44 220 В 85 127 В 9 Ток в нулевом проводе равен нулю при строго симметричной нагрузке. Если нагрузка несимметричная, т. е. ZA¹ZB¹ZС, то неравными будут и токи: IA¹IB¹IС Тогда на основе построения, аналогичного приведенному на рис. 6.8, нетрудно убедиться, что при симметрии фазных напряжений ток в нулевом проводе не равен нулю: I0¹0 (за исключением некоторых частных случаев). Таким образом, при Симметрии фазных напряжений и несимметрии нагрузки в нулевом проводе есть ток. Представим себе, что нулевой провод оборвался: I0=0. При этом токиIA, IB, IС должны измениться так, чтобы их векторная сумма оказалась равной нулю: IA+IB+IС= 0. Но при заданных сопротивлениях нагрузки ZA, ZB, ZС токи могут измениться только за счет изменения фазных напряжений. Следовательно, обрыв нулевого провода в общем случае приводит к изменению фазных напряжений; симметричные фазные напряжения становятся несимметричными. Рассмотрим топографическую векторную диаграмму, представленную на рис. 6.14. Для простоты пренебрежем падением напряжений внутри обмоток генератора и проводах линии и будем считать, что напряжения на нагрузке равны ЭДС генератора. При несимметрии нагрузки и отсутствии нулевого провода фазные напряжения UA, UB, UС будут различными и точкаО' займет на векторной диаграмме положение, отличное от точкиО. Введем нулевой провод с пренебрежимо малым сопротивлением, как показано на рис. 6.7. При этом потенциалы точекО иО' окажутся одинаковыми. Это означает, что точкиО иО' на топографической диаграмме рис. 6.14 должны быть совмещены. Рис. 6.14. Топографическая векторная диаграмма ЭДС и напряжений трехфазной цепи при отсутствии нулевого провода Точка О на топографической диаграмме не может изменить своего положения, так как симметрия ЭДСЕА, ЕВ, ЕС обеспечивается конструкцией генератора. Следовательно, точкаО' перейдет в точкуО, т. е. фазные напряжения на нагрузке станут симметричными. Таким образом, нулевой провод в четырехпроводной цепи предназначен для обеспечения симметрии фазных напряжений при несимметричной нагрузке. Несимметрия фазных напряжений недопустима, так как приводит к нарушению нормальной работы потребителей, рассчитанных на определенное рабочее напряжение. Карточка № 6.4 (233). Назначение нулевого провода в четырехпроводной цепи Может ли геометрическая сумма линейных токов быть отличной Может 60 от нуля при отсутствии нулевого провода? Не может 32 Будут ли меняться линейные токи при обрыве нулевого провода а) Будут; б) не будут 99 в случае: а) симметричной нагрузки; б) несимметричной Будут 18 нагрузки? а) Не будут; б) будут 53 Не будут 71 За счет чего могут измениться линейные токи при постоянной Изменения линейных 82 ЭДС генератора и неизменных сопротивлениях нагрузки? напряжений Изменения фазных 4 напряжений Изменения фазных и 57 линейных напряжений Чему равна разность потенциалов точек О иО' при наличии 0 39 нулевого провода с активным сопротивлением R0? I0R0 96 Uл 26 Может ли нулевой провод, обладающий большим активным Может 69 сопротивлением, обеспечить симметрию фазных напряжений Не может 48 при несимметричной нагрузке? studfiles.net Сегодня мы вернемся к обсуждению основ электроники (ссылка) и обсудим наиболее распространенные в современной энергетике цепи, а именно трехфазные. По сути, приходящее к каждому из нас в квартиру однофазное напряжение (те самые 220 В) есть ни что иное, как одна из фаз от генерируемого на электростанции трехфазного напряжения ) Собственно, в этой статье мы рассмотрим некоторые математические аспекты данного вопроса, а также рассмотрим, какой же смысл кроется в использовании именно таких сигналов. Начнем сразу с преимуществ использования трехфазных цепей. А это, в первую очередь, простота и экономичность генерации. А как, собственно, генерировать переменный трехфазный ток? Для создания цепи необходимы три источника напряжения с одинаковыми частотами и амплитудами, но смещенные друг относительно друга по фазе на 120 градусов. С поставленной задачей отлично справляется синхронный генератор, выполненный по следующей схеме: Генератор состоит из двух частей – ротора и статора – подвижной и неподвижной частей. На статоре расположены три абсолютно одинаковые обмотки, смещенные друг относительно друга на 120 градусов (360 / 3). Ротор же представляет из себя электромагнит, создающий вокруг себя магнитное поле. Суть заключается в том, что при вращении ротора положение магнитного поля и обмоток друг относительно друга меняется, в результате чего в обмотках наводятся синусоидальные сигналы. Для трехфазного напряжения нам нужны синусоидальные напряжения с одинаковой частотой и амплитудой, но отличающиеся по фазе. В данном случае у нас равенство амплитуд гарантируется абсолютной идентичностью конструкции обмоток генератора. Частота сигналов зависит от частоты вращения ротора, а смещение сигналов по фазе обеспечивается тем, что обмотки смещены друг относительно друга в пространстве. Собственно, вот так, в общих чертах, работают генераторы трехфазного напряжения 😉 В итоге мы получаем на обмотках: Если записать действующие значения ЭДС в комплексном виде, то получим следующее: В конце статьи мы обязательно построим векторную диаграмму для этих величин. Чаще всего, кстати, обозначают Давайте перейдем к рассмотрению практического примера подключения потребителя к трехфазной цепи. И тут наиболее “популярным” способом является соединение звездой: Точки A, B и С (начала фаз) соединены с точками a, b и c потребителя. А концы фаз в свою очередь соединены все вместе (точка N) и подключены к точке n приемника. Таким образом, требуется всего 4 провода, которые называются соответственно линейными (A-a, B-b, C-c) и нейтральным (N-n). На заре развития трехфазных цепей концы фаз не соединялись вместе, а просто подключались к концам фаз приемника. В итоге по сути получались три однофазные цепи и для подключения требовалось 6 проводов, а не 4. В связи с экономической невыгодностью такое подключение практически не используется. Давайте теперь на примере соединения звездой рассмотрим некоторые основные термины, использующиеся при работе с такими цепями. В трехфазной цепи различают понятия линейных и фазных напряжений и токов. Фазное напряжение – это напряжение между линейным проводом и нейтральным ( Линейным же напряжением называют напряжение между линейными проводами разных фаз, например И вот как раз-таки еще одним важным преимуществом трехфазных цепей является возможность получения двух величин напряжения в одном генераторе. Давайте определим, собственно, значения этих напряжений. Зная, что сигналы Построим векторную диаграмму: Отсюда геометрически очень просто получить следующее уравнение связи линейных и фазных напряжений: Немного упростим и получим: Поскольку фазные напряжения у нас являются переменными и изменяющимися по синусоидальному закону, то и линейное напряжение будет синусоидальным. Причем связаны фазное и линейное напряжения будут полученным выше соотношением. Рассмотрим “бытовую” трехфазную цепь. К нам в квартиру приходит одна из трех фаз, которая представляет из себя переменное напряжение с действующим значением равным 220В. Каким бы в данном случае было действующее значение линейного напряжения, если бы к нам в квартиру приходили все три фазы? А все просто: 220В * На этом мы на сегодня заканчиваем, надеюсь статья окажется понятной и полезной. До скорых встреч! microtechnics.ru Выдающийся русский инженер-изобретатель Михаил Осипович Доливо-Добровольский, помимо асинхронного двигателя изобрел трехфазную электрическую сеть, которая могла бы питать такой двигатель. Трехфазная система представляет собой три отдельные электрические цепи, в которых действуют синусоидальные ЭДС одной и той же частоты, которые в свою очередь сдвинуты друг от друга на 120°, и создаваемые одним источником энергии. Источником энергии чаще всего выступает трехфазный генератор. Преимущество трехфазной цепи заключается в её уравновешенности. То есть суммарная мгновенная мощность трехфазной цепи, остается величиной постоянной в течение всего периода ЭДС. Трехфазный генератор переменного тока имеет три самостоятельные обмотки, которые сдвинуты между собой на угол 120°. Также как и обмотки, начальные фазы ЭДС сдвинуты на 120°. Уравнения описывающие изменение ЭДС в каждой из обмоток выглядят следующим образом: Векторная диаграмма ЭДС в начальный момент времени представляет собой три вектора, длина которых равна амплитудному значению ЭДС Em, и угол между которыми равен 120°. Если вращать векторы против часовой стрелке, относительно неподвижной оси, то они будут проходить в порядке Ea,Eb,Ec, такой порядок называют прямой последовательностью. По сути, каждую отдельную фазу можно было бы соединить отдельными проводами, но в таком случае получилась бы шестипроводная несвязная система. Это было бы крайне не выгодно с экономичной точки зрения, ведь как-никак, перерасход материала. Для того чтобы это избежать придумали связанные системы соединения. При соединении обмоток звездой все три фазы имеют одну общую точку – ноль. При этом такая система может быть трехпроводной или четырехпроводной. В последнем случае используется нулевой провод. Нулевой провод не нужен, если система симметрична, то есть токи в фазах такой системы одинаковы. Но если нагрузка несимметрична, то фазные токи различны, и в нулевом проводе возникает ток, который равен векторной сумме фазных токов Также, нулевой провод может выступать в роле одной из фаз, если она выйдет из строя, это предотвратит выход из строя всей системы. Правда нужно учитывать, что нулевой провод не рассчитан на подобные нагрузки, и в целях экономии металла и изоляции он изготавливает под более малые токи, чем в фазах. В трехфазных цепях существуют так называемые фазные и линейные напряжения и токи. Фазное напряжение – это разность потенциалов между нулевой точкой и линейным проводом. То есть, проще говоря, фазное напряжение - это напряжение на фазе. Линейное напряжение – это разность потенциалов между линейными проводами. При соединении звездой фазные и линейные напряжения соотносятся как А фазные и линейные токи при симметричной нагрузке одинаковы Таким образом, можно сделать вывод, что в симметричной трехфазной цепи при соединении фаз звездой напряжения отличаются друг от друга в 1,72 раз, а линейные и фазные токи равны. При соединении треугольником конец одной обмотки соединяется с началом другой. Таким образом, образуется замкнутый контур. А фазные и линейные токи соотносятся как Аналогичным способом, сделаем вывод для соединения треугольником: в симметричной трехфазной цепи при соединении фаз треугольником токи отличаются друг от друга в 1,72 раз, а линейные и фазные напряжения равны. Читайте также - задачи на трехфазные цепи electroandi.ru Трехфазная цепь является совокупностью
трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой
частоты, сдвинутые относительно друг друга по фазе на
120o, создаваемые общим источником. Участок
трехфазной системы, по которому протекает одинаковый ток, называется
фазой.
Трехфазная цепь состоит из трехфазного
генератора, соединительных проводов и приемников или нагрузки, которые
могут быть однофазными или трехфазными.
Трехфазный генератор представляет
собой синхронную машину. На статоре генератора размещена обмотка, состоящая
из трех частей или фаз, пространственно смещенных относительно друг
друга на 120o.
В фазах генератора индуктируется симметричная трехфазная система ЭДС,
в которой электродвижущие силы одинаковы по амплитуде и различаются
по фазе на 120o.
Запишем мгновенные значения и комплексы действующих значений ЭДС.
Сумма электродвижущих сил симметричной
трехфазной системы в любой момент времени равна нулю.
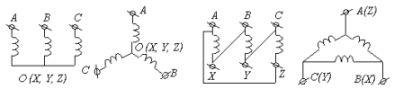
На схемах трехфазных цепей начала
фаз обозначают первыми буквами латинского алфавита (
А, В, С ), а концы - последними буквами (
X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки
генератора к ее началу.
Каждая фаза нагрузки соединяется с фазой генератора
двумя проводами: прямым и обратным. Получается несвязанная трехфазная
система, в которой имеется шесть соединительных проводов. Чтобы уменьшить
количество соединительных проводов, используют трехфазные цепи, соединенные
звездой или треугольником. Если концы всех фаз генератора
соединить в общий узел, а начала фаз соединить с нагрузкой, образующей
трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная
звездой. При этом три обратных провода сливаются в один, называемый
нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена
на рис. 7. 1.
Рис. 7.1 Провода, идущие от источника к
нагрузке называют линейными проводами, провод, соединяющий нейтральные
точки источника Nи приемника N' называют нейтральным (нулевым)
проводом.
Напряжения между началами фаз или между линейными
проводами называют линейными напряжениями. Напряжения между началом
и концом фазы или между линейным и нейтральным проводами называются
фазными напряжениями.
Токи в фазах приемника или источника называют фазными
токами, токи в линейных проводах - линейными токами. Так как линейные
провода соединены последовательно с фазами источника и приемника, линейные
токи при соединении звездой являются одновременно фазными токами.
Iл = Iф.
ZN - сопротивление нейтрального провода.
Линейные напряжения равны геометрическим
разностям соответствующих фазных напряжений
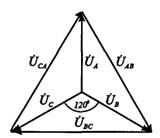
(7.1) На рис. 7.2 изображена векторная
диаграмма фазных и линейных напряжений симметричного источника.
Рис. 7.2 Из векторной диаграммы видно,
что
При симметричной системе
ЭДС источника линейное напряжение больше фазного
в √3 раз.
Uл = √3
Uф Если конец каждой фазы обмотки
генератора соединить с началом следующей фазы, образуется соединение
в треугольник. К точкам соединений обмоток подключают три линейных провода,
ведущие к нагрузке.
На рис. 7.3 изображена
трехфазная цепь, соединенная треугольником. Как видно
из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и
линейные напряжения одинаковы.
Uл = Uф IA, IB,
IC - линейные токи;
Iab, Ibc,
Ica- фазные токи.
Линейные и фазные токи нагрузки
связаны между собой первым законом Кирхгофа для узлов а, b, с.
Рис. 7.3 Линейный ток равен геометрической
разности соответствующих фазных токов.
На рис. 7.4 изображена векторная диаграмма
трехфазной цепи, соединенной треугольником при симметричной нагрузке.
Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы
фазных токов совпадают по направлению с векторами соответствующих фазных
напряжений, так как нагрузка состоит из активных сопротивлений.
Рис. 7.4 Из векторной диаграммы видно,
что
, Iл = √3
Iф при симметричной нагрузке. Трехфазную цепь,
соединенную звездой, удобнее всего рассчитать методом двух узлов.
На рис. 7.5 изображена трехфазная цепь при
соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы
(ZA ≠ ZB ≠ ZC )
Нейтральный провод имеет конечное сопротивление
ZN .
В схеме между нейтральными точками источника
и нагрузки возникает узловое напряжение или напряжение смещения нейтрали.
Это напряжение определяется по формуле (7.2).
Рис.7.5
(7.2) Фазные токи определяются
по формулам (в соответствии с законом Ома для активной ветви):
(7.3) Ток в нейтральном проводе
(7.4) Частные случаи. 1. Симметричная нагрузка. Сопротивления
фаз нагрузки одинаковы и равны некоторому активному сопротивлению
ZA = ZB = ZC = R.
Узловое напряжение
, Напряжения фаз нагрузки
и генератора одинаковы:
Фазные токи одинаковы по
величине и совпадают по фазе со своими фазными напряжениями. Ток
в нейтральном проводе отсутствует
В трехфазной системе, соединенной
звездой, при симметричной нагрузке нейтральный провод не нужен.
На рис. 7.6
изображена векторная диаграмма трехфазной цепи для симметричной нагрузки. 2. Нагрузка несимметричная,
RAB = RC, но сопротивление нейтрального
провода равно нулю: ZN = 0. Напряжение смещения нейтрали
рис. 7.6 Вектор тока в нейтральном
проводе равен геометрической сумме векторов фазных токов.
На рис. 7.7 приведена векторная
диаграмма трехфазной цепи,
соединенной звездой, с нейтральным
проводом, имеющим нулевое
сопротивление, нагрузкой которой
являются неодинаковые по
величине активные сопротивления.
Рис. 7.7 3. Нагрузка несимметричная, RAB = RC, нейтральный провод отсутствует,
Система фазных напряжений
генератора остается симметричной. Это объясняется тем, что источник
трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия
нагрузки не влияет на систему напряжений генератора.
Из-за напряжения смещения нейтрали фазные напряжения
нагрузки становятся неодинаковыми.
Фазные напряжения генератора и нагрузки отличаются
друг от друга. При отсутствии нейтрального провода геометрическая сумма
фазных токов равна нулю.
На рис. 7.8 изображена векторная диаграмма трехфазной
цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы
фазных токов совпадают по направлению с векторами соответствующих фазных
напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме
с несимметричной нагрузкой выравнивает несимметрию фазных напряжений
нагрузки, т.е. с включением данного нейтрального провода фазные напряжения
нагрузки становятся одинаковыми.
Рис. 7.8
Трехфазная цепь является обычной
цепью синусоидального тока с несколькими источниками.
Активная мощность трехфазной цепи равна
сумме активных мощностей фаз
(7.5) Формула (7.5) используется
для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.
При симметричной нагрузке:
При соединении в треугольник
симметричной нагрузки
При соединении в звезду
. В обоих случаях
. nwpi-fsap.narod.ruЦепи трехфазного тока. Соединения звездой и треугольником. Фазные и линейные токи и напряжения. Фазное и линейное напряжение в трехфазных цепях
Цепи трехфазного тока. Соединения звездой и треугольником. Фазные и линейные токи и напряжения.
Поиск Лекций


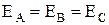 ;
;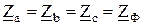 ;
;  ;
; 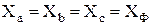 ;
; .
.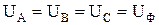 ;
; 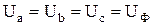
 ,
,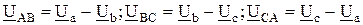 ;
;
 ;
; .
.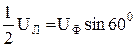 или
или 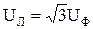 .
. раз
раз ;
; .
.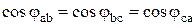 .
.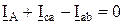 ;
; 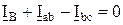 ;
; 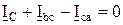 ,
,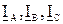 - комплексные линейные токи (IЛ),
- комплексные линейные токи (IЛ), 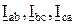 (IФ) - фазные токи.
(IФ) - фазные токи. ;
;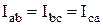 ;
; раз больше фазного
раз больше фазного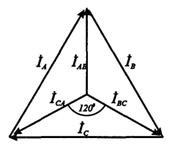


 Эта формула выражает закон Ома для магнитной цепи.
Эта формула выражает закон Ома для магнитной цепи.
13. Элементы трехфазной электрической цепи. Фазные, линейные токи, напряжения.
14. Симметричный и несимметричный приемники в трехфазных цепях, векторные диаграммы.
15 Вопрос Ток в нейтральном проводе в трехфазных цепях.
16 Режимы работы трехфазного премника.
§ 6.3. Cоотношения между фазными и линейными напряжениями и токами при симметричной нагрузке в трехфазной цепи, соединенной звездой
§6.4. Назначение нулевого провода в четырехпроводной цепи
Трехфазные электрические цепи. | MicroTechnics

![Rendered by QuickLaTeX.com \[e_1 = E_msin(wt)\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-7d83c7d2b03b0c009349e045f74d772f_l3.png)
![Rendered by QuickLaTeX.com \[e_2 = E_msin(wt - 2\pi / 3)\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-da9b3f2d920cb5a75efa5d6d9be45da8_l3.png)
![Rendered by QuickLaTeX.com \[e_3 = E_msin(wt - 4\pi / 3) = E_msin(wt + 2\pi / 3)\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-1566a229d8e519d4ccb1c68a87ebe9e5_l3.png)
![Rendered by QuickLaTeX.com \[E_1 = E_me^{j*0}\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-09669b95568f0bf221a8c9c90facb7ae_l3.png)
![Rendered by QuickLaTeX.com \[E_2 = E_me^{j*(-120)}\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-4a5f9d55436aa64577a50dd2e7fa8508_l3.png)
![Rendered by QuickLaTeX.com \[E_3 = E_me^{j*120}\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-b87eb70dfa8c86f156e45dd44e94c906_l3.png)
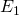 ,
, 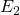 и
и 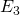 как
как 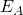 ,
, 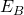 и
и 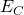 . Пожалуй и мы тоже будем придерживаться такой системы обозначений )
. Пожалуй и мы тоже будем придерживаться такой системы обозначений )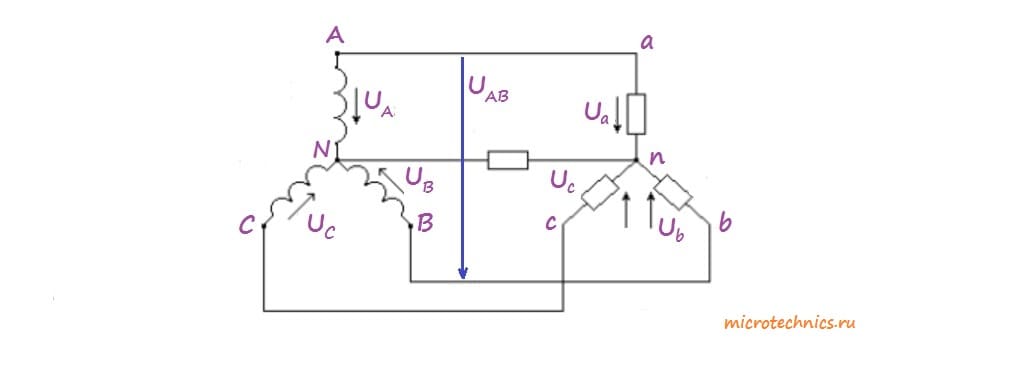
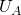 ,
, 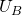 ,
, 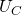 ,
, 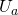 ,
, 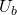 ,
, 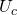 ). Если пренебрегать собственным сопротивлением соединительных проводов, то фазные напряжения приемника равны соответствующим фазным напряжениям источника (
). Если пренебрегать собственным сопротивлением соединительных проводов, то фазные напряжения приемника равны соответствующим фазным напряжениям источника (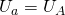 ,
, 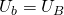 ,
, 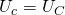 ).
).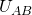 , как на нашей схеме. Аналогично можно определить
, как на нашей схеме. Аналогично можно определить 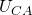 и
и 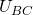 ).
).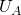 ,
, 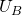 и
и 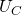 смещены друг относительно друга на 120 градусов, а также учитывая условно выбранные направления напряжений получим следующие уравнения для векторов напряжений (мы рассматриваем именно вектора, а не действующие значения, нельзя путать эти понятия (!)):
смещены друг относительно друга на 120 градусов, а также учитывая условно выбранные направления напряжений получим следующие уравнения для векторов напряжений (мы рассматриваем именно вектора, а не действующие значения, нельзя путать эти понятия (!)):![Rendered by QuickLaTeX.com \[U_{AB} = U_A - U_B\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-fd5677f746ea83f07818d9d2a54b4356_l3.png)
![Rendered by QuickLaTeX.com \[U_{BC} = U_B - U_C\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-0c11e2f78c215891bf47829cda443141_l3.png)
![Rendered by QuickLaTeX.com \[U_{CA} = U_C - U_A\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-c235983787b581148bf31dc278861397_l3.png)
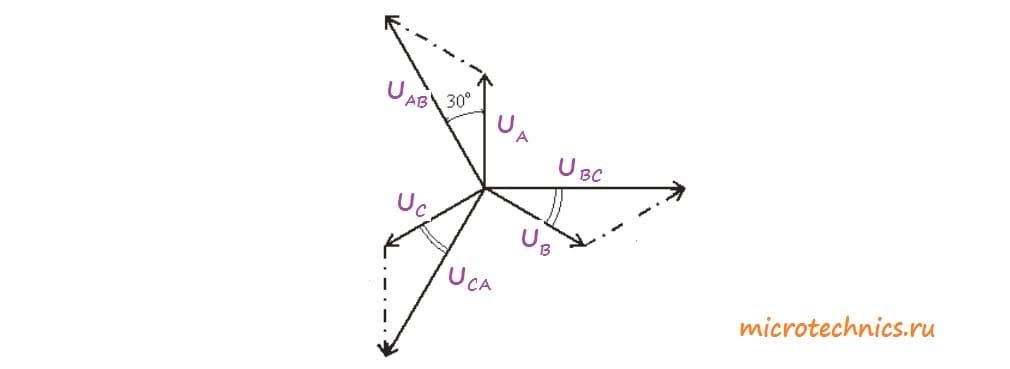
![Rendered by QuickLaTeX.com \[U_{AB} = 2U_Acos(30)\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-407f1b602d5b9827d137125bc7e10ecd_l3.png)
![Rendered by QuickLaTeX.com \[U_{AB} = \sqrt3U_A\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-4a09f776c4044e34b23630f7e73c81ae_l3.png)
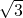 = 380В 😉
= 380В 😉Трехфазные электрические цепи


Соединение звездой





Соединение треугольником
 В таком соединении каждая фаза находится под линейным напряжением, то есть линейные и фазные напряжения равны
В таком соединении каждая фаза находится под линейным напряжением, то есть линейные и фазные напряжения равны 

7.1. Основные определения
7.2. Соединение в звезду.
Схема, определения
7.3. Соединение в треугольник.
Схема, определения
7.4. Расчет трехфазной
цепи, соединенной звездой
7.5. Мощность в трехфазных
цепях
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''









Поделиться с друзьями: