Электри́ческий ток — направленное движение электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Ток – постоянный(I=const действующее значение переменного тока) – переменный (i – мгновенное значение переменного тока) i=ImSin(wt) Напряжение – отношение затраченной энергии для перемещения заряда из одной точки в другую точку цепи. U=dW/dq; W=∫uidt Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. S=P+jQ — полная мощность, ВА (вольт-ампер) — активная мощность, Вт (ватт) — реактивная мощность, ВАр (вольт-ампер реактивный) Название Напряжение ток мощность Активное сопрот. U=Ri i=U/R P=I2R=U2g g=1/R Индуктивное сопрот. uL=Ldi/dt iL=1/L∫uLdt WL=Li2/2 Емкостное сопрот. uC=1/C∫iCdt iC=CduC/dt WC=CU2/2 Баланс мощностей: ∑Pист=∑Pпотр ∑IiEi +∑Jk Uk=∑Ij2 Rj Входные и взаимные проводимости. Входной проводимостью gmm ветви m называется отношение тока Im ветви m к э.д.с. Em источника, помещенного в эту ветвь, при отсутствии э.д.с. в других ветвях:gmm=Im/Em Взамной (передаточной) проводимостью gkm называется отношение тока Ik ветви k к э.д.с. Em источника ветви m. gkm=Ik/Ek Принцип взаимности справедлив для линейных электрических цепей с одним источником э.д.с. и может быть сформулирован следующим образом: если источник э.д.с. E действует в любой ветви сколь угодно сложной цепи, не содержащей других источников э.д.с., вызывает в другой ветви ток I, то будучи перенесенным в последнюю, вызовет в первой ветви такой же ток I. На принципе взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одним источником э.д.с., когда его перенос упрощает расчет цепи. Теорема компенсации. Токи в цепи не изменяются, если любое сопротивление (участок цепи) заменить источником с э.д.с., по величине равной падению напряжения на данном сопротивлении (участке цепи) и направленной навстречу току. Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров. Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком): Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю: Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными. Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным. Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения. Запишем первый закон Кирхгоффа для 4 – 1 узлов: узел 2: I5=I4+I8+J8узел 4: J2+I2=I7+I4узел 1: I7+I6=I1 Запишем второй закон Кирхгофа для трех контуров: контур 15231: I1·R1+I8·R8+I6·(R5+R6)=E8+E6 контур 1341: I1·R1+I2·R2+I7·R7=0 контур 26432: -I4·(R8+R3)-I2·R2+I8·R8=E8 studfiles.net ОСНОВЫ ЭЛЕКТРОНИКИ Напряжение, ток и сопротивление Напряжение и ток — это количественные понятия, о которых следует помнить всегда, когда дело касается электронной схемы. Обычно они изменяются во времени, в противном случае работа схемы не представляет интереса. Напряжение (условное обозначение: U, иногда Е). Напряжение между двумя точками - это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Иначе говоря, это энергия, которая высвобождается, когда единичный заряд «сползает» от высокого потенциала к низкому. Напряжение называют также разностью потенциалов или электродвижущей силой (э. д. с). Единицей измерения напряжения служит вольт. Обычно напряжение измеряют в вольтах (В), киловольтах (1 кВ = 103 В), милливольтах (1 мВ = 10-3 В) или микровольтах (1 мкВ = 10-6 В) (см. раздел «Приставки для образования кратных и дольных единиц измерения», мелким шрифтом). Для того чтобы переместить заряд величиной 1 кулон между точками, имеющими разность потенциалов величиной 1 вольт, необходимо совершить работу в 1 джоуль. (Кулон служит единицей измерения электрического заряда и равен заряду приблизительно 6 - 1018 электронов.) Напряжение, измеряемое в нановольтах (1 нВ = 10-9 В) или в мегавольтах (1 МВ = 106 B) встречается редко; вы убедитесь в этом, прочитав всю книгу. Ток (условное обозначение: I). Ток - это скорость перемещения электрического заряда в точке. Единицей измерения тока служит ампер. Обычно ток измеряют в амперах (А), миллиамперах (1 мА = 10-3 А), микроамперах (1 мкА = 10-6 А), наноамперах (1 нА = 10-9 А) и иногда в пикоамперах (1 пкА = 10-12 А). Ток величиной 1 ампер создаётся перемещением заряда величиной 1 кулон за время, равное 1 с. Условились считать, что ток в цепи протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, хотя электрон перемещается в противоположном направлении. Запомните: напряжение всегда измеряется между двумя точками схемы, ток всегда протекает через точку в схеме или через какой-либо элемент схемы. Говорить «напряжение в резисторе» нельзя - это неграмотно. Однако часто говорят о напряжении в какой-либо точке схемы. При этом всегда подразумевают напряжение между этой точкой и «землёй», то есть такой точкой схемы, потенциал которой всем известен. Скоро вы привыкнете к такому способу измерения напряжения. Напряжение создаётся путём воздействия на электрические заряды в таких устройствах, как батареи (электрохимические реакции), генераторы (взаимодействие магнитных сил), солнечные батареи (фотогальванический эффект энергии фотонов) и т. п. Ток мы получаем, прикладывая напряжение между точками схемы. Здесь, пожалуй, может возникнуть вопрос: а что же такое напряжение и ток на самом деле, как они выглядят? Для того чтобы ответить на этот вопрос, лучше всего воспользоваться таким электронным прибором, как осциллограф. С его помощью можно наблюдать напряжение (а иногда и ток) как функцию, изменяющуюся во времени. Мы будем прибегать к показаниям осциллографов, а также вольтметров для характеристики сигналов. Для начала советуем посмотреть приложение А, в котором идёт речь об осциллографе, и раздел «Универсальные измерительные приборы», мелким шрифтом. В реальных схемах мы соединяем элементы между собой с помощью проводов, металлических проводников, каждый из которых в каждой своей точке обладает одним и тем же напряжением (по отношению, скажем, к земле). В области высоких частот или низких полных сопротивлений это утверждение не совсем справедливо, и в своё время мы обсудим этот вопрос. Сейчас же примем это допущение на веру. Мы упомянули об этом для того, чтобы вы поняли, что реальная схема не обязательно должна выглядеть как её схематическое изображение, так как провода можно соединять по-разному. Рис. 1.1 Закон Кирхгофа для напряжений Запомните несколько простых правил, касающихся тока и напряжения: 1. Сумма токов, втекающих в точку, равна сумме токов, вытекающих из неё (сохранение заряда). Иногда это правило называют законом Кирхгофа для токов. Инженеры любят называть такую точку схемы узлом. Из этого правила вытекает следствие: в последовательной цепи (представляющей собой группу элементов, имеющих по два конца и соединённых этими концами один с другим) ток во всех точках одинаков. 2. При параллельном соединении элементов (рис. 1.1) напряжение на каждом из элементов одинаково. Иначе говоря, сумма падений напряжения между точками А и В, измеренная по любой ветви схемы, соединяющей эти точки, одинакова и равна напряжению между точками А и В. Иногда это правило формулируется так: сумма падений напряжения в любом замкнутом контуре схемы равна нулю. Это закон Кирхгофа для напряжений. 3. Мощность (работа, совершенная за единицу времени), потребляемая схемой, определяется следующим образом: P = U I. Вспомним, как мы определили напряжение и ток, и получим, что мощность равна: (работа/заряд) - (заряд/ед. времени). Если напряжение U измерено в вольтах, а ток I - в амперах, то мощность Р будет выражена в ваттах. Мощность величиной 1 ватт - это работа в 1 джоуль, совершенная за 1 с (1 Вт = 1 Дж/с). Мощность рассеивается в виде тепла (как правило) или иногда затрачивается на механическую работу (моторы), переходит в энергию излучения (лампы, передатчики) или накапливается (батареи, конденсаторы). При разработке сложной системы одним из основных является вопрос определения её тепловой нагрузки (возьмём, например, вычислительную машину, в которой побочным продуктом нескольких страниц результатов решения задачи становятся многие киловатты электрической энергии, рассеиваемой в пространство в виде тепла). В дальнейшем при изучении периодически изменяющихся токов и напряжений мы обобщим простое выражение P = UI. В таком виде оно справедливо для определения мгновенного значения мощности. Кстати, запомните, что не нужно называть ток силой тока - это неграмотно. Нельзя также называть резистор сопротивлением. О резисторах речь пойдёт в следующем разделе. Сигналы www.skilldiagram.com Электрический ток - это направленное движение заряженных частиц.Напряжение- это разность потенциалов между двумя точками цепи.U= dW/dtПотенциал- это количество энергии необходимое для перемещения заряда из точки поля в бесконечность. Источник ЭДС - это источник, который поддерживает на своих зажимах напряжение, изменяющееся по одному и тому же закону независимо от величины и направления тока во внешней цепи. Источник тока - это идеализированный элемент электрической цепи, который поддерживает на своих зажимах ток, изменяющийся по определённому закону независимо от величины и значения напряжения между его зажимами. Источниками электрической энергии являются: гальванические элементы, аккумуляторы, термоэлементы, генераторы в которых происходит преобразование молекулярной, кинетической, тепловой, механической или другого вида энергии в электрическую. Приёмниками электрической энергии являются: электрические лампы, двигатели, электронагревательные приборы в которых происходит преобразование электрической энергии в световую, механическую, тепловую и другие виды энергии. Приёмники электрической энергии часто называют нагрузкой. Теория цепей, как и любая инженерная дисциплина, базируется на понятии моделирования. Физические элементы и явления могут быть описаны приблизительно, идеализированные элементы определяются точно. Взяв некоторую реальную физическую систему, путём различных допущений и упрощений можно построить ряд идеализированных моделей системы, всё более точно соответствующих свойствам реальной цепи. В теории цепей изучают активные и пассивные идеализированные элементы: Ток, напряжение, мощность и энергия в электрических цепях. Ток в проводнике представляет собой явление упорядоченного движения электрических зарядов. Под словом ток понимают также интенсивность или силу тока "жаргон" определяемую количеством электрического заряда прошедшего через поперечное сечение проводника в единицу времени. То есть ток представляет собой скорость изменения заряда во времени. Как отношение двух скалярных величин ток также является скалярной алгебраической величиной, знак которой зависит от направления движения зарядов одного знака, а именно условно принятого положительного заряда. Для однозначного определения направления тока в цепях достаточно выбрать произвольно одно из двух возможных направлений за условно положительное, которое обозначается стрелкой. Если движение положительных зарядов происходит в направлении стрелки , а движение отрицательных зарядов навстречу ей, то ток положительный. При изменении направления движения зарядов ток будет отрицательным. Задать однозначно ток в виде функции времени можно только после указания стрелки тока, или условно положительного направления тока. Причём, на всех участках цепи выбор стрелок производят: i=5A; ( i=-5A)В переменном токе: Если поменять ток:т.е. начальная фаза изменится.Прохождение тока или перенос электрических зарядов в цепях связанны с преобразованием или потреблением энергии. Для нахождения энергии затрачиваемой на перемещение единицы заряда из одной точки проводника в другую вводят величину называемую напряжением. Напряжение - это количество энергии затрачиваемой на перемещение единицы заряда из одной точки проводника в другую.Видно, что напряжение как произведение двух скалярных величин также является скалярной величиной. Для однозначного определения знака напряжения между двумя выводами рассматриваемого участка цепи одному из выводов условно приписывается положительная полярность, которую обозначают либо знаком "+" либо стрелкой направленной от этого вывода: Обычно при расчёте цепей стрелки тока и напряжения выбирают согласованно. В этом случае можно указывать только одну стрелку или тока или напряжения. Если это источник то мощность отрицательна. Мгновенная мощность определённого участка цепи - это скорость изменения энергии затрачиваемой на проведение элементарного заряда по этому участку:Мощность как произведение двух скалярных величин также является скалярной величиной. Знак её определяется знаками напряжения и тока, при совпадении этих знаков мощность положительна, что означает потребление энергии в рассматриваемом участке цепи. При несовпадении этих знаков мощность отрицательна, что означает отдачу её из участка, такой участок называется источником электрической энергии. Идеализированные источники электрической энергии.Под источником напряжения (ЭДС) понимают такой элемент цепи с двумя выводами (полюсами) напряжение между которыми поддерживается в виде некоторой заданной функции времени независимо от тока, отдаваемого во внешнюю цепь.Под источником тока понимают такой элемент цепи, через выводы которого протекает ток с заданным законом изменения во времени, независимо от напряжения появляющегося между выводами. Пассивные элементы цепи.Сопротивление - это такой идеализированный пассивный элемент цепи в котором происходит только необратимое преобразование электромагнитной энергии в тепло или другие виды энергии, а запасание энергии в электрическом и магнитных полях отсутствует. Довольно близки к такому, реальные устройства при относительно небыстрых изменениях токов: U=i * r или i=U * G где G - величина, обратная сопротивлению, называемая проводимостью. В теории линейных электрических цепей ВАХ выглядит: ^ Мощность представляет квадратичную функцию тока или напряжения всегда положительна, т.е. потребляема, или энергия всегда поступает от источника в элемент- это происходит в силу того, что ток и напряжение в элементе в любой момент времени имеют одинаковые знаки.Индуктивным элементом электрической цепи называется такой идеализированный элемент, в котором происходит запасание только магнитной энергии связанное с протеканием тока. Потери и запасание электрической энергии в таком элементе отсутствует. Количественной мерой такого элемента является индуктивность (коэффициент самоиндукции). Индуктивностью чаще всего называют и сам индуктивный элемент. L L-коэффициент самоиндукции.В-индукция (Тесла Тл.) Н-напряженность магнитного поля А/м Ф-поток (Вебер) Φ-потенциалПотокосцепление ψ - это сумма потоков всех витков катушки. Вебер n-количество витков катушки.В индуктивном элементе потокосцепление и ток связанны прямой пропорциональной зависимостью: Коэффициент пропорциональности L - называется коэффициентом самоиндукции или индуктивностью. Индуктивность измеряется в "Генри" (Гн). (*) Индуктивность постоянного тока - это закоротка. В теории линейных цепей коэффициент L считается постоянным и независимым от величины тока катушки. Коэффициент L определяется только геометрическими размерами устройства такое приближение вполне обоснованно при отсутствии ферромагнитных тел. При их наличии индуктивность зависит ещё и от магнитной проницаемости материала сердечника. Линейность кривой намагничивания материала также очень важна, индуктивность постоянна только в том случае, если зависимость ψ от i линейна: Выражение ( * ) позволяет по заданному току определять напряжение если заданно напряжение в элементе, а если требуется определить ток, то нужно проинтегрировать выражение ( * ) Пределы интегрирования обусловлены тем, что ток зависит от знака изменения напряжения и необходимо учитывать всю предысторию элемента. Т.е. при t= мы можем написать, что ток равен нулю. где i(0)- значение тока в элементе в момент времени t=0 . Видно, что это значение не зависит от закона изменения напряжения на элементе до момента t=0. Для определения тока в индуктивности необходимо знать закон изменения напряжения при t >0 и значение тока в момент t=0. Мощность индуктивного элемента: Интегрирование этого уравнения от до t даёт энергию, накопленную элементом к моменту времени t: Энергия в индуктивном элементе не бывает отрицательной её величина пропорциональна значению тока в элементе. Ёмкостным элементом называется идеализированный элемент способный накапливать электрическую энергиюТакой элемент наиболее близок по физическим свойствам к реальному конденсатору с хорошим диэлектриком при относительно невысоких частотах. Известно, что при приложении к такому конденсатору напряжения между обкладками на них появляется электрические заряды противоположных знаков. И между обкладками … (*) где С- измеряется в Фарадах.В теории линейных цепей ёмкость С будем считать постоянной независящей от приложенного напряжения то есть так называемым нулём вольтамперной характеристики. Для получения связи между током и напряжением в емкостном элементе (который часто называют ёмкостью) необходимо продифференцировать по времени соотношение (*)(**) Это выражение позволяет определить ток в ёмкостном элементе по известному закону, изменяя напряжение, приложенное к нему. Если известен ток, а необходимо определить напряжение ёмкостного элемента, то интегрируем соотношение (**) по времени. где - значение напряжения на ёмкости в момент времени t=0Для определения напряжения необходимо знать закон изменения тока в элементе при t>0 и значение напряжения в момент времени t=0. Закон изменения тока в элементе до момента t=0 значения не имеет. Мощность ёмкостного элемента : (***)Мощность может быть как положительной, так и отрицательной.Интегрирование соотношения (***) по времени даёт энергию, накопленную в ёмкостном элементе к моменту времени t. Энергия в ёмкостном элементе всегда положительна и пропорциональна квадрату мгновенного значения напряжения. Основные определения, относящиеся к электрической схеме. Граф цепи. Схема электрической цепи представляет собой схему замещения реального электротехнического устройства. Как она получена, нас не интересует. Этим занимаются специалисты узких специальностей (эл. аппараты, эл. машины). Наша задача определить токораспределение в схеме и искомые напряжения на зажимах ветвей. Для примера рассмотрим следующую схему. Основными понятиями, характеризующими геометрическую конфигурацию цепи, являются: ветвь, узел, контур.Ветвь (в общем случае) – это участок цепи с двумя выводами. Токи или напряжения ветви принимаются в качестве неизвестных, характеризующих состояние цепи. Поэтому, что конкретно понимать под ветвью, зависит от выбранных неизвестных переменных цепи. Ветвью можно считать каждый элемент цепи, но для уменьшения числа переменных за ветви принимаются участки из последовательного соединения нескольких элементов, токи которых равны, и участки из параллельного соединения элементов, напряжения которых равны. Например, (а-е), (с-е).Узел электрической цепи – это точка на схеме, в которой сходятся две или более ветви. Узел из двух ветвей называется устранимым узлом. В большинстве случаев устранимые узлы мы рассматривать не будем.Контуром называется любой замкнутый путь, проходящий через ряд ветвей и узлов.Когда интересуются только геометрической конфигурацией цепей, изображают не элементы, входящие в ветви, а только линии, соединяющие узлы. При этом отвлекаются от физических элементов в ветвях Источники напряжения (ЭДС) заменяют закоротками, а источники тока разрываются. В результате получается скелет схемы, ее геометрический образ, называемый графом цепи. Он состоит из ветвей и узлов. В графе сохраняются число ветвей и узлов, а следовательно и число контуров и узловых пар исходной цепи. Изобразим граф предыдущей схемы: a b c d пример плоского планарного графа e О ветви дерева чень важным понятием является дерево графа. Под ним понимается любая система из минимального числа ветвей графа, соединяющих все узлы без образования замкнутых контуров. По ветвям дерева протекание тока исключено. Для данного графа можно построить 4 дерева. a b e c d a b e c d ветви связи Видно, что количество ветвей дерева на 1 меньше количества узлов цепи: nвд=ny-1 Количество ветвей связи: nвс=nв-nвд=nв-nд+1 Число ветвей, не вошедших в дерево (число ветвей связи): nвс=nв-nну=nв-ny+1Задача анализа цепи. Законы Кирхгофа.Задача анализа цепи формулируется следующим образом: задана схема цепи со значениями параметров всех ее элементов, а также напряжения и токи источников, действующих в цепи. Требуется найти токи и напряжения ветвей, учитывая, что последние связаны ВАХ обычно, обычно определяют или ток или напряжение ветвей. Число искомых неизвестных поэтому считается равным количеству ветвей графа цепи. Для нахождения этих неизвестных требуется составить nв уравнений. Составленные уравнения должны быть линейно независимыми, т.к. любое из них не должно являться линейной комбинацией остальных. Уравнения цепи составляются на основе уравнений Кирхгофа: I-й Закон Кирхгофа является следствием закона сохранения заряда. В узле электрический заряд не накапливается и не расходуется. I-й Закон Кирхгофа: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю. i1+i2-i3-i4-i5=0 II-й Закон Кирхгофа, выражающий закон сохранения энергии, дает уравнение равновесия напряжения в контуре. II-й Закон Кирхгофа: в любой момент времени алгебраическая сумма напряжений ветвей в контуре равна нулю. i1r1+Ue2--i3r3-Ue3=0 Ue2= e2 Ue3= e3 i1r1-i3r3=e3-e2Алгебраическая сумма падения напряжения в пассивных элементах контура равна алгебраической сумме ЭДС в действующем контуре.Знак напряжения определяется выбором стрелок напряжения ветвей. Если при обходе контура стрелка напряжения совпадает с направлением обхода контура, то такому напряжению приписывается «+», если не совпадает – «-».Рассмотрим выбор независимых узлов и контуров, которые дают необходимое и достаточное число линейно независимых уравнений, равновесие токов и напряжений в цепи. Основным признаком независимости одного уравнения от других является наличие в нем какого-то нового неизвестного, которое не входило в другие уравнения: Покажем, что число независимых узлов равно числу ветвей дерева, а число независимых контуров – числу ветвей связи. Рассмотрим дерево графа. a b c d e Видно, что если рассматривать узлы этого дерева в порядке последовательного возрастания числа сходящихся ветвей, то в каждый новый узел, кроме последнего, входит ветвь, не вошедшая в другие предыдущие узлы. Т.е. число независимых узлов на 1 меньше суммарного количества узлов. Последний узел будет давать зависимое уравнение, равное сумме всех уравнений независимых узлов. Т.о., число необходимых и достаточных уравнений, составляемых по I закону Кирхгофа и единственным образом определяющих состояние цепи, равно числу ветвей дерева. Протекание токов по ветвям дерева исключено, т.к. отсутствуют контуры. При присоединении к каждой ветви связи образуется 1 контур, по которому будет протекать ток ветви связи, называемый контурным током. Контуры, число которых будет равно числу ветвей связи, будут независимыми т.к. каждый контур образуется собственной ветвью связи. Т.о., число необходимых и достаточных уравнений, составляемых по II закону Кирхгофа и единственным образом определяющих состояние цепи, равно числу ветвей связи. Метод контурных токов. Введем в рассмотрение контурные токи Iаа, Iбб: i1= Iaa; i2= Iaa+ Iб; i3=- Iаа+ Iбб; i4=- Iбб- Iб; i5= Iбб. Подставим полученные значения действительных токов в соотношения (*). Получим 2 уравнения с двумя неизвестными. После преобразований получим:Iаа(r1+r2+r3)- Iббr3+ Iбr2=e1-e2;Iбб(r4+r3)- Iааr3+ Iбr4=-e5; Метод узловых потенциалов.Метод узловых потенциалов позволяет уменьшить количество составляемых уравнений до их числа полученных по первому закону Кирхгофа. Пусть известны потенциалы всех узлов в рассматриваемой схеме. Тогда токи в ветвях могут быть определены путём составления уравнений по второму закону Кирхгофа: –это стрелка напряжения или разности потенциалов. Подобным образом можно выразить все токи в ветвях. Полученное соотношение для токов подставим в соотношения для узлов 1-3 по, первому закону Кирхгофа получим: Один из потенциалов необходимо принять равным нулю, рекомендуется заземлять один из узлов примыкающих к ветви с нулевым сопротивлением и одним источником ЭДС. Пусть для трёх оставшихся узлов составим уравнения: В первом соотношении в левой и правой частях. Умножим левую и правую части на и устремим к нулю и получим что: Первое соотношение превратится в тождество, уравнение можно было не составлять, а сразу определить потенциал узла 3, обойдя контур 22. Метод наложения.Этот метод является следствием общефизического принципа суперпозиции справедливого только для линейных систем. Этот метод, применяемый к линейным электрическим цепям, заключается в следующем: реакция цепи на воздействие нескольких источников равна сумме реакций на воздействия отдельных источников. Для токов сумма понимается в алгебраическом смысле. Ток, в какой либо ветви многоконтурной цепи с несколькими источниками можно рассматривать как сумму отдельных частичных токов вызванных в соответствующей ветви каждым из источников цепи. zadocs.ruТок, напряжение, мощность и энергия в электрических цепях. Ток напряжение мощность
1.Ток, напряжение, энергия и мощность в электрических цепях. Баланс мощностей.
2.Расчет простейших цепей с одним источником энергии (метод эквивалентных преобразований, входная и взаимная проводимости, принцип взаимности и теорема компенсации)
3.Методы расчета сложных электрических цепей. Метод непосредственного применения законов Кирхгофа (последовательность, особенности и пример расчета)
1.01. Напряжение и ток
Ток, напряжение, мощность и энергия в электрических цепях
Основные понятия линейных электрических цепей:Под электрической цепью понимается совокупность электротехнических устройств, предназначенных для прохождения электрического тока, Электропроцессы в которых могут быть описаны с помощью понятий тока и напряжения.
Основное уравнение элемента, связывающее напряжение и ток в нём (ВАХ - вольтамперная характеристика) закон Ома:
Метод контурных токов позволяет число решаемых уравнений уменьшить до числа уравнений, составляемых по II закону Кирхгофа.Введем в рассмотрение фиктивные контурные токи, алгебраическая сумма которых даст действительный ток в каждой цепи.
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''







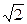





Поделиться с друзьями: