Активная мощность потребляется в активных сопротивлениях, и, в конечном итоге, за счет нее выполняется механическая работа или происходит нагревание резисторов. Реактивная мощность-эта та мощность, которая попросту "болтается в проводах". Она не потребляется активно цепью, но системы передачи оказываются ею загруженными. Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой. Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1): Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и газа и т. п. Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность. Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом: Единица измерения полной мощности S = UI – ВА. Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – В∙Ар. Реактивная мощность Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение. Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %). Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи. Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВ∙Ар на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВ∙Ар/км; воздушная линия 220 кВ – 150 кВ∙Ар/км; подземный кабель 220 кВ – 3 МВ∙Ар/км. Коэффициент мощности и коэффициент реактивной мощности.Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S. Рис. 5.1. Треугольник мощностей Согласно рис. 5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S. Основным нормативным показателем, характеризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P, которое называют коэффициентом реактивной мощности. Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»). Контрольные вопросы лаб. работы № 2 Законы Кирхгофа. Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров. В этом случае законы формулируются следующим образом. Первый закон гласит, что суммарный ток, втекающий в любой узел цепи, равен нулю. Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Второй закон гласит, что суммарное напряжение по любому замкнутому контуру цепи, равно сумме ЭДС, которые в нём находятся. Если в контуре нет ЭДС, то суммарное напряжение равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, то она описывается m − (p − 1) уравнениями напряжений. Законы Кирхгофа –правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа. Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю. Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2. Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения. Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает. Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре. Напряжение выражено как произведение тока на сопротивление (по закону Ома). В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3 совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно: -E1+E2+E3=I1R1-I2R2-I3R3 На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа. Читайте также: lektsia.com Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения. Активная мощность Среднее за период Реактивная мощность Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до —90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Полная мощность Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U×I; связана с активной и реактивной мощностями соотношением: Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: Нелинейные цепи постоянного тока. Понятие статического и дифференциального сопротивления нелинейного элемента. Последовательное соединение линейного и нелинейного элемента. Нелинейные свойства таких цепей определяет наличие в них нелинейных резисторов. В связи с отсутствием у нелинейных резисторов прямой пропорциональности между напряжением и током их нельзя охарактеризовать одним параметром (одним значением Параметры нелинейных резисторов Если нелинейный элемент является безинерционным, то он характеризуется первыми двумя из перечисленных параметров. Под дифференциальным сопротивлением понимается отношение бесконечно малого приращения напряжения к соответствующему приращению тока Следует отметить, что у неуправляемого нелинейного резистора В случае инерционного нелинейного резистора вводится понятие динамического сопротивления определяемого по динамической ВАХ. В зависимости от скорости изменения переменной, например тока, может меняться не только величина, но и знак Переходный процесс – процесс, происходящий в системе после изменения её состояния, и связанный с перераспределением энергии. Коммутация – изменение состояния в электрических цепях. Законы коммутации: ТОК в катушке индуктивности скачком измениться не может. iL(0 − ) = iL(0) = iL(0 + ) НАПРЯЖЕНИЕ на конденсаторе не может измениться скачком. uC(0 − ) = uC(0) = uC(0 + ) Этапы расчета переходного процесса в цепи классическим методом: 1.Найти независимые начальные условия, то есть, напряжения на ёмкостях и токи на индуктивностях в момент начала переходного процесса. 2.Далее необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока i или напряжения u. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе. 3.Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения. 4.Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации. Математическим обоснованием разложения переходного процесса в цепи на принужденный и свободный является известное положение высшей математики: общий интеграл линейного неоднородного дифференциального уравнения равен сумме частного решения неоднородного уравнения и полного решения однородного уравнения. Последнее должно содержать постоянные интегрирования, число которых равно порядку этого дифференциального уравнения. В применении к электрическим цепям определенное частное решение неоднородного уравнения выражает собой принужденный режим, а полное решение однородного уравнения - свободный режим. Переходный процесс в целом выражается общим решением линейного неоднородного дифференциального уравнения, следовательно, суммой принужденной и свободной составляющих. Заряд конденсатора через сопротивление. Разряд конденсатора через сопротивление. Переходные процессы в RL-цепи (подключение к источнику постоянного напряжения, закорачивание катушки с током, скачкообразное увеличение сопротивления). poisk-ru.ru Мощность определяется, как скорость потока энергии, проходящей через
заданную точку. Тоесть мощность – это отношение количества энергии, прошедшей
через данную точку за определённый промежуток времени, к величине этого
промежутка времени. В цепях переменного тока, в отличие от цепей постоянного тока, присутствуют
не только рассеивающие энергию (активные) элементы, но и запасающие энергию
(реактивные) элементы, такие, как индуктивности и ёмкости. Индуктивные элементы
(катушки) запасают энергию в магнитном поле; ёмкостные элементы (конденсаторы)
запасают энергию в электрическом поле. Эти элементы вызывают переодическое
реверсирование потока энергии (энергия переходит из сети в энергию поля
элемента, а затем обратно). Скорость потока энергии, усреднённая за полный период колебания волны
переменного тока, показывающая полезную передачу энергии в одном
направлении, тоесть необратимое рассеяние энергии (преобразование электрической
энергии в другие виды энергии) на активных элементах цепи, известна как
активная мощность (в англ. лит. real power). Максимальное мгновенное (амплитудное) значение скорости циркуляции энергии,
через энергозапасающие (реактивные) элементы цепи, известно как реактивная
мощность (в англ. лит. reactive power). Реактивная мощность
показывает обратимую циркуляцию энергии в системе. Рассеяния энергии на
реактивных элементах нет, так как энергия, полученная реактивными элементами в
течение периода от источника, и, энергия возвращённая реактивными элементами в
течение периода обратно в источник, равны. Инженеры используют несколько терминов для описания потока
энергии в системе: Полная мощность - это модуль векторной суммы активной и
реактивной мощности. На рисунке, P это активная мощность, Q это реактивная мощность (в данном
случае отрицательная), и длина вектора S это полная мощность. Единица измерения всех видов мощностей - это Ватт (символ: Вт / англ. W). Тем не менее, эта единица
измерения зарезервирована для активной компоненты мощности. Полная мощность
традиционно выражается в вольт-амперах (ВА / англ. VA), так как полная мощность есть просто
результат умножения среднеквадратичного напряжения и среднеквадратичного тока.
Единица реактивной мощности обозначается термином «ВАр / англ. VAr», что значит вольт-ампер
реактивный. Так как реактивная мощность не передаёт полезную энергию на
нагрузку, она часто называется «безваттная» мощность («wattless» power). Понимание соотношений между этими тремя величинами лежит в сердце понимания
силовой электротехники. Зависимость между этими величинами может быть выражена
математически с помощью векторов. Так же зависимость между этими величинами
может быть выражена с использованием комплексных чисел: (где j это
мнимая единица). Комплексное число S
называется комплексной мощностью. Рассмотрим идеальную цепь переменного тока состоящую из источника энергии и
обобщённой нагрузки, причём, как ток, так и напряжение, синусоидальные. Если
нагрузка чисто резистивная (то-есть активная), тогда ток и напряжение меняют
полярность одновременно; направление потока энергии не меняет знак и всегда
положительное, поэтому вся мощность (поток энергии) активная. Если нагрузка чисто
реактивная, тогда напряжение и ток различаются по фазе на 90 градусов, и поток
полезной энергии отсутствует. За четверть периода энергия из сети поступает в
реактивную нагрузку (где переходит в энергию магнитного или электрического
поля), а за следующую четверть периода обратно. Максимальное мгновенное
(амплитудное) значение скорости потока энергии, которая циркулирует, в течение
периода, от источника к реактивной нагрузке и обратно, известно как реактивная
мощность. Если ёмкость и индуктивность включены параллельно, тогда токи, текущие через
индуктивность и ёмкость, противоположны и стремятся взаимоуничтожиться быстрее,
чем происходит добавка тока. Обычно считают, что ёмкость генерирует реактивную
мощность, а индуктивность поглащает её. Это есть фундаментальный механизм
контроля коэффициента мощности в системах передачи электрической энергии;
ёмкости (или индуктивности) включаются в цепь с целью частичного уничтожения
реактивной мощности нагрузки. Практически любая нагрузка будет иметь активную,
индуктивную и ёмкостную части, и поэтому, как активная, так и реактивная
мощность, будет поступать в нагрузку. Полная мощность есть произведение среднеквадратичного тока на
среднеквадратичное напряжение. Полная мощность удобна для оценки характеристик
оборудования и проводов/кабелей, так как показывает максимальные значения тока
и напряжения в системе. Тем не менее, если две разные нагрузки характеризуются
определёнными значениями полной
мощности, то их сумма не даст точного значения полной мощности суммарной нагрузки,
если обе нагрузки не имеют одинакового смещения (сдвига фаз) между током и
напряжением. Отношение активной мощности к полной мощности в цепи называется
коэффициентом мощности. Для всех случаев, когда формы тока и напряжения чисто
синусоидальные, коэффициент мощности равен косинусу угла сдвига фаз (φ) между синусоидами тока и
напряжения. По этой причине, в технических характеристиках оборудования часто
обозначают коэффициент мощности как "cosφ". Коэффициент мощности равен 1, когда фазы напряжения и тока совпадают, и
равен нулю, когда ток опережает или отстаёт от напряжения на 90 градусов.
Коэффициент мощности определяется как опережающий или отстающий. Для двух
систем, передающих одинаковое количество активной мощности, система с более
низким коэффициентом мощности будет иметь более высокие значения циркулирующих
в системе токов, благодаря энергии, возвращаемой в источник из энергозапасающих
элементов нагрузки. Эти более высокие токи в реальной системе приведут к более
высоким потерям и уменьшат общую эффективность передачи энергии. Цепь с более
низким коэффициентом мощности будет иметь более высокую полную мощность и более
высокие потери для тогоже количества передаваемой активной мощности. Ёмкостные цепи вызывают реактивную мощность, причём синусоида тока опережает
синусоиду напряжения на 90 градусов. Индуктивные цепи вызывают реактивную
мощность, причём синусоида тока отстаёт от
синусоиды напряжения на 90 градусов. Результатом этого является
стремление индуктивных и ёмкостных элементов уничтожить вырабатываемую
реактивную мощность друг друга соответственно. В системах передачи и распределения энергии, значительные усилия прилагаются
для контроля реактивной мощности. Обычно это делается автоматически путём
подключения и отключения больших массивов дросселей (реакторов) или
конденсаторов, настройкой системы возбуждения генератора и другими методами.
Компании дистрибьюторы электроэнергии могут использовать счётчики
электроэнергии, которые измеряют реактивную мощность с целью выявления и
штрафования пользователей с нагрузками, имеющими низкий коэффициент мощности.
Особенно описанные меры относятся к пользователям эксплуатирующим высоко
индуктивные нагрузки, такие, как моторы на насосных станциях. В то время, как активная мощность и реактивная мощность точно определены в
любой системе, определение полной мощности для несбалансированных многофазных
систем считается одной из самых спорных тем в силовой электротехнике.
Первоначально термин «полная мощность» возник просто как оценка качества
системы. Формирование и план концепции приписываются Виллиаму Стэнли (Феномен
запаздывания в катушке индуктивности, 1888) и Чарльзу Штейнмитцу (Теоретические
элементы проектирования, 1915). Тем не менее, с развитием трёхфазных систем
переменного тока, стало ясно, что определение полной мощности и коэффициента
мощности не может быть применено к несбалансированным многофазным системам. В
1920 году Специальный Объединённый комитет
Американского Института Инженеров-Электриков (AIEE) и Национальная Ассоциация
Электрического Освещения встретились, чтобы решить эту проблему. Они
рассмотрели два определения: В этом случае коэффициент мощности определён, как отношение суммы активных
мощностей всех фаз к сумме полных мощностей всех фаз. Обычно этот метод
применяется в приборах измеряющих параметры сети. В этом случае коэффициент мощности определён, как отношение суммы активных
мощностей всех фаз к модулю суммы комплексных мощностей всех фаз. В 1920 году комитет не нашёл согласия по этому вопросу. В дальнейшем
доминировали дискуссии по этой теме. В 1930 году был сформирован другой комитет
и повторно оказался не в состоянии решить вопрос. Расшифровки стенограмм
дискуссий самые длинные и самые спорные из когда либо опубликованных AIEE (Эмануэль, 1993).
Окончательное решение по этому вопросу не было достигнуто до конца 1990-ых. Идеальный резистор не накапливает энергию, фаза тока и напряжения совпадают.
Поэтому реактивной составляющей мощности нет и P = S. Поэтому для идеального
резистора: Для идеальной ёмкости или индуктивности, с другой стороны, нет передачи
полезной мощности, так как вся мощность реактивная. Поэтому для идеальной ёмкости
или индуктивности: Где X это реактивное сопротивление (англ.
reactance) ёмкости или
индуктивности. Если определить величину X
как положительную для индуктивности и отрицательную для ёмкости, тогда мы можем
убрать знаки модуля (для Q и X)
из уравнения выше. (В этом разделе знак тильда (~) будет использован для обозначения векторов
или комплексных величин, а буквы без дополнительных знаков обозначают модули
векторов соответствующих величин.) Рассмотрим, скажем, последовательную цепь состоящую из активного
(резистивного) сопротивления и реактивного сопротивления. Используя все, что
было сказано выше, мы можем записать следующее выражение: это выражение можно упростить: примем следующее обозначение комплексного сопротивления (комплексного
импеданса): тогда Умножение комплексного числа на сопряжённое с ним комплексное число даёт
квадрат модуля этого числа (тоесть действительное число которому на комплексной
плоскости соответствует вектор, угол которого равен 0): Закон Ома для переменного тока: Из свойств сопряжённых комплексных чисел отсюда следует: Подставляя последние три выражения в выражение для мощности получим: Приведённое выше определение полной мощности применимо и к многочастотным
системам, так как среднеквадратичное значение (СКЗ / англ. RMS) тока и напряжения может быть вычислено для любой
формы волны и следовательно отсюда может быть вычислена полная мощность. Для вычисления активной мощности, казалось бы, мы должны вычислить
произведение тока и напряжения (причем и ток и напряжение есть сумма нескольких
синусоид с разными частотами) и усреднить его. Тем не менее, если внимательно
посмотреть на одно из слагаемых, полученных в результате перемножения тока на
напряжение, мы придём к интересному результату. Конечно усреднение по времени функции вида cos(ωt + k)
есть ноль при условии, что ω не равно нулю. Поэтому единственные слагаемые, которые не будут
равны нулю после усреднения – это те, для которых частота напряжения равна
частоте тока (в примере выше это второе слагаемое, которое при ω1 = ω2 не зависит от времени и
поэтому при усреднении не равно нулю). Другими словами, активную (усреднённую)
мощность можно вычислить просто вычислив активные мощности для каждой частоты
по отдельности, а затем все полученные мощности сложить. Реактивная мощность, в случае многочастотной системы, так
же находится как сумма реактивных мощностей всех гармоник. Тем не менее при
измерении реактивной мощности в многочастотных цепях переменного тока используют
упрощённый метод расчёта реактивной мощности – метод замены несинусоидальных
токов и напряжений эквивалентными синусоидальными. Обычно этот метод
применяется в приборах измеряющих параметры сети. В этом случае: Коэффициент мощности при этом определяется как: Если мы примем за условие, что напряжение в сети имеет единственную частоту
(как это обычно и бывает), то это покажет, что гармонические токи очень плохая
вещь. Они будут увеличивать среднеквадратичное значение тока (за счёт
дополнительных добавок не равных нулю) и так же следовательно увеличивать
полную мощность, но они не окажут влияния на передачу активной мощности.
Следовательно, гармонические токи будут уменьшать коэффициент мощности. Гармонические токи могут быть уменьшены с помощью фильтра, установленного на
входе устройства. Обычно такой фильтр состоит только из ёмкостной цепи (в этом
случае роль индуктивных и резистивных элементов фильтра играют паразитные
сопротивление и индуктивность сетевого источника питания) или из
индуктивно-ёмкостной электрической цепи. Цепь активной коррекции коэффициента
мощности (active power factor correction APFC),
установленная на входе устройства, ещё более эффективно уменьшает гармонические
токи и, следовательно, ещё более приближает коэффициент мощности к
единице. electron287.narod.ruВ чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения? Реактивная мощность единица измерения
В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения?
⇐ ПредыдущаяСтр 4 из 4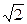 Usin(ωt) и потребляет синусоидальный ток i(t) =
Usin(ωt) и потребляет синусоидальный ток i(t) = 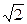 I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением
I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением p(t) = u(t) ∙i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ - UI cos (2ωt -φ)
(5.1)

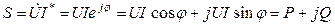 .
.
(5.2)
 не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.
не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.




Мощность в цепях синусоидального тока. Активная, реактивная, полная и комплексная. Единицы измерения.
Поиск Лекций
 значение мгновенной мощности называется активной мощностью:
значение мгновенной мощности называется активной мощностью:  . В цепях однофазного синусоидального тока
. В цепях однофазного синусоидального тока 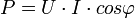 , где
, где  и
и  — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле
— действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле  . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи. С полной мощностью S активная связана соотношением
. В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи. С полной мощностью S активная связана соотношением  . Единица активной мощности — ватт (W, Вт).
. Единица активной мощности — ватт (W, Вт). (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Единица реактивной мощности — вольт-ампер реактивный (var, вар).Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением:
(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Единица реактивной мощности — вольт-ампер реактивный (var, вар).Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: 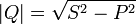 .
. , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (V*A, В*А).
, где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (V*A, В*А).
 ). Соотношение между этими величинами в общем случае зависит не только от их мгновенных значений, но и от производных и интегралов по времени.
). Соотношение между этими величинами в общем случае зависит не только от их мгновенных значений, но и от производных и интегралов по времени. В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления.
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления. Статическое сопротивление равно отношению напряжения на резистивном элементе к протекающему через него току. В частности для точки 1 ВАХ на рис. 1
Статическое сопротивление равно отношению напряжения на резистивном элементе к протекающему через него току. В частности для точки 1 ВАХ на рис. 1 .
.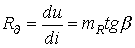 .
. всегда, а
всегда, а  может принимать и отрицательные значения (участок 2-3 ВАХ на рис. 1).
может принимать и отрицательные значения (участок 2-3 ВАХ на рис. 1). ,
,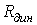 .
. 16. Законы коммутации. Классический метод анализа переходных процессов. Свободный и принужденный процессы.
16. Законы коммутации. Классический метод анализа переходных процессов. Свободный и принужденный процессы.AC power
http://en.wikipedia.org
Wikipedia, свободная энциклопедия
Активная (real),
реактивная (reactive) и полная (apparent) мощность.
Коэффициент мощности (Power factor)
Реактивная
мощность
Несбалансированные
многофазные системы
Основные вычисления с использованием реальных чисел.
Общие вычисления с использованием векторов и комплексных
чисел.
Многочастотные
системы.
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: