РАБОТА И МОЩНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА. ПОНЯТИЕ КОЭФФИЦИЕНТА МОЩНОСТИ. Работа и мощность переменного тока
Работа и мощность переменного тока определение
Электрическая мощность
| Классическая электродинамика |
|
| Электричество · Магнетизм |
Электростатика
|
| Закон Кулона
Теорема Гаусса
Электрический дипольный момент
Электрический заряд
Электрическая индукция
Электрическое поле
Электростатический потенциал |
Магнитостатика
|
| Закон Био — Савара — Лапласа
Закон Ампера
Магнитный момент
Магнитное поле
Магнитный поток
Магнитная индукция |
Электродинамика
|
| Векторный потенциал
Диполь
Потенциалы Лиенара — Вихерта
Сила Лоренца
Ток смещения
Униполярная индукция
Уравнения Максвелла
Электрический ток
Электродвижущая сила
Электромагнитная индукция
Электромагнитное излучение
Электромагнитное поле |
Электрическая цепь
|
| Закон Ома
Законы Кирхгофа
Индуктивность
Радиоволновод
Резонатор
Электрическая ёмкость
Электрическая проводимость
Электрическое сопротивление
Электрический импеданс |
Ковариантная формулировка
|
| Тензор электромагнитного поля
Тензор энергии-импульса
4-потенциал
4-ток |
Известные учёные
|
| Генри Кавендиш
Майкл Фарадей
Никола Тесла
Андре-Мари Ампер
Густав Роберт Кирхгоф
Джеймс Клерк (Кларк) Максвелл
Генри Рудольф Герц
Альберт Абрахам Майкельсон
Роберт Эндрюс Милликен |
|
| См. также: Портал:Физика |
Электрическое напряжение Сила токаЭлектрическая мощность Электрическое сопротивление Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A {\displaystyle A} в точку B {\displaystyle B} , к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки A {\displaystyle A} в точку B {\displaystyle B} . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:
U {\displaystyle U} — напряжение на участке A − B {\displaystyle A-B} (принимаем его постоянным на интервале Δ t {\displaystyle \Delta t} ), Q {\displaystyle Q} — количество зарядов, прошедших от A {\displaystyle A} к B {\displaystyle B} за время Δ t {\displaystyle \Delta t} , A {\displaystyle A} — работа, совершённая зарядом Q {\displaystyle Q} при движении по участку A − B {\displaystyle A-B} , P {\displaystyle P} — мощность. Записывая вышеприведённые рассуждения, получаем:
P A − B = A Δ t {\displaystyle P_{A-B}={\frac {A}{\Delta t}}} Для единичного заряда на участке A − B {\displaystyle A-B} :
P e ( A − B ) = U Δ t {\displaystyle P_{e(A-B)}={\frac {U}{\Delta t}}} Для всех зарядов:
P A − B = U Δ t ⋅ Q = U ⋅ Q Δ t {\displaystyle P_{A-B}={\frac {U}{\Delta t}}\cdot {Q}={U}\cdot {\frac {Q}{\Delta t}}} Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть I = Q Δ t {\displaystyle I={\frac {Q}{\Delta t}}} по определению, в результате получаем:
P A − B = U ⋅ I {\displaystyle P_{A-B}=U\cdot I} . Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p ( t ) {\displaystyle p(t)} , выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u ( t ) {\displaystyle u(t)} и силы тока i ( t ) {\displaystyle i(t)} на этом участке:
p ( t ) = u ( t ) ⋅ i ( t ) . {\displaystyle p(t)=u(t)\cdot i(t).} Если участок цепи содержит резистор c электрическим сопротивлением R {\displaystyle R} , то
p ( t ) = i ( t ) 2 ⋅ R = u ( t ) 2 R {\displaystyle p(t)=i(t)^{2}\cdot R={\frac {u(t)^{2}}{R}}} . Дифференциальные выражения для электрической мощности
Мощность, выделяемая в единице объёма, равна:
w = d P d V = E ⋅ j {\displaystyle w={\frac {dP}{dV}}=\mathbf {E} \cdot \mathbf {j} } , где E {\displaystyle \mathbf {E} } — напряжённость электрического поля, j {\displaystyle \mathbf {j} } — плотность тока. Отрицательное значение скалярного произведения (векторы E {\displaystyle \mathbf {E} } и j {\displaystyle \mathbf {j} } противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.
В случае изотропной среды в линейном приближении:
w = σ E 2 = E 2 ρ = ρ j 2 = j 2 σ {\displaystyle w=\sigma E^{2}={\frac {E^{2}}{\rho }}=\rho j^{2}={\frac {j^{2}}{\sigma }}} , где σ = d e f 1 ρ {\displaystyle \sigma \,{\overset {\underset {\mathrm {def} }{}}{=}}\,{\frac {1}{\rho }}} — удельная проводимость, величина, обратная удельному сопротивлению.
В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:
w = σ α β E α E β {\displaystyle w=\sigma _{\alpha \beta }E_{\alpha }E_{\beta }} , где σ α β {\displaystyle \sigma _{\alpha \beta }} — тензор проводимости.
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
P = I ⋅ U {\displaystyle P=I\cdot U} . Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
P = I 2 ⋅ R = U 2 R {\displaystyle P=I^{2}\cdot R={\frac {U^{2}}{R}}} , где R {\displaystyle R} — электрическое сопротивление. Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
P = I ⋅ E {\displaystyle P=I\cdot {\mathcal {E}}} , где E {\displaystyle {\mathcal {E}}} — ЭДС. Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность p = I 2 ⋅ r {\displaystyle p=I^{2}\cdot r} прибавляется к поглощаемой или вычитается из отдаваемой.
Мощность переменного тока
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ {\displaystyle \varphi } (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность
Единица измерения — ватт (русское обозначение: Вт; международное: W).
P = U ⋅ I ⋅ cos φ {\displaystyle P=U\cdot I\cdot \cos \varphi } .
Среднее за период T {\displaystyle T} значение мгновенной мощности называется активной электрической мощностью или электрической мощностью: P = 1 T ∫ 0 T p ( t ) d t {\displaystyle P={\frac {1}{T}}\int \limits _{0}^{T}p(t)dt} . В цепях однофазного синусоидального тока P = U ⋅ I ⋅ cos φ {\displaystyle P=U\cdot I\cdot \cos \varphi } , где U {\displaystyle U} и I {\displaystyle I} — среднеквадратичные значения напряжения и тока, φ {\displaystyle \varphi } — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r {\displaystyle r} или её проводимость g {\displaystyle g} по формуле P = I 2 ⋅ r = U 2 ⋅ g {\displaystyle P=I^{2}\cdot r=U^{2}\cdot g} . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S {\displaystyle S} активная связана соотношением P = S ⋅ cos φ {\displaystyle P=S\cdot \cos \varphi } .
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Реактивная мощность
Единица измерения — вольт-ампер реактивный (русское обозначение: вар; международное: var)[1].
Q = U ⋅ I ⋅ sin φ {\displaystyle Q=U\cdot I\cdot \sin \varphi } .
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U {\displaystyle U} и тока I {\displaystyle I} , умноженному на синус угла сдвига фаз φ {\displaystyle \varphi } между ними: Q = U ⋅ I ⋅ sin φ {\displaystyle Q=U\cdot I\cdot \sin \varphi } (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S {\displaystyle S} и активной мощностью P {\displaystyle P} соотношением: | Q | = S 2 − P 2 {\displaystyle |Q|={\sqrt {S^{2}-P^{2}}}} .
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина sin φ {\displaystyle \sin \varphi } для значений φ {\displaystyle \varphi } от 0 до плюс 90° является положительной величиной. Величина sin φ {\displaystyle \sin \varphi } для значений φ {\displaystyle \varphi } от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = U I sin φ {\displaystyle Q=UI\sin \varphi } , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
Полная мощность
Единица полной электрической мощности — вольт-ампер (русское обозначение: В·А; международное: V·A)[1].
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I {\displaystyle I} в цепи и напряжения U {\displaystyle U} на её зажимах: S = U ⋅ I {\displaystyle S=U\cdot I} ; связана с активной и реактивной мощностями соотношением: S = P 2 + Q 2 , {\displaystyle S={\sqrt {P^{2}+Q^{2}}},} где P {\displaystyle P} — активная мощность, Q {\displaystyle Q} — реактивная мощность (при индуктивной нагрузке Q > 0 {\displaystyle Q>0} , а при ёмкостной Q 0 {\displaystyle Q
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Комплексная мощность
Мощность, аналогично импедансу, можно записать в комплексном виде:
S ˙ = U ˙ I ˙ ∗ = I 2 Z = U 2 Z ∗ , {\displaystyle {\dot {S}}={\dot {U}}{\dot {I}}^{*}=I^{2}\mathbb {Z} ={\frac {U^{2}}{\mathbb {Z} ^{*}}},} где U ˙ {\displaystyle {\dot {U}}} — комплексное напряжение, I ˙ {\displaystyle {\dot {I}}} — комплексный ток, Z {\displaystyle \mathbb {Z} } — импеданс, * — оператор комплексного сопряжения. Модуль комплексной мощности | S ˙ | {\displaystyle \left|{\dot {S}}\right|} равен полной мощности S {\displaystyle S} . Действительная часть R e ( S ˙ ) {\displaystyle \mathrm {Re} ({\dot {S}})} равна активной мощности P {\displaystyle P} , а мнимая I m ( S ˙ ) {\displaystyle \mathrm {Im} ({\dot {S}})} — реактивной мощности Q {\displaystyle Q} с корректным знаком в зависимости от характера нагрузки.
Измерения
- Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
- Для измерения коэффициента реактивной мощности применяют фазометры
- Государственный эталон — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ
Мощность некоторых электрических приборов
В таблице указаны значения мощности некоторых потребителей электрического тока:
Электрический прибор Мощность,Вт |
| лампочка фонарика |
1 |
| сетевой роутер, хаб |
10…20 |
| системный блок ПК |
100…1700 |
| системный блок сервера |
200…1500 |
| монитор для ПК ЭЛТ |
15…200 |
| монитор для ПК ЖК |
2…40 |
| лампа люминесцентная бытовая |
5…30 |
| лампа накаливания бытовая |
25…150 |
| Холодильник бытовой |
15…700 |
| Электропылесос |
100… 3000 |
| Электрический утюг |
300…2 000 |
| Стиральная машина |
350…2 000 |
| Электрическая плитка |
1 000…2 000 |
| Сварочный аппарат бытовой |
1 000…5 500 |
| Двигатель лифта невысокого дома |
3 000...15 000 |
| Двигатель трамвая |
45 000…50 000 |
| Двигатель электровоза |
650 000 |
| Электродвигатель шахтной подъемной машины |
1 000 000...5 000 000 |
| Электродвигатели прокатного стана |
6 000 000…9 000 000 |
ru.wikipedia.org>
Мощность в цепях переменного тока
В цепях переменного тока различают три вида мощностей: активную Р, реактивную Q и полную S.
Активная мощность вычисляется по формуле:
(2.20) Активную мощность потребляет резистивный элемент. Единица
измерения активной мощности называется Ватт (Вт), производная единица – килоВатт (кВт), равная 103 Вт.
Реактивная мощностьвычисляется по формуле:
(2.21) Реактивная мощность потребляется идеальным индуктивным и
емкостным элементами. Единица измерения реактивной мощности называется Вольт-Ампер реактивный (Вар), производная единица – килоВАр (кВАр), равная 103 ВАр.
Полная мощность потребляется полным сопротивлением и обозначается буквой S:
S=
(2.22) Единица измерения полной мощности называется ВА (Вольт-Ампер), производная единица – килоВольт-Ампер (кВА), равная 103 ВА.
По сути, размерность у всех выше перечисленных единиц измерения одинакова –
. Разные название этих единиц нужны, чтобы различать эти виды мощности. Проявляются различные виды мощности по-разному. Активная мощность необратимо преобразуется в другие виды мощности (например, тепловую, механическую). Реактивная мощность обратимо циркулирует в электрических цепях: энергия электрического поля конденсатора преобразуется в энергию магнитного поля, и наоборот. «Извлечь» реактивную мощность с «пользой для дела» невозможно.
Из формул (2.19) – (2.21) следует, что между активной, реактивной и полной мощностью имеет место соотношение:
(2.23) Соотношение между P, Q и S можно интерпретировать как соотношение сторон прямоугольного треугольника (вспомните треугольник сопротивлений, треугольник напряжений – все эти треугольники подобны).
Рис. 2.10
Из рис. 2.10 видно, что cosφ =
(2.24) Отсюда вытекает определение одной из основных характеристик цепей переменного тока – коэффициента мощности.Специального обозначения он не получил.
Коэффициент мощности показывает, какую долю полной мощности составляет активная мощность.
Желательно, чтобы коэффициент мощности цепи был как можно больше, т.е. приближался к 1. Реально предприятия электрических сетей устанавливают такое ограничение для промышленных предприятий : соs φ = (0,92…..0,95). Достигать значений соs φ >0,95 рискованно, так как разность фаз φ при этом может скачком перейти от положительных значений к отрицательным, что вредно для электрооборудования. Если соsφ < 0,92, предприятия подвергаются штрафу.
Если коэффициент мощности оказывается мал, его необходимо повышать. График функции соs φ имеет вид монотонно убывающей функции в интервале от 00 до 900. Следовательно, увеличить соsφ – значит уменьшить разность фаз
, то есть уменьшить (ХL-ХС). Если влиять на (ХL-ХС), меняя С и L, то это приведет к увеличению тока в последовательной цепи и изменению режима работы оборудования, поэтому такой способ практически не применяется. В следующем разделе рассмотрен другой способ повышения коэффициента мощности.
ЛЕКЦИЯ 4.
2.6 Цепь переменного тока с параллельным соединением ветвей.
Рассмотрим электрическую цепь с двумя параллельными
ветвями (рис. 2.11). Полученные выводы распространим на цепь с любым количеством ветвей. К цепи, содержащей две параллельные ветви, включающие активные, индуктивные и емкостные элементы (R1, L1, C1 и R2, L2, C2 cоответственно), подводится переменное напряжение U частоты f.
Прямая задача: Заданы все Обратная задача: Заданы свойства
входящие в цепь элементы. цепи. Найти неизвестные элементы
Найти все токи и разности цепи (эта задача решена в лабора-
фаз. торной работе Ц-5)
Решим прямую задачу, то есть найдем токи I1, I2 и общий ток I .
Рис. 2.11.Электрическая цепь с двумя параллельными
ветвями
Из второго закона Кирхгофа следует, что напряжения на параллельных участках цепи одинаковы :
U1 = U2 = U (2.25)
На основании закона Ома найдем токи I1 и I2 :
; (2.26) Найдем также разности фаз тока и напряжения для каждой ветви:
(2.27) На основании первого закона Кирхгофа применительно к узлу А можно записать:
= + (2.28) Таким образом, для определения тока I необходимо векторно сложить токи I1 и I2. В качестве опорного вектора удобно выбрать вектор напряжения
. Предположим, что при расчете разностей фаз тока и напряжения в ветвях цепи оказалось, что φ1>0, а φ2
под углом φ1 к вектору , и вектор под углом φ2 к вектору . Графически складываем эти векторы (см. рис.2.12). Величина тока определяется длиной полученного вектора с учетом выбранного масштаба. Разность фаз неразветвленного участка цепи определяется углом между векторами и Рис. 2.12
studopedia.ru>
10. Работа и мощность электрического тока.
Работа электрического тока определяется формулой: A=U*I*t (1.11)
Работу, совершаемую в единицу времени называют мощностью:
P=A/t=U*I (1.12)
Если напряжение U измеряется в вольтах, сила тока I - в амперах, то мощность будет измеряться в ваттах.
1Вт=1В*1А;
Используя закон Ома, вместо уравнения (1.12) для определения мощности можно получить и другие формулы.
P=U*I=U^2/R (1.13)
P=I^2*R (1.14)
Эти формулы используются для определения мощности на участке цепи с заданным сопротивлением R, если на этом участке известно напряжение или протекающий ток.
11. Переменный электрический ток и его основные параметры: период, частота, амплитуда, мгновенное и среднее (действующее) значения.
Переменным называют такой ток, сила и направление которого изменяются периодически. Характерным примером переменного тока является ток синусоидальной формы. Естественно, что в цепях переменного тока напряжения на ее участках также являются переменными.
Основными параметрами, определяющими характер изменения переменного тока, являются период, частота и амплитуда.
Под периодом (Т) понимают время, в течение которого происходит полный цикл изменений переменного тока или одно полное его колебание. Число полных изменений за 1 секунду называют частотой (
) переменного тока или частотой колебаний. Период и частота связаны между собой такой зависимостью: T=1/
(1.15) Период измеряется в секундах или их долях миллисекундах (мс)
1с=10^3мс=10^6мкс=10^9нс=10^12пс;
Частота измеряется в герцах (Гц)
Частота в 1 Гц соответствует одному полному колебанию в секунду. Если за одну секунду происходит 10 полных колебаний , частота такого тока (напряжения) равна 10 Гц, а период Т=0,1с. Переменный ток, применяемый в промышленности, имеет частоту
=50Гц, что соответствует периоду Т=0,02с=20мс, и называется током промышленной частоты. Кроме того по частоте колебаний различают переменные токи (напряжения) низкой (звуковой), средней, высокой и сверхвысокой частоты. Амплитудами переменного тока (Im) и напряжения (Um) называют наибольшие их отношения от нулевого значения. За один период переменные ток и напряжения дважды достигают своего наибольшего значения (рис 1) в течение отрицательного и положительного полупериодов.
Кроме амплитудного переменные токи и напряжения характеризуются мгновенными и действующими значениями.
Мгновенными значениями называют значения тока и напряжения в любой момент времени. Их обозначают строчными буквами i и u. Мгновенные значения синусоидальных тока и напряжения можно выразить через их амплитуду и угловую скорость :
i=Imsin
t; u=Umsin t; Угловая скорость связана с частотой
и периодом T зависимостью:=2=2/T; Коэффициент
соответствует 180^о , т.е. половине длины окружности. Под действующим (эффективным) значением переменного тока понимают величину, равную силе постоянного тока, при протекании которого через проводник в нем выделяется такое же количество тепла, которое выделяет переменный ток за то же самое время. Оно связано с амплитудным значением зависимостью: Im=
I=1,41*I Рис. 1
StudFiles.ru>
Работа и мощность тока (формулировка и формула)????
Никита малахов
Формулировка:
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Формула:
A= U*I*t
1 Джоуль = 1 Вольт * 1 Ампер * 1 секунда
______
Формулировка:
Мощность электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока.
Формула:
P=UI
1 Ватт = 1 Вольт * 1 Ампер
Маша **********
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt,
где U = Δφ12 – напряжение. Эту работу называют работой электрического тока.
Если обе части формулы
RI = U,
выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение
R I2 Δt = U I Δt = ΔA.
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
ΔQ = ΔA = R I2 Δt.
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
Работа электрического тока в СИ выражается в джоулях (Дж) , мощность – в ваттах (Вт).
Читайте также
zna4enie.ru
Работа и мощность переменного тока
Мгновенная мощность в цепи переменного тока (частный случай)
Допустим, что цепь имеет только активное сопротивление. Пусть напряжение на концах цепи изменяется по гармоническому закону:
Мы помним, что сдвига фаз между током и напряжением в нашей цепи (только $R$) не будет, следовательно, запишем, что:
Если рассмотреть маленький промежуток времени, то переменный ток можно рассмотреть как постоянный, значит мгновенная мощность переменного тока ($P_{tR}$) равна:
Работа в цепи переменного тока (частный случай)
Работа переменного тока на маленький промежуток времени $dt$ равна (${dA}_t$):
Следовательно, работа за один период полного колебания ($A_T$) может быть определена как:
Рассмотрим общий случай цепи переменного напряжения, когда она содержит и активное и реактивное сопротивление. Теперь между током и напряжением существует разность фаз. Работа, совершенная во внешней цепи за время $dt$, равна:
Напряжение $U$, можно разложить на две составляющие: активную ($U_a$) и реактивную ($U_r$).
Активная составляющая совершает колебания в одной фазе с током, она равна:
Реактивная составляющая смещена по фазе относительно тока на $\pm \frac{\pi }{2}$ и имеет вид:
При вычислении работы за период, получится два слагаемых. Учитывая, что реактивная составляющая за полный период равна нулю, следовательно, полная работа определена только активной составляющей напряжения:
Средняя мощность
Чаще, чем понятием мгновенная мощность, оперируют понятием среднее значение мощности. Причем рассматривают большой промежуток времени, который включает множество периодов колебаний. Так как мы рассматривает периодический процесс, то нам будет достаточно найти среднее значение мощности на один полный период.
Ее легко найти как:
где $cos\varphi $- коэффициент мощности. Формула (10) показывает, что в общем случае выделяемая в цепи мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между ними.
Замечание
Зависимость мощности от коэффициента мощности учитывают при проектировании линий электропередачи для переменного тока. Если нагрузки вцепи имеют большое реактивное сопротивление, то $\varphi \ne 0$ и $cos\varphi $ может быть заметно меньше единицы. В таких случаях для передачи нужной мощности необходимо учесть силу тока, что ведет к возрастанию выделения тепла Джоуля -- Ленца или требует увеличения сечения проводов, что увеличивает стоимость линии электропередач. На практике всегда стремятся распределить нагрузки так, чтобы $cos\varphi \ $был как можно ближе к единице.
Средняя мощность при наличии в цепи только активного сопротивления, равна:
Пример 1
Задание: Пусть сила тока изменяется в соответствии с законом: $I=I_m{sin \left(\omega t\right)\ }.$ Запишите выражения для мгновенных мощностей, развиваемых током на разных элементах цепи ($C,L$).
Решение:
Используя соотношение:
\[U=\frac{q}{C}(1.1)\] и выражение:
\[I=\frac{dq}{dt}\to q=\int{Idt}=-\frac{I_m}{\omega }{cos \left(\omega t\right)\ }+q_0=-\frac{I_m}{\omega }{cos \left(\omega t\right)\ }\left(1.2\right),\] где мы можем положить $q_0=0,$ так как эта постоянная интегрирования с колебаниями тока не связана, запишем уравнение для колебания напряжения на конденсаторе:
\[U_C=-\frac{I_m}{C\omega }{cos \left(\omega t\right)\ }=\frac{I_m}{C\omega }{sin \left(\omega t-\frac{\pi }{2}\right)\ }\left(1.3\right).\] Мгновенная мощность на конденсаторе равна:
\[P_{tC}=U_CI=\frac{I_m}{C\omega }{sin \left(\omega t-\frac{\pi }{2}\right)\ }\ I_m{sin \left(\omega t\right)\ }=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)\ }\ }.\] Изменение напряжения на индуктивности выразим как:
\[U_L=L\frac{dI}{dt}=LI_m\omega {cos \left(\omega t\right)\left(1.5\right).\ }\] Мгновенная мощность тока на индуктивности:
\[P_{tL}=U_LI=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)\ }.\ }\] Мгновенные мощности на емкости и индуктивности меняют знак. Часть времени ток совершает положительную работу, то есть передает энергию на элементы, другая часть времени работа отрицательна, то есть энергия этих элементов возвращается к источнику сторонних ЭДС. Происходит обмен энергиями между индуктивностями, емкостями и источниками ЭДС в процессе которого емкости и индуктивности выполнят роль источников ЭДС.
Ответ: $P_{tC}=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)\ }\ },$ $P_{tL}=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)\ }.\ }$
Пример 2
Задание: Чему равна средняя мощность на сопротивлении, емкости и индуктивности?
Решение:
Для того чтобы получить средние мощности тока за период колебаний необходимо усреднить выражения:
\[P_{tC}=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)(2.1)\ }\ },\] \[P_{tR}={I^2}_mR{sin}^2\left(\omega t\right)\left(2.2\right),\] \[P_{tL}=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)(2.3)\ }.\ }\] Учтем, что за период колебаний выполняются соотношения:
\[\left\langle {cos \left(\omega t\right){sin \left(\omega t\right)\ }\ }\right\rangle =0\ \left(2.4\right).\] \[\left\langle {s{in}^2 \left(\omega t\right)\ }\right\rangle =\frac{1}{2}\left(2.5\right).\] Используя (2.5) и (2.4) из (2.1) -- (2.2) получим:
\[\left\langle P_{tC}\right\rangle =0,\] \[\left\langle P_{tL}\right\rangle =0,\] \[\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR.\] Ответ: $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR.$
spravochnick.ru
Работа и мощность переменного тока — Мегаобучалка
Энергия, поставляемая источником электродвижущей силы во внешнюю цепь, испытывает превращения в другие виды энергии. Если в цепи имеется только активное сопротивление, то вся энергия превращается в тепло, выделяемое на сопротивлении . Между током и напряжением сдвиг фаз отсутствует. Кроме того, в течение малого промежутка времени переменный ток можно рассматривать как постоянный. Поэтому мгновенная мощность, развиваемая переменным током на сопротивлении:
Хотя ток и напряжение бывают как положительными, так и отрицательными, мощность, равная их произведению, всегда положительна. Однако она пульсирует, изменяясь от нуля до максимального значения с частотой, равной удвоенной частоте переменного тока. На рис. 7.12 показана временная зависимость тока, напряжения и мощности переменного тока, выделяемой на активном сопротивлении. Ясно, что средняя передаваемая мощность меньше максимальной и равна половине максимальной мощности. Среднее значение и за период равно . Это можно объяснить следующим образом: , а за полный цикл среднее значение равно среднему значению . Поэтому среднее значение мощности будет равно
В общем случае, когда цепь содержит не только активное сопротивление, но и индуктивность и емкость, между током и напряжением существует сдвиг фаз, и это сказывается на величине мощности. В цепи с индуктивностью энергия источника переходит в энергию магнитного поля, равную , изменяющуюся с течением времени. Мощность, которая требуется для создания магнитного поля в катушке индуктивности, равна произведению силы тока и разности потенциалов на катушке:
.
Из последней формулы видно, что в том интервале времени, когда , мощность положительна. Это означает, что источник передает энергию во внешнюю цепь, она идет на увеличение энергии магнитного поля. Когда же , мощность отрицательна, в эти промежутки времени энергия, запасенная в магнитном поле, возвращается из внешней цепи в источник. Таким образом, в цепи, содержащей индуктивность, знак мощности периодически изменяется. Так же будет и в случае, когда внешняя цепь содержит конденсатор емкостью . Однако в этом случае происходит переход энергии источника в энергию электрического поля конденсатора, равную . Развиваемая мощность также меняет знак в зависимости от знака .
В катушке индуктивности с нулевым активным сопротивлением или в конденсаторе напряжение сдвинуто по фазе на относительно тока, и поэтому энергия вообще не поглощается. Например, как видно из рис. 7.13, мгновенная мощность в чисто емкостном сопротивлении колеблется между положительными и отрицательными значениями, что соответствует поглощению мощности и затем возвращению ее к источнику. В результате средняя мощность за период равна нулю.
В общем случае полная мощность, развиваемая источником сторонних сил, равна . Эту величину называют мощностью тока, а величины , , – мощностями тока на сопротивлении, индуктивности и емкости соответственно. При силе тока падение напряжения на активном сопротивлении равно , падение напряжения на индуктивности – , падение напряжения на емкости – . Мгновенные значения мощностей соответственно равны
Интерес представляет среднее значение мощности за период. Так как синус и косинус сдвинуты относительно друг друга по фазе на , то среднее значение их произведения равно нулю: . Средние значения квадратов синуса и косинуса . Поэтому , , . Таким образом, отлична от нуля только средняя мощность на активном сопротивлении R, поэтому его и называют активным сопротивлением. На индуктивности и емкости средние мощности равны нулю. Эти элементы в среднем энергетически нейтральны, их называют реактивными сопротивлениями.
megaobuchalka.ru
5. Работа и мощность в цепи переменного тока
Мгновенное значение мощности р(t) переменного тока равно произведению мгновенных значений напряжения u(t) =U0cosωtи силы токаi(t) = I0cos(ωt– φ):
р(t) = U0cosωtI0 cos(ωt – 900) = I0U0 cosωt cos(ωt – 900).()
Воспользовавшись формулой получим:.
Практический интерес представляет среднее по времени значение мощности Р. Т.к. среднее значение cos(2ωt- φ) равно нулю, то
. ()
Из векторной диаграммы рис. 7б следует, что U0 cosφ= RI0. Поэтому. Такую же мощность развивает постоянный ток, силой. Это значение называется действующим (или эффективным) значением силы переменного тока. Аналогично величинаназывается действующим (или эффективным) значением напряжения. С использованием действующих (или эффективных) значений тока и напряжения Р =U0 I0cosφ.Множительcosφназывается коэффициентом мощности. Как видно из диаграммы рис. 7б, при равенстве реактивных значений сопротивлений ХC= ХLмножительcosφ= 1 (φ = 0) Р =U0 I0, т.е. выделяющаяся в цепи мощность имеет максимальное значение. При чисто реактивном сопротивлении цепи (R= 0) мощность, выделяемая в цепи, равна нулю. По этой причине на практике электрическую цепь переменного тока стремятся сбалансировать так чтобы значения реактивных сопротивлений ХCи ХLбыли как можно ближе. Для промышленных установок наименьшее допустимое значениеcosφ= 0,85.
или. (48)
Работа за период T:. (49)
Средняя мощность переменного тока . (50)
Обозначим , откуда эффективный (действующий) ток -. (51)
Тогда . (52)
Из сравнения соотношений (47) и (52) следует, что эффективная сила переменного равна силе такого постоянного тока, который имеет ту же мощность, что и данный переменный ток.
Если в цепи переменного тока имеются реактивные сопротивления, то мощность:
(53)
(на основании тригонометрического тождества: ).
Среднее значение мощности NСза период Т, а, следовательно, и за любой промежуток времениt>>T, равно разности средних значений. Но первый член есть постоянная величина, не зависящая от времени, а второй – периодическая функция, среднее значение которой за периодTравна нулю. Таким образом,(54)
или (55)
Множитель называется коэффициентом мощности электрической цепи. ЕслиR=0, тоиNC=0. Энергия, которая поступает в цепь от источника за T/2, возвращается источнику в течение следующей половины периода. Следовательно, для повышения мощности, отдаваемой переменным током в цепь, необходимо добиться повышенияпутём включения в цепь такихRLиRCнагрузок, которые соответствуют условию резонанса (45).
6. Природа емкостных свойств тканей организма
ИМПЕДАНС БИОЛОГИЧЕСКИХ ТКАНЕЙ
Метод электропроводности в медицине
Как показывает опыт, электропроводность растворов не зависит от частоты переменного тока. При изучении электропроводности биологических объектов обнаружили, что их сопротивление на высоких частотах (~107 Гц) гораздо меньше, чем на низких. На рис.9 (кривая 1) представлена зависимость сопротивления мышечной ткани от частоты (кривая дисперсии). Дисперсия электропроводности обычно наблюдается в интервале частот 102 ÷ 108 Гц. Наличие дисперсии импеданса для живых тканей обусловлено тем, что при низких частотах (как и для постоянного тока) на величину электропроводности значительное влияние оказывает макроструктурная поляризация в тканях. По мере увеличения частоты поляризационные явления сказываются всё меньше и меньше.
Отмирание ткани ведёт к росту проницаемости мембран, при этом крутизна дисперсии уменьшается (рис.9, кривая 2). Для мёртвой ткани поляризация на границах раздела практически полностью исчезает и явление дисперсии импеданса больше не наблюдается (рис.9, кривая 3). Т.о. крутизна графика зависимости Z = f(ω) позволяет судить о жизнеспособности той или иной ткани.
Наличие дисперсии электропроводности говорит о том, что в биологических объектах наряду со структурами, которые оказывают переменному току активное сопротивление, есть и такие, которые обладают реактивным сопротивлением. Как оказалось, структуры с индуктивным сопротивлением (подобные катушкам) в биологических организмах отсутствуют.
Клеточные мембраны, омываемые с одной стороны тканевой жидкостью, а с другой цитоплазмой, представляют собой системы подобные конденсатору. В тканях имеются так же макроскопические образования, состоящие из различных непроводящих соединительных оболочек и перегородок, по обе стороны которых находятся ткани, хорошо проводящие электрический ток. Это так же придаёт тканям емкостные свойства.
В целом, сопротивление биологических тканей будет определяться суммой омического и емкостного сопротивления:
. (12)
Присутствие в биологических организмах структур с ёмкостным сопротивлением подтверждается также наличием сдвига фаз между током и напряжением. Для биологических систем характерна большая величина этого угла, например, на частоте 1000 Гц: кожа человека – φ = 550, мышца кролика – φ = 650, нерв лягушки – φ = 640. Это показывает, что доля емкостного сопротивления в импедансе тканей велика.
При моделировании электропроводности живых клеток и тканей прибегают к эквивалентным схемам, т.е. к таким комбинациям омического сопротивления и ёмкости, которые в некотором приближении могут отражать характер течения тока и значения электрических параметров клетки и тканей. Простейшими из таких моделей являются схемы с последовательным и с параллельным соединением R и C – (рис.10а и 11а). Но эти простейшие схемы не отражают истинного положения дел, т.к. графики зависимости Z от ω противоречат данным по живым тканям (сравните рис.10б, 11б и рис.6, кривая1).
Наиболее удачной моделью является схема, представленная на рис.12а. На этой схеме Rк,1 и Rк,2 – активные сопротивления кожи на входе и выходе тока; Rт – общее омическое сопротивление подкожных тканей; C1, C2 и C3 – конденсаторы, моделирующие биологические структуры, обладающие ёмкостным сопротивлением. Стрелками показан маршрут переменного тока, т.е. показаны структуры, через которые проходит ток на каждом из участков биологического организма между электродами за один полупериод. Зависимость сопротивления этой эквивалентной схемы от частоты хорошо согласуется с кривой дисперсии импеданса для биотканей (рис.12б) Существуют и другие эквивалентные схемы, однако ниодна из них в точности не может воспроизвести закономерности течения переменного тока, присущие биологическим системам.
Измерение электропроводности биологических тканей для переменного тока широко используется в диагностике, а так же в биологических и медицинских исследованиях. Например, значительное возрастанию импеданса ткани на низких частотах позволяет обнаружить воспаление уже на первых стадиях. Некоторые заболевания щитовидной железы диагностируются по изменению угла сдвига фаз между током и напряжением. Для характеристики физиологического состояния тканей используют также величину крутизны кривой дисперсии. Этот критерий применяют, например, при оценке жизнеспособности ткани, предназначенной для трансплантации.
Импеданс тканей существенным образом зависит от кровенаполнения сосудов. Кровь имеет меньшее сопротивление, чем стенки сосудов или клетки, поэтому во время систолы полное сопротивление ткани уменьшается, а при диастоле – увеличивается. Диагностический метод, основанный на регистрации импеданса тканей в процессе сердечной деятельности, называется реографией (импеданс – плетизмографией). С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), лёгких, печени, сосудов, конечностей. Измерения обычно проводят на частоте 30 кГц.
studfiles.net
Работа и мощность переменного тока
34.Работа и мощность переменного тока.
Работа основана на явлении электромагнитной индукции.
Полная мощность генератора переменного тока определяется произведением тока на напряжение:
S=UI
где S — полная мощность, ва;
I — действующая сила тока, на которую рассчитана обмотка генератора, а;
U – расчетное действующее значение напряжения генератора, в.
Размеры генератора переменного тока зависят от полной мощности, на которую он рассчитывается. Это связано с тем, что поперечное сечение проводов обмотки определяется силой тока, а толщина изоляции и число витков обмотки — напряжением, которое будет вырабатывать генератор.
Полная мощность генератора переменного тока, включенного в цепь с активным (г) и реактивными сопротивлениями (ХL и Хс), состоит из мощности, расходуемой в активном сопротивлении, и реактивной части мощности.
Мощность, расходуемая в активном сопротивлении, преобразуется в полезную работу или тепло, рассеиваемое в пространство

Реактивная часть мощности обусловлена колебаниями энергии при создании и исчезновении магнитных и электрических полей. Энергия то запасается в полях реактивных сопротивлений, то возвращается генератору, включенному в цепь. Реактивные токи, протекающие между генератором и реактивными приемниками, обладающими индуктивным и емкостным сопротивлениями, бесполезно загружают линию и генератор и этим вызывают дополнительные потери энергии.
Связь между полной, активной и реактивной мощностями определим из треугольника мощностей. Для построения треугольника мощности умножим стороны треугольника напряжений (рис. 62, а) на силу тока I, тогда получим подобный треугольник мощностей А'О'Б' (рис. 62,6). Сторона О'Б' этого треугольника равна активной мощности Р, сторона Б'А' — реактивной мощности Q, а гипотенуза А'О' треугольника равна полной мощности S.
Из треугольника мощностей следует, что отношение

Отсюда активная мощность Р=S cos j. Так как полная мощность генератора переменного тока S=UI, то активная мощность определяется так:  измеряется в ваттах. Из этого же треугольника следует, что отношение
измеряется в ваттах. Из этого же треугольника следует, что отношение 
Отсюда реактивная мощность  и измеряется в вольт-амперах реактивных (вар). Полная мощность
и измеряется в вольт-амперах реактивных (вар). Полная мощность  измеряется в вольт-амперах (ва).
измеряется в вольт-амперах (ва).
Чтобы судить о том, какая часть полной мощности расходуется как активная (полезная) мощность и какая часть является реактивной (бесполезной) мощностью, следует разделить активную мощность на полную. Из треугольника мощностей видно, что это отношение характеризуется косинусом угла сдвига фаз между током и напряжением в данной цепи: 
Таким образом, cos j является коэффициентом мощности переменного тока.
Пример. Полная мощность установки S = 800 ва. Ваттметр, измеряющий активную часть мощности, показывает что она равна 720 вт. Определить коэффициент мощности.
Р е ш е н и е. Коэффициент мощности 
Это значит, что 90% полной мощности расходуется в виде активной мощности на полезную работу, а 10% обусловлены наличием реактивной бесполезной мощности.
В цепи переменного тока с активным сопротивлением ток и напряжение совпадают по фазе и угол сдвига фаз равен нулю. Так как cos j=1, то активная мощность для такой цепи Р=IU, т. е, равна полной мощности. В данном случае вся мощность генератора используется для полезной работы.
Угол сдвига фаз между током и напряжением зависит от соотношения между активным и реактивным сопротивлениями, включенными в цепь.Увеличение активного сопротивления приводит к уменьшению угла сдвига фаз, а следовательно, к возрастанию косинуса этого угля и к увеличению коэффициента мощности. Индуктивная нагрузка, подключенная в цепь, наоборот, увеличивает угол сдвига фаз и тем самым понижает коэффициент мощности.Причиной низкого коэффициента мощности может быть работал электродвигателей станков или машин вхолостую; недогрузка станка, связанная с тем, что на станке большой мощности обрабатываются мелкие детали; неправильный выбор мощности двигателя, устанавливаемого на станке; низкое качество ремонта двигателя; плохая смазка и т. д. При нормальной нагрузке двигателя его коэффициент мощности составляет 0,83—0,85. При холостом ходе двигателя его коэффициент мощности понижается и составляет 0,1—0,3.Это значит, что активная мощность мала. Для повышения коэффициента мощности параллельно к индуктивной нагрузке предприятия подключают конденсаторы. Емкостное сопротивление этих конденсаторов подбирают с таким расчетом, чтобы оно было примерно равно индуктивному. При этом емкостный ток будет также примерло равен индуктивному току. В этом случае угол сдвига фаз между током и напряжением уменьшается, коэффициент мощности возрастает до 0,85—0,9.Установлено, что повышение коэффициента мощности в энергосистемах нашей страны только на 0,01 может дать ежегодно экономию более 500 млн. квт×ч электрической энергии.
Таким образом, повышение коэффициента мощности и экономное расходование электрической энергии — важное государственное дело.
studlib.info
РАБОТА И МОЩНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА. ПОНЯТИЕ КОЭФФИЦИЕНТА МОЩНОСТИ.
Понятие потенциала или разности потенциалов u позволяет определить работу, совершаемую электрическим полем при перемещении элементарного электрического заряда dq, как dA = udq. В то же время, электрический ток равен i = dq/dt. Отсюда dA = ui dt, следовательно, скорость совершения работы, т.е. мощность в данный момент времени или мгновенная мощность равна
 ,
,
где u и i - мгновенные значения напряжения и тока.
Величины тока и напряжения, входящие в выражение (1), являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной и для ее оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период T работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т.е.
 .
.
Пусть u=Umsinw t и Imsin(wt-j ), тогда средняя мощность будет равна
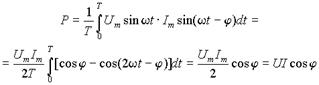
т.к. интеграл второго слагаемого равен нулю. Величина cosj называется коэффициентом мощности.
Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока I и напряжения U, но и от разности фаз j между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению UI. При сдвиге фаз между током и напряжением в ± 90° средняя мощность равна нулю. Максимальные значения напряжения и тока любой электрической машины определяются ее конструкцией, а максимальная мощность, которую они могут развивать - произведением этих величин. Если электрическая цепь построена нерационально, т.е. сдвиг фаз j имеет значительную величину, то источник электрической энергии и нагрузка не могут работать на полную мощность. Поэтому в любой системе источник-нагрузка существует т.н.
"проблема cosj" , которая заключается в требовании возможного приближения cos j к единице.
Выражение (3) можно представить также с помощью понятий активных составляющих тока Iа и напряжения Uа в виде
P = UI cosj = U(I cosj ) = UIа = I(U cosj ) = IUа.
Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как Iа=U/R или Uа=IR , выражение (4) можно записать также в форме
P = I2R = U2/R.
Среднюю мощность P называют также активной мощностью и измеряют в ваттах [Вт].
Выделим подинтегральную функцию выражения (3)

Отсюда следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей UIcosj равной средней или активной мощности.
При cosj = 1 (j = 0) , т.е. для цепи, обладающей чисто резистивным сопротивлением
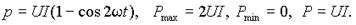
Временные диаграммы, соответствующие этому случаю приведены на рис. 1 а).

Положительные значения мгновенной мощности соответствуют поступлению энергии от источника в электрическую цепь. Следовательно, при резистивной нагрузке вся энергия поступающая от источника преобразуется в ней в тепло.
При cosj = 0 (j = ± p /2) , т.е. для чисто реактивной цепи

Временные диаграммы, соответствующие чисто индуктивной и чисто емкостной нагрузке приведены на рис. 1 б) и г). Из выражений (8) и временных диаграмм следует, что мощность колеблется относительно оси абсцисс с двойной частотой, изменяя свой знак каждые четверть периода. Это означает, что в течение четверти периода (p > 0) энергия поступает в электрическую цепь от источника и запасается в магнитном или электрическом поле, а в течение следующей четверти (p < 0) она целиком возвращается из цепи в источник. Так как площади, ограниченные участками с положительной мощностью и с отрицательной одинаковы, то средняя мощность отдаваемая источником нагрузке равна нулю и в цепи не происходит преобразования энергии.
В общем случае произвольной нагрузки 1 > cosj > 0 ( 1< |j | < p /2) и
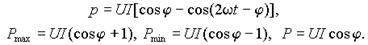
Как следует из временных диаграмм рис. 1 в), большую часть периода мощность потребляется нагрузкой (p > 0), но существуют также интервалы времени, когда энергия запасенная в магнитных и электрических полях нагрузки возвращается в источник. Участки с положительным значением p независимо от характера реактивной составляющей нагрузки всегда больше участков с отрицательным значением, поэтому средняя мощность P положительна. Это означает, что в электрической цепи преобладает процесс преобразования электрической энергии в тепло или механическую работу.
Рассмотрим энергетические процессы в последовательном соединении rLC (рис. 2). Падение напряжения на входе цепи уравновешивается суммой падений напряжения на элементах u=ur+uL+uC . Мгновенная мощность в цепи равна
ui=uri+uLi+uCi

xCImsin(wt-j -p /2). Подставляя эти выражения в (9), получим

Уравнение (10) в левой и правой частях имеет постоянную и переменную составляющие. Постоянная составляющая представляет собой активную или среднюю мощность. Второе слагаемое в правой части это переменная составляющая активной мощности с амплитудой равной P = UIcosj . Третье слагаемое правой части также является переменной составляющей мгновенной мощности, но эта составляющая находится в квадратуре с переменной составляющей активной мощности и имеет амплитуду Q = UIsinj . Эту величину называют реактивной мощностью. Она равна среднему за четверть периода значению энергии, которой источник обменивается с магнитным и электрическим полями нагрузки. Реактивная мощность не преобразуется в тепло или другие виды энергии, т.к. ее среднее значение за период равно нулю.
Реактивную мощность также можно представить через реактивные составляющие тока или напряжения
Q = UI sinj = U(I sinj ) = UIр = I(U sinj ) = IUр.
В отличие от всегда положительной активной мощности, реактивная мощность положительна при j > 0 и отрицательна при j < 0 .
Из условия равенства переменных составляющих левой и правой частей уравнения (10) можно найти связь между P, Q и S = UI в виде

Величина S называется полной или кажущейся мощностью. Из выражения (12) следует, что полную мощность можно представить гипотенузой прямоугольного треугольника с углом j , катетами которого являются активная и реактивная мощности.
Таким образом, полная мощность это максимально возможная активная мощность, т.е. мощность, выделяющаяся в чисто резистивной нагрузке (cosj = 0). Именно эта мощность указывается в паспортных данных электрических машин и аппаратов.
Реактивные составляющие токов и напряжений можно представить через активные и реактивные составляющие комплексного сопротивления, тогда для составляющих мощности
P = UIа = I2R = UаI = U2/R = U2G ;
Q = UIр = I2X = UрI = U2/X = U2B ;
S = UI = I2Z = U2/Z = U2Y.
Треугольник мощностей можно описать также с помощью комплексных чисел и изобразить векторами на комплексной плоскости в виде
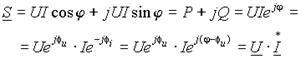 ,
,
 где S - комплексная полная мощность,
где S - комплексная полная мощность,  - сопряженный комплексный ток.
- сопряженный комплексный ток.
Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4) и (11)), треугольник мощностей можно построить в двух вариантах (рис. 3 а) и б)). В первом случае активная и реактивная составляющие полной мощности выражаются  через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I.
через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I.
Очевидно, что все виды мощности имеют одинаковую размерность, поэтому для их отличия от активной мощности, измеряемой в ваттах [Вт], для полной мощности введена единица, называемая вольт-амперы [ВА], а для реактивной мощности - вольт-амперы реактивные [ВАр]
Выражение для активной мощности P = UIcosj позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.
Для этого на вход цепи включают приборы по схеме рис. 4 и по их показаниям определяют коэффициент мощности в виде
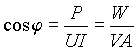 ,
,
где W, V и A - показания соответственно ваттметра, вольтметра и амперметра действующих значений. Из этого выражения можно также определить угол сдвига фаз j между током и напряжением на входе двухполюсника.
lektsia.com
Работа и мощность переменного тока. Действующее значение тока и напряжения.
Найдем мощность, выделяемую в цепи переменного тока. Мгновенное значение мощности равно произведению мгновенных значений напряжения и силы тока:
 ***Воспользуемся формулой :
***Воспользуемся формулой :

Выражению *** можно придать вид:
 **
**
Практический интерес представляет среднее по времени значение Р(t), которое мы обозначим просто Р. Так как среднее значение 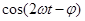 равно нулю,
равно нулю,
 *
*
Из * *следует , что мгновенная мощность колеблется около среднего значения с частотой, в 2 раза превышающую частоту тока.

 Подставив это значение
Подставив это значение 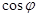 в формулу * и учтя, что
в формулу * и учтя, что  , получим
, получим
Такую же мощность развивает постоянный ток, сила которого равна 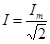 - действующее значение силы тока.
- действующее значение силы тока. 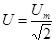 - действующее значение напряжения.
- действующее значение напряжения.
Выражение средней мощности через действующие значения силы тока и напряжения имеет вид 
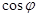 - коэффициент мощности. В технике стремятся сделать
- коэффициент мощности. В технике стремятся сделать 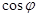 как можно больше. При малом
как можно больше. При малом 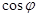 для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.
для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.
Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.
Напряженность электростатического поля. Принцип суперпозиции. Расчет напряженности поля тонкого заряженного стержня.
Электрический диполь и его поле.
Силовые линии электростатического поля. Поток вектора. Электростатическая теорема Гаусса и ее применение для расчета полей.
Работа электростатического поля. Теорема о циркуляции напряженности электростатического поля. Потенциал. Эквипотенциальная поверхность. Связь потенциала с напряженностью.
Проводники в электростатическом поле. Распределение заряда в проводнике. Электростатическое поле в полости.
Поверхностная плотность заряда. Граничные условия на границе проводника с вакуумом.
Дифференциальная форма теоремы Гаусса. Уравнение Пуассона. Общая задача электростатики.
Емкость уединенного проводника. Конденсатор. Емкость конденсаторов различной конфигурации. Соединение конденсаторов.
Энергия конденсатора. Плотность энергии электростатического поля.
Поляризация диэлектриков. Связанные заряды. Вектор поляризации. Диэлектрическая проницаемость.
Теорема Гаусса для электростатических полей в веществе. Электрическое смещение. Граничные условия на границе раздела диэлектриков.
Электрический ток и его характеристики. Условия существования тока. Законы Ома и Джоуля- Ленца в дифференциальной форме.
Сторонние силы. ЭДС. Закон Ома для участка цепи с источником ЭДС. Закон Джоуля-Ленца в интегральной форме.
Правила Кирхгофа и расчет электрических цепей.
Магнитное поле. Сила Лоренца и сила Ампера. Вектор магнитной индукции.
Закон Био-Савара. Принцип суперпозиции. Магнитное поле прямолинейного тока и кругового тока.
Виток с током в магнитном поле. Момент сил, действующих на виток с током в магнитном поле.
Теорема Гаусса для магнитного поля. Закон полного тока. Магнитное поле соленоида.
Магнитная энергия тока. Плотность энергии магнитного поля.
Движение заряженных частиц в электрическом и магнитном полях.
Масс-спектрометр. Принцип работы и применение.
Эффект Холла. Постоянная Холла.
Явление электромагнитной индукции. ЭДС индукции, возникающая в движущихся проводниках. Закон электромагнитной индукции. Правило Ленца.
Явление самоиндукции. Индуктивность. Индуктивность длинного соленоида.
Магнитное поле в веществе. Молекулярные токи. Намагниченность. Магнитная проницаемость.
Пара- и диамагнетики и их свойства. Элементарная теория диамагнетизма.
Ферромагнетики и их свойства.
Максвелловская трактовка закона электромагнитной индукции. Обобщение теоремы о циркуляции
электростатического поля на случай переменных полей.
Ток смещения. Обобщение закона полного тока на случай переменных полей.
Система уравнений Максвелла в интегральной форме. Материальные уравнения. Скорость распространения электромагнитных возмущений.
Скин-эффект и его элементарная теория.
Генератор переменного тока. Емкость, индуктивность и активное сопротивление в цепи переменного тока. Закон Ома для переменных токов.
Затухающие колебания в колебательном контуре. Коэффициент затухания и логарифмический декремент затухания колебаний.
Вынужденные колебания в колебательном контуре. Резонанс.
Работа и мощность переменного тока. Действующее значение тока и напряжения.
infopedia.su


 измеряется в ваттах. Из этого же треугольника следует, что отношение
измеряется в ваттах. Из этого же треугольника следует, что отношение 
 и измеряется в вольт-амперах реактивных (вар). Полная мощность
и измеряется в вольт-амперах реактивных (вар). Полная мощность  измеряется в вольт-амперах (ва).
измеряется в вольт-амперах (ва).

 ,
, .
.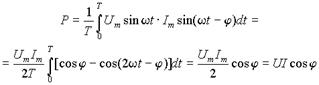

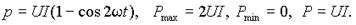


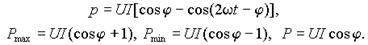



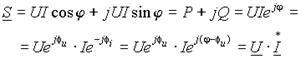 ,
, где S - комплексная полная мощность,
где S - комплексная полная мощность,  - сопряженный комплексный ток.
- сопряженный комплексный ток. через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I.
через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I.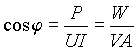 ,
, ***Воспользуемся формулой :
***Воспользуемся формулой :
 **
**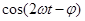 равно нулю,
равно нулю, *
*
 Подставив это значение
Подставив это значение 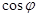 в формулу * и учтя, что
в формулу * и учтя, что  , получим
, получим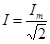 - действующее значение силы тока.
- действующее значение силы тока. 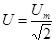 - действующее значение напряжения.
- действующее значение напряжения.
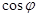 - коэффициент мощности. В технике стремятся сделать
- коэффициент мощности. В технике стремятся сделать 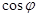 как можно больше. При малом
как можно больше. При малом 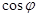 для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.
для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.






Поделиться с друзьями: