5. Делитель напряжения. Схема делителя напряжения
1. Делители напряжения | 5. Схемы делителей и законы Кирхгофа | Часть1
1. Делители напряжения
Делители напряжения
Давайте проанализируем простую последовательную цепь и определим напряжения на каждом из ее резисторов:


Зная сопротивления каждого из резисторов, мы можем вычислить общее сопротивление цепи (которое для последовательной цепи будет равно сумме отдельных сопротивлений):

Теперь, используя закон Ома (I = U/R), определяем общую силу тока, которая будет одинакова на всех компонентах нашей последовательной цепи:

И наконец, зная общую силу тока (2 миллиампера), давайте рассчитаем напряжение на каждом из резисторов:

Из этой таблицы видно, что напряжения на резисторах пропорциональны их сопротивлениям (учитывая, что сила тока через все резисторы одинакова). Заметьте, напряжение на резисторе R2 в два раза больше напряжения на резисторе R1, так же как и сопротивление R2 в два раза больше сопротивления R1.
Если мы изменим общее напряжение цепи, то увидим, что эта пропорциональность сохранится:

Несмотря на увеличение напряжение источника питания, напряжение на резисторе R2 по прежнему в два раза больше напряжения на резисторе R1.
Произведя несколько подобных наблюдений становится очевидным, что напряжение на каждом из резисторов составляет фиксированную пропорцию от общего напряжения. Например, при напряжении батареи 45 вольт, напряжение на резисторе R1 составляло 10 вольт. Когда напряжение батареи было увеличено до 180 вольт (в 4 раза), напряжение на резисторе R1 так же увеличилось в 4 раза (с 10 до 40 вольт). Как видите, соотношение между напряжением на резисторе R1 и общим напряжением не изменилось:

Соотношения других напряжений с увеличением напряжения питания так же не изменятся:

Из за способности последовательной цепи пропорционально распределять общее напряжение по резистивным компонентам, ее часто называют делителем напряжения. Немного поколдовав с математикой, можно получить формулу для определения напряжения на любом резисторе, имея только значения сопротивлений отдельных резисторов, общего напряжения и общего сопротивления:

Полученная нами формула известна как формула делителя напряжения, с ее помощью легче рассчитывать напряжения последовательной цепи, чем производить аналогичные расчеты с использованием закона Ома.
Используя эту формулу можно повторно проанализировать приведенную выше схему, и определить ее напряжения произведя меньшее количество действий:


Делители напряжения нашли широкое применение в схемах измерительных приборов, где определенные комбинации соединенных последовательно резисторов используются для "деления" напряжения на нужные пропорции, необходимые для измерения разных величин того же напряжения.

Одним из устройств, часто используемых в качестве делителя напряжения, является потенциометр. Потенциометр представляет собой проводник с большим омическим сопротивлением (резистор), снабженный скользящим контактом:

Условное обозначение потенциометра представляет собой вертикальный символ резистора с примыкающей к нему стрелкой - скользящим контактом. Если скользящий контакт переместить ближе к контакту 1, то сопротивление между ними будет меньше, чем сопротивление между скользящим контактом и контактом 2. Если скользящий контакт переместить ближе к контакту 2, то эффект будет противоположным. Сопротивление между контактами 1 и 2 будет постоянным, независимо от положения скользящего контакта:

На рисунке ниже показана конструкция двух типов потенциометров, роторного и линейного:


Некоторые линейные потенциометры приводятся в действие посредством прямолинейного движения рычага или слайд-кнопки. Другие, как тот, который изображен на рисунке - посредством отвертки, для более точной настройки. Такие потенциометры называют еще "подстроечными". Следует отметить, что не у всех линейных потенциометров назначение выводов соответствует показанным на рисунке. У некоторых, вывод скользящего контакта находится посередине, между выводами конечных контактов.
На следующей фотографии изображен реальный ротационный потенциометр с открытыми для просмотра скользящим контактом и резистивным элементом. Рукоятка этого потенциометра повернута таким образом, что его скользящий контакт почти касается левого вывода резистивного элемента:

А здесь показан тот же самый потенциометр, но его скользящий контакт повернут против часовой стрелки в другую сторону:

Если постоянное напряжение приложить к контактам резистивного элемента потенциометра, то скользящий контакт выступит в роли своеобразного "крана", с помощью которого можно регулировать величину этого напряжения на выходе прибора:

По аналогии с фиксированным делителем напряжения, пропорциональность деленного потенциометром напряжения является исключительно функцией сопротивления, а не приложенного напряжения. Иными словами, если ручкой потенциометра установить его скользящий контакт строго посередине резистивного элемента, то на выходе мы получим ровно половину от приложенного напряжения, независимо от его величины. Можно сказать, что потенциометр функционирует как регулируемый делитель напряжения, в котором пропорциональность деленного напряжения устанавливается положением скользящего контакта.
Такая функция потенциометра очень полезна для получения регулируемого напряжения от фиксированного источника, например батареи. Если собранная вами схема требует напряжение, которое меньше напряжения имеющейся батареи, то вы можете подключить к этой батарее выводы резистивного элемента потенциометра, и ручкой "выставить" нужное напряжение между скользящим контактом и одним из конечных контактов:

Такое применение потенциометра при проектировании электрических схем пользуется большой популярностью.
На следующей фотографии показаны небольшие потенциометры, которые обычно применяются в бытовых электроприборах и различных радиолюбительских схемах:

Самый левый и самый правый потенциометры могут устанавливаться непосредственно на макетную или печатную плату. Средние устройства предназначены для установки на плоскую панель, со схемой они соединяются при помощи проводов.
Ниже показаны специализированные потенциометры:

www.radiomexanik.spb.ru
Делитель напряжения | Электронные печеньки
Что такое делитель напряжения?
Делитель напряжения — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. Делитель можно представить, как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Чаще всего делитель напряжения строится из двух резисторов. Такой делитель называют резисторным. Каждый резистор в таком делителе называют плечом. Плечо соединённое с землёй называют нижним, то что соединено с плюсом — верхним. Точка соединения двух резисторов называется средним плечом или средней точкой. Если говорить совсем упрощённо, то можно представить среднее плечо, как бассейн. Делитель напряжения позволяет нам управлять двумя «шлюзами», «сливая» напряжение в землю (уменьшая сопротивление нижнего плеча) или «подливая» напряжения в бассейн (уменьшая сопротивление верхнего плеча). Таким образом, делитель может использоваться для того, чтобы получить из исходного напряжения лишь его часть.
Принципиальная схема делителя напряжения
В рассматриваемом примере на вход (Uвх) подаётся напряжение 9В. Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?
Расчёт делителя напряжения
Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.
Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:
Rобщ = R1 + R2 = 400 + 500 = 900 Ом
По закону Ома находим силу тока, протекающего через резисторы:
I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА
Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):
Uвых = I * R2 = 0.01А * 500 Ом = 5В
Или упрощая цепочку вычислений:
Uвых = Uвх * (R2 / (R1+R2))
Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:
R1 = (Uвх-Uвых)/Iд+Iн
R2 = Uвых / Iд
Здесь Iд и Iн — ток делителя и ток нагрузки соответственно. В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд = 0.01 А (10 мА), а Iн = 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:
R1 = (Uвх-Uвых) * 100
R2 = Uвых * 100
P.S. Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель.
Проверяем:
Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:
R1 = (9-5) * 100 = 400 Ом
R2 = 5 * 100 = 500 Ом
Всё сходится!
Применение делителя напряжений
В основном делитель напряжения используется там, где нужно измерить изменяющееся сопротивление. На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.
uscr.ru
Схемы делителей напряжения
При включении по схеме делителя напряжения датчик включается в цепь последовательно с некоторым постоянным сопротивлением 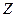 , которое в общем виде может быть комплексным. Добавочным сопротивлением может служить, например, резистор, индуктивность или емкость (см. рис. 4.8.2.1). При питании цепи переменным напряжением, напряжение на датчике, измеряемое вольтметром V того или иного типа, будет зависеть от полного сопротивления датчика. Если соблюдается условие
, которое в общем виде может быть комплексным. Добавочным сопротивлением может служить, например, резистор, индуктивность или емкость (см. рис. 4.8.2.1). При питании цепи переменным напряжением, напряжение на датчике, измеряемое вольтметром V того или иного типа, будет зависеть от полного сопротивления датчика. Если соблюдается условие 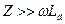 , то
, то
 ,
,
откуда следует, что напряжение на датчике прямо пропорционально величине его индуктивности.
Чувствительность по напряжению схемы
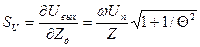 .
.
Выходной сигнал схемы включения при изменении полного сопротивления датчика
 .
.
С другой стороны, выходное напряжение схемы делителя напряжения зависит также от величины напряжения питания  и частоты питающего тока
и частоты питающего тока  . Нетрудно убедиться, что
. Нетрудно убедиться, что  и
и  ; следовательно, стабильность источника питания по частоте и напряжению определяет погрешность преобразования измерительного сигнала схемой делителя напряжения.
; следовательно, стабильность источника питания по частоте и напряжению определяет погрешность преобразования измерительного сигнала схемой делителя напряжения.

Включение дифференциального датчика в схему делителя напряжения показано на рисунке 4.8.2.2. Обмотки датчика 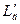 и
и  образуют делитель напряжения, питаемый переменным током.
образуют делитель напряжения, питаемый переменным током.
При изменении индуктивностей обмоток будет изменяться их полное сопротивление и падение напряжения на обмотках. Это падение напряжения выпрямляется диодами  и
и  . Конденсаторы
. Конденсаторы 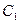 и
и  служат для сглаживания пульсаций выпрямленного напряжения, а резисторы
служат для сглаживания пульсаций выпрямленного напряжения, а резисторы  ,
,  ,
, 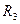 являются сопротивлениями нагрузки для выпрямителей.
являются сопротивлениями нагрузки для выпрямителей.
Показывающий вольтметр V подключен к одноименным полюсам выпрямителей. В этом случае он будет показывать разницу напряжений на обмотках датчика 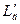 и
и  . Когда индуктивности обмоток равны, равны и их полные сопротивления и падения напряжения на них. Вольтметр при этом покажет нуль. Регулировка нулевых показаний вольтметра при настройке может осуществляться переменным резистором
. Когда индуктивности обмоток равны, равны и их полные сопротивления и падения напряжения на них. Вольтметр при этом покажет нуль. Регулировка нулевых показаний вольтметра при настройке может осуществляться переменным резистором  .
.
Мостовые схемы
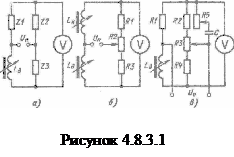
Весьма широкое распространение для включения индуктивных датчиков нашла мостовая схема включения в различных вариантах (см. рис. 4.8.3.1). Общий вид мостовых схем включения недифференциального индуктивного датчика показан на рисунке. Если соблюдается условие
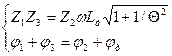
 где
где  – фазовый угол соответствующего комплексного сопротивления, то выходное напряжение
– фазовый угол соответствующего комплексного сопротивления, то выходное напряжение  равно нулю, и мост в этом случае сбалансирован или уравновешен. Условие равновесия мостовой схемы формулируется следующим образом: «для равновесия мостовой схемы необходимо, чтобы произведения модулей комплексных сопротивлений накрест лежащих плеч моста, а также суммы их углов фазовых сдвигов были равны между собой». При изменении индуктивности датчика условие равновесия моста нарушается, и выходное напряжение моста пропорционально изменению индуктивности.
равно нулю, и мост в этом случае сбалансирован или уравновешен. Условие равновесия мостовой схемы формулируется следующим образом: «для равновесия мостовой схемы необходимо, чтобы произведения модулей комплексных сопротивлений накрест лежащих плеч моста, а также суммы их углов фазовых сдвигов были равны между собой». При изменении индуктивности датчика условие равновесия моста нарушается, и выходное напряжение моста пропорционально изменению индуктивности.
Плечи мостовой схемы в общем случае являются комплексными сопротивлениями и в конкретных схемах включения могут быть реализованы включением резисторов, индуктивностей или емкостей. Пример реализации мостовой схемы приведен на рисунке 4.8.3.1 б). Одним плечом моста является индуктивность датчика  , второе плечо – компенсационная индуктивность
, второе плечо – компенсационная индуктивность  , третье и четвертое – образованы резисторами
, третье и четвертое – образованы резисторами  ,
,  и
и  . Для резисторов фазовый угол
. Для резисторов фазовый угол  . Для индуктивностей
. Для индуктивностей  . В связи с этим удается обеспечить условие равновесия мостовой схемы. Балансировка мостовой схемы для определенного значения
. В связи с этим удается обеспечить условие равновесия мостовой схемы. Балансировка мостовой схемы для определенного значения  при настройке осуществляется резистором
при настройке осуществляется резистором  или изменением компенсационной индуктивности
или изменением компенсационной индуктивности  .
.
 Мостовые схемы с компенсационной индуктивностью не всегда удобны при практическом исполнении. В этом отношении проще схемы на резистивно-емкостных элементах (см. рис. 4.8.3.1 в). Конденсатор
Мостовые схемы с компенсационной индуктивностью не всегда удобны при практическом исполнении. В этом отношении проще схемы на резистивно-емкостных элементах (см. рис. 4.8.3.1 в). Конденсатор  введен в схему для того, чтобы можно было обеспечить равенство сумм фазовых углов накрест лежащих плеч моста. Регулировкой резистора
введен в схему для того, чтобы можно было обеспечить равенство сумм фазовых углов накрест лежащих плеч моста. Регулировкой резистора  устанавливается требуемый угол фазового сдвига плеча, составленного резисторами
устанавливается требуемый угол фазового сдвига плеча, составленного резисторами  ,
, 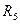 , частично
, частично 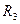 и конденсатором
и конденсатором  и накрест лежащего по отношению к плечу с
и накрест лежащего по отношению к плечу с  . Регулировкой резистора
. Регулировкой резистора 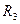 добиваются выполнения условия равенства произведений модулей сопротивлений накрест лежащих плеч. Таким образом оба регулировочных элемента
добиваются выполнения условия равенства произведений модулей сопротивлений накрест лежащих плеч. Таким образом оба регулировочных элемента 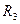 и
и 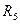 одновременно используются для балансировки мостовой схемы.
одновременно используются для балансировки мостовой схемы.
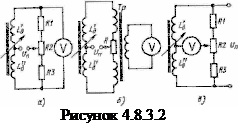
Мостовая схема используется и для включения дифференциальных датчиков. В схеме на рисунке 4.8.3.2 а) два плеча моста образованы индуктивностями обмоток дифференциального датчика, а два других резисторами  ,
,  и
и 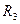 . Поскольку катушки датчика имеют одинаковую конструкцию и одинаковые параметры, то для них углы фазовых сдвигов близки, и второе условие равновесия мостовой схемы обеспечивается автоматически.
. Поскольку катушки датчика имеют одинаковую конструкцию и одинаковые параметры, то для них углы фазовых сдвигов близки, и второе условие равновесия мостовой схемы обеспечивается автоматически.
Для балансировки мостовой схемы при неравных значениях индуктивностей 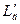 и
и  в процессе настройки служит резистор
в процессе настройки служит резистор  , которым добиваются выполнения первого условия равновесия мостовой схемы.
, которым добиваются выполнения первого условия равновесия мостовой схемы.
 В мостовой схеме, приведенной на рисунке 4.8.3.2 б), плечами моста являются индуктивности датчика
В мостовой схеме, приведенной на рисунке 4.8.3.2 б), плечами моста являются индуктивности датчика 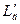 и
и  , а также обмотки трансформатора
, а также обмотки трансформатора 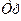 и резистор
и резистор 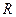 . В этой схеме указатель подключен к измерительной диагонали моста через трансформатор
. В этой схеме указатель подключен к измерительной диагонали моста через трансформатор 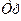 . Такое включение позволяет наилучшим образом согласовать между собой выходное сопротивление мостовой схемы и сопротивление измерителя для получения наибольшей чувствительности.
. Такое включение позволяет наилучшим образом согласовать между собой выходное сопротивление мостовой схемы и сопротивление измерителя для получения наибольшей чувствительности.
Резистор 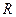 служит для балансировки мостовой схемы при настройке.
служит для балансировки мостовой схемы при настройке.
На рисунке 4.8.3.2 в), в приведена схема, аналогичная показанной на рисунке 4.8.3.2 а), а, но в данном случае изменено назначение диагоналей моста.
Все рассмотренные мостовые схемы работают в режиме неуравновешенного моста, при котором изменение индуктивности датчика размера ведет к пропорциональному изменению выходного напряжения на измерительной диагонали моста.
Выходное напряжение мостовой неуравновешенной схемы
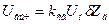 ,
,
где  – относительное изменение полного сопротивления одного плеча (обмотки датчика) мостовой схемы;
– относительное изменение полного сопротивления одного плеча (обмотки датчика) мостовой схемы; 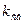 – коэффициент преобразования мостовой схемы (плечевой коэффициент).
– коэффициент преобразования мостовой схемы (плечевой коэффициент).
Величина 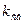 определяется соотношением углов фазовых сдвигов комплексных сопротивлений смежных плеч.
определяется соотношением углов фазовых сдвигов комплексных сопротивлений смежных плеч.
Фазовые соотношения смежных плеч моста:
а – синфазные, б – квадратурные, в – противофазные.

С этой точки зрения мостовые схемы разделяются на
· синфазные, для которых 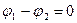 и
и  ;
;
· квадратурные 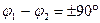 и
и 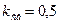 ;
;
· противофазные 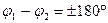 и
и  .
.
Для включения индуктивных датчиков размера на практике применяются только синфазные и квадратурные мостовые схемы, и, следовательно,  .
.
Выражение записано для модуля выходного напряжения без учета фазового сдвига. Из этого выражения нетрудно видеть, что стабильность выходного напряжения  зависит от стабильности напряжения питания
зависит от стабильности напряжения питания  и частоты питания
и частоты питания  (в последнем случае при изменении частоты изменяется
(в последнем случае при изменении частоты изменяется  ). При этом
). При этом
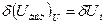 ,
,  .
.
Поскольку в общем виде первое условие равновесия мостовой схемы переменного тока можно записать
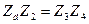 ,
,
то функция преобразования уравновешенной мостовой схемы (при одном уравновешивающем плече  ) будет иметь вид
) будет иметь вид
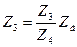 и
и  .
.
При включении в мостовую схему дифференциального индуктивного датчика в выражения и следует подставлять величину  , где
, где  – относительное изменение полного сопротивления обмотки половины дифференциального датчика при входном измеряемом перемещении
– относительное изменение полного сопротивления обмотки половины дифференциального датчика при входном измеряемом перемещении 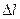 .
.
Похожие статьи:
poznayka.org
5. Делитель напряжения
Между коммутатором и АЦП необходимо установить делитель напряжения, с целью защиты АЦП от отказа и нестабильной работы. На входе АЦП при максимальном значении напряжения на коммутаторе ()необходимо иметь .
Принципиальная схема делителя напряжения:
Рис.№9
На вход подаётся напряжение Uвх= 15 В, то напряжение на выходе будет сниматься с резистора R2 и будет равно Uвых= 2,4 В.
Возьмём общее сопротивление резисторов равным 500 кОм (R1+ R2 =500 кОм), тогда ток протекающий через все сопротивления при входном напряжении будет равен:
(9)
Падение напряжения на резисторе R2 равно U2 = 2,4 В, тогда падение напряжения на резисторе R1 равно U1 = 15-2,4 = 12,6 В
Исходя из падений напряжений на каждом резисторе, найдём номиналы этих резисторов:
(10)
Выберем номинал резистора R1 из ряда Е192, параметры которого:
номинал: 422 кОм;
точность: ±0,25%.
(11)
Выберем номинал резистора R2 из ряда Е192, параметры которого:
номинал: 80,6 кОм;
точность: ±0,25%.
6. Микропроцессорная система
В качестве микропроцессора поставим микросхему STM32F100RB. Микросхема имеет встроенный АЦП. Микропроцессор управляет коммутатором. Сигналы с микропроцессора в дальнейшем подются на индикаторное устройство, на котором сигналы представлены в виде, удобном для восприятия оператором.
Назначение выводов:
1 - вход/выход тестирования
2, 3 - для подключения кварца, LC-цепи
4 - вход установки
5 - вход пошагового выполнения команд
6 - вход сигнала прерывания
7 - вход сигнала разрешения работы с внешней памятью
8 - выход сигнала чтения
9 - выход сигнала управления считыванием из внешней памяти
10 - выход сигнала записи
11 - выход сигнала разрешения фиксации адреса
12...19 – входы/выходы порта 0
21...24, 35...38 - входы/выходы порта 2
20 - общий
25 - выход программирования
26 - напряжение питания при программировании
27...34 - входы/выходы порта 1
39 - вход тестирования
40 - напряжение питания.
Электрические параметры:
Напряжение питания...........4,75…5,25 В
Входное напряжение высокого уровня...
Входное напряжение низкого уровня -0,5…+0,8 В
Выходное напряжение высокого уровня
при =-0,4 мA
Выходное напряжение низкого уровня при = 2 мА
Ток потребления
Выходной ток в состоянии “выключено”
Ток утечки на входах..................
Потребляемая мощность..............580 мВт
Тактовая частота
Емкость нагрузки
Минимальное время выполнения короткой команды 1,36мкс
Условное обозначение микропроцессора. (Рис.№10)
7. Расчет погрешностей
Каждый элемент системы вносит определенную погрешность во всю систему.
1) Погрешность датчика:
Погрешность датчика состоит в нелинейности его характеристики. Расхождение идеальной и реальной характеристик от нелинейного закона составляет 0,1 %. Данная погрешность полностью устраняется при помощи загрузки в микропроцессор специальных команд.
2) Погрешность АЦП обусловлена его конечной чувствительностью, которую можно рассчитать по формуле:
,
где - напряжение с датчика,
- разряд АЦП.
Суммарная погрешность будет чуть больше погрешности АЦП, из за погрешности делителя, но в целом не будет превосходить 0,25% - условия технического задания.
studfiles.net
Делитель напряжения
Делитель напряжения – это устройство, применяемое в схемотехнике для получения меньшего напряжения из большего.
Простейший делитель напряжения представляет из себя два последовательно включенных регулируемых резистора, такой делитель называется резистивным. Участки цепи, в которых заключены резисторы, называются плечами.

Так как резисторы соединены последовательно, то ток через них протекает один и тот же, а значит, с помощью закона Ома, падение напряжения на каждом резисторе можно выразить как:

Если разделить первое выражение на второе, то получим:

Входное напряжение равно сумме падений напряжений на первом и втором резисторах

А так как выходное напряжение равно

можем найти, как соотносятся входное и выходное напряжение

Для обеспечения высокой точности регулировки важно учитывать сопротивление нагрузки, подключаемое параллельно R2, оно должно быть на несколько порядков больше чем R2 (в 10-100 раз).
Для закрепления материала рассмотрим небольшой пример
Каким должно быть сопротивление нижнего плеча, чтобы обеспечить питание лампочки 3 В, от источника ЭДС в 12 В? Сопротивление верхнего плеча – 150 Ом.
Решение :
Выразим из выражения делителя напряжения, сопротивление R2

Сопротивление R2 получилось 50 Ом, проверим, так ли это:

Читайте также - делитель тока
electroandi.ru
Делитель напряжения - это... Что такое Делитель напряжения?
Дели́тель напряже́ния — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи .[1]
В качестве делителя напряжения обычно применяют регулируемые сопротивления (потенциометры). Можно представить как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним, а другое — верхним. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.[1] Сопротивление может быть как активным, так и реактивным.
Резистивный делитель напряжения
Схема простейшего резистивного делителя напряженияПростейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
.
Для каждого резистора:Разделив выражение для на выражение для в итоге получаем: Таким образом, отношение напряжений и в точности равно отношению сопротивлений и .Используя равенство, в котором , а И, выражая из него соотношение для тока:Получим формулу, связывающую выходное ( ) и входное ( ) напряжение делителя:
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.[1]
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если , а — отрицательно, например как на участке вольт-амперной характеристики туннельного диода[источник не указан 213 дней]
Ограничения в применении резистивных делителей напряжения
- Номинал сопротивлений делителя должен быть в 100 - 1000 раз меньше, чем номинальное сопротивление нагрузки.
- Малые значения сопротивлений, являющихся делителем напряжения, приводят к возникновению больших токов в делителе. Снижается КПД схемы из-за нагрева сопротивлений.
- Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
Примечания
- ↑ 1 2 3 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5
Ссылки
dic.academic.ru
7. Делители напряжения | Техническая библиотека lib.qrz.ru
ЭКСПЕРИМЕНТ 7 Делители напряжения
Цели
После проведения данного эксперимента Вы сможете рассчитать выходное напряжение делителя напряжения с нагрузкой и без таковой, а также продемонстрировать, что потенциометр является варьируемым делителем напряжения.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Один потенциометр 10 кОм
* Резисторы — 1/4 Вт, 5%:
один резистор 220 Ом, один резистор 470 Ом, один резистор 1 к0м, один резистор 2, 2 к0м, один резистор 3, 3 к0м, один резистор 10 к0м, один резистор 100 к0м.
ВВОДНАЯ ЧАСТЬ
Делитель напряжения — это резистивная схема, выходное напряжение которой меньше, чем входное напряжение. В электронных схемах часто оказывается необходимым уменьшить уровень напряжения сигнала. Наиболее легко это можно
осуществить при помощи двухрезисторной схемы, известной как делитель напряжения. Входное напряжение прикладывается параллельно к двум резисторам, а выходное напряжение снимается с одного из этих резисторов. Сопротивления этих резисторов выбираются таким образом, чтобы выходное напряжение составляло некоторую определенную часть от входного напряжения.
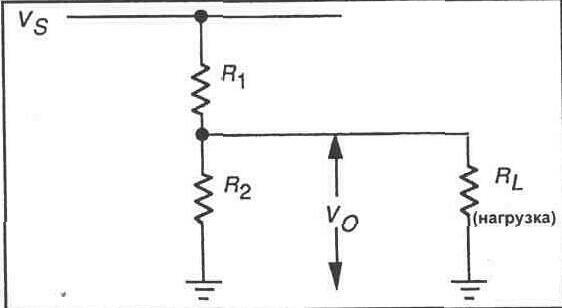
Рис. 7-1.
Широко используемый делитель напряжения показан на рисунке 7-1. Вы можете использовать закон Ома для расчета выходного напряжения, если известны входное напряжение и сопротивления резисторов. Тем не менее, следующая формула ускоряет и упрощает процесс вычислений.
Vo = VsR2/(R1 + R2)
Вычисление выходного напряжения в соответствии с приведенной выше формулой предполагает, что в схеме нет нагрузки. Если параллельно
резистору R2 подключена резистивная нагрузка с конечным сопротивлением, выходное напряжение будет меньше, чем вычисленное, по формуле. Если сопротивление нагрузки приближается к сопротивлению R2, нагрузка будет отбирать все больше и больше тока из схемы. Это приведет к перераспределению падений напряжения в схеме, и выходное напряжение будет уже значительно отличаться от рассчитанного в соответствии с приведенной выше формулой напряжения.
Для определения выходного напряжения делителя при наличии нагрузки Вы можете использовать стандартные методы расчетов в соответствии с законами Ома и Кирхгофа, которые уже применялись Вами в предыдущем эксперименте, чтобы дать заключение о выходном напряжении. Во многих приложениях, тем не менее, это не является необходимым. Если сопротивление нагрузки достаточно велико в сравнении со значением R2, выходное напряжение будет почти равным напряжению, значение которого получается в соответствии с приведенной выше формулой. При этом эмпирическим правилом является: сопротивление нагрузки должно в десять или более раз превышать сопротивление R2. Чем выше значение сопротивления нагрузки по отношению к R2, тем ближе выходное напряжение будет к значению, рассчитанному в соответствии с приведенной ранее формулой.
Потенциометр
Одним из наиболее часто используемых электроэлементов является потенциометр, который фактически представляет собой варьируемый делитель напряжения. Потенциометр — это переменный резистор с тремя выводами (см. рис. 7-2). Центральный вывод соединен с подвижным контактом, который может соединяться с любой точкой резистивного элемента, позволяя гасить часть полного приложенного напряжения. Подвижный контакт может перемещаться от одного конца резистивного элемента к другому, позволяя выбирать любое значение напряжения между напряжением входного источника и нулем. Потенциометры широко используются в электронных схемах, поскольку с их помощью удается точно выполнить настройку выходного напряжения, желательного для конкретного применения.
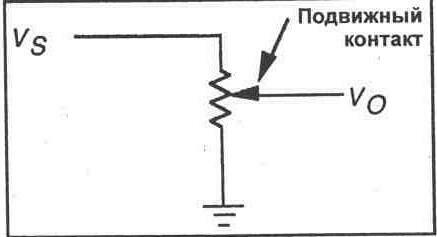
Рис. 7-2.
Краткое содержание
В данном эксперименте Вы соберете и продемонстрируете резистивные делители напряжения, а также покажете изменение выходного напряжения при различных уровнях нагрузки. Вы также
продемонстрируете использование потенциометра в качестве варьируемого делителя напряжения.
ПРОЦЕДУРА
1. Обратитесь к схеме делителя напряжения, показанной на рисунке 7-3. Выполните расчет выходного напряжения с нагрузкой 1 кОм и без нее.
Vo=___В (нагрузка 1 кОм)
Vo = ________ В (без нагрузки)
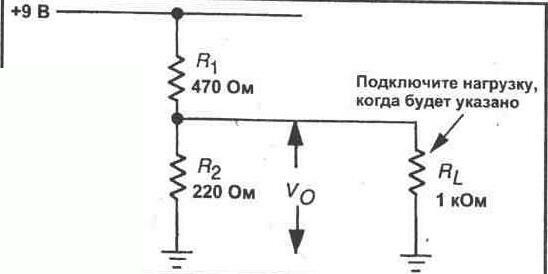
Рис. 7-3.
2. Соберите схему, показанную на рисунке 7-3. Не присоединяйте резистор 1 кОм. Измерьте выходное напряжение на R2. Это напряжение без нагрузки.
Vo=_______В
3. Присоедините нагрузочный резистор 1 кОм параллельно R2, как показано на рисунке 7-3. Измерьте выходное напряжение с подключенной нагрузкой. После этого отсоедините нагрузку
1 кОм и замените ее резистором 10 кОм. Снова измерьте выходное напряжение. Наконец, замените резистор 10 кОм на резистор 100 кОм. Измерьте выходное напряжение. Запишите значения выходных напряжений в таблицу.

4. Основываясь на данных, накопленных в шаге З, укажите, как варьируется выходное напряжение в зависимости от различных сопротивлений нагрузки.
5. Размонтируйте схему на рисунке 7-3. Смонтируйте потенциометр 10 кОм на Вашей макетной панели. Каждый из контактов должен входить в отверстие на отдельном вертикальном ряду отверстий макетной панели. Центральный контакт — это подвижный контакт. Затем подключите к потенциометру источник питания 9 В, как показано на рисунке 7-4. Вы будете измерять выходное напряжение между отрицательным выводом источника и подвижным контактом потенциометра.
6. Подключите Ваш мультиметр на выход потенциометра для измерения выходного напряжения (Vo). При помощи небольшой отвертки полностью выведите подвижный контакт потенциометра против часовой стрелки. Запишите
полученное выходное напряжение. Затем полностью выведите подвижный контакт потенциометра по часовой стрелке. Снова запишите полученное выходное напряжение.
Vo=___В (против часовой стрелки)
Vo=__В (по часовой стрелке)
7. Теперь контролируйте выходное напряжение потенциометра. Отрегулируйте Ваш потенциометр таким образом, чтобы выходное напряжение составляло половину входного напряжения (напряжения источника питания).
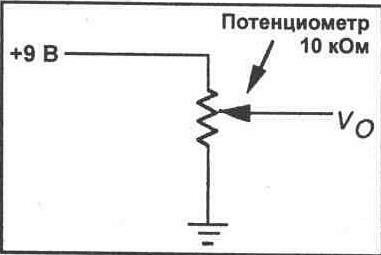
Рис. 7-4.
8. Размонтируйте схему рисунка 7-4.
9. Используя Ваш мультиметр, измерьте сопротивление между центральным выводом (подвижный контакт) и каждым из других выводов потенциометра. Запишите полученные значения. Сопротивление между центральным контактом и одним выводом = ______ Ом
Сопротивление между центральным контактом и другим выводом = ______ Ом
Объясните полученные Вами значения.
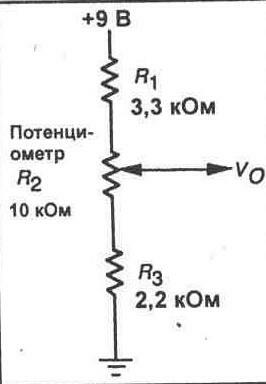
Рис. 7-5.
10. Соберите делитель напряжения, показанный на рисунке 7-5. Рассчитайте, в каком диапазоне может варьироваться выходное напряжение при использовании потенциометра.
Vo = __ В (против часовой стрелки)
Vo = _____ В (по часовой стрелке)
11.Подключите схему к источнику питания. Измеряйте теперь выходное напряжение схемы, варьируя положение подвижного контакта потенциометра по всему его диапазону. Запишите предельные значения напряжения.
Vo = __ В (против часовой стрелки) Vo = _____ В (по часовой стрелке)
ОБЗОРНЫЕ ВОПРОСЫ
1. Делитель напряжения, аналогичный показанному на рисунке 7-1, имеет следующие сопротивления резисторов: R1 = 10 кОм и R2 = 1 кОм.
Источник питания дает напряжение 15В. Выходное напряжение составляет:
а) 1, 28 В,
б) 1, 36 В,
в) 1, 5 В,
г) 1, 72 В.
2. Каково минимальное значение сопротивления нагрузки, которая может подключаться к делителю напряжения из вопроса 1, чтобы выходное напряжение не снижалось значительно?
а) 100 Ом,
б) 1 кОм,
в) 10 кОм,
г) 100 кОм.
3. Варьируемый делитель напряжения — это:
а) потенциометр,
б) переменный резистор,
в) реостат,
г) варистор.
4. Постоянное напряжение 6 В приложено к потенциометру. Выходное напряжение может быть установлено на любое значение в диапазоне:
а) от —6 до+ 6 В,
б) от 0 до 6 В,
в) от 0 до 9 В,
г) от 0 до 12 В.
5. Потенциометр из вопроса 4 настроен так, чтобы гасить 85% приложенного напряжения. При этом выходное напряжение составляет:
а) 0, 9 В,
б) 2, 6 В,
в) 4, 3 В,
г) 5, 1 В.
lib.qrz.ru








Поделиться с друзьями: