Как уже отмечалось выше, последовательной называется схема с памятью. ЭВМ и микропроцессоры частности, являют собой классические примеры систем, поведение которых зависит от событий в прошлом. Состоянием последовательной схемы называется то, что отражает итоговое воздействие прошлых входных воздействий на поведение схемы в данный момент. Для создания последовательных схем необходимо располагать средствам, позволяющими сохранять информацию о состоянии схемы так, чтобы эта информация участвовала при формировании настоящих и будущих входных значений. Простейший элемент, используемый для этой цели - ТРИГГЕР. Триггером называют устройство, обладающее двумя состояниями устойчивого равновесия и способное скачком переходить из одного состояния в другое, под воздействием внешнего управляющего сигнала. Такое устройство можно получить, введя обратную связь. Так как сигналы, вырабатываемые цифровыми схемами, однотипны с сигналами управления этими схемами, то цепи обратной связи в цифровой электронике предельно просты. Они представляют собой соединения выходов с входами. На рис.1.6.1 приведена схема, способная хранить 0 или 1. Рисунок 1.6.1 При подаче на вход X1 такого устройства логический единицы на выходе элемента D1 появляется в обязательном порядке логический 0, который поступает на вход D2; если при этом с входа Х2 приходит логический 0, то на выходе появляется; логическая 1, которая поступает1 на X1, что не меняет состояния всего устройства. При поступлений на X1 логического 0, а на Х2 - 1. на выходе D2 устанавливается 0, который поступает на вход D1, что опять не ведет к изменению состояния всего устройства. При подаче на входы X1 и Х2 логических 0, работа устройства будет определять состояние выхода Q. Если на выходе Q был до этого логический 0, то он поступит на вход D1 и на выходе D1 установится состояние логической 1, которая, поступив на вход D2, сохранит состояние логического 0 на выходе S. При нахождения выходе Q перед подачей сигналов в состоянии логической 1, она поступит ил вход D1 и приведет к появлению логического нуля на выходе D1; два логических нуля на входе D2 будут поддерживать состояние логической 1 на выходе Q. Таким образом, подача сигнала X1 = 0, Х2 = 0 удерживает триггер в прежнем состоянии. По этой причине о входной комбинации Х1 = 0, Х2 = 0 говорят как о случае отсутствия входных сигналов. Наконец, при поступлении на оба входа логической 1 схема окажется в неопределенном состоянии, и поэтому такая комбинация входных сигналов запрещена. Такую схему называют собственно триггером, она является обязательной составной частью любых более сложных триггеров. Нетрудно заметить, что выходы логических элементов D1 и D2 находятся всегда в противоположных состояниях, т.е., если D2 имеет выходной сигнал Q , то D1 будет иметь . Добавим этот инверсный выход и обозначим входы X1 – S (от английского слова set –“установить”), Х2 - R ( от reset – “переустановить”). При подаче на вход S логической 1 (R = 0), триггер устанавливается в состоянии логический 1, а при подаче на R = 1 (S = 0) триггер изменяет свое состояние на противоположное. Поэтому вход R называют ВХОДОМ СБРОСА, a вход S – ВХОДОМ УСТАНОВКИ. Такой триггер называют АСИНХРОННЫМ RS - ТРИГГЕРОМ, его таблица истинности приведена в табл. 1.8.1, а условное обозначение на рис. 1.6.2. Табл. 1.6.1. S R Q 0 0 не измен. 1 0 1 0 0 1 0 1 1 1 не допус. Рис. 1.6.2. Реализовать такой триггер можно и на элементах И-НЕ, но таблица истинности такого триггера будет другой. На рис. 1.6.3 приведены временные диаграммы RS-триггеpa. Пусть в интервале времени 0 - t1, на входах триггера будут логические 0, а на выходе Q - также 0. При появлении в момент времени t1, на входе S = 1, на выходе Q = 1 , т. е. триггер переключится в единичное состояние. Если в момент времени t2 на входе S вновь установится 0, состояние триггера сохранится. При появлении в момент t3 на входе R = 1 триггер переключится в нулевое состояние. Если в момент t4 на входе R снова будет 0, триггер не изменит свое состояние, он будет "помнить" записанную в него информацию. В момент t5 под действием логической 1 на входе S триггер вновь переключится в единичное состояние. Изменение состояния входа S в интервале времени t5 - t9 не изменит состояния триггера и только в момент t9, когда на вход R поступит логическая 1, он вновь переключится в нулевое состояние. Рис. 1.6.3 Различают два типа входов триггеров - информационный и синхронизирующий. Сигналы на информационных входах и исходное состояние выхода S определяют, каким будет новое состояние триггера. Сигналы на синхронизирующих входах определяют время переключения. В таком триггере запись информации производится только по разрешению синхронизирующего импульса и лишь во время его действия. Простейший подобным триггером является СИНХРОННЫЙ RS-ТРИГГЕР. Он получается из асинхронного RS - триггера введением по входам логических схем, запрещающих работу триггера при отсутствии сигнала, подаваемого на вход С – синхронизирующий вход (от английского clock – “часы”) Рис. 1.6.4. В перечисленных выше триггерах их состояние при наличии логических 1 по обоим входам не определено, потому что бессмысленно требовать установки и сброса триггера одновременно. Состояние реального триггера при таких входных сигналах зависит от его устройства. Чтобы этого избежать, необходимо гарантировать подачу на входы R и S противоположных состояний сигнала, что легко сделать введением соответствующего логического элемента. Такой триггер имеет только один информационный вход и носит название D - ТРИГГЕР (от английского delay – “задержка”). Его условное обозначение приведено на рисунке 1.6.5, а таблица истинности в табл. 1.6.2. Табл. 1.6.2. D Q 0 0 1 1 1 0 Рис. 1.6.5. Как видно, для триггера типа D соотношение между сигналом на входе и следующим состоянием триггера формируется проще всего. По синхроимпульсу D - триггер устанавливается в состояние, которое было на входе. Обратная связь помогает не только превратить комбинационную схему в триггер, но и расширить возможности самого триггера. Однако попытка ввести обратную связь в рассмотренные синхронизируемые триггеры наталкивается на определенные трудности. Сигнал обратной связи может измениться до окончания импульса синхронизации и привести к повторному, т.е. незапланированному переключению триггера. Чтобы исключить подобного рода нежелательные явления, применяют триггеры с двухступенчатым запоминанием - двухтактные триггеры, их ещё называют MS - триггеры, по первым буквам английских слов master - slave, “хозяин” - “раб”, подчеркивая тем самым, что триггер состоит из двух частей, одна из которых как бы заставляет другую повторить свои действия. Более правильно говорить о ведущем Т1, и ведомом Т2 триггерах. На рис. 1.6.6 представлена структура и обозначение двухтактного RS - триггера, а на рис. 1.6.7 - двухтактного D - триггера. Рис. 1.6.6. Рис. 1.6.7. Рассмотрим работу двухтактного RS - триггера. Информация, поступившая на входы S и R триггера Т1, записывается в него с приходом тактового импульса. Во время действия тактового импульса на входе С синхронизации триггера Т2 появляется логический 0, закрывающий его входы S и R. По окончании тактового импульса сначала закрываются R и S триггера Т1, а затем информация с его выходов Q и переписывается в триггер Т2, так как на его входе С появляется разрешающий сигнал 1. В таком устройстве памяти повышается помехоустойчивость, т.к. запись информации производится не во время действия тактового импульса, когда входы триггера открыты для помех, а сразу после его окончания, когда они закрыты. Временные диаграммы двухтактного RS-триггера показаны на рис. 1.6.8. Рис. 1.6.8. Пусть в момент времени t1 на входе S появилась логическая 1, а на входах С и R логические 0. В момент t2, с приходом тактового импульса, триггер Т1 переключается в единичное состояние, а T2 остается в нулевом, так как на его входе С - логический 0. В момент t3 заканчивается тактовый импульс и на входе Т2 появляется логическая 1, a R = 0. Состояние T2 изменится на единичное. В это время Т1 закрыт, помехи не в состоянии повлиять на его выходы и изменить информацию, записанную в триггер Т2. Наиболее универсальным триггером является JK -триггер. Своим названием он обязан английским словам Jamp - Keep (“прыгай” – “держись”). Изучение JK - триггера начнем с анализа некоторых способов включения уже известных нам RS- и D - триггеров с двухступенчатым запоминанием, В этих триггерах, как и во всех остальных, наряду с основным обычно предусматривается и инверсный выход . Он не несет никакой дополнительной информации, но в ряде случаев удобен как источник сигнала, противоположного (инверсного) тому, который наблюдается на основном выходе. В схеме на рис. 1.6.9 инверсный выход D-триггера с двухступенчатым запоминанием соединен с его же информационным входом, и поэтому после С-импульса D-триггер переходит из состояния Q в противоположное состояние . После второго С-импульса триггер возвращается в исходное состояние. Иными словами, на выходе такого триггер, в ответ на два импульса на входе появляется один импульс (рис. 1.6.10). Рис. 1.6.9. Рис. 1.6.10. Такой режим работы триггера называют СЧЕТНЫМ, и вход Т, который при этом образовался, тоже счетным; сам триггер получил название Т-триггер, от английского слова time – “времз”. Обозначение Т-триггера на рис. 1.6.11. Рис.1.6.11. Такой режим работы можно получить и в RS-триггере. Структура JK-триггера (рис. 1.6.12) напоминает двухступенчатый RS-триггер с обратными связям, но он имеет более сложную входную логику, исключающую запрещенное состояние входов RS - триггера, когда S = 1, R = 1. Рис. 1.6.12. Работа этого триггера описывается таблицей истинности (табл. 1.6.1), где Q1 и , Q2 исоответствуют выходам, составляяющих двухтактный RS-триггер, обычных RS-триггеров (Т1 – ведущий, Т2 – ведомый триггера). Табл.1.6.13. До Входы После Q1 = Q2 J K Q1 = Q2 0 1 0 0 0 1 0 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 1 0 0 1 0 1 1 0 1 0 1 1 0 1 Рассмотрим первую часть таблица истинности JK-триггера, когда Q1 = Q2 = 0, = = 1. При поступлении на входы J и K логических 0 состояние триггера сохраняется, так как ни одна из входных схем И на пропускает сигналы на входы S и R триггера Т1. При комбинации входных сигналов J = 0, К = 1 сигналы на входы триггера Т1 также не попадут, так как на входы одной схемы И поступят сигналы J = 0, = 1, а на входы другой К = 1,Q2 = 0. При входных сигналах J = 1, К = 0 на вход S триггера Т1 поступит 1. так как на входах схемы И, связанных с этим входом, J = 1, Q2 = 1. Следовательно, состояния триггеров Т1 и Т2 изменятся на противоположные. При комбинации входных сигналов J = 1, К = 1 триггер также переключится в новое состояние, так как на входе S появится логическая 1. Рассуждая аналогично, доказывается и вторая часть таблицы. Основным достоинством JK-триггера является отсутствие запрещенной комбинации на входе. studfiles.net Логические схемы подразделяются на два класса: комбинаторные и последовательные. Выходной сигнал комбинаторной схемы полностью определяется текущими значениями на ее входах. Примерами таких схем могут служить дешифраторы и мультиплексоры, о которых рассказывалось в разделах 2.9 и 2.10. Выход последовательной схемы зависит не только от текущих значений на ее входах, но и от последовательности предыдущих входных значений. Такие схемы могут находиться в разных состояниях, что зависит от того, какой была последовательность предшествующих входных данных. В разделах 2.7 и 2.8 вам встречались два типа таких схем, а именно сдвиговые регистры и счетчики. Ниже мы приведем еще несколько примеров последовательных схем, рассмотрим их общую структуру и базовые принципы разработки. На рис. 2.33 показана конфигурация счетчика с прямым счетом (суммирующего счетчика), реализованного посредством трех триггеров. Этот счетчик считает в таком порядке: 0,1,2,..., 7,0,.... Для обратного счета, то есть счета в порядке 0,7,6,..., 1,0,..., применяются похожие схемы. При построении этих простых схем используется заложенная в Т-триггере возможность переключения состояний. Сейчас же мы рассмотрим возможность реализации счетчиков на основе D-триггеров. В частности, речь пойдет о структуре счетчика, который способен считать как в прямом, так и в обратном порядке, в зависимости от значения на внешнем управляющем входе. Для того чтобы приводимый пример не оказался слишком большим, мы ограничимся счетом по модулю 4, для которого достаточно двух битов состояния, представляющих четыре возможных значения счетчика. Счетчик будет сконструирован на основе стандартной технологии синтеза последовательных схем. Такая схема считает в прямом направлении, если входной сигнал х равен 0, и в обратном, если входной сигнал равен 1. Текущее значение счетчика будет изменяться на отрицательном фронте тактового сигнала. Предположим, что нас особо интересует состояние счетчика в тот момент, когда мы досчитаем до 2. Поэтому при значении счетчика 2 мы будем выдавать выходной сигнал z = 1, а все остальное время сигнал z будет равен 0. Такой счетчик можно реализовать как последовательную схему. Для того чтобы определить новое значение счетчика, которое будет установлено после очередного тактового импульса, достаточно знать значение x и текущее значение счетчика. Предшествующие его значения для этого не нужны. Если текущее значение равно 2 и x = 0, следующим значением будет 3. И не важно, получено текущее значение путем прямого счета от 1 или путем обратного счета от 3. Прежде чем показать, как реализуется такая схема, давайте опишем ее поведение с помощью диаграммы состояний. У нашего счетчика имеется четыре разных состояния: S0, S1, S2 и S3. Диаграмма состояний — это граф, в котором состояния представлены окружностями (иногда называемыми узлами). Переходы между состояниями представлены стрелками с надписями. Связанная со стрелкой надпись указывает, какое значение переменной x вызывает данный переход, и какое значение счетчика получается в результате. Диаграмма состояний для нашего счетчика с прямым/обратным счетом приведена на рис. 2.45. Например, стрелка, исходящая от состояния Sl (счетчик = 1) при x - 0, указывает на состояние S2. При этом сообщается, что пока схема находится в состоянии Sl и x = 0, выходное значение z должно быть равным 0. Стрелка, ведущая от узла S2 к узлу S3, указывает, что когда x = 0, на следующем такте будет выполнен переход в состояние S3, а выходное значение z будет установлено в 1. Обратите внимание, что диаграмма состояний описывает функциональное поведение счетчика вне какой бы то ни было связи с его конкретной реализацией. Так, рис. 2.45 может соответствовать цифровой схеме, механическому счетному устройству или компьютерной программе. Подобные диаграммы позволяют описывать любую систему с последовательным поведением. В качестве альтернативы диаграмме состояний для представления той же информации можно воспользоваться таблицей состояний. Такая таблица для нашего примера приведена на рис. 2.46. В ней описаны переходы из каждого текущего состояния в следующие состояния, определяемые входным значением x. Выходной сигнал z определяется текущим состоянием схемы и входным значением х. Рис. 2.45. Диаграмма состояния для счетчика с прямым/обратным счетом по модулю 4, сигнализирующего о значении 2 Рис. 2.46. Таблица состояний для счетчика с прямым/обратным счетом Определив функциональное поведение счетчика, можно переходить к его физической реализации. Для того чтобы закодировать все четыре состояния счетчика, достаточно двух битов. Обозначим их как y2 (старший бит) и у1 (младший бит). Состояния считчика, определяемые значениями переменных y2 и у1, мы будем записывать в форме y2y1. У нашего счетчика четыре состояния y2y1: S0 = 00, Sl = 01, S2 = 10 и S3 = 11. Как видите, это просто двоичная запись чисел из диапазона от 0 до 3, применяемая для обеспечения наглядности счета. Переменные y2 и у1 называются переменными состояния последовательной схемы. При указанных значениях этих переменных таблицу состояний для нашего примера можно переписать так, как показано на рис. 2.47. Для обозначения следующих состояний в ней используются переменные Y2 и Y1. Мы могли бы выбрать и другие обозначения состояний y2y1. В частности, они могут быть такими: S0 = 10, S1 = 11, S2 = 01 и S3 = 00, Но такие обозначения не совсем логичны, хотя схема прекрасно бы функционировала. Реализация различных состояний обычно требует разных затрат. Мы планировали создать нашу схему на основе D-триггеров, в которых значения двух переменных состояния будут сохраняться между последовательными тактовыми импульсами. Выход Q каждого триггера будет представлять переменную текущего состояния уi, а вход D — переменную следующего состояния Yi. Заметьте, что Yi, является функцией переменных y2y1 и х (это хорошо видно на рис. 2.47). Рис. 2.47. Значения состояний для примера, приведенного на рис. 2.46 На основе представленной здесь таблицы для функций Y2 и Y1 можно составить вот такие выражения; Выходное значение z определяется следующим образом: С учетом этих выражений составляется схема, приведенная на рис. 2.48. Рис. 2.48. Реализация счетчика с прямым/обратным счетом 13Последовательные схемы включения. Последовательные схемы
Глава 1.6 последовательные логические схемы.
2.13. Последовательные схемы
2.13.1. Пример счетчика с прямым/обратным счетом
studfiles.net
Последовательные схемы включения
Варианты последовательных схем показаны на рисунке 4.8.1.1. Индуктивный датчик 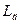 питается переменным напряжением
питается переменным напряжением 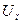 . Величина тока в датчике при постоянной величине питающего напряжения будет зависеть от его сопротивления:
. Величина тока в датчике при постоянной величине питающего напряжения будет зависеть от его сопротивления:  , где
, где 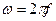 – круговая частота питания схемы,
– круговая частота питания схемы,  – добротность датчика,
– добротность датчика, 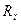 – сопротивление потерь датчика,
– сопротивление потерь датчика,  – частота питающего датчик тока.
– частота питающего датчик тока.
Чувствительность преобразования последовательной схемы
 .
.
Изменение тока (выходной сигнал) при изменении полного сопротивления датчика
 ,
,
где 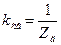 – коэффициент преобразования схемы включения.
– коэффициент преобразования схемы включения.
Схема чувствительна к изменению напряжения питания 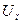 и частоты питающего тока Используя простую последовательную схему включения индуктивного датчика, нельзя получить высокую чувствительность и точность измерений.
и частоты питающего тока Используя простую последовательную схему включения индуктивного датчика, нельзя получить высокую чувствительность и точность измерений.
Последовательная схема может быть безрезонансной и резонансной (см. 4.8.1.1 в). В резонансной схеме ток в цепи будет определяться сопротивлением резонансного контура, состоящего из индуктивности датчика 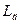 и конденсатора
и конденсатора  . При изменении
. При изменении 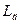 это сопротивление меняется, вызывая изменение тока.
это сопротивление меняется, вызывая изменение тока.
Если частота питающего напряжения  совпадает с собственной частотой колебательного контура
совпадает с собственной частотой колебательного контура 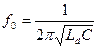 , то сопротивление последовательного колебательного контура минимально, а параллельного – максимально. При изменении индуктивности датчика
, то сопротивление последовательного колебательного контура минимально, а параллельного – максимально. При изменении индуктивности датчика 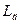 равенство частот будет нарушено, и сопротивление
равенство частот будет нарушено, и сопротивление
последовательного контура будет увеличиваться, а параллельного – уменьшаться. Соответствующим образом будет изменяться и ток в цепи. Чувствительность резонансной последовательной схемы в несколько раз выше чувствительности безрезонансной последовательной схемы.
 Вариант последовательной схемы для включения дифференциального датчика показан на рисунке 4.8.1.2. Каждая половина датчика
Вариант последовательной схемы для включения дифференциального датчика показан на рисунке 4.8.1.2. Каждая половина датчика 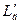 и
и  питается переменным током с напряжением
питается переменным током с напряжением 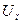 . При изменении измеряемого размера одна индуктивность уменьшается, а другая увеличивается на одну и ту же величину. Соответствующим образом изменяются токи в цепях обмоток датчиков. Эти токи
. При изменении измеряемого размера одна индуктивность уменьшается, а другая увеличивается на одну и ту же величину. Соответствующим образом изменяются токи в цепях обмоток датчиков. Эти токи 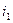 и
и  выпрямляются диодами
выпрямляются диодами  и
и  и во встречной полярности протекают через измеритель тока А. Измеритель тока будет показывать разницу токов в цепях обмоток
и во встречной полярности протекают через измеритель тока А. Измеритель тока будет показывать разницу токов в цепях обмоток 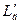 и
и 
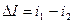 . При равенстве полных сопротивлений
. При равенстве полных сопротивлений 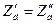 токи в их цепях будут равны, и амперметр А покажет нуль. При изменении измеряемого размера равенство сопротивлений нарушится, и показания амперметра будут отличаться от нуля.
токи в их цепях будут равны, и амперметр А покажет нуль. При изменении измеряемого размера равенство сопротивлений нарушится, и показания амперметра будут отличаться от нуля.
Направление тока через амперметр будет зависеть от того, в цепи какой катушки 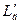 или
или  ток в данный момент больше.
ток в данный момент больше.
Такие схемы включения дифференциальных индуктивных датчиков, которые реагируют не только на величину смещения измерительного стержня из нулевого положения, но и на направление смещения, называют фазочувствительными.
Схемы делителей напряжения
При включении по схеме делителя напряжения датчик включается в цепь последовательно с некоторым постоянным сопротивлением  , которое в общем виде может быть комплексным. Добавочным сопротивлением может служить, например, резистор, индуктивность или емкость (см. рис. 4.8.2.1). При питании цепи переменным напряжением, напряжение на датчике, измеряемое вольтметром V того или иного типа, будет зависеть от полного сопротивления датчика. Если соблюдается условие
, которое в общем виде может быть комплексным. Добавочным сопротивлением может служить, например, резистор, индуктивность или емкость (см. рис. 4.8.2.1). При питании цепи переменным напряжением, напряжение на датчике, измеряемое вольтметром V того или иного типа, будет зависеть от полного сопротивления датчика. Если соблюдается условие  , то
, то
 ,
,
откуда следует, что напряжение на датчике прямо пропорционально величине его индуктивности.
Чувствительность по напряжению схемы
 .
.
Выходной сигнал схемы включения при изменении полного сопротивления датчика
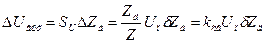 .
.
С другой стороны, выходное напряжение схемы делителя напряжения зависит также от величины напряжения питания 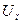 и частоты питающего тока
и частоты питающего тока  . Нетрудно убедиться, что
. Нетрудно убедиться, что  и
и 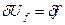 ; следовательно, стабильность источника питания по частоте и напряжению определяет погрешность преобразования измерительного сигнала схемой делителя напряжения.
; следовательно, стабильность источника питания по частоте и напряжению определяет погрешность преобразования измерительного сигнала схемой делителя напряжения.

Включение дифференциального датчика в схему делителя напряжения показано на рисунке 4.8.2.2. Обмотки датчика 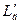 и
и  образуют делитель напряжения, питаемый переменным током.
образуют делитель напряжения, питаемый переменным током.
При изменении индуктивностей обмоток будет изменяться их полное сопротивление и падение напряжения на обмотках. Это падение напряжения выпрямляется диодами 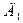 и
и  . Конденсаторы
. Конденсаторы  и
и 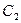 служат для сглаживания пульсаций выпрямленного напряжения, а резисторы
служат для сглаживания пульсаций выпрямленного напряжения, а резисторы  ,
,  ,
,  являются сопротивлениями нагрузки для выпрямителей.
являются сопротивлениями нагрузки для выпрямителей.
Показывающий вольтметр V подключен к одноименным полюсам выпрямителей. В этом случае он будет показывать разницу напряжений на обмотках датчика 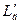 и
и  . Когда индуктивности обмоток равны, равны и их полные сопротивления и падения напряжения на них. Вольтметр при этом покажет нуль. Регулировка нулевых показаний вольтметра при настройке может осуществляться переменным резистором
. Когда индуктивности обмоток равны, равны и их полные сопротивления и падения напряжения на них. Вольтметр при этом покажет нуль. Регулировка нулевых показаний вольтметра при настройке может осуществляться переменным резистором  .
.
Мостовые схемы
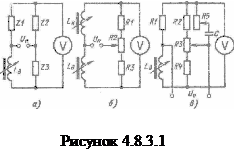
Весьма широкое распространение для включения индуктивных датчиков нашла мостовая схема включения в различных вариантах (см. рис. 4.8.3.1). Общий вид мостовых схем включения недифференциального индуктивного датчика показан на рисунке. Если соблюдается условие
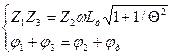
 где
где  – фазовый угол соответствующего комплексного сопротивления, то выходное напряжение
– фазовый угол соответствующего комплексного сопротивления, то выходное напряжение  равно нулю, и мост в этом случае сбалансирован или уравновешен. Условие равновесия мостовой схемы формулируется следующим образом: «для равновесия мостовой схемы необходимо, чтобы произведения модулей комплексных сопротивлений накрест лежащих плеч моста, а также суммы их углов фазовых сдвигов были равны между собой». При изменении индуктивности датчика условие равновесия моста нарушается, и выходное напряжение моста пропорционально изменению индуктивности.
равно нулю, и мост в этом случае сбалансирован или уравновешен. Условие равновесия мостовой схемы формулируется следующим образом: «для равновесия мостовой схемы необходимо, чтобы произведения модулей комплексных сопротивлений накрест лежащих плеч моста, а также суммы их углов фазовых сдвигов были равны между собой». При изменении индуктивности датчика условие равновесия моста нарушается, и выходное напряжение моста пропорционально изменению индуктивности.
Плечи мостовой схемы в общем случае являются комплексными сопротивлениями и в конкретных схемах включения могут быть реализованы включением резисторов, индуктивностей или емкостей. Пример реализации мостовой схемы приведен на рисунке 4.8.3.1 б). Одним плечом моста является индуктивность датчика 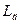 , второе плечо – компенсационная индуктивность
, второе плечо – компенсационная индуктивность  , третье и четвертое – образованы резисторами
, третье и четвертое – образованы резисторами  ,
,  и
и  . Для резисторов фазовый угол
. Для резисторов фазовый угол 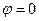 . Для индуктивностей
. Для индуктивностей 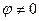 . В связи с этим удается обеспечить условие равновесия мостовой схемы. Балансировка мостовой схемы для определенного значения
. В связи с этим удается обеспечить условие равновесия мостовой схемы. Балансировка мостовой схемы для определенного значения 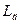 при настройке осуществляется резистором
при настройке осуществляется резистором  или изменением компенсационной индуктивности
или изменением компенсационной индуктивности  .
.
 Мостовые схемы с компенсационной индуктивностью не всегда удобны при практическом исполнении. В этом отношении проще схемы на резистивно-емкостных элементах (см. рис. 4.8.3.1 в). Конденсатор
Мостовые схемы с компенсационной индуктивностью не всегда удобны при практическом исполнении. В этом отношении проще схемы на резистивно-емкостных элементах (см. рис. 4.8.3.1 в). Конденсатор  введен в схему для того, чтобы можно было обеспечить равенство сумм фазовых углов накрест лежащих плеч моста. Регулировкой резистора
введен в схему для того, чтобы можно было обеспечить равенство сумм фазовых углов накрест лежащих плеч моста. Регулировкой резистора 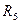 устанавливается требуемый угол фазового сдвига плеча, составленного резисторами
устанавливается требуемый угол фазового сдвига плеча, составленного резисторами  ,
, 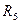 , частично
, частично  и конденсатором
и конденсатором  и накрест лежащего по отношению к плечу с
и накрест лежащего по отношению к плечу с 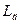 . Регулировкой резистора
. Регулировкой резистора  добиваются выполнения условия равенства произведений модулей сопротивлений накрест лежащих плеч. Таким образом оба регулировочных элемента
добиваются выполнения условия равенства произведений модулей сопротивлений накрест лежащих плеч. Таким образом оба регулировочных элемента  и
и 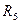 одновременно используются для балансировки мостовой схемы.
одновременно используются для балансировки мостовой схемы.
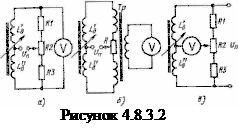
Мостовая схема используется и для включения дифференциальных датчиков. В схеме на рисунке 4.8.3.2 а) два плеча моста образованы индуктивностями обмоток дифференциального датчика, а два других резисторами  ,
,  и
и  . Поскольку катушки датчика имеют одинаковую конструкцию и одинаковые параметры, то для них углы фазовых сдвигов близки, и второе условие равновесия мостовой схемы обеспечивается автоматически.
. Поскольку катушки датчика имеют одинаковую конструкцию и одинаковые параметры, то для них углы фазовых сдвигов близки, и второе условие равновесия мостовой схемы обеспечивается автоматически.
Для балансировки мостовой схемы при неравных значениях индуктивностей 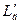 и
и  в процессе настройки служит резистор
в процессе настройки служит резистор  , которым добиваются выполнения первого условия равновесия мостовой схемы.
, которым добиваются выполнения первого условия равновесия мостовой схемы.
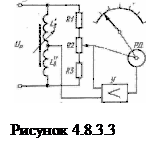 В мостовой схеме, приведенной на рисунке 4.8.3.2 б), плечами моста являются индуктивности датчика
В мостовой схеме, приведенной на рисунке 4.8.3.2 б), плечами моста являются индуктивности датчика 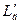 и
и  , а также обмотки трансформатора
, а также обмотки трансформатора  и резистор
и резистор  . В этой схеме указатель подключен к измерительной диагонали моста через трансформатор
. В этой схеме указатель подключен к измерительной диагонали моста через трансформатор  . Такое включение позволяет наилучшим образом согласовать между собой выходное сопротивление мостовой схемы и сопротивление измерителя для получения наибольшей чувствительности.
. Такое включение позволяет наилучшим образом согласовать между собой выходное сопротивление мостовой схемы и сопротивление измерителя для получения наибольшей чувствительности.
Резистор  служит для балансировки мостовой схемы при настройке.
служит для балансировки мостовой схемы при настройке.
На рисунке 4.8.3.2 в), в приведена схема, аналогичная показанной на рисунке 4.8.3.2 а), а, но в данном случае изменено назначение диагоналей моста.
Все рассмотренные мостовые схемы работают в режиме неуравновешенного моста, при котором изменение индуктивности датчика размера ведет к пропорциональному изменению выходного напряжения на измерительной диагонали моста.
Выходное напряжение мостовой неуравновешенной схемы
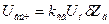 ,
,
где  – относительное изменение полного сопротивления одного плеча (обмотки датчика) мостовой схемы;
– относительное изменение полного сопротивления одного плеча (обмотки датчика) мостовой схемы; 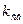 – коэффициент преобразования мостовой схемы (плечевой коэффициент).
– коэффициент преобразования мостовой схемы (плечевой коэффициент).
Величина 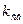 определяется соотношением углов фазовых сдвигов комплексных сопротивлений смежных плеч.
определяется соотношением углов фазовых сдвигов комплексных сопротивлений смежных плеч.
Фазовые соотношения смежных плеч моста:
а – синфазные, б – квадратурные, в – противофазные.

С этой точки зрения мостовые схемы разделяются на
· синфазные, для которых 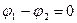 и
и  ;
;
· квадратурные 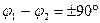 и
и  ;
;
· противофазные 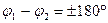 и
и 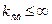 .
.
Для включения индуктивных датчиков размера на практике применяются только синфазные и квадратурные мостовые схемы, и, следовательно, 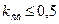 .
.
Выражение записано для модуля выходного напряжения без учета фазового сдвига. Из этого выражения нетрудно видеть, что стабильность выходного напряжения  зависит от стабильности напряжения питания
зависит от стабильности напряжения питания 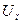 и частоты питания
и частоты питания  (в последнем случае при изменении частоты изменяется
(в последнем случае при изменении частоты изменяется 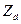 ). При этом
). При этом
 ,
, 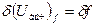 .
.
Поскольку в общем виде первое условие равновесия мостовой схемы переменного тока можно записать
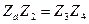 ,
,
то функция преобразования уравновешенной мостовой схемы (при одном уравновешивающем плече 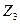 ) будет иметь вид
) будет иметь вид
 и
и 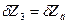 .
.
При включении в мостовую схему дифференциального индуктивного датчика в выражения и следует подставлять величину 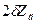 , где
, где  – относительное изменение полного сопротивления обмотки половины дифференциального датчика при входном измеряемом перемещении
– относительное изменение полного сопротивления обмотки половины дифференциального датчика при входном измеряемом перемещении  .
.
Частотная схема включения
 Для преобразования индуктивности датчика в частоту переменного тока применяют генераторные схемы (см. рис. 4.8.4). Основой генераторной схемы является колебательный контур, составленный индуктивностью датчика
Для преобразования индуктивности датчика в частоту переменного тока применяют генераторные схемы (см. рис. 4.8.4). Основой генераторной схемы является колебательный контур, составленный индуктивностью датчика 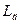 и постоянной емкостью
и постоянной емкостью  .
.
Контур включен в схему электронного генератора Г, который генерирует переменное напряжение с частотой, равной собственной частоте колебательного контура.
При изменении индуктивности датчика изменяется частота на выходе генератора, измеряемая частотомером. Частота генератора зависит в основном от индуктивности датчика и не зависит от его сопротивления потерь (это верно только в первом приближении). Поскольку сопротивление потерь датчика обычно в большой степени зависит от различных внешних факторов, то избавление от его влияния на результаты измерения повышает точность измерений.
Генераторная схема может применяться для включения, как недифференциальных датчиков, так и дифференциальных. В последнем случае имеется два колебательных контура, составленных каждой обмоткой датчика и конденсаторами  и
и 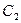 , и два генератора Г1 и Г2. Частоты с обоих генераторов
, и два генератора Г1 и Г2. Частоты с обоих генераторов 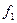 и
и 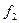 поступают на смеситель, который выделяет разностную частоту. Эта разностная частота, в свою очередь, измеряется частотомером. Подбором емкостей
поступают на смеситель, который выделяет разностную частоту. Эта разностная частота, в свою очередь, измеряется частотомером. Подбором емкостей  и
и 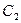 генераторы настраиваются так, чтобы в одном из крайних положений измерительного стержня датчика выполнялось условие
генераторы настраиваются так, чтобы в одном из крайних положений измерительного стержня датчика выполнялось условие 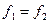 и
и  . Тогда показания частотомера будут пропорциональны величине смещения измерительного стержня из крайнего положения.
. Тогда показания частотомера будут пропорциональны величине смещения измерительного стержня из крайнего положения.
Чувствительность преобразования частотной схемы включения

и относительная чувствительность
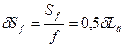 .
.
Сравнение чувствительности преобразования частотной схемы с чувствительностью других описанных схем показывает, что ее относительная чувствительность в 2 раза ниже, как это следует из формулы.
infopedia.su
Последовательные схемы включения

 питается переменным напряжением
питается переменным напряжением  . Величина тока в датчике при постоянной величине питающего напряжения будет зависеть от его сопротивления:
. Величина тока в датчике при постоянной величине питающего напряжения будет зависеть от его сопротивления:  , где
, где 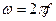 – круговая частота питания схемы,
– круговая частота питания схемы,  – добротность датчика,
– добротность датчика,  – сопротивление потерь датчика,
– сопротивление потерь датчика,  – частота питающего датчик тока.
– частота питающего датчик тока.
Чувствительность преобразования последовательной схемы
 .
.
Изменение тока (выходной сигнал) при изменении полного сопротивления датчика
 ,
,
где 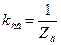 – коэффициент преобразования схемы включения.
– коэффициент преобразования схемы включения.
Схема чувствительна к изменению напряжения питания  и частоты питающего тока Используя простую последовательную схему включения индуктивного датчика, нельзя получить высокую чувствительность и точность измерений.
и частоты питающего тока Используя простую последовательную схему включения индуктивного датчика, нельзя получить высокую чувствительность и точность измерений.
Последовательная схема может быть безрезонансной и резонансной (см. 4.8.1.1 в). В резонансной схеме ток в цепи будет определяться сопротивлением резонансного контура, состоящего из индуктивности датчика  и конденсатора
и конденсатора  . При изменении
. При изменении  это сопротивление меняется, вызывая изменение тока.
это сопротивление меняется, вызывая изменение тока.
Если частота питающего напряжения  совпадает с собственной частотой колебательного контура
совпадает с собственной частотой колебательного контура  , то сопротивление последовательного колебательного контура минимально, а параллельного – максимально. При изменении индуктивности датчика
, то сопротивление последовательного колебательного контура минимально, а параллельного – максимально. При изменении индуктивности датчика  равенство частот будет нарушено, и сопротивление
равенство частот будет нарушено, и сопротивление
последовательного контура будет увеличиваться, а параллельного – уменьшаться. Соответствующим образом будет изменяться и ток в цепи. Чувствительность резонансной последовательной схемы в несколько раз выше чувствительности безрезонансной последовательной схемы.
 Вариант последовательной схемы для включения дифференциального датчика показан на рисунке 4.8.1.2. Каждая половина датчика
Вариант последовательной схемы для включения дифференциального датчика показан на рисунке 4.8.1.2. Каждая половина датчика 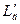 и
и  питается переменным током с напряжением
питается переменным током с напряжением  . При изменении измеряемого размера одна индуктивность уменьшается, а другая увеличивается на одну и ту же величину. Соответствующим образом изменяются токи в цепях обмоток датчиков. Эти токи
. При изменении измеряемого размера одна индуктивность уменьшается, а другая увеличивается на одну и ту же величину. Соответствующим образом изменяются токи в цепях обмоток датчиков. Эти токи 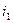 и
и  выпрямляются диодами
выпрямляются диодами  и
и  и во встречной полярности протекают через измеритель тока А. Измеритель тока будет показывать разницу токов в цепях обмоток
и во встречной полярности протекают через измеритель тока А. Измеритель тока будет показывать разницу токов в цепях обмоток 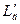 и
и 
 . При равенстве полных сопротивлений
. При равенстве полных сопротивлений  токи в их цепях будут равны, и амперметр А покажет нуль. При изменении измеряемого размера равенство сопротивлений нарушится, и показания амперметра будут отличаться от нуля.
токи в их цепях будут равны, и амперметр А покажет нуль. При изменении измеряемого размера равенство сопротивлений нарушится, и показания амперметра будут отличаться от нуля.
Направление тока через амперметр будет зависеть от того, в цепи какой катушки 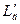 или
или  ток в данный момент больше.
ток в данный момент больше.
Такие схемы включения дифференциальных индуктивных датчиков, которые реагируют не только на величину смещения измерительного стержня из нулевого положения, но и на направление смещения, называют фазочувствительными.
Похожие статьи:
poznayka.org
7.1. Имс двоичных компараторов
На рис. 79,а представлено УГО двоичного компаратора, реализующего по выходу полный набор функций сравнения. В качестве примера на рис. 79 приведены ИМС двоичных компараторов 555СП1 (б) и 74LS683 (в) с триггерами Шмитта на входах.
Рис. 79
В приведенных ИМС осуществляется параллельное сравнение, функции сравнения <, > , = программируются сигналами Е, Н0, F0.
Для реализации многоразрядных схем сравнения отдельные ИМС включаются последовательно (рис. 80).
Рис. 80
На рис. 81 приведена 12-разрядная схема сравнения на ИМС 561ИП2 при последовательном включении. Внешние сигналы H0,F0и Е устанавливают режим сравнения и выбирают выходные функции сравнения.
Рис. 81
7.2. Последовательные схемы сравнения
Последовательные схемы сравнения удобны при представлении двоичных чисел в последовательном коде, а также требуют для реализации значительно меньше логических элементов. На рис. 82 представлена функциональная схема последовательного двоичного компаратора. Поскольку при сравнении получается три результата: G(A>B), H(A=B), F(A<B), то схема содержит два триггера, которые необходимы для хранения промежуточных значений функций сравнения. На выходах триггеров после поразрядного сравнения фиксируются результирующие значения функций. Данная схема не зависит от количества разрядов чисел А и В. Разрядность входных чисел определяет количество циклов сравнения, которое в свою очередь определяет время сравнения.
Рис. 82
13. Умножители двоичных чисел
Операция умножения требует значительных временных затрат, поэтому разработаны различные варианты схем умножения, обеспечивающие максимальное быстродействие. Высокое быстродействие имеют комбинационные схемы умножения. Простейший способ умножения двух n- и m-разрядных чисел описывается следующим алгоритмом:
,
где X – n-разрядное множимое,
Y – m-разрядный множитель,
Pj=X yj2j – частные произведения.
В качестве примера приведен процесс умножения двух чисел с разрядностью n = m = 4.
На рис. 83 приведена схема 4-х разрядного умножителя, реализованного по приведенному алгоритму с использованием ИМС полных сумматоров.
Рис. 83
13.1. Матричные умножители
Алгоритм матричного умножения можно записать в виде: XnґYm+An+Bm, где An и Bm – дополнения из младших разрядов при умножении. Максимальная разрядность результата умножения определяется выражением 2n+m-1 и определяется суммой разрядностей операндов.
Для 2-х разрядных чисел n = m = 2 можно записать алгоритм умножения в виде:
X2×Y2+A2+B2 = x1x0 ґy1y0+a1a0+b1b0 = x1y122 + (x1y0+x0y1+a1+b1)21 + (x0y0+a0+b0)20.
Такое вычисление можно реализовать с помощью четырех одноразрядных сумматоров типа ИМ1 (рис. 84).
Рис. 84
Операция умножения xi yi осуществляется логическими элементами «И», которые являются входными блоками сумматоров ИМ1. Сумма и перенос определяется выражениями:
Графически формирование произведения можно представить в виде:
Такая схема имеет регулярную структуру и может быть расширена до любых значений. Комбинационные схемы, имеющие такую функцию, называются матричными умножителями.
По данной схеме выполнена ИМС ИП5 – матричный умножитель 2ґ2. Условное обозначение MPL (Multiplier - умножитель) (рис. 85,а). Одноразрядные сумматоры в ИМС ИП5 реализованы по схеме на рис. 85,б.
Рис. 85
Существуют быстрые матричные умножители, использующие ускоренный алгоритм вычисления частичных произведений. Например: ИП8, ИК1 – быстрые умножители 4ґ2.
1802ВР4 – специализированная БИС умножения 12ґ12; tумн»100нсек, Pпот= 3Вт. Функциональная схема 1802ВР4 предсталвена на рис. 86.
Сигналы TCY, TCX указывают на дополнительный код умножаемых чисел.
CL и CM – (L – Least - младший, M – Most - старший) – тактовые сигналы записи младшей и старшей групп произведения.
SU – сдвигающее устройство.
Сигнал (Right Shift – сдвиг вправо) указывает на присвоение знака произведения младшей группе.
Рис. 86.
FT – сигнал «прозрачности» регистров произведения.
По аналогичной структуре реализованы матричные умножители типа 1802ВР3 – 8х8 и 1802ВР5 – 16х16.
В настоящее время максимальную производительность обеспечивают умножители, реализованные на ПЗУ.
studfiles.net
2.13. Последовательные схемы
Логические схемы подразделяются на два класса: комбинаторные и последовательные. Выходной сигнал комбинаторной схемы полностью определяется текущими значениями на ее входах. Примерами таких схем могут служить дешифраторы и мультиплексоры, о которых рассказывалось в разделах 2.9 и 2.10. Выход последовательной схемы зависит не только от текущих значений на ее входах, но и от последовательности предыдущих входных значений. Такие схемы могут находиться в разных состояниях, что зависит от того, какой была последовательность предшествующих входных данных. В разделах 2.7 и 2.8 вам встречались два типа таких схем, а именно сдвиговые регистры и счетчики. Ниже мы приведем еще несколько примеров последовательных схем, рассмотрим их общую структуру и базовые принципы разработки.
2.13.1. Пример счетчика с прямым/обратным счетом
На рис. 2.33 показана конфигурация счетчика с прямым счетом (суммирующего счетчика), реализованного посредством трех триггеров. Этот счетчик считает в таком порядке: 0,1,2,..., 7,0,.... Для обратного счета, то есть счета в порядке 0,7,6,..., 1,0,..., применяются похожие схемы. При построении этих простых схем используется заложенная в Т-триггере возможность переключения состояний.
Сейчас же мы рассмотрим возможность реализации счетчиков на основе D-триггеров. В частности, речь пойдет о структуре счетчика, который способен считать как в прямом, так и в обратном порядке, в зависимости от значения на внешнем управляющем входе. Для того чтобы приводимый пример не оказался слишком большим, мы ограничимся счетом по модулю 4, для которого достаточно двух битов состояния, представляющих четыре возможных значения счетчика. Счетчик будет сконструирован на основе стандартной технологии синтеза последовательных схем. Такая схема считает в прямом направлении, если входной сигнал х равен 0, и в обратном, если входной сигнал равен 1. Текущее значение счетчика будет изменяться на отрицательном фронте тактового сигнала. Предположим, что нас особо интересует состояние счетчика в тот момент, когда мы досчитаем до 2. Поэтому при значении счетчика 2 мы будем выдавать выходной сигнал z = 1, а все остальное время сигнал z будет равен 0.
Такой счетчик можно реализовать как последовательную схему. Для того чтобы определить новое значение счетчика, которое будет установлено после очередного тактового импульса, достаточно знать значение x и текущее значение счетчика. Предшествующие его значения для этого не нужны. Если текущее значение равно 2 и x = 0, следующим значением будет 3. И не важно, получено текущее значение путем прямого счета от 1 или путем обратного счета от 3.
Прежде чем показать, как реализуется такая схема, давайте опишем ее поведение с помощью диаграммы состояний. У нашего счетчика имеется четыре разных состояния: S0, S1, S2 и S3. Диаграмма состояний — это граф, в котором состояния представлены окружностями (иногда называемыми узлами). Переходы между состояниями представлены стрелками с надписями. Связанная со стрелкой надпись указывает, какое значение переменной x вызывает данный переход, и какое значение счетчика получается в результате. Диаграмма состояний для нашего счетчика с прямым/обратным счетом приведена на рис. 2.45. Например, стрелка, исходящая от состояния Sl (счетчик = 1) при x - 0, указывает на состояние S2. При этом сообщается, что пока схема находится в состоянии Sl и x = 0, выходное значение z должно быть равным 0. Стрелка, ведущая от узла S2 к узлу S3, указывает, что когда x = 0, на следующем такте будет выполнен переход в состояние S3, а выходное значение z будет установлено в 1.
Обратите внимание, что диаграмма состояний описывает функциональное поведение счетчика вне какой бы то ни было связи с его конкретной реализацией. Так, рис. 2.45 может соответствовать цифровой схеме, механическому счетному устройству или компьютерной программе. Подобные диаграммы позволяют описывать любую систему с последовательным поведением.
В качестве альтернативы диаграмме состояний для представления той же информации можно воспользоваться таблицей состояний. Такая таблица для нашего примера приведена на рис. 2.46. В ней описаны переходы из каждого текущего состояния в следующие состояния, определяемые входным значением x. Выходной сигнал z определяется текущим состоянием схемы и входным значением х.
Рис. 2.45. Диаграмма состояния для счетчика с прямым/обратным счетом по модулю 4, сигнализирующего о значении 2
Рис. 2.46. Таблица состояний для счетчика с прямым/обратным счетом
Определив функциональное поведение счетчика, можно переходить к его физической реализации. Для того чтобы закодировать все четыре состояния счетчика, достаточно двух битов. Обозначим их как y2 (старший бит) и у1 (младший бит). Состояния считчика, определяемые значениями переменных y2 и у1, мы будем записывать в форме y2y1. У нашего счетчика четыре состояния y2y1: S0 = 00, Sl = 01, S2 = 10 и S3 = 11. Как видите, это просто двоичная запись чисел из диапазона от 0 до 3, применяемая для обеспечения наглядности счета. Переменные y2 и у1 называются переменными состояния последовательной схемы. При указанных значениях этих переменных таблицу состояний для нашего примера можно переписать так, как показано на рис. 2.47. Для обозначения следующих состояний в ней используются переменные Y2 и Y1.
Мы могли бы выбрать и другие обозначения состояний y2y1. В частности, они могут быть такими: S0 = 10, S1 = 11, S2 = 01 и S3 = 00, Но такие обозначения не совсем логичны, хотя схема прекрасно бы функционировала. Реализация различных состояний обычно требует разных затрат.
Мы планировали создать нашу схему на основе D-триггеров, в которых значения двух переменных состояния будут сохраняться между последовательными тактовыми импульсами. Выход Q каждого триггера будет представлять переменную текущего состояния уi, а вход D — переменную следующего состояния Yi. Заметьте, что Yi, является функцией переменных y2y1 и х (это хорошо видно на рис. 2.47).
Рис. 2.47. Значения состояний для примера, приведенного на рис. 2.46
На основе представленной здесь таблицы для функций Y2 и Y1 можно составить вот такие выражения;
Выходное значение z определяется следующим образом:
С учетом этих выражений составляется схема, приведенная на рис. 2.48.
Рис. 2.48. Реализация счетчика с прямым/обратным счетом
13
studfiles.net
4. Последовательные схемы
Цели
После проведения данного эксперимента Вы сможете рассчитывать общее сопротивление нескольких включенных последовательно резисторов и использовать закон Кирхгофа для напряжений, чтобы осуществлять расчеты и измерения для последовательных схем.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения * Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом,
один резистор 680 Ом,
один резистор 2, 2 кОм,
один резистор 4, 7 кОм,
один светоизлучающий диод (LED).
ВВОДНАЯ ЧАСТЬ
Имеется два основных способа подключения электронных компонентов к источнику питания. При последовательном включении все компоненты подключаются концами друг к другу, образуя простую цепочку, которая соединяется с источником питания. При параллельном включении (эксперимент 5) каждый из отдельных компонентов подключается непосредственно к источнику питания. Естественно, имеются более сложные схемы, в которых используются те или иные комбинации последовательных и параллельных соединений (эксперимент 6). В данном эксперименте Вы узнаете, как выполнять последовательное включение компонентов и осуществлять различные расчеты и измерения.
Сначала познакомимся с тем, как вычислять общее сопротивление последовательной схемы. Если два или более резисторов включены последовательно, общее сопротивление комбинации равно простой сумме отдельных сопротивлений.
Типичная последовательная схема показана на рисунке 4-1. Общее сопротивление Rт равно сумме отдельных сопротивлений, то есть:
Rт=R1+ R2+ R3
При показанных значениях сопротивлений резисторов общее сопротивление равно:
Rт= 50+ 75+ 30 = 1550м
Три отдельных резистора могут быть заменены единственным резистором с номиналом 155 Ом, при этом никаких изменений в токе схемы не будет.
Падение напряжения
Когда ток протекает через последовательную схему, на каждом сопротивлении происходит падение напряжения. Па рисунке 4-1 показана последовательная схема с напряжениями, указанными для каждого сопротивления. Заметьте полярность падения напряжения на каждом резисторе.
Рис. 4-1.
Конечно, напряжение, падающее на каждом резисторе, может определяться на основании закона Ома. В данном случае общин ток схемы умножается на величину сопротивления каждого резистора для получения соответствующего падения напряжения. Например, напряжение на R2:
V2 = IR2
Исключительно важной характеристикой последовательной схемы, что надо хорошо запомнить,
является то, что сумма отдельных падений напряжения равна напряжению источника. Заметьте на рисунке 4-1, что сумма, полученная сложением напряжений на резисторах R1, R2, и R3 такая же, как и общее приложенное напряжение.
Vs= V1 + V2 + V3
Это основное соотношение известно как закон Кирхгофа для напряжений. Закон этот чрезвычайно полезен при осуществлении расчетов для последовательных схем. При использовании данного соотношения различными способами можно легко выполнять анализ и разработку последовательных схем.
Токоограничивающие резисторы
Примером использования закона Кирхгофа является расчет последовательных гасящих резисторов. Последовательный гасящий резистор — это просто резистор, соединенный последовательно с некоторым устройством с той целью, чтобы понизить напряжение, прилагаемое к данному устройству. Такой резистор называется также токоограничивающим резистором. Часто оказывается необходимым, например, включать лампу накаливания от источника высокого напряжения. Чтобы избежать повреждения устройства при перенапряжении, резистор включается последовательно с устройством, чтобы погасить излишнюю величину напряжения (см. рис. 4-2). Кроме того, может оказаться необходимым включить трехвольтовую лампочку от батареи питания 12 В. Если приложить все напряжение 12 В к лампочке, последняя перегорит. Однако при включении последовательно с лампочкой резистора с правильно выбранным
сопротивлением на резисторе создастся падение излишнего напряжения 9 вольт, тогда как для лампочки останется только 3 вольта необходимого ей напряжения. Короче говоря, резистор выбирается для ограничения тока через лампочку до максимально безопасной величины.
Рис. 4-2.
Краткое содержание
В данном эксперименте Вы убедитесь, что общее сопротивление последовательной схемы равно сумме отдельных сопротивлений включенных последовательно резисторов. Затем Вы проверите справедливость закона Кирхгофа для напряжении. Наконец, Вы рассчитаете последовательный гасящий резистор для светоизлучающего диода.
Рис. 4-3.
ПРОЦЕДУРА
1. Используя значения, указанные на рис. 4-3, рассчитайте общее сопротивление схемы.
Rт= _____Ом (вычисленное значение)
2. Соберите схему, показанную на рисунке 4-3.
3. Используя Ваш мультиметр, измерьте общее сопротивление схемы.
Rт= ______Ом (измеренное значение)
4. Сравните Ваши вычисленное и измеренное значения и объясните возможную разницу.
Рис. 4-4.
5. Подключите источник питания 9 В к схеме (см. рис. 4-4).
6. Используя значение общего сопротивления, которое Вы подсчитали ранее, рассчитайте и запищите ожидаемый ток в цепи при приложенном напряжении 9 В. I =_____мА
7. Теперь, используя закон Ома, вычислите и запишите напряжение, падающее на каждом резисторе.
V1= _______ В
V2 = _______ В
V3= _______ В
8. Теперь вычислите и запишите сумму отдельных падений напряжения.
Vs=v1+v2+v3___В
9. Используя Ваш мультиметр, измерьте падение напряжения на каждом резисторе. Не забывайте, что Вы измеряете напряжения постоянного тока, и Вам следует прикасаться испытательными выводами мультиметра к выводам резистора в корректном направлении, чтобы получить правильные в отношении полярности показания. Заметьте полярности для падений напряжения в схеме на рисунке 4-4. Запишите Ваши измеренные падения напряжения, а затем вычислите их сумму.
V1=_____В
V2=______В
V3=____в
Vs=______В
10. Сравните Ваши измеренные и расчетные значения для падений напряжения и общего напряжения. Равна ли сумма падений ли напряжения напряжению источника? 11. Обратитесь к рисунку 4-5. Здесь показан светоизлучающий диод, который должен запитываться от источника питания 9 В. Ваша задача определить сопротивление последовательного гасящего резистора R1. В проводящем состоянии светоизлучающего диода на нем падает напряжение приблизительно 2 В. Ток величиной 15 мА требуется для обеспечения умеренной яркости. Рассчитайте сопротивление потребного последовательного гасящего резистора. Запишите это значение сопротивления. R1= ________ Ом
Рис. 4. 5.
12. Среди имеющихся в Вашей лаборатории резисторов выберите резистор с сопротивлением, ближайшим по величине к найденному Вами. Затем соберите схему, показанную на рисунке 4-5. Обеспечьте соблюдение полярности как для подключения батареи, так и для выводов светоизлучающего диода. При этом отрицательный вывод источника питания должен быть подключен к катодному выводу светодиода (этот вывод идентифицируется плоской стороной на корпусе диода). В символе светодиода стрелка является анодом, тогда как прямая черта соответствует катоду.
13. Если Вы рассчитали и выбрали корректное сопротивление резистора, должен загореться светоизлучающий диод. Измерьте падения напряжения на резисторе R1 и на светоизлучающем диоде (LED).
V1=______В
Vled=_____В
Vs=_______В
14. Равна ли сумма падений напряжения напряжению источника питания? Сравните измеренные и рассчитанные значения. Имеются ли какие-либо отличия? Объясните разницу, если таковая имеется.
ОБЗОРНЫЕ ВОПРОСЫ
1. Два резистора (R1 и R2) соединены последовательно. Сопротивление R1 = 68 Ом. Общее сопротивление R = 150 Ом. Каково значение сопротивления R2?
а) 28 Ом,
б) 82 Ом,
в) 86 Ом,
г) 218 Ом.
2. В последовательной схеме падения напряжений на резисторах равны V1 = 2.5 В, V2, = 1,8 В, V3 = 3,4 В и V4 = 6, 9 В. Каково напряжение источника питания?
а) 10, 3 В,
б) 12, 1 В,
в) 12, 8 В,
г) 14, 6 В.
3. Справедливо ли высказывание: «Ток через все последовательно соединенные резисторы в схеме одинаков»?
а) да,
б) нет.
4. Лампочка напряжением 6 В потребляет ток 0, 15 А. Чтобы подключить ее к источнику питания 15В, Вам требуется последовательный гасящий резистор:
а) 33 Ом,
б) 50 Ом,
в) 60 Ом,
г) 120 Ом.
5. В последовательную цепь включены резисторы 180 Ом, 2, 7 кОм, 5, 6 кОм и 6, 8 кОм. На каком из резисторов будет наименьшее падение напряжения?
а) 180 Ом,
б) 2, 7 кОм,
в) 5, 6 кОм,
г) 6, 8 кОм.
riostat.ru









Поделиться с друзьями: