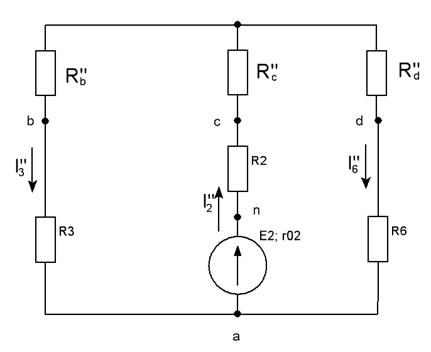
Для нахождения сопротивлений на индуктивном и емкостном элементах необходимо вычислить круговую частоту: ω = 2πf=2∙3.14∙100 = 628 c-1 Найдем комплексы полных сопротивлений ветвей схемы: Z1 = R1 + j( XL1 – XC1 ) = R1 + j( ωL - ) = 31 + j( 628·64·10-3 - ) = = 31 + j29,919 = 43,083∙e = 43,083∙e Ом Z2 = R2 + jXL2 = R2 + j(ωL2) = 40 + j(628·64·10) = 40 + j40,192 = = 56,704∙e = 56,704∙e Ом Пусть, ψu = 0°. Тогда, I1 = === 4,642·e= 4,642·(cos(-43,983°) + + j∙sin(-43,983°)) = 4,642·(0,72 - j∙0,694) = 3,342 – j∙3,222 А I2 = === 3,527∙e= 3,527∙(cos(-45,137°) + j∙sin(-45,137°)) = 3,527∙(0,705 - j∙0,709) = 2,487 - j∙2,501 А По первому закону Кирхгофа: I = I1 + I2 = 3,342 – j∙3,222 + 2,487 - j∙2,501 = 5,829 - j∙5,723 = 8,169∙e = 8,169∙eА а) Показания амперметров (показывают только действующее значение тока): pA1 = I1 = 4,642 А pA2 = I2 = 3,527 А pA3 = I = 8,169 А б) Показание фазометра. Фазометр показывает разность фаз между током и напряжением: pφ =φ = ψu – ψi = 0° - (-44,474°) = 44,474° в) Показание ваттметра. Так как ваттметр показывает только активную мощность, то для приведенной схемы включения ваттметра: pW = Re[S] = Re[U∙I*] = 200∙5,829 = 1165,8 Вт. г) Показание вольтметра: Определяем по второму закону Кирхгофа (рис.15.): UV + UR1 – UL2 = 0 UV = I2jωL2 – I1R1 = (2,487 - j∙2,501)∙j∙628∙64∙10-3 - - (3,342 – j∙3,222)∙31 = j∙99,9575 + 100,52 -103,602 + + j∙99,882 =-3,082 + j∙199,8395 = 199,86∙e В pV = UV = 199,86 В. Рис.15. Запишем уравнение баланса для полноймощности: , где- сопряженный комплексный ток. Sист = 200∙(5,829 + j∙5,723) = 1165,8 + j∙1144,6 ВА, где Pист = Re[Sист] = 1165,8 Вт Qист = Im[Sист] = 1144,6 ВАр ∑Sпр = ∑Pпр + ∑jQпр ∑Sпр = I12∙Z1 + I22∙Z2 = (4,642)2∙(31 + j29,919) +(3,527)2∙(40 + j40,192) = 667,993 + + j∙644,7 + 497,589 + j∙499,978 = 1165,582 + j∙1144,678 ВА Pпр = Re[Sпр] = 1165,582 Вт Qпр = Im[Sпр] = 1144,678 ВАр Так какPист = Pпр и Qист = Qпр Баланс мощностей соблюдается токи найдены верно. Т.к. показание фазометра φ=44,4740>0 ,следовательно,цепь носит активно- индуктивный характер и для того,что бы повысить коэффициент мощности до 0,98 включаемпараллельно емкостной элемент. Рис.16. По первому закону Кирхгофа: I1вх = I2вх + Iс , где I1 вх – токдокомпенсации,I2 вх– токпослекомпенсации. Iр = Iа∙tgφ φ1=44,474° φ2 = arccos(0,98) = 11,478° Iс = I1вх - I2вх = Iа∙(tgφ1 – tgφ2) = , Iа = C = == 36,141мкФ Рис.17. 2.5. Построение векторных диаграмм токов и напряжений в одной системе координат Определим напряжения на катушках, резисторахи конденсаторе: UL1 = I1∙j∙XL1 = (3,342 – j∙3,222)∙j∙40,192 =129.499 + j∙134,322 = 186,58∙eВ UL2 = I2∙j∙XL2 = (2,487 - j∙2,501) ∙j∙40,192 = 100,52 + j∙99,958 = 141,76∙eВ UR1 = I1∙R1 = 4,642·e∙31 = 143,902·eВ UR2 = I2∙R2 = 3,527∙e∙40 = 141,08∙eВ UC1 = - I1∙j∙XC1 = -(3,342 – j∙3,222)∙j∙10,273 = -33,0996 -j∙34,332 = 47,689∙eВ. Масштаб: MI: 0,05 A : 1мм MU: 2В : 1мм Рис.18. ЧАСТЬ 3 РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ Задание: 1.Составить схему включения приемников. 2.Определить комплексы действующих значений фазных и линейных токов. 3.Составить схему включения ваттметров для измерения активной мощности каждого трехфазного приемника. 4.Рассчитать активную, реактивную и полную мощность каждого приемника. 5.Построить векторные диаграммы токов и напряжений для каждого приемника. Рис.19. Схема соединения приёмников: звезда с нулевым проводом Дано: Нагрузка: несимметричная U=380 В Ra=101 Ом Rb=65 Ом Rс=73 Ом La=0 Lb=0 Lc=97 мГн Ca=87 мкФ Cb=93 мкФ Cc=0 Схема соединения приёмников: треугольник Дано: Нагрузка: симметричная U=380 В R=108 Ом L = 76 мГн f=50 Гц studfiles.net По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности. а) Определяем частные токи от ЭДС Е1, при отсутствии ЭДС Е2, т.е. рассчитываем цепь по рис. 1.2. Рис 1.2. Схема цепи при выведенном E2 Показываем направление частных токов при ЭДС Е1 и обозначаем буквой I с одним штрихом(‘). Решаем задачу методом "свёртывания". Преобразовываем треугольник сопротивлений R2-R3-R4 в эквивалентную звезду Rb/- Rc/- Rd/. Рис 1.2.2 Преобразованная схема при выведенном E2 б) определяем частные токи от ЭДС Е2, при отсутствии ЭДС Е1, т.е. рассчитываем цепь по рис.1.3 Показываем направление частных токов при ЭДС Е2 и обозначаем их буквой I с двумя штрихами (“). Рис 1.3. Схема цепи при выведенном E1 Рис 1.3.2 Преобразованная схема при выведенном E1 Вычисляем токи ветвей исходной цепи (рис. 1.1), выполняя алгебраическое сложение частных токов, учитывая их направление: Составить баланс мощностей для заданной схемы. Источники Е1 и Е2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источником совпадают. Баланс мощностей для заданной цепи запишется так: Подставляем численные значения и вычисляем: С учетом погрешности расчетов баланс мощностей получился. Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить. Расчет токов ветвей обоими методами с точностью до трех знаков после запятой практически одинаков. Определить ток во второй ветви методом эквивалентного генератора. Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2 служит источником электрической энергии, т.е. генератором). Получается схема замещения (рис. 1.4.1). Рис. 1.4.1. Схема эквивалентного генератора для 2-й ветви На схеме искомый ток I2 определим по закону Ома для замкнутой цепи: I2=Eэ/(R2+Rэ) Где Еэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Еэ=Uхх, Rэ - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рис.1.4.2), т.е. при отключенном потребителе R2. Производим расчет напряжения в месте отключения R2. Рис. 1.4.2. Эквивалентная схема при холостом ходе ветви 2 Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис. 1.4.1), при этом ЭДС из схемы исключается, а внутренне сопротивление этих источников в схеме остаются. Используем преобразование схемы, проведенное при расчетах в п. 1.3.б. Вычисляем эквивалентное сопротивление схемы (рис. 1.4.2) относительно зажимов a и c. Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви: т.е. ток в этой ветви получился практически таким же, как и в пунктах 2 и 3. Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Возьмем контур acbda. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка a. Потенциал этой точки равен нулю φa=0 (рис. 1.1) Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки a. Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивление контура в той последовательности, в которой производим обход контура, прикладывая, сопротивления друг, к другу, по оси ординат потенциалы точек с учетом их знака. Рис.1.4.3 Потенциальная диаграмма замкнутого контура Заключение В данной курсовой работе я проводил анализ электрического состояния линейной цепи постоянного тока. Расчеты производил различными методами: по I и II закону Кирхгофа, методом наложения, методом эквивалентного генератора, используется метод расчета электрической цепи. Работа над данной курсовой работой позволяет решить следующие задачи: закрепление теоретических знаний, полученных на лекционном курсе; развитие творческого технического мышления; усвоение методики выполнения расчетов; развитие навыков по работе со справочной литературой; развитие умения составления и оформления пояснительной записки; Библиографический список 1. Касаткин А.С. Электротехника: Учебник. – М.: Высшая школа, 2000. 2. Прянишников В.А. Теоретические основы электротехники: Курс лекций. – СПб, 2000. 3. Рекус Г.Г., Белоусов А.И. Сборник задач и упражнений по электротехнике и основам электроники: Учебное пособие. – М.: Высшая школа, 2001. 4. Левашов Ю.А. Электротехника и электроника: Рабочая программа, контрольные работы, курсовая работа и методические указания для студентов заочной формы обучения специальности "Вычислительные машины, комплексы, системы и сети". – Владивосток: Издательство ВГУЭС, 2002. . 5. Прянишников В.А., Петров Е.А., Осипов Ю.М. Электротехника и ТОЭ в примерах и задачах: Практическое пособие. – СПб. 2001. 6. Иванов И.И., Лукин А.Ф., Соловьев Г.И. Электротехника: Основные положения, примеры и задачи. – СПб. 2002. stydopedia.ru R1=10Ом R2=15 Ом R3=15 Ом
С1=200мкФ=2*10-4Ф С2=100мкФ=10-4Ф
L1=75мГн=75*10-3Гн L2=75мГн=75*10-3Гн L3=100мГн=10-4Гн
u=660sin(ωt-30) f=50Гц I-? 4Решение:
3 4 XL1=2πfL1=2*3.14*50*75*10-3=24Ом XL2=2πfL2=2*3.14*50*75*10-3=24Ом XL3=2πfL3=2*3.14*50*0.1=31Ом
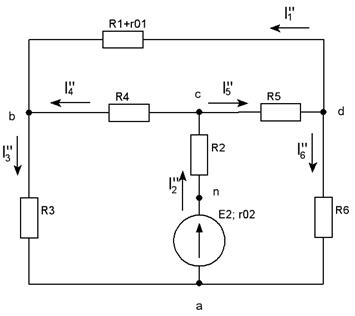
XC2===32Ом1. Определение токов во всех ветвях схемы по законам Кирхгофа без учёта индуктивной связи катушек =468В Произвольно выбираем направления токов в схеме. Произвольно выбираем направление обхода контуров для составления уравнений по второму закону Кирхгофа. Составляем уравнения по законам Кирхгофа: По первому закону Кирхгофа имеем: I1-I2-I3=0 (узел 1) I2+I3-I4-I5=0 (узел 2) По второму закону Кирхгофа имеем: XC1 I2- XL1 I3=0 (1 контур) R1I1+ XL1 I3+ XL2 I4+R2I4=-U (2 контур) XL3 I5+ XC2 I5+R3I5-R2I4- XL2 I4=0 (3 контур)
Выразим систему уравнений в матричной форме I1 - I2 - I3 + 0 + 0 = 0 0 + I2 + I3 - I4 - I5 = 0 0 + XC1I2 - XL1I3 + 0 + 0 = 0 R1I1 + 0 + XL1I3 +(XL2 + R2)I4 +0 = -U 0 + 0 + 0 – (R2 + XL2)I4 +(XL3 + XC2 + R3)I5 = 0 Матричное уравнение цепи [Z][I]=[U], где [Z] –квадратная матрица сопротивлений; [I] - матрица – столбец комплексных токов; [U] - матрица – столбец ЭДС.
Подставляем численные значения параметров схемы в матричное уравнение: == Решив матричное уравнение, получим токи: I1=18А I2=11А I3=7 А I4=12А I5=6А По второму закону Кирхгофа имеем: XC1 I2- XL1 I3=0 R1I1+ XL1 I3+ XL2 I4+R2I4=-U XL3 I5+ XC2 I5+R3I5-R2I4- XL2 I4=0 Откуда получаем: I3= XC1 I2 / XL1 I1= I2 + I3 R1(I2 + I3 )+ XC12I2 / XL1 + (XL2 +R2)I4 =-U XL2 I4 = (XL3 + XC2 + R3)I5 R1I2 + R1 R1+ XC12I2 / XL1 +(XL2 +R2) (XL3 + XC2 + R3)I5=-U
Решая полученные уравнения найдем токи: R1=10Ом, R2=15 Ом, R3=15 Ом, XL1=24Ом, XL2=24Ом, XL3=31Ом, XC1=16Ом, XC2=32Ом U=468В
Потенциал узла "4" принимаем равным нулю φ2 = 0. Мощность источника
Мощность нагрузки: Рн= XC1I22 - XL1I3 2+ XL2I4 2 + (XL3 + XC2 + R3)I5 2 =3240Вт
3240Вт=3240Вт Pи= Рн =410
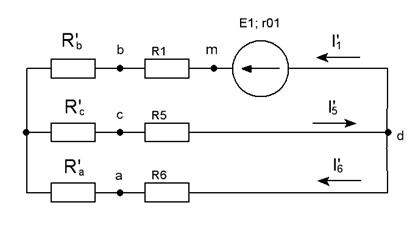
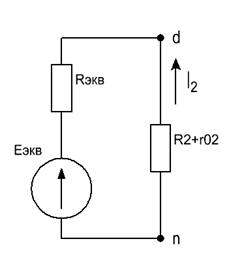
Для участка цепи 2-3, где последовательное соединение ==316 birmaga.ru Теорема об эквивалентном источнике ЭДС (теорема Тевенина): Любой линейный активный двухполюсник можно заменить эквивалентным источником ЭДС Eэкв с внутренним сопротивлением Rэкв , при этом ЭДС этого источника равно напряжению на зажимах (ab) в разомкнутой ветви, в которой необходимо определить ток, т.е. напряжению холостого хода Еэкв=Uab хх. Расчет схемы в режиме холостого хода для определения Eэкв производится любым известным способом. Внутреннее сопротивление Rэкв эквивалентного источника ЭДС равняется полному сопротивлению двухполюсника при выключенных источниках (источники ЭДС заменяются короткозамкнутыми участками цепи, а источники тока - разрывами цепи). Тогда схема (рис. 2.1) преобразуется в схему на рис. 2.2 и искомый ток определяется из формулы (2.1). Рассмотрим часть схемы, подключенной к ветви с током I1 (обведенной штриховой линией на рис. 2.1) в качестве эквивалентного источника ЭДС Еэкв с внутренним сопротивлением Rэкв. Исключим ветвь с R1 и рассмотрим оставшуюся часть схемы рис. 2.3. Рис. 2.1 Рис. 2.2 (2.1) По теореме Тевенина Еэкв=Uab хх. Как видно на рис. 2.3 разность потенциалов между точками а и b определяется падением напряжения на сопротивлениях R5, R3 и на источнике E3: Uab хх= I′5R5 + I′3R3 + E3 . (2.2) Рис. 2.3 Токи I′5 и I′3 можно найти методом контурных токов или любым другим методом расчета линейных электрических схем. По методу контурных токов получаем систему из двух уравнений: (2.3) решая которую находим токи I′5 и I′3, затем рассчитываем ЭДС эквивалентного генератора (2.2). Для нахождения внутреннего сопротивления эквивалентного генератора исключим источники из схемы: Рис. 2.4 Теперь необходимо преобразовать треугольник сопротивлений acd в звезду: Рис. 2.5 (2.4) . После преобразования схема принимает вид: Рис. 2.6 Теперь Rэкв находится из формулы: . (2.5) Вычислив ток I1, по формуле (2.1) можно сравнить его со значением тока в первой ветви, полученным по методу контурных токов (Задание 1). Рассмотрим схему: Рис. 3.1 Расставим номера узлов. Потенциал нулевого узла примем равным 0. Потенциалы остальных узлов U10, U20, U30 рассчитываются относительно нулевого. Уравнения по методу узловых потенциалов составляются на основе первого закона Кирхгофа. В левые части каждого из них входят: 1. Произведение полной проводимости узла на его узловой потенциал со знаком плюс. Например, для первого узла получаем . (3.1) 2. Произведения проводимостей ветвей, подходящих к данному узлу на соответствующий узловой потенциал со знаком минус. В уравнение для первого узла добавляется . (3.2) В правые части уравнения входят комплексные амплитуды источников ЭДС с коэффициентами, равными их внутренним проводимостям и источники тока в соответствующих ветвях. Знаки перед Е и I отрицательны, если ориентирные стрелки направлены от узла, и положительны в противоположном случае. Например, к первому узлу подходят источники E5, Iк5, E6 и Iк6. Все они направлены от узла, поэтому будут входить в правую часть уравнения со знаком «минус»: . (3.3) Окончательное уравнение по методу узловых потенциалов для первого узла имеет вид: . (3.4) Аналогично записываем уравнения для второго и третьего узлов: , (3.5) . Решая совместно систему из трех уравнений (3.4), (3.5) находим потенциалы U10, U20, U30. Разность потенциалов, например, между узлами 2 и 3 всегда можно выразить, через узловые потенциалы U20 и U30: U23 = U20-U30; U32 =U30-U20 и т.д. Найдем токи в ветвях I1, ... I6. Ток I1 течет от нулевого ко второму узлу. Следовательно, по закону Ома получаем: I1=U02/R1=-U20/R1. Аналогично записывается выражение для токов I2, I3, I4: I2 = U23/R2 = (U20-U30)/R2; I3 = U30/R3; (3.6) I4 = U01/R4 = -U10/R4. В ветвях с источником энергии необходимо учитывать падение напряжения на них: ; (3.7) . studfiles.net Для электрической цепи, изображенной на рис. 1.31, выполнить следующее: 1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы; 2) определить токи во всех ветвях схемы, используя метод контурных токов; 3) определить токи во всех ветвях схемы на основании метода наложения; 4) составить баланс мощностей для заданной схемы; 5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить; 6) определить ток во второй ветви методом эквивалентного генератора; 7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. 8) результаты расчетов занести в соответствующую таблицу. Дано: Е1= 40 В, Е2 = 60 В, R1 = 18 Ом, R2 = 36 Ом, R3 = 16 Ом, R4 = 24 Ом, R5 = 40 Ом, R6 = 34 Ом, r01 = 2 Ом, r02 = 4 Ом. Определить: I1, I2, I3, I4, I5. Рис.1.31 1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях. Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразова- ний схемы и пригоден для расчета любой цепи. При расчете данным методом произвольно задаем направление токов в ветвях I1, I2, I3, I4, I5. Составляем систему уравнений. В заданной цепи пять ветвей, значит, в системе должно быть пять уравнений (m = 5). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n - 1) независимых уравнений. В нашей цепи три узла (А, В, С), значит, число уравнении n - 1 = 3-1 = 2. Составляем два уравнения для любых 2-х узлов, например, для узлов В и С. узел В: I1 + I2 = I4 узел С: I3 + I5 = I2 Всего в системе должно быть пять уравнений. Два уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие. Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа. Контур АДСВА - обход по часовой стрелке: Е2 - E1 = I2 (R2 + r02) – I1 (R1 + r01) + I3(R3 + R6) Контур ABA'A - обход по часовой стрелке: E1 = I1(R1+r01)+I4R4 Контур А'СВА' — обход против часовой стрелки: E2 = I2(R2 + r02)+I4R4 + I5R5 ЭДС в контуре берется со знаком “+”, если направление ЭДС совпадает с обходом контура, если не совпадает – знак “-”. Падение напряжения на сопротивлении контура берется со знаком “+”, если направление тока в нем совпадает с обходом контура, со знаком “-” если не совпадает. Мы получили систему из пяти уравнений с пятью неизвестными: Решив систему, определим величину и направление тока во всех ветвях схемы. Если при решении системы ток получается со знаком “-” значит его действительное направление обратно тому направлению, которым мы задались. 2) Определить токи во всех ветвях схемы, используя метод контурных токов. Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1. Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной. Итак, в заданной цепи (рис. 1.38) можно рассмотреть три контура-ячейки (АДСВА, ABA'А, А'СВА') и ввести для них контурные токи Ik1, Ik2, Ik3. Контуры-ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления. При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур - ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим: стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3. в контурах - ячейках. Направление обхода контуров принимаем таким же; составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей. Подставляем в уравнение численные значения ЭДС и сопротивлений. или Сократив первое уравнение на 4, второе – на 4,третие – на 10, получим: Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ1, Δ2, Δ3. Вычисляем контурные токи: Действительные токи ветвей: 3) Определить токи во всех ветвях схемы на основании метода наложения. По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности. а) Определяем частные токи от ЭДС E1, при отсутствии ЭДС Е2, т. е. рассчитываем цепь по рис. 1.32. Показываем направление частных токов от ЭДС Е1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания" Рис. 1.32 Ток источника Применяя формулу разброса и 1-й закон Кирхгофа, вычисляем токи ветвей: б) Определяем частные токи от ЭДС E2 при отсутствии ЭДС Е1,т.е. рассчитываем простую цепь по рис. 1.33. Показываем направление частных токов от ЭДС Е2 и обозначаем их буквой I с двумя штрихами (I"). Рассчитываем общее сопротивление цепи: Рис.1.33 Вычисляем ток источника: Применяя форму разброса и 1-й закон Кирхгофа, вычисляем токи ветвей: Вычисляем токи ветвей исходной цепи (рис. 1.31), выполняя алгебраическое сложение частных токов, учитывая их направление: 4) Составить баланс мощностей для заданной схемы. Источники E1 и Е2 вырабатывают электрическую энергию, т. к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так: Подставляем числовые значения и вычисляем С учетом погрешности расчетов баланс мощностей получился. 5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить. Ток в ветви Метод расчета I1,A I2,A I3,A I4,A I5,A метод контурных токов метод наложения 0,624 0,625 0,522 0,522 0,232 0,232 1,146 1,147 0,290 0,290 Расчет токов ветвей обоими методами с учетом ошибок вычислений практически одинаков. 6) Определить ток во второй ветви методом эквивалентного генератора. Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2служит источником электрической энергии, т. е. генератором). Получается схема замещения (рис. 1.34) На схеме искомый ток I2 определим по закону Ома для замкнутой цепи: , где Еэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ = Uхх. rэ - внутреннее сопротивление эквивалент- Рис.1.34 ного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.35), т. е. при отключенном потребителе R2 от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину: Зная Iхх, величины сопротивлений и ЭДС, Рис. 1.35 в схеме можно определить Uхх как разность потенциалов между клеммами а и б. Для этого потенциал точки б будем считать известным и вычислим потенциал точки а. тогда Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис. 1.36), при этом ЭДС Е2 и E1 из схемы исключается, а внутренние сопротивления этих источников r01 и r02 в схеме Рис. 1.36 остаются. Вычисляем эквивалентное сопротивление схемы (рис. 1.36) относительно зажимов а и б. Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви: т. е. ток в этой ветви получился таким же, как и в пунктах 2 и 3. 7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Возьмем контур АДСВА. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю φА=0 (рис. 1.31). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А. 0 - проверочная точка. Строим потенции- альную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикла- дывая сопротивления друг к другу, во оси ординат - потенциалы точек с учетом их знака. studfiles.net Анализ состояния электрических цепей Рисунок 1.2 Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений. Итак, в заданной цепи можно рассмотреть три контурных - ячейки и ввести для них контурные токи I11, I22... Анализ электрического состояния линейных и нелинейных цепей постоянного и переменного токов Определить токи во всех ветвях схемы, используя метод контурных токов. Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в схеме на n1... Анализ электрического состояния линейных электрических цепей постоянного тока I2-I5-I3=0; I2-I5-I3=0; I5+I6-I7=0; I5+I6-I7=0; I7-I1-I2-I4=0; I7-I1-I2-I4=0; E2-E1=R3I3-(R5+r01) I5+(R6+r02) I6; 10=53I6-46I5+22I3; E1=R2I2+(R5+r01) I5+R7I7; 0=55I7+27I2+46I5; 0=R4I4-R3I3-R2I2; 0=33I4-22I3-27I2; 0=I1R1-I4R4; 0=16I1-33I4; Решив данную систему, мы найдем истинные токи в ветвях... Анализ электрического состояния линейных электрических цепей постоянного тока a) Нахождение частных токов при исключении источника питания Е2: Преобразовываем схему (рис.1.0) в эквивалентные схемы на (рис.1.2), (рис.1.3) и (рис.1.4) без Е2... Анализ электрического состояния линейных электрических цепей постоянного тока По формуле I=U/R строим ВАХ линейных элементов совмещенной с ВАХ нелинейных элементов (рис.2.2). I3=U/R3=200/27=7,4 A.; I4=U/R4=200/30=6,7 A.; Элементы R4 и НЭ2 соединены последовательно... Анализ электрического состояния линейных электрических цепей постоянного тока Э=Щ/ZЭКВ=1,1879e-j65,5 A; Э1=Э2=Э=1,1879e-j65,5 A; Щ34=ЭZ34=20,8076e-j65,8 A; Э3=Щ34/Z3=0,6935e-j66,9 A; Э4=Щ34/Z4=0,495e-j63... Анализ электрической цепи синусоидального тока Для расчёта токов в ветвях воспользуемся методом междуузлового напряжения... Применение матричных методов для анализа установившихся режимов электрических систем 1. Матричная форма записи: Запишем первый закон Кирхгофа в матричной форме:... Проект ТЭЦ мощностью 500 МВт Данный подход основывается на учете экономических интересов предприятий и учитывает изменение его основных хозрасчетных показателей... Расчет линейных электрических цепей постоянного и переменного тока Метод контурных токов основан на использовании второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на... Расчет линейных электрических цепей постоянного тока Определить токи во всех ветвях схемы, используя метод контурных токов. Определить токи во всех ветвях схемы на основании метода наложения. Составить баланс мощностей для заданной схемы. Результаты расчетов токов по пунктам 1.2. и 1.3.... Расчет линейных электрических цепей при негармоническом воздействии Запишем систему уравнений для метода контурных токов в общем виде содержащей три независимых контура: Запишем собственные комплексные сопротивления контуров: Ом Ом Ом Запишем взаимные комплексные сопротивления контуров: Ом Ом... Расчет электрических цепей Выберем направления токов в ветвях и выберем направления контурных токов I11, I22, I33 (контурные токи текут по часовой стрелке), в контурах abca, acda, bcdb соответственно. Количество контуров определяется из формулы: число ветвей... Расчет электрической цепи постоянного тока и напряжения Согласно своему варианту даны следующие исходные параметры: E1=21 В; E2=4 В; E3=10 В; R1=5 Ом; R2=7 Ом; R3=2 Ом; R4=8 Ом; R5=1 Ом; R6=1 Ом. Используется схема, показанная на рисунке 13... Расчёт токов короткого замыкания ... fis.bobrodobro.ru Задача 1. Для схемы, изображенной на рисунке требуется: Исходные данные: L = 30 мГн, С = 50 мкФ, R = 8 Ом, E = 24 В Схема электрической цепи Решение: 1. Расчет классическим методом. После размыкания рубильника схема будет иметь следующий вид: Для данной схемы, исходя из законов Кирхгофа, запишем систему уравнений: Получим систему алгебраических уравнений для свободных составляющих переходных токов: заменяем дифференцирование умножением на p, интегрирование – делением на p: Решение этой системы будет нетривиальным, если определитель данной системы будет равняться нулю. После подстановки соответствующих значений для RLC, получим следующее квадратное уравнение: Найдем корни этого уравнения: Из расчетов видно, что корни характеристического уравнения действительные, причем следовательно, переходной процесс носит апериодический характер. В данном случае ток в индуктивности и напряжение на емкости определяются следующим образом: Определим принужденные составляющие: Рассмотрим послекоммутационную схему: В этой цепи индуктивность закорочена, ветвь с емкостью разорвана. Из схемы видно, что Найдем независимые начальные условия: Рассмотрим докоммутационную схему: В этой цепи индуктивность закорочена, ветвь с емкостью разорвана. Напряжение на емкости определяется напряжением источника ЭДС: Ток в цепи определяется следующим образом: По законам коммутации получаем выражения для момента размыкания: Значение для Определим зависимые начальные условия: Из 2-го уравнения системы (*) следует: Так как Рассмотрим уравнения (**) при t = 0: Подставляя значения для Продифференцируем уравнения (**), принимая t = 0 : Подставляя значения для производных и для Таким образом получаем системы уравнений для нахождения постоянных интегрирования: Подставляя найденные значения для постоянных интегрирования в уравнения (**), получим: Найдем напряжение на катушке: Исходя из 2-го уравнения системы (*) следует, что: Исходя из 3-го уравнения системы (*) следует, что: Таким образом, мы получили следующие зависимости: Проверим правильность расчета по 1-му закону Кирхгофа: Следовательно, расчет правильный. 2. Расчет операторным методом. Найдем независимые начальные условия: Рассмотрим докоммутационную схему: В этой цепи индуктивность закорочена, ветвь с емкостью разорвана. Напряжение на емкости определяется напряжением источника ЭДС: Ток в цепи определяется следующим образом: По законам коммутации получаем выражения для момента размыкания: Рассмотрим операторную схему замещения: Для определения изображения тока в катушке индуктивности ( При данном разбиении на контуры изображение тока в катушке индуктивности будет равен току 1-го контура: Система уравнений по методу контурных токов имеет вид: Найдем Подставив значения для Определим корни знаменателя: Используя теорему разложения, найдем оригинал тока В нашем случае: Таким образом: Расчет классическим методом дал тот же результат, следовательно, расчет правильный. График изменения напряжения на конденсаторе: Задача 2. Для схемы, изображенной на рисунке требуется: 1. Определить закон изменения напряжения на конденсаторе. Исходные данные: С = 50 мкФ, R = 8 Ом, Em = 36 В, f=30o , Схема электрической цепи Решение: Найдем независимые начальные условия: Рассмотрим докоммутационную схему: Исходя из схемы видно, что напряжение на конденсаторе равно напряжению источника синусоидальной ЭДС: По закону коммутации: Так как коммутация происходит в момент времени t = 0, то Определим принужденные составляющие: Рассмотрим послекоммутационную схему: Здесь Найдем эквивалентное сопротивление относительно источника ЭДС: По закону Ома принужденный ток в 1-ой ветви равен: По правилу разброса токов найдем принужденный ток в 3-ей ветви: Найдем принужденное напряжение на конденсаторе: Или После размыкания рубильника схема будет иметь следующий вид: По законам Кирхгофа можно записать: Получим систему алгебраических уравнений для свободных составляющих переходных токов: заменяем дифференцирование умножением на p, интегрирование – делением на p: Решение этой системы будет нетривиальным, если определитель данной системы будет равняться нулю. Таким образом, свободная составляющая напряжения на конденсаторе имеет вид: Переходное напряжение определяется по формуле: В момент времени t = 0 откуда Значит: vunivere.ruРасчет токов во всех ветвях и напряжения на реактивных элементах электрической цепи. Определить токи во всех ветвях схемы
2.1.Определение комплексных действующих значений токов в ветвях схемы
2.2. Определение показаний приборов
2.3. Составление баланса активных, реактивных и полных мощностей
2.4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента х
Определить токи во всех ветвях схемы на основании метода наложения.
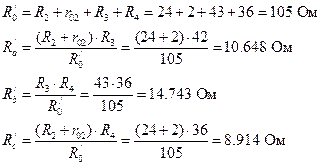
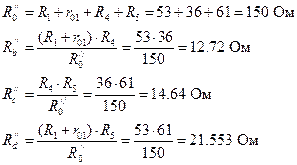
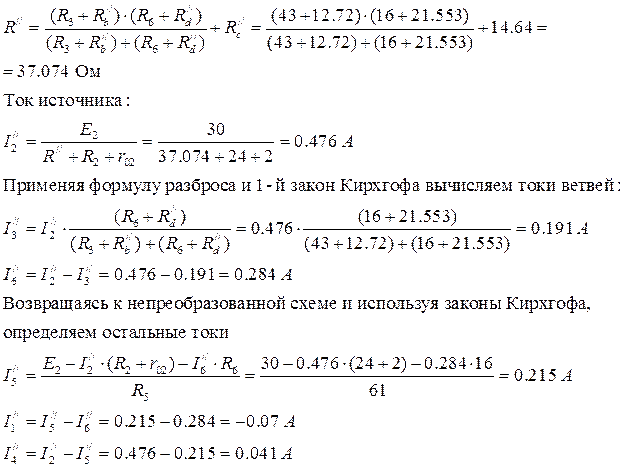
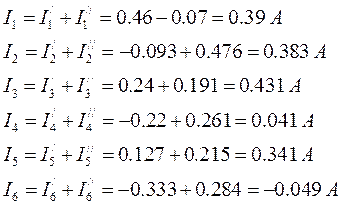
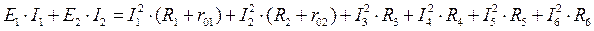
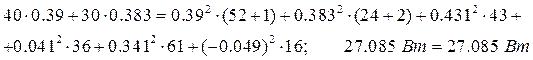
Ток в ветви
Метод расчёта
I1
A
I2
A
I3
A
I4
A
I5
A
I6
A
Метод контурных токов
Метод наложения
0.39
0.39
0.383
0.383
0.431
0.431
0.041
0.041
0.341
0.341
-0.049
-0.049
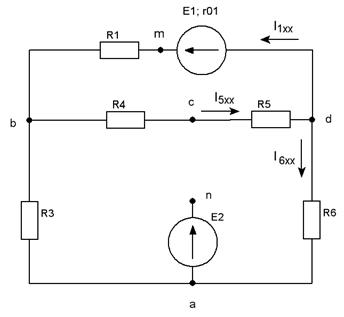
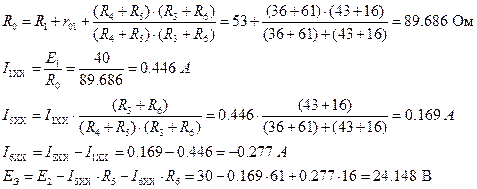
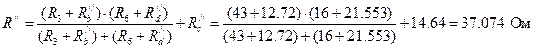
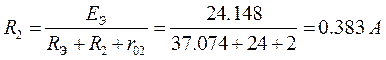
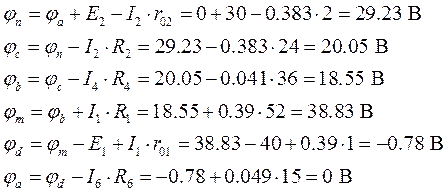
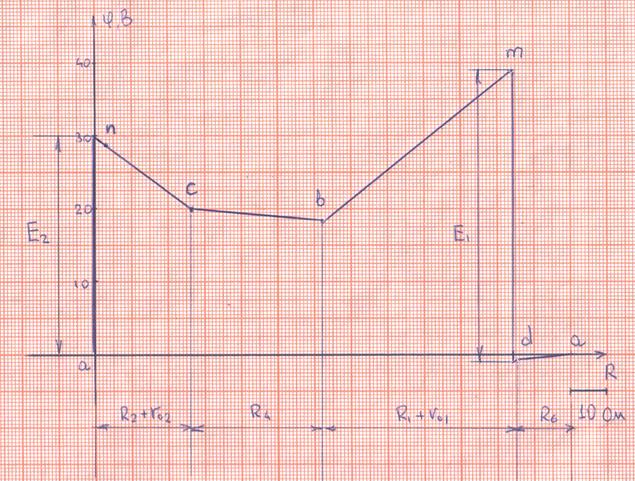
1. Определение токов во всех ветвях схемы по законам Кирхгофа без учёта индуктивной связи катушек
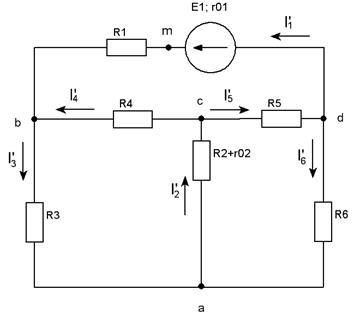
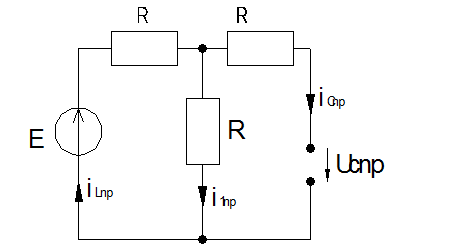
Для электрической цепи, изображенной на рисунке, решить следующие задачи:
Определение сопротивлений катушек и конденсаторов: Дано:
I1,А
I2,А
I3,А
I4,А
I5,А
Закон Кирхгофа
18
11
7
12
6
Метод контурных токов
18
11
7
12
6
Метод узловых потенциалов
17,7
10,8
7,1
11,9
5,9
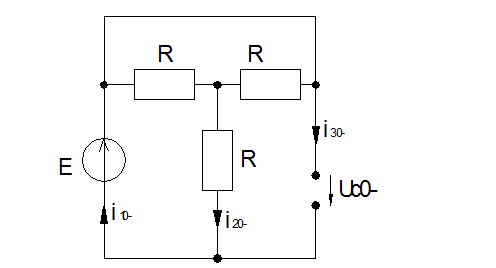
Для участка цепи 1-2, где параллельное соединение2. Определить ток i1 в заданной схеме, используя теорему об эквивалентном генераторе напряжения.
3. Определить токи во всех ветвях схемы методом узловых потенциалов.
1.2. Методика расчета линейных электрических цепей постоянного тока
1.2 Определяем токи во всех ветвях схемы на основе метода контурных токов. Анализ электрического состояния линейных электрических цепей постоянного тока
Похожие главы из других работ:
1.2 Определение токов во всех ветвях методом контурных токов
1.2 Определение токов схемы методом контурных токов
1.1 Составляем на основании законов Кирхгофа системы уравнений для определения токов во всех ветвях схемы
1.3 Определение токов во всех ветвях схемы на основе метода наложения
2.2 Определение на основе ВАХ токов во всех ветвях схемы и напряжений на отдельных элементах.
3.2 Определение действующих значений токов во всех ветвях электрической цепи
2.2 Расчёт токов в ветвях
1.5 СОСТАВЛЕНИЕ КОНТУРНЫХ УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СЕТИ НА ОСНОВЕ 2-ГО ЗАКОНА КИРХГОФА В МАТРИЧНОЙ ФОРМЕ И В АНАЛИТИЧЕСКОМ ВИДЕ ПРИ ЗАДАНИИ НАГРУЗОК В ТОКАХ
1.4 Экономическое обоснование на основе хозрасчетного метода
1.2 Метод контурных токов
Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы.
3 Расчёт токов методом контурных токов
Определим токи во всех ветвях методом контурных токов
6. Определение токов в ветвях методом контурных токов и составление баланса мощностей
1.2.5 Определение токов КЗ в ветвях генераторов
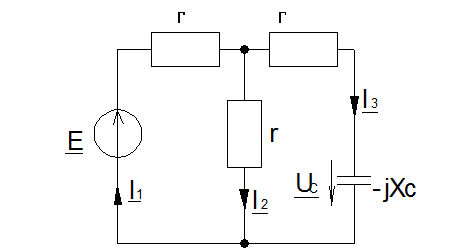
Расчет токов во всех ветвях и напряжения на реактивных элементах электрической цепи
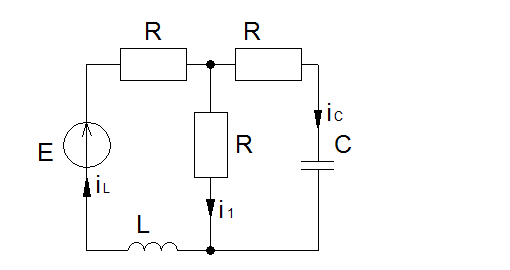
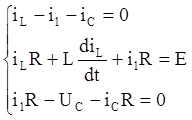 (*) где
(*) где 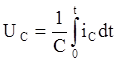

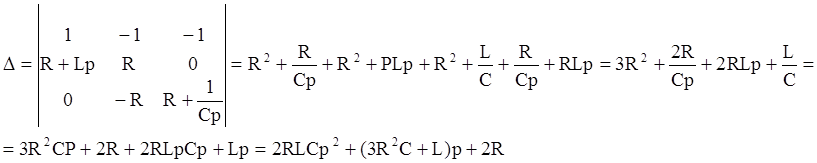
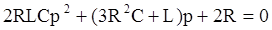
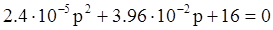
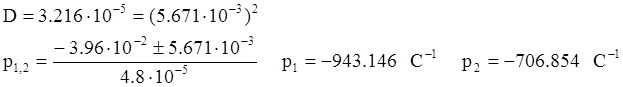
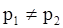 ,
,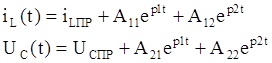 (**)
(**)
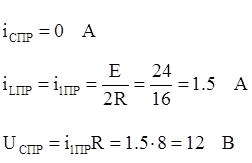
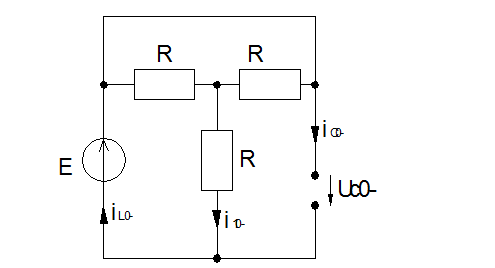
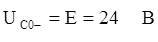
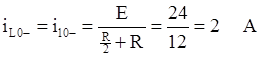
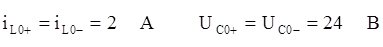
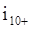 получим исходя из 1-го и 3-го уравнений системы (*):
получим исходя из 1-го и 3-го уравнений системы (*):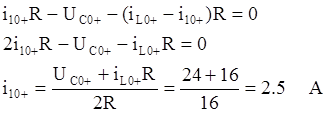
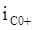 определяется из 1-го уравнения системы (*):
определяется из 1-го уравнения системы (*):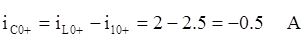
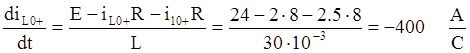
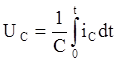 , то
, то 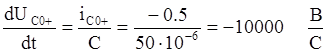
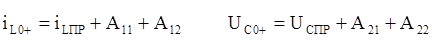
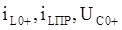 и
и 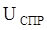 в эти выражения получим:
в эти выражения получим: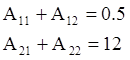

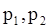 , получим следующие соотношения:
, получим следующие соотношения: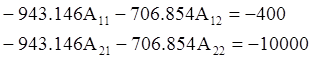
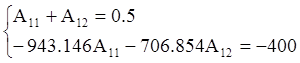
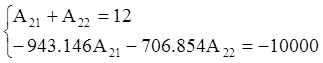
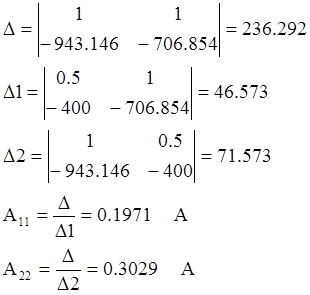
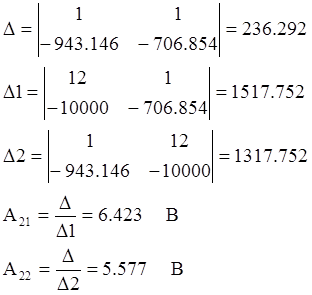
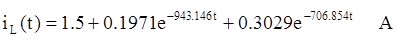
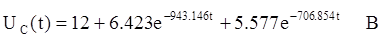
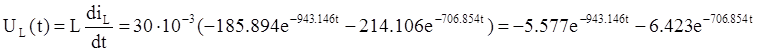 В
В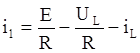
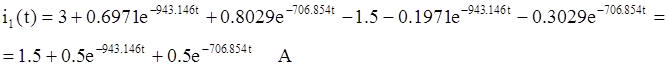
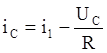
 А
А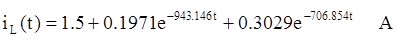
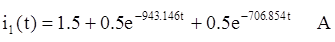
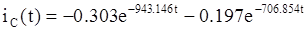 А
А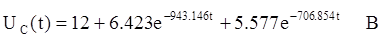
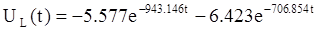 В
В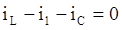
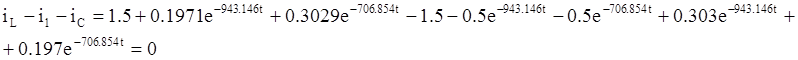
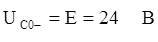
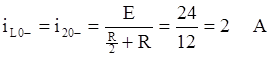
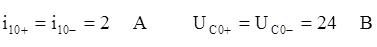
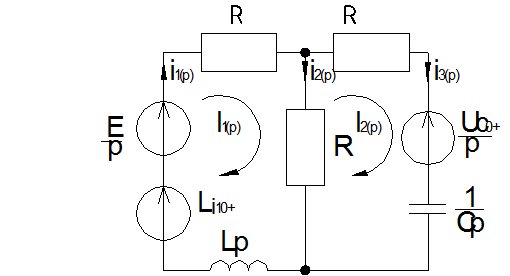
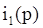 ) применим метод контурных токов.
) применим метод контурных токов.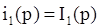
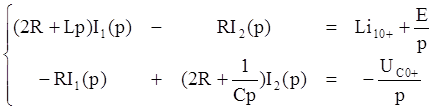
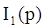 по методу Крамера:
по методу Крамера: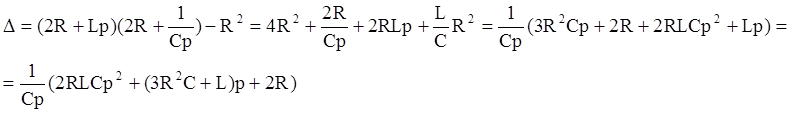
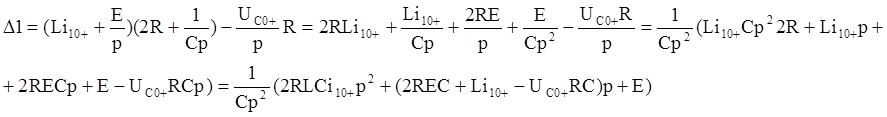
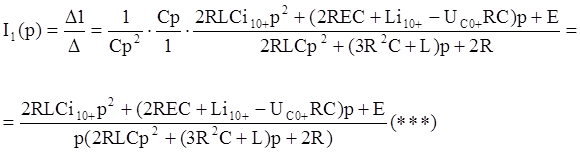
 в
в  , получим следующее выражение:
, получим следующее выражение: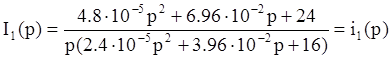
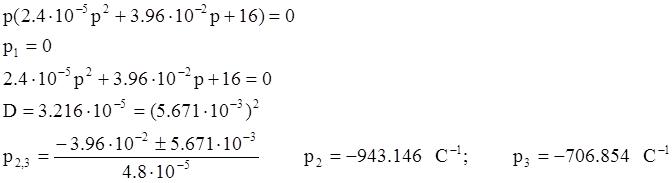
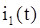 :
: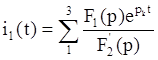
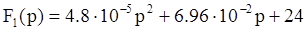 ;
; 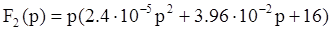
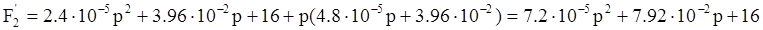
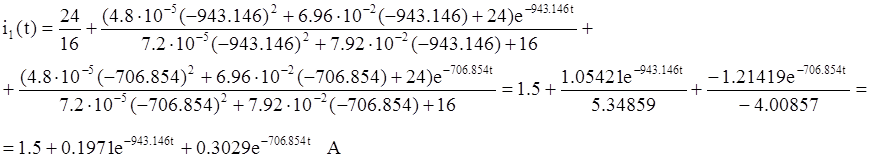
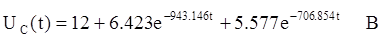
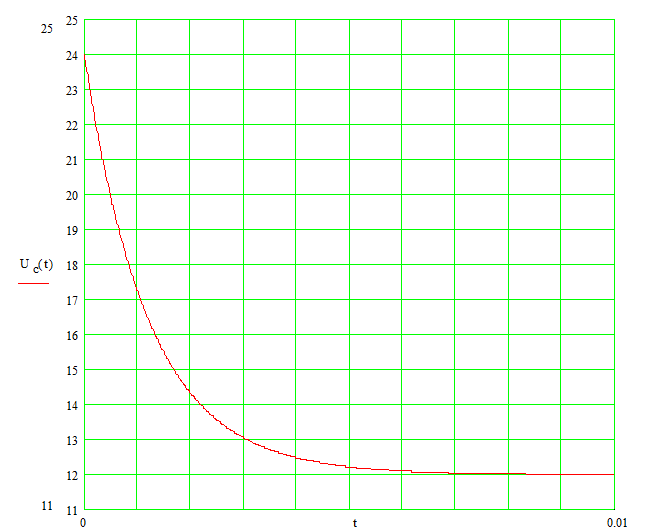
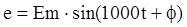
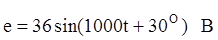
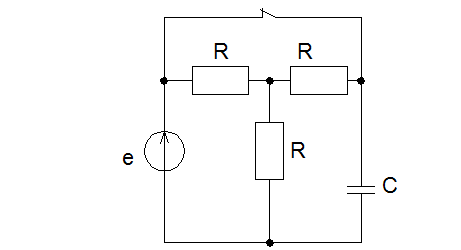
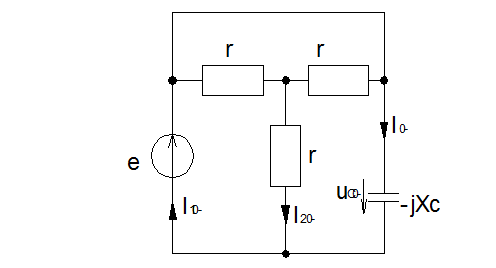
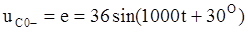
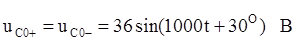
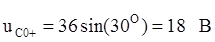
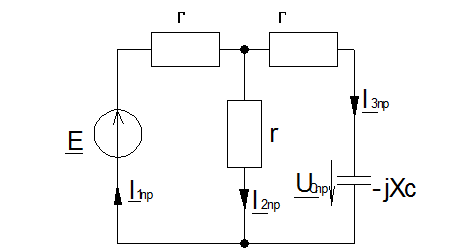
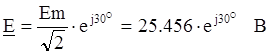
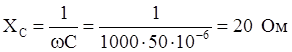
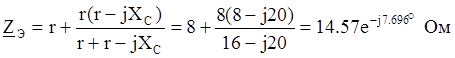
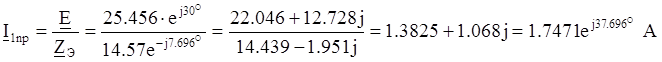
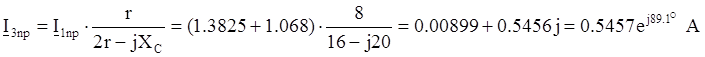
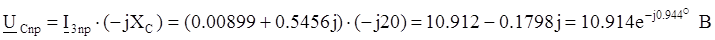
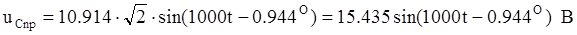
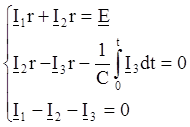
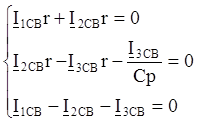
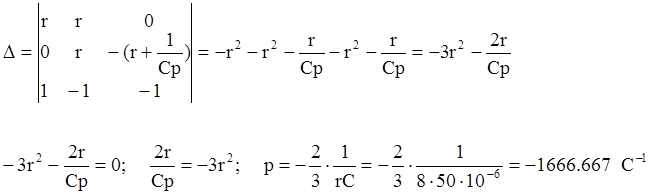
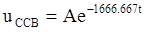 В
В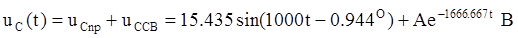
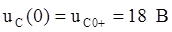 , следовательно:
, следовательно: 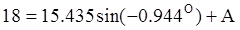
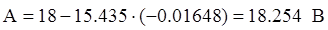
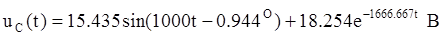
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: