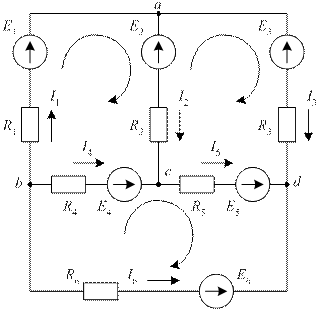
Сложной электрической цепью принято называть разветвленную цепь, содержащую несколько источников, расположенных в разных ветвях. Пример сложной цепи постоянного тока приведен на рис. 22. Рис. 22. Пример сложной цепи постоянного тока Истинные направления токов в ветвях сложной электрической цепи, как правило, неизвестны. Поэтому анализ сложной цепи начинается с выбора так называемых положительных направлений токов в ветвях схемы. На схеме положительные направления токов в ветвях обозначают стрелками с символами тока I. Пример выбора условных положительных направлений токов в ветвях схемы показан на рис. 22. Если в результате анализа цепи получается, что ток в ветви положителен, то истинное направление тока будет совпадать с выбранным положительным направлением тока. Если в результате расчета окажется, что ток в ветви отрицателен, то истинное направление тока противоположно выбранному положительному направлению тока. Т.е. в ходе анализа электрической цепи токи в ветвях рассматриваются как алгебраические величины. Наиболее общий подход к анализу сложных электрических цепей основан на использовании законов Кирхгофа. С помощью законов Кирхгофа составляется система линейных алгебраических уравнений относительно неизвестных токов. Число неизвестных токов равно числу ветвей схемы. Обозначим это число через m. Следовательно, с помощью законов Кирхгофа необходимо составить систему из mуравнений сmнеизвестными токами. При составлении уравнений по законам Кирхгофа необходимо придерживаться следующего правила. Если в схеме nузлов, то с помощью первого закона Кирхгофа составляется (n – 1) независимое уравнение. (Уравнение для последнего узла будет зависимым). Оставшиеся [m–(n–1)] уравнения составляются с помощью второго закона Кирхгофа для так называемых независимых контуров. Независимый контур– это такой контур, при обходе которого появляется хотя бы одна новая ветвь по сравнению с ранее рассмотренными контурами. В разветвленной цепи число независимых контуров всегда меньше общего количества контуров. Поэтому при выборе независимых контуров имеется определенная свобода выбора. Однако число независимых контуров в схеме всегда регламентировано. Схема рис. 22, например, содержит [m – (n – 1)] = [6 – (4 – 1)] = 3 независимых контура. В результате составления (n – 1) уравнения по первому закону Кирхгофа и [m – (n – 1)] уравнения по второму закону Кирхгофа образуется система изm уравнений относительно неизвестных токов ветвей. Решение этой системы позволяет определить токи ветвей. Схема рис. 22 состоит из шести ветвей. Выбранные положительные направления токов в ветвях указаны на схеме стрелками с символами тока I1,I2,I3, I4,I5,I6. Для расчета токов в ветвях этой схемы с помощью законов Кирхгофа необходимо составить систему из шести уравнений. Схема содержит четыре узла (n = 4). По первому закону Кирхгофа необходимо составить три уравнения. Условимся при составлении уравнений по первому закону Кирхгофа токи, выходящие из рассматриваемого узла, брать со знаком «плюс», а входящие в узел, – со знаком «минус». В узел авходит токI1, а выходят токи I2 иI3. Тогда для узлаaуравнение первого закона Кирхгофа будет иметь вид Из узла b выходят токи I1,I4,I6. Уравнение первого закона Кирхгофа для узлаbимеет вид В узел c входят токи I2и I4, а выходит токI5. Поэтому для узлаcможно записать Уравнения первого закона Кирхгофа, составленные для узлов а,b,c, включают в себя токи всех шести ветвей рассматриваемой схемы. Суммируя уравнения, составленные по первому закону Кирхгофа для узлова,b,c, получаем следующее уравнение: Это уравнение отличается от уравнения первого закона Кирхгофа для узла dтолько знаками, а именно: То есть, уравнение первого закона Кирхгофа для узла dзависимое. По второму закону Кирхгофа для рассматриваемой схемы необходимо составить три уравнения для трех независимых контуров. В качестве независимых контуров можно рассматривать, например, левый контур, составленный из первой, второй и четвертой ветвей, правый контур, составленный из второй, третьей и пятой ветвей, и нижний контур, составленный из четвертой, пятой и шестой ветвей. При составлении уравнения второго закона Кирхгофа для каждого независимого контура необходимо придерживаться следующего правила. Если выбранное положительное направление тока в ветви совпадает с направлением обхода контура, то падение напряжения на соответствующем элементе Rв левой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если выбранное положительное направление тока в ветви противоположно направлению обхода контура, то падение напряжения на соответствующем элементеRв левой части уравнения второго закона Кирхгофа берется со знаком «минус». Если направление действия источника ЭДС, указанное на схеме стрелкой, совпадает с направлением обхода контура, то соответствующая ЭДСЕв правой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если направление действия источника ЭДС, указанное на схеме стрелкой, противоположно направлению обхода контура, то соответствующая ЭДСЕв правой части уравнения второго закона Кирхгофа берется со знаком «минус». Направления обхода независимых контуров на схеме рис. 22 выберем по часовой стрелке. Эти направления обхода указаны на схеме стрелками, замыкающимися вдоль каждого из независимых контуров. Рассмотрим поочередно каждый из независимых контуров. В левом контуре токи I1 иI2совпадают с направлением обхода контура. Падения напряжений R1I1,R2I2 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «плюс». Ток I4имеет направление, противоположное направлению обхода левого контура. Падение напряжения R4I4в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «минус». Направление действия источника ЭДС Е1совпадает с направлением обхода контура. В правой части уравнения второго закона Кирхгофа ЭДСЕ1 необходимо взять со знаком «плюс». Направления действия источников ЭДС Е2иЕ4 противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДСЕ2иЕ4 необходимо взять со знаком «минус». Таким образом, для левого независимого контура справедливо следующее уравнение второго закона Кирхгофа: Аналогично для правого и нижнего независимых контуров схемы рис. 22 получаем следующие уравнения второго закона Кирхгофа: При объединении уравнений, составленных по первому и второму законам Кирхгофа для схемы рис. 22, получается следующая система линейных алгебраических уравнений: Решение этой системы позволяет найти токи I1,I2,I3, I4,I5,I6. По известным токам можно найти падения напряжений на элементах схемы, мощности и так далее. Изложенный метод анализа сложных электрических цепей носит название метода законов Кирхгофа. Метод законов Кирхгофа – это наиболее общий подход к анализу электрических цепей. Для анализа сложных электрических цепей могут использоваться и другие методы, например, метод контурных токов, метод узловых потенциалов, метод наложения, метод эквивалентного генератора. Эти методы строятся на основе законов Кирхгофа, закона Ома, принципа наложения. Поэтому они справедливы для линейных цепей. Исключение составляет метод эквивалентного генератора, который предполагает, что ветвь с искомым током может быть и нелинейной. Многообразие методов анализа сложных электрических цепей позволяет в каждом конкретном случае выбрать тот метод, который дает наиболее простой алгоритм расчета. В частности, метод контурных токов и метод узловых потенциалов подобно методу законов Кирхгофа сводятся к решению систем линейных алгебраических уравнений. Однако количество искомых величин, а, следовательно, и порядок систем линейных алгебраических уравнений в этих методах меньше, чем в методе законов Кирхгофа. Для решения систем линейных алгебраических уравнений используются известные математические методы. При малом количестве уравнений в системе можно использовать метод определителей (правило Крамера). При достаточно большом количестве уравнений в системе целесообразно использовать метод последовательного исключения неизвестных Гаусса с выбором главного элемента или итерационные методы решения систем линейных алгебраических уравнений, например, метод Зейделя. Проверку правильности полученного решения можно выполнить путем подстановки найденных значений токов ветвей в систему уравнений, составленную по законам Кирхгофа, или путем составления баланса мощностей (смотри ниже). Рассмотрим поочередно основные методы анализа электрических цепей. Но предварительно рассмотрим общий вопрос, касающийся геометрической структуры электрических цепей. studfiles.net Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными. В любое последовательное соединение может входить произвольное число сопротивлений (резисторов) и источников ЭДС, а также не более одного источника тока. Наличие более одного источника тока в соединении исключается вследствие логического противоречия, т.к. в последовательном соединении через все элементы протекает одинаковый ток и этот ток равен току источника. Если же источников тока несколько, то они должны формировать несколько различных токов, что невозможно по характеру их соединения. Присутствие источника в соединении означает лишь то, что ток в этом соединении задан, поэтому без ущерба для общности выводов источник тока можно вынести за пределы соединения и не рассматривать. Тогда в общем случае в соединение будут входитьm сопротивлений и n источников ЭДС (рис а). Не изменяя режима работы соединения, их можно переместить так, чтобы образовались две группы элементов: сопротивления и источники ЭДС (рис. б). Для этой цепи можно написать уравнение Кирхгофа в виде: U=IR1+IR2+…+IRm+E1+…-En-1+En=I(R1+R2+…Rm)+E1…-En-1+En=IR+E Таким образом, любое последовательное соединение элементов можно представить последовательным соединением одного сопротивленияR и одного источника ЭДС E Причем, общее сопротивление соединения равно сумме всех сопротивлений а общая ЭДС – алгебраической сумме Ток в любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчеты электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Допустим, что в схеме n узлов. Так как любая (одна) точка схемы может быть заземлена без изменения токораспределения в ней, один из узлов схемы можно мысленно зазамлить, т. е.принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n-1. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Кирхгофа. В том случае, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономным, чем метод контурных токов. Первый закон Кирхгофа: Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю I1+I2+I3+…+In=0 Часто встречаются схемы, содержащие всего два узла. Наиболее рациональным методом расчета токов в них является метод двух узлов. Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое ( с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы. Схема имеет два узла. Потенциал точки 2 примем равным нулю φ2 = 0. Составим узловое уравнение для узла 1. φ1(g1+g2+g3)- φ2(g1+g2+g3)=E1g1-E3g3 U12= φ1- φ2= φ1= (E1g1-E3g3)/g1+g2+g3, где g1=1/R1, g2=1/R2, g3=1/R3 – проводимости ветвей В общем виде В знаменателе формулы - сумма проводимостей параллельно включенных ветвей. В числителе - алгебраическая сумма произведений ЭДС источников на проводимости ветвей, в которые эти ЭДС включены. ЭДС в формуле записывается со знаком "плюс", если она направлена к узлу 1, и со знаком "минус", если направлена от узла 1.После вычисления величины потенциала φ1 находим токи в ветвях, используя закон Ома для активной и пассивной ветви. 8.Метод контурных токов При расчете методом контурных токов полагают, что в каждом независимом контуре схмы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей. Т. о., метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было составить для схемы по второму закону Кирхгофа: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.I1R1+I2R2=E1+E2 Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно. Выбираются независимые контуры, и задаются произвольные направления контурных токов.В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид: I11(R1+Ri1)+I11R3-I22R3=E1, I22(Ri2-R2)+I22R3-I11R3=-E2 Перегруппируем слагаемые в уравнениях I11(R1+Ri1+R3)-I22R3=E1=E11, -I11R3+I22(Ri2+R2+R3)=-E2=E22 Суммарное сопротивление данного контура называется собственным сопротивлением контура. Cобственные сопротивления контуров схемы R11=R1+Ri1+R3, R22=Ri2+R2+R3 Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров. R12=R21=R3 где R12 - общее сопротивление между первым и вторым контурами;R21 - общее сопротивление между вторым и первым контурами.E11 = E1 и E22 = E2 - контурные ЭДС.В общем виде уравнения (4.4) и (4.5) записываются следующим образом I11R11+I22R12=E11, I11R21+I22R22=E22 Собственные сопротивления всегда имеют знак "плюс". Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению. Решая уравнения совместно, находим контурные токи I11 и I22 , затем от контурных токов переходим к токам в ветвях. I1=I11, I2=I22,I3=I11-I22. 9.Метод наложения. Данный метод справедлив только для линейных электрических цепей и является особенно эффективным, когда требуется вычислить токи для различных значений ЭДС и токов источников в то время, как сопротивления схемы остаются неизменными. Данный метод основан на принципе наложения (суперпозиции), который формулируется следующим образом: ток в k – й ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности.Аналитически принцип наложения для цепи, содержащей n источников ЭДС и m источников тока, выражается (1) соотношением:Здесь- комплекс входной проводимости k – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях;- комплекс взаимной проводимости k – й и i– й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i– й ветви при равных нулю ЭДС в остальных ветвях.Входные и взаимные проводимости можно определить экспериментально или аналитически, используя их указанную смысловую трактовку, при этом, что непосредственно вытекает из свойства взаимности. Аналогично определяются коэффициенты передачи тока, которые в отличие от проводимостей являются величинами безразмерными. Доказательство принципа наложения можно осуществить на основе метода контурных токов. Если решить систему уравнений, составленных по методу контурных токов, относительно любого контурного тока, например, то получим(2),где -определитель системы уравнений, составленный по методу контурных токов;- алгебраическое дополнение определителя.Каждая из ЭДС в (2) представляет собой алгебраическую сумму ЭДС в ветвях i–го контура. Если теперь все контурные ЭДС в (2) заменить алгебраическими суммами ЭДС в соответствующих ветвях, то после группировки слагаемых получится выражение для контурного тока в виде алгебраической суммы составляющих токов, вызванных каждой из ЭДС ветвей в отдельности. Поскольку систему независимых контуров всегда можно выбрать так, что рассматриваемая h-я ветвь войдет только в один-й контур, т.е. контурный токбудет равен действительному токуh-й ветви, то принцип наложения справедлив для токовлюбых ветвей и, следовательно, справедливость принципа наложения доказана.Таким образом, при определении токов ветвей при помощи метода наложения следует поочередно оставлять в схеме по одному источнику, заменяя остальные их внутренними сопротивлениями, и рассчитать составляющие искомых токов в этих схемах. После этого полученные результаты для соответствующих ветвей суммируются – это и будут искомые токи в ветвях исходной цепи. studfiles.net Метод законов Кирхгофа Сложной электрической цепью принято называть разветвленную цепь, содержащую несколько источников, расположенных в разных ветвях. Пример сложной цепи постоянного тока приведен на рис. 22. Рис. 22. Пример сложной цепи постоянного тока Истинные направления токов в ветвях сложной электрической цепи, как правило, неизвестны. Поэтому анализ сложной цепи начинается с выбора так называемых положительных направлений токов в ветвях схемы. На схеме положительные направления токов в ветвях обозначают стрелками с символами тока I. Пример выбора условных положительных направлений токов в ветвях схемы показан на рис. 22. Если в результате анализа цепи получается, что ток в ветви положителен, то истинное направление тока будет совпадать с выбранным положительным направлением тока. Если в результате расчета окажется, что ток в ветви отрицателен, то истинное направление тока противоположно выбранному положительному направлению тока. Т.е. в ходе анализа электрической цепи токи в ветвях рассматриваются как алгебраические величины. Наиболее общий подход к анализу сложных электрических цепей основан на использовании законов Кирхгофа. С помощью законов Кирхгофа составляется система линейных алгебраических уравнений относительно неизвестных токов. Число неизвестных токов равно числу ветвей схемы. Обозначим это число через m. Следовательно, с помощью законов Кирхгофа необходимо составить систему из m уравнений с m неизвестными токами. При составлении уравнений по законам Кирхгофа необходимо придерживаться следующего правила. Если в схеме n узлов, то с помощью первого закона Кирхгофа составляется (n – 1) независимое уравнение. (Уравнение для последнего узла будет зависимым). Оставшиеся [m–(n –1)] уравнения составляются с помощью второго закона Кирхгофа для так называемых независимых контуров. Независимый контур – это такой контур, при обходе которого появляется хотя бы одна новая ветвь по сравнению с ранее рассмотренными контурами. В разветвленной цепи число независимых контуров всегда меньше общего количества контуров. Поэтому при выборе независимых контуров имеется определенная свобода выбора. Однако число независимых контуров в схеме всегда регламентировано. Схема рис. 22, например, содержит [m – (n – 1)] = [6 – (4 – 1)] = 3 независимых контура. В результате составления (n – 1) уравнения по первому закону Кирхгофа и [m – (n – 1)] уравнения по второму закону Кирхгофа образуется система из m уравнений относительно неизвестных токов ветвей. Решение этой системы позволяет определить токи ветвей. Схема рис. 22 состоит из шести ветвей. Выбранные положительные направления токов в ветвях указаны на схеме стрелками с символами тока I1, I2, I3, I4, I5, I6. Для расчета токов в ветвях этой схемы с помощью законов Кирхгофа необходимо составить систему из шести уравнений. Схема содержит четыре узла (n = 4). По первому закону Кирхгофа необходимо составить три уравнения. Условимся при составлении уравнений по первому закону Кирхгофа токи, выходящие из рассматриваемого узла, брать со знаком «плюс», а входящие в узел, – со знаком «минус». В узел а входит ток I1, а выходят токи I2 и I3. Тогда для узла a уравнение первого закона Кирхгофа будет иметь вид Из узла b выходят токи I1, I4, I6. Уравнение первого закона Кирхгофа для узла b имеет вид В узел c входят токи I2 и I4, а выходит ток I5. Поэтому для узла c можно записать Уравнения первого закона Кирхгофа, составленные для узлов а, b, c, включают в себя токи всех шести ветвей рассматриваемой схемы. Суммируя уравнения, составленные по первому закону Кирхгофа для узлов а, b, c, получаем следующее уравнение: Это уравнение отличается от уравнения первого закона Кирхгофа для узла d только знаками, а именно: То есть, уравнение первого закона Кирхгофа для узла d зависимое. По второму закону Кирхгофа для рассматриваемой схемы необходимо составить три уравнения для трех независимых контуров. В качестве независимых контуров можно рассматривать, например, левый контур, составленный из первой, второй и четвертой ветвей, правый контур, составленный из второй, третьей и пятой ветвей, и нижний контур, составленный из четвертой, пятой и шестой ветвей. При составлении уравнения второго закона Кирхгофа для каждого независимого контура необходимо придерживаться следующего правила. Если выбранное положительное направление тока в ветви совпадает с направлением обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если выбранное положительное направление тока в ветви противоположно направлению обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «минус». Если направление действия источника ЭДС, указанное на схеме стрелкой, совпадает с направлением обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если направление действия источника ЭДС, указанное на схеме стрелкой, противоположно направлению обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «минус». Направления обхода независимых контуров на схеме рис. 22 выберем по часовой стрелке. Эти направления обхода указаны на схеме стрелками, замыкающимися вдоль каждого из независимых контуров. Рассмотрим поочередно каждый из независимых контуров. В левом контуре токи I1 и I2 совпадают с направлением обхода контура. Падения напряжений R1I1, R2I2 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «плюс».Ток I4 имеет направление, противоположное направлению обхода левого контура. Падение напряжения R4I4 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «минус». Направление действия источника ЭДС Е1 совпадает с направлением обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е1 необходимо взять со знаком «плюс». Направления действия источников ЭДС Е2 и Е4 противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е2 и Е4 необходимо взять со знаком «минус». Таким образом, для левого независимого контура справедливо следующее уравнение второго закона Кирхгофа: Аналогично для правого и нижнего независимых контуров схемы рис. 22 получаем следующие уравнения второго закона Кирхгофа: При объединении уравнений, составленных по первому и второму законам Кирхгофа для схемы рис. 22, получается следующая система линейных алгебраических уравнений: Решение этой системы позволяет найти токи I1, I2, I3, I4, I5, I6. По известным токам можно найти падения напряжений на элементах схемы, мощности и так далее. Изложенный метод анализа сложных электрических цепей носит название метода законов Кирхгофа. Метод законов Кирхгофа – это наиболее общий подход к анализу электрических цепей. Для анализа сложных электрических цепей могут использоваться и другие методы, например, метод контурных токов, метод узловых потенциалов, метод наложения, метод эквивалентного генератора. Эти методы строятся на основе законов Кирхгофа, закона Ома, принципа наложения. Поэтому они справедливы для линейных цепей. Исключение составляет метод эквивалентного генератора, который предполагает, что ветвь с искомым током может быть и нелинейной. Многообразие методов анализа сложных электрических цепей позволяет в каждом конкретном случае выбрать тот метод, который дает наиболее простой алгоритм расчета. В частности, метод контурных токов и метод узловых потенциалов подобно методу законов Кирхгофа сводятся к решению систем линейных алгебраических уравнений. Однако количество искомых величин, а, следовательно, и порядок систем линейных алгебраических уравнений в этих методах меньше, чем в методе законов Кирхгофа. Для решения систем линейных алгебраических уравнений используются известные математические методы. При малом количестве уравнений в системе можно использовать метод определителей (правило Крамера). При достаточно большом количестве уравнений в системе целесообразно использовать метод последовательного исключения неизвестных Гаусса с выбором главного элемента или итерационные методы решения систем линейных алгебраических уравнений, например, метод Зейделя. Проверку правильности полученного решения можно выполнить путем подстановки найденных значений токов ветвей в систему уравнений, составленную по законам Кирхгофа, или путем составления баланса мощностей (смотри ниже). Рассмотрим поочередно основные методы анализа электрических цепей. Но предварительно рассмотрим общий вопрос, касающийся геометрической структуры электрических цепей. 1.9. Расчет разветвленной электрической цепи с помощью законов Кирхгофа. Как определяют число независимых контуров в сложной разветвленной схеме
5. Анализ сложных электрических цепей постоянного тока. Метод законов Кирхгофа
5.Метод эквивалентных преобразований
6.Метод узловых потенциалов
7.Метод двух узлов
Анализ сложных электрических цепей постоянного тока.
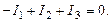

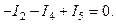
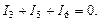
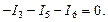
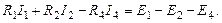
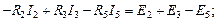
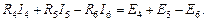
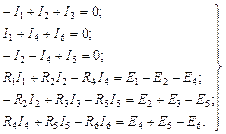
Похожие статьи:
poznayka.org
Второе правило Кирхгофа, теория и примеры
Второе правило Кирхгофа – это один из приемов, который применяют для упрощения расчетов параметров сложных разветвленных цепей постоянного тока. Электрические цепи постоянного тока могут иметь в своем составе большое число сопротивлений, источников тока, множество замкнутых контуров и узлов. Параметры цепи постоянного тока любой сложности можно вычислить, если применять законы Ома и законы сохранения заряда. Правила Кирхгофа являются следствиями вышеназванных законов, с их помощью можно значительно упростить процедуру написания уравнений, связывающих силы тока, сопротивления и электродвижущие силы (ЭДС) для рассматриваемой цепи.
Первое правило Кирхгофа называют правилом узлов. Оно предназначено для написания уравнения для токов, которые сходятся в узле цепи.
Второе правило Кирхгофа относится к замкнутым контурам, которые выделяют в разветвленной цепи. Это правило еще называют правилом контуров.
Формулировка второго правила Кирхгофа
Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) ( ), которые входят в рассматриваемый контур. В виде формулы второй закон Кирхгофа записывают как:
), которые входят в рассматриваемый контур. В виде формулы второй закон Кирхгофа записывают как:
![Rendered by QuickLaTeX.com \[\sum^N_{m=1}{I_mR_m}=\sum^L_{i=1}{\varepsilon_i} \qquad (2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-19a26b422f7240e99dd78f744e6ea01c_l3.png)
Величины 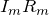 называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.
называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.
Второе правило Кирхгофа — это следствие закона Ома.
Количество независимых уравнений, получаемых при использовании правил Кирхгофа
Применяя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже рассмотренных контуров. Число независимых контуров (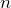 ) равно:
) равно:
![Rendered by QuickLaTeX.com \[n=p-k+1\ \qquad (3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3106528425d5bfcb02c8c54fe3ddf989_l3.png)
где  – число ветвей в цепи;
– число ветвей в цепи;  – количество узлов.
– количество узлов.
Количество независимых уравнений, которые дадут первое и второе правила Кирхгофа равно ( ):
):
![Rendered by QuickLaTeX.com \[s=l+n=k-1+p-k+1=p \qquad (4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-50d5ac61a0a2c9db6ba6e53a9d9e24f8_l3.png)
Вывод: количество независимых уравнений, полученных с использованием обоих правил Кирхгофа равно числу разных токов в рассматриваемой цепи.
Примеры решения задач
ru.solverbook.com
1.9. Расчет разветвленной электрической цепи с помощью законов Кирхгофа
Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.
Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только (– 1) уравнений являются независимыми друг от друга. Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений. Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры. Составим систему уравнений Кирхгофа для электрической цепи (рис. 1.26). Схема содержит четыре узла и шесть ветвей. Поэтому по первому закону Кирхгофа составим уравнения, а по второму, также три уравнения. Произвольно выберем положительные направления токов во всех ветвях (рис. 1.26). Направление обхода контуров выбираем по часовой стрелке. Составляем необходимое число уравнений по первому и второму законам Кирхгофа
;
Рис. 1.26
;;
;.
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
1.10. Метод контурных токов
Расчет любой сложной электрической цепи может быть сведен к решению системы из уравнений, если использовать так называемые контурные токи, т.е. токи, замыкающиеся в независимых контурах. В соответствии с этим методом составляются уравнения только по второму закону Кирхгофа, для чего выбирается необходимое число контуров. При расчете полагают, что в каждом контуре течет свой контурный ток.
Последовательность расчета и вывод основных уравнений проведем применительно к схеме, показанной на рис. 1.26.
Для расчета по методу контурных токов в схеме выделяют независимые контуры. Если в левом верхнем контуре протекает ток, в правом верхнем –, в нижнем –, то при направлении обхода всех контуров по часовой стрелке для контурных токов можно составить следующие уравнения по второму закону Кирхгофа
;
. (1.45)
После преобразования получим:
. (1.46)
Введем обозначения
;;;
;;;
;;,
где – полные или собственные сопротивления первого, второго и третьего контуров;– сопротивления смежных ветвей между первым и вторым, первым и третьим, вторым и третьим контурами, взятые со знаком минус;– контурные ЭДС первого, второго и третьего контуров (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура).
Перепишем уравнения (1.46)
; (1.47)
.
По контурным токам определяют токи в ветвях:
1) токи в наружных ветвях равны контурным токам и совпадают с ними по направлению, если контурный ток является положительным; если контурный ток – отрицательный, то направление тока в ветви меняется;
2) ток в смежной ветви, которая является общей для двух контуров, определяется как алгебраическая сумма соответствующих контурных токов.
Так, для схемы на рис. 1.26 имеем
Порядок расчета методом контурных токов:
1) для каждого независимого контура произвольно выбирают положительное направление контурного тока;
2) для каждого контура составляют уравнение (1.46) по второму закону Кирхгофа. Для этого направление обхода контура выбирают совпадающим с направлением контурного тока;
3) решают систему уравнений относительно контурных токов;
4) определяют токи в ветвях через контурные токи;
проверяют решения по второму закону Кирхгофа.
studfiles.net
Основы матричных методов расчета электрических цепей. (Лекция N 6)
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.

Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где  - источник тока. В соответствии
с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы
можно записать:
- источник тока. В соответствии
с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы
можно записать:
 . . |
(1) |
Однако, для дальнейших выкладок будет удобнее представить ток  как сумму токов k-й
ветви и источника тока, т.е.:
как сумму токов k-й
ветви и источника тока, т.е.:
 . . |
(2) |
Подставив (2) в (1), получим:
 . . |
(3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства

или
 , , |
(4) |
где Z – диагональная квадратная (размерностью n x n) матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
 , , |
(5) |
то
 , , |
(6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров В, записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c=n-m+1. Выражение (6) запишем следующим образом:
 . . |
(7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j–го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j–й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
 , , |
(8) |
где  - столбцовая матрица контурных
токов;
- столбцовая матрица контурных
токов;  - транспонированная контурная
матрица.
- транспонированная контурная
матрица.
С учетом (8) соотношение (7) можно записать, как:
 |
(9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
 , , |
(10) |
 . . |
(11) |
то получим матричную форму записи уравнений, составленных по методу контурных токов:
 , , |
(12) |
где  - матрица контурных сопротивлений;
- матрица контурных сопротивлений;
 - матрица контурных ЭДС.
- матрица контурных ЭДС.
В развернутой форме (12) можно записать, как:
 , , |
(13) |

то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (m=4) и шесть обобщенных ветвей (n=6). Число независимых контуров, равное числу ветвей связи,
c=n-m+1=6-4+1=3.
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.

Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZBT

 .
.
Матрицы ЭДС и токов источников
 |
 |
 |
 |
Тогда матрица контурных ЭДС


 .
.
Матрица контурных токов
 |
 . . |
Таким образом, окончательно получаем:
 ,
,
где  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
 , , |
(14) |
где 
 - диагональная матрица проводимостей
ветвей, все члены которой, за исключением элементов главной диагонали, равны
нулю.
- диагональная матрица проводимостей
ветвей, все члены которой, за исключением элементов главной диагонали, равны
нулю.
Матрицы Z и Y взаимно обратны.
Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
 , , |
(15) |
получим:
 .. .. |
(16) |
Выражение (16) перепишем, как:
 . . |
(17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения на зажимах ветвей:
 . . |
(18) |
Тогда получаем матричное уравнение вида:
 . . |
(19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
 |
(20) |
 , , |
(21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
 |
(22) |
где  - матрица узловых проводимостей;
- матрица узловых проводимостей;
 - матрица узловых токов.
- матрица узловых токов.
В развернутом виде соотношение (22) можно записать, как:
 |
(23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.


Данная схема имеет 3 узла (m=3) и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
Узловая матрица (примем  )
)

Диагональная матрица проводимостей ветвей:
Y
где  .
.
Матрица узловых проводимостей


 .
.
Матрицы токов и ЭДС источников
 |
 |
 |
 |
Следовательно, матрица узловых токов будет иметь вид:


Таким образом, окончательно получаем:
 ,
,
где  ;
;  ;
;  ;
;  ;
;  .
.
Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов расчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
- Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
Ответ:

Ответ:

www.toehelp.ru
Электромонтаж
Результат теста «Методы анализа электрических цепей»
Правильные ответы выделены красным цветом.
1.Физический смысл первого закона Кирхгофа
а) определяет связь между основными электрическими величинами на участках цепи.
б) сумма ЭДС источников питания в любом контуре равна сумме падений напряжения на элементах этого контура.
в) закон баланса токов в узле: сумма токов, сходящихся в узле равна нулю.
г) энергия, выделяемая на сопротивлении при протекании по нему тока, пропорциональна произведению квадрата силы тока и величины сопротивления.
д) мощность, развиваемая источниками электроэнергии, должна быть равна мощности преобразования в цепи электроэнергии в другие виды энергии.
2. Собственное (контурное) сопротивление – это…
а) сумма сопротивлений в каждом из смежных контуров.
б) сумма сопротивлений в каждом независимом контуре.
в) сумма ЭДС в каждом независимом контуре.
г) сумма ЭДС в каждом из смежных контуров.
д) сумма токов, которые протекают в каждом независимом контуре.
3. Ветвь электрической цепи – это…
а) совокупность устройств, предназначенных для получения электрического тока.
б) разность напряжений в начале и в конце линии.
в) ее участок, расположенный между двумя узлами.
г) точка электрической цепи, в которой соединяется три и более проводов.
д) замкнутый путь, проходящий по нескольким ветвям.
4. Количество уравнений, записываемых по методу контурных токов определяется…..
а) числом источников питания в данной схеме.
б) числом ветвей в данной схеме.
в) числом контуров в данной схеме.
г) числом узлов в данной схеме.
д) числом независимых контуров в данной схеме.
5. Достоинство метода контурных токов заключается в том, что…
а) позволяет сократить число уравнений, получаемых по законам Кирхгофа.
б) число независимых узлов меньше числа контуров.
в) позволяет найти токи в ветвях без составления и решения системы уравнений.
г) система уравнений составляется только по второму закону Кирхгофа.
д) в каждом независимом контуре протекает свой ток, который создает падение напряжения на тех сопротивлениях цепи, по которым он протекает.
6. Физический смысл второго закона Кирхгофа
а) определяет связь между основными электрическими величинами на участках цепи.
б) сумма ЭДС источников питания в любом контуре равна сумме падений напряжения на элементах этого контура.
в) закон баланса токов в узле: сумма токов, сходящихся в узле равна нулю
г) энергия, выделяемая на сопротивлении при протекании по нему тока, пропорциональна произведению квадрата силы тока и величины сопротивления.
д) мощность, развиваемая источниками электроэнергии, должна быть равна мощности преобразования в цепи электроэнергии в другие виды энергии.
7. Взаимное сопротивление – это…
а) сумма сопротивлений в каждом из смежных контуров.
б) сумма сопротивлений в каждом независимом контуре.
в) сумма ЭДС в каждом независимом контуре.
г) сумма ЭДС в каждом из смежных контуров.
д) сумма токов, которые протекают в каждом независимом контуре.
8. Электрическая цепь – это…
а) совокупность устройств, предназначенных для получения электрического тока.
б) разность напряжений в начале и в конце линии
в) ее участок, расположенный между двумя узлами
г) точка электрической цепи, в которой соединяется три и более проводов
д) замкнутый путь, проходящий по нескольким ветвям
9. Отличительные признаки простых цепей
а) наличие только одного источника энергии
б) наличие нескольких замкнутых контуров
в) произвольное размещение источников питания
10. Физический смысл закона Ома
а) определяет связь между основными электрическими величинами на участках цепи
б) сумма ЭДС источников питания в любом контуре равна сумме падений напряжения на элементах этого контура
в) закон баланса токов в узле: сумма токов, сходящихся в узле равна нулю
г) энергия, выделяемая на сопротивлении при протекании по нему тока, пропорциональна произведению квадрата силы тока и величины сопротивления
д) мощность, развиваемая источниками электроэнергии, должна быть равна мощности преобразования в цепи электроэнергии в другие виды энергии
11. Контурная ЭДС – это…
а) сумма сопротивлений в каждом из смежных контуров
б) сумма сопротивлений в каждом независимом контуре
в) сумма ЭДС в каждом независимом контуре
г) сумма ЭДС в каждом из смежных контуров
д) сумма токов, которые протекают в каждом независимом контуре
12. Потеря напряжения – это…
а) совокупность устройств, предназначенных для получения электрического тока
б) разность напряжений в начале и в конце линии
в) ее участок, расположенный между двумя узлами
г) точка электрической цепи, в которой соединяется три и более проводов
д) замкнутый путь, проходящий по нескольким ветвям
13. Сущность метода свертки схемы заключается в том, что он…
а) основан на применении законов Кирхгофа
б) основан на эквивалентной замене элементов преобразованного участка
в) основан на возможности эквивалентных преобразований
г) основан на составлении системы уравнений
д) основан на применении закона Ома
14. Физический смысл баланса мощностей
а) определяет связь между основными электрическими величинами на участках цепи
б) сумма ЭДС источников питания в любом контуре равна сумме падений напряжения на элементах этого контура
в) закон баланса токов в узле: сумма токов, сходящихся в узле равна нулю
г) энергия, выделяемая на сопротивлении при протекании по нему тока, пропорциональна произведению квадрата силы тока и величины сопротивления
д) мощность, развиваемая источниками электроэнергии, должна быть равна мощности преобразования в цепи электроэнергии в другие виды энергии
15. Контурный ток – это…
а) сумма сопротивлений в каждом из смежных контуров
б) сумма сопротивлений в каждом независимом контуре
в) сумма ЭДС в каждом независимом контуре
г) сумма ЭДС в каждом из смежных контуров
д) сумма токов, которые протекают в каждом независимом контуре
16. Узел (точка) разветвления – это…
а) совокупность устройств, предназначенных для получения электрического тока
б) разность напряжений в начале и в конце линии
в) ее участок, расположенный между двумя узлами
г) точка электрической цепи, в которой соединяется три и более проводов
д) замкнутый путь, проходящий по нескольким ветвям
17. Главное условие эквивалентного преобразования схем:
а) составление и решение системы уравнений, получаемых по первому закону Кирхгофа
б) преобразование схемы, при котором токи и напряжения в непреобразованной части остаются неизменными
в) составление и решение системы уравнений, получаемых по второму закону Кирхгофа
г) преобразование схемы в соответствии с законами Кирхгофа
д) преобразование схемы, при котором токи и напряжения в непреобразованной части изменяются
18. Контур электрической цепи – это…
а) совокупность устройств, предназначенных для получения электрического тока
б) разность напряжений в начале и в конце линии
в) ее участок, расположенный между двумя узлами
г) точка электрической цепи, в которой соединяется три и более проводов
д) замкнутый путь, проходящий по нескольким ветвям
19. Собственное (контурное) сопротивление – это…
а) сумма сопротивлений в каждом из смежных контуров
б) сумма сопротивлений в каждом независимом контуре
в) сумма ЭДС в каждом независимом контуре
г) сумма ЭДС в каждом из смежных контуров
д) сумма токов, которые протекают в каждом независимом контуре
www.electromontag-pro.ru







Поделиться с друзьями: