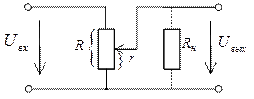
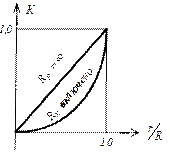
Последовательное соединение резисторов Iобщ = I1 = I2 = I3 Uобщ = U1 + U2 + U3 Параллельное соединение резисторов Iобщ = I1 + I2 + I3 Uобщ = U1 = U2 = U3 Реостат – это переменный резистор, который включается в цепь последовательно с потребителем нагрузки. Изменяя положение ползунка, в цепи меняется ток от 0 до max. Реостат применяется для изменения тока в цепи. В электрических схемах встречается понятие – реостатное включение нагрузки. Реостатное включение нагрузки Uист Rр + Rн RP = 0 Uист Rр + Rн В радиосхемах возникает необходимость подавать на потребитель напряжение меньше чем развивает источник, тогда между источником и нагрузкой включается гасящий резистор. Применение – в схеме создания напряжения смещения на участке эмиттер-база транзистора. Гасящий резистор Uгас = Uист – URн PRгас = I2 – Rгас Делитель напряжения Делитель напряжения – это цепь, состоящая из нескольких последовательно соединённых резисторов обеспечивающих подачу на потребитель некоторой части напряжения источника. Потенциометр – это переменный резистор, с части которого снимается напряжения источника. Потенциометр Применение – регулировка громкости на входе усилителя низкой частоты. selectelement.ru Рисунок 1 - Исходная схема Допустим необходимо найти сопротивление схемы относительно точек A и B. Заданы сопротивления резисторов: R1=20, R2=20, R3=10, R4=20, R5=8, R6=4, R7=4. Преобразуем треугольник сопротивлений R1, R2, R3 в звезду сопротивлений R12, R23, R13: Рисунок 2 - Схема с преобразованным в звезду треугольником Сопротивления R12, R13, R23 найдены по формулам 1-3: Чтобы найти сопротивление луча звезды надо произведение сопротивлений прилегающих к нему сторон треугольника разделить на сумму сопротивлений всех сторон треугольника. Преобразуем последовательное соединение резисторов R13 и R6 в резистор R136 и аналогично преобразуем последовательное соединение резисторов R23 и R7 в резистор R237: Рисунок 3 - Схема3 Сопротивления резисторов R136 и R237 найдены по формулам 4 и 5: Преобразуем параллельное соединение резисторов R136 и R237 в резистор R136IIR237: Рисунок 4 - Схема4 Найдем R136IIR237 по формуле 6: Далее преобразуем схему 4 к виду: Рисунок 5 - Схема5 Найдем сопротивление которое стоит справа: Теперь, заменой параллельного соединения резисторов, в схеме на рисунке 5, одним резистором Rэ, находится эквивалентное сопротивление всей схемы: Найдем Rэ: electe.blogspot.com Это такое соединение, при котором все элементы идут один за одним без разветвлений. Свойства последовательного соединения 1. Ток во всех резисторах одинаков- I1 = I2 = I3; 2. Общее напряжение цепи равно сумме напряжений на всех резисторах- U=U1 + U2 + U3; 3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков - Rвх= R1 + R2 + R3; 4. Чем больше сопротивление участка, тем больше на нём падает напряжение- ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение. Свойства параллельного соединения резистора: 1. Общее напряжение цепи равно напряжению на каждом участке- U = U1 = U2 = U3 2. Общий ток цепи равен сумме токов на всех участках- I = I1 + I2 + I3 3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению Общая проводимость цепи равна сумме проводимостей на каждом участке. G = G1 + G2 + G3 4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем. При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать 1. 2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений Тестовые задания: Смешанное соединение резисторов Пример решения задач Дано: U = 60 В R1 = 7 Ом R2 = 12 Ом R3 = 4 Ом Найти: I1; I2; I3 = ? Rвх = R1 + R2 - 3 Rвх =R1+R2∙3= 7 + 3 = 10 Ом I1 = Iвх = 6 А U2 - 3 = I∙R2 - 3 - находим напряжение разветвленного участка: U2 - 3 = I∙R2 - 3 = 6∙3 = 18 В U2 - 3 = U2 = U3 =18 В- т.к. параллельное соединение Дано: U=240 В R1 = 20 Ом R2 = 120 Ом R3 = 40 Ом R4 = 60 Ом R5 = 30 Ом R6 = 20 Ом Найти: I1-6 -? Rвх=R1+R2-3+R4-6 = 20 + 30 +10 = 60 Ом; U2-3 =I∙R2-3= 4∙30 = 120 В; U2 - 3 = U2 = U3; U4-6=I∙R4-6=4∙10=40B; U4-6=U4=U5=U6; Дано: E = 20 В Ri=2Ом R1 = 9Ом R2 = 6 Ом R3 = 12 Ом R4 = 1 Ом R5 = 2 Ом R6 = 1 Ом R4-6 = R4 + R5 + R6; R3-6 = 3 Ом; Rвх = R1 + R3-6 +R2 = 9 + 3 + 6 = 18 Ом; I= I=I1=I2=1А; U3-6=U3=U4-6; I3= I4=I5=I6= Cоставим подробное уравнение баланса мощностей для данной схемы. Оно является проверкой правильности решения задачи. Pu=Pн+Р0; EI=I21∙R1+ I22∙R2+ I23R3+I42R4+I25R5+I26+I2Ri; 20∙1=12∙9+12∙6+(0,25)2∙12+(0,75)2∙1+(0,75)22+(0,75)21+12∙2; 20Вт=20Вт- задача решена верно ДЕЛИТЕЛИ НАПРЯЖЕНИЯ Делитель напряжения- это четырёхполюсник, у которого коэффициент передачи меньше единицы. Рассмотрим Г-образный делитель напряжения: Чтобы рассчитать коэффициент передачи надо: 1) задать произвольное напряжение на входе; 2) любым способом рассчитать напряжение на выходе; 3) взять их отношения: Для Г-образного делителя напряжения коэффициент передачи равен отношению выходного сопротивления ко входному. б) Делитель напряжения с плавной регулировкой (потенциометр) В нижнем положении движка К = 0. В верхнем положении движка К = 1 Так как в нижнем положении движка Uвыхснимаетсяс провода, а в верхнем положении Uвых = Uвх 1) Если нагрузка не подключена делитель работает в режиме холостого хода и зависимость коэффициент передачи от положения движка потенциометра будет линейной. 2) Если подключить нагрузку, то характеристика будет другой: получается параллельное соединение Rн и r и при том же положении движка напряжение участка уменьшается. В крайних точках коэффициент передачи остаётся тем же, поэтому характеристика становиться нелинейной. Вывод: чтобы при подключении нагрузки характеристика приближалась к линейной нагрузку нужно брать высокоомную. Тестовые задания: ПРЕОБРАЗОВАНИЕ ТРЕУГОЛЬНИКА В ЭКВИВАЛЕНТНУЮ ЗВЕЗДУ ( В некоторых схемах, например, в мостовых, возникает необходимость преобразовать треугольник сопротивления в эквивалентную звезду. При таком преобразовании напряжение между узлами не должны изменяться и токи в неизменной части схемы не должны изменяться. Сопротивления луча эквивалентной звезды равняется произведению сопротивлений сторон треугольника, примыкающих к той же вершине, что и луч звезды, делённому на сумму сопротивлений всех сторон треугольника. Рассмотрим этот метод на конкретной мостовой схеме. Заменим Пример решения задачи Дано: U = 56 В R1=R2=40Ом R3 = 35 Ом R4 = 10 Ом R5 = 50 Ом Найти: I1-5=? 1) Изобразим преобразованную схему и рассчитаем ее. UОД = I∙RОД = 2∙24 = 48 В 2) Направляем токи в первоначальной схеме от плюса источника к минусу, в R5 ток направляем произвольно; 3) Составляем уравнения по второму закону Кирхгофа, для треугольника, который не заменяем. I2∙R2 - I3∙R3 = - I5∙R5 0,3∙40-1,2∙35 = -I5∙50 32 - 84 = -I5∙50 I5 = 0,2A 3) Чтобы найти I1 и I4 составляем уравнения по первому закону Кирхгофа для узлов В, С. I1 + I5 - I2 = 0 (B) I1 = I2 - I5 I1 = 0,8 - 0,2 = 0,6A I5 + I3 + I4 = 0 (C) I4 = I3 + I5 I4 = 1,2 + 0,2 = 1,4A Пример решения задачи Дано: U =200 R1 = 10 Ом R2 = 70 Ом R3 = 20 Ом R4 = 130 Ом R5 = 30 Ом R6 = 10 Ом Найти: I1-6, - ? R4B = RB + R4 = 2 + 130 = 132 Ом RC5 = RC + R5 = 14 + 30 = 44 Ом Rвх = 33 + 10 + 7 = 50 Ом I=I6=4A UОД = I∙RОД = 4∙33 = 132 В 0 = -I3∙R3 + I4∙R4 - I5∙R5 I3∙R3 = I4∙R4 - I5∙R5 I3∙20 = - 1∙130-3∙30 I3∙20 = 40 I3 = 2A (В) I1 - I3 - I4 = 0 I1 = I4 + I5 = 1 + 2 = 3A (C) I2 + I3 - I5 = 0 I2 = I5 - I3 = 3 - 2 = 1A Читайте также: lektsia.com Рассмотрим различные соединения электрических сопротивлений (резисторы, электронагревательные элементы, электролампы, электромоторы и т.д.). Места объединения соединительных (подводящих) металлических проводников от различных электрических сопротивлений называют узлами соединения. Наиболее простыми соединениями электрических сопротивлений являются последовательное и параллельное. В дальнейшем различные соединения электрических сопротивлений будем рассматривать на примере резисторов. П. 1. При последовательном соединении резисторов в каждом узле объединяются соединительные проводники только от двух разных резисторов (рис. 1). В электрических Схемах прямоугольники используются просто как символы резисторов, поэтому размеры прямоугольников не имеют принципиального значения. Все резисторы в электрических схемах будем обозначать прямоугольниками приблизительно одинаковых размеров, а обозначения и значения сопротивлений резисторов будем ставить внутри прямоугольников или около них. Основные (независимые) законы для участка электрической цепи постоянного тока, состоящего из последовательно соединенных резисторов (см. рис. 1), имеют вид: или кратко: Соотношения (1, a) следуют из определения постоянного (стационарного) электрического тока для неразветвленного участка электрической цепи. При учете закона Ома для однородного участка электрической цепи из формул (1, a), (1, b) дополнительно получаем: Формула (1, d) непосредственно следует из формулы для электрического сопротивления однородных проводников (резисторов), находящихся в тепловом равновесии с окружающей средой: Преобразуем выражения для сопротивлений однородных проводников (ρi, li , Si), введя понятие эталонного вещества (ρэт), за которое можно принять любое вещество по желанию, и эталонной площади поперечного сечения проводников (Sэт). Тогда где Заменим набор резисторов Ri (ρi, Si, li) набором такого же числа резисторов с теми же по величине электрическими сопротивлениями, но изготовленными из одного и того же вещества (ρэт) с одинаковыми площадями поперечных сечений (Sэт). Последовательное соединение проводников при такой замене означает объединение частей (кусков) одного и того же однородного проводника в единый однородный проводник, поэтому После домножения обеих частей этого равенства на (ρэт/Sэт) получаем: или кратко При учете (3, b) Riэт.=Ri и поэтому что обобщает (1, d) на случай любого числа последовательно соединенных резисторов. Если в каком-то узле электрической схемы объединены соединительные проводники более чем от двух резисторов, то никакая пара этих резисторов не соединена между собой последовательно. П. 2. При параллельном соединении резисторов соединительные проводники от одних концов резисторов объединяются в одном узле, а соединительные проводники от противоположных концов этих резисторов — в другом общем для них узле (рис. 2). Основные (независимые) законы для участка электрической цепи, состоящего из параллельно соединенных резисторов, имеют следующий вид: Формула (5, а) является следствием определения электрического напряжения на участке цепи и определения параллельного соединения проводников. Формула (5, b) непосредственно следует из определения постоянного (стационарного) электрического тока для разветвленного участка цепи. Часто закон (5, b) называют 1-ым законом (правилом) Кирхгофа для разветвленной электрической цепи. Из формул (5, а), (5, b) при учете закона Ома для однородного участка электрической цепи дополнительно получаем: Перепишем формулу (5, d) для случая двух параллельно соединенных резисторов следующим образом: В случае трех параллельно соединенных резисторов Итак, общее сопротивление параллельного соединения резисторов меньше сопротивления любого из резисторов, входящего в параллельное соединение. Обобщим формулу (5, d) на любое число N параллельно соединенных между собой резисторов и выделим из нее частный случай, когда электрические сопротивления всех резисторов одинаковы; тогда Таким образом, общее сопротивление параллельного соединения одинаковых резисторов меньше сопротивления одного резистора из этого соединения во столько раз, сколько одинаковых резисторов содержится в параллельном соединении. Формулы (5, е) и (5, d) можно получить, не используя закон Ома для однородного участка электрической цепи постоянного тока, а исходя только из формулы (2) для сопротивления однородных проводников. Параллельное соединение N одинаковых проводников эквивалентно одному проводнику той же длины с площадью поперечного сечения S0=N*S, поэтому что совпадает с (5, е). Доказательство обобщенной формулы (5, d) для любого числа N параллельно соединенных различных резисторов выполним в два этапа. Сначала заменим резисторы из разных веществ (рi) и в общем случае с различными li и Si на эквивалентные по величине электрического сопротивления резисторы одинаковой длины (lэт), изготовленные из одного и того же вещества (ρэт)- Очевидно, что где Параллельное соединение проводников одинаковой длины (i3T), изготовленных из одного и того же вещества (рэт)> дает однородный проводник той же длины (i3T) из того же вещества (рэт) с площадью поперечного сечения Из (6, а, b, с) получаем: что подтверждает все вышеприведенные формулы и качественные выводы для параллельного соединения резисторов. П. 3. Сопротивления любых соединительных проводников в электрических схемах, если это не оговорено специально, считаются ничтожно малыми по сравнению с сопротивлениями резисторов и в расчетах не учитываются; поэтому их можно не только укорачивать, но при необходимости и удлинять при преобразованиях схем соединений резисторов. В электрических схемах соединительные проводники условно изображают тонкими проводниками (линиями). На самом же деле в соответствии с формулой (2) площадь поперечного сечения соединительных проводников должна быть достаточно большой, что достигается параллельным соединением тонких проводников с диэлектрическим покрытием (многожильные проводники), изготовленных из недорогих веществ с минимальными удельными сопротивлениями (алюминий, медь [1]). Резисторы, наоборот, изготавливают из веществ с максимально большими удельными сопротивлениями (фехраль, нихром, реотан, константан, мангалин, никелин, сталь, железо [1]) в виде тонких спиралей, заключенных в диэлектрические твердые оболочки. П. 4. Параллельное соединение трех резисторов (см. рис. 2) можно осуществить и по-другому, как показано на рисунке 3. Проиллюстрируем эквивалентность электрических схем, изображенных на рисунках 2, 3. В схеме, изображенной на рисунке 3, оставим участок ВС с резистором R2 без изменения и начнем укорачивать соединительные проводники А'С и D'B от узлов А' и D'. В пределе при А'С → 0 ← D'B схема, изображенная на рисунке 3, переходит в схему, изображенную на рисунке 2. Общий метод эквивалентного преобразования сложных электрических схем, основанный на понятии потенциала постоянных электрический полей, будет рассмотрен в отдельной статье. В развитие темы преобразования электрических схем предлагаю читателям подумать над следующими заданиями. Задание 1. Изобразите более наглядно приведенные соединения четырех резисторов: Задание 2. Расшифруйте приведенное соединение пяти резисторов. П. 5. Рассмотрим схему соединения резисторов, приведенную ниже на рисунке 4, о. Анализ любой электрической схемы начинают с разметки узлов соединения резисторов и при необходимости их обозначения. Сразу же отметим, что никакая пара резисторов R1, R2, R6 (R4, R5, R6) не соединена между собой ни последовательно, ни параллельно; так как в узле В (Е) объединены соединительные проводники от одних концов трех резисторов R1, R2, R6 (R4, R5, R6 ), а соединительные проводники от противоположных концов этих резисторов не объединены в один общий для них узел. Техническое название соединения трех резисторов R1, R2, R6 (R4, R5, R6 ) будет дано ниже. План эквивалентного преобразования соединения резисторов, изображенного на рисунке 4, Ъ, очевиден и, в большой степени, благодаря проведенной разметке узлов соединения резисторов. На первой стадии обучения целесообразно проводить преобразования соединений резисторов поэтапно, рассматривая последовательность все более простых электрических схем после каждой замены нескольких резисторов одним эквивалентным резистором. В рассматриваемом случае легко сразу наглядно показать виды соединений всех резисторов в схеме на рисунке 4, b. Для этого надо участок АВ повернуть по ходу часовой стрелки, а участок FE — против хода часовой стрелки на 90°. Полученное таким образом соединение резисторов эквивалентно соединению, указанному на рисунке 4, с. Вычисление общего сопротивления по схеме 4, с элементарно и дает следующие результаты: Задание 3. Сопоставьте с электрической схемой, изображенной на рисунке 4, а, антисхему (схему-антипод), заменяя в исходной схеме последовательные соединения резисторов на параллельные и, наоборот, параллельные — на последовательные. П. 6. К числу наипростейших соединений резисторов, кроме последовательного и параллельного, относятся соединения резисторов по схемам "треугольник" (рис. 5, а) и "звезда" (рис. 5, b). Кстати, в соединениях 4 b, с резисторы R1, R2, R6 (R4, R5, R6 ) соединены между собой по схеме "звезда". Сформулируем условия эквивалентности (по величине электрического сопротивления) соединений резисторов по схемам "треугольник" и "звезда", приняв за основу статьи [3]. В общем случае (рис. 6) условия эквивалентности состоят из трех уравнений: Рассмотрим частный случай, когда сопротивления всех резисторов в "треугольнике" одинаковы и равны R. Как следствие этого, сопротивления всех резисторов в эквивалентной "звезде" также будут одинаковыми и равными r. В этом частном случае все три условия (7) совпадают между собой. При подключении источника постоянного элекрического напряжения между любыми двумя клеммами (полюсами) "треугольника" по всем его резисторам протекает постоянный электрический ток и все его резисторы дают отличный от нуля вклад в общее сопротивление участка цепи. При подключении источника постоянного электрического напряжения к любым двум клеммам (полюсам) "звезды" постоянный электрический ток в ней протекает только по двум резисторам, третий всегда лишний — тупиковый; но каждый раз разный. Из условия ROAB=rOAB рассматриваемом частном случае получаем: (2/3)R=2r. Итак, Простейшее соединение резисторов, не содержащее последовательно и параллельно соединенных резисторов, называют "мостиком" (рис. 7). Замена любого "треугольника" в "мостике" на эквивалентную "звезду" или наоборот позволяет довести вычисление общего сопротивления "мостика" до конца по законам последовательного и параллельного соединений резисторов. Расчетная целесообразность замен "треугольников" на "звезды" и наоборот ограничивается, кроме случая R1=R2=R3=R(r1=r2=r3=r), случаем, когда среди трех резисторов "треугольника" или "звезды" имеются два одинаковых резистора. В общем случае, когда сопротивления всех резисторов в "треугольнике" и "звезде" различны, решение задачи об эквивалентности этих соединений резисторов является очень сложным. Поэтому надо изучать и другие методы эквивалентного преобразования сложных соединений резисторов. Если среди сопротивлений "мостика" (см. рис. 7) имеются пропорциональные сопротивления (a) R1/R3-R2/R4, b) R1/R2=R3/R4), то появляются оси симметрии распределения сопротивлений в "мостике", и при подключении "мостика" к источнику постоянного электрического напряжения ток по резистору R5 не протекает. Поэтому резистор R5 можно удалить из схемы, не изменяя ее общего электрического сопротивления, а узлы, между которыми он был включен в "мостике", при желании можно объединить в один узел. Задание 4. Вычислите общее сопротивление соединения одинаковых резисторов (R) по схеме пятиконечной звезды (рис. 8) между полюсами: а) А и В; b) В и В'; с) А и С; d) А и D; е) D и D'; f) А и Е; g) А и F. П. 7. Рассмотрим роль измерительных приборов в макроскопической физике, где нет принципиального различия между объектами и приборами. И те, и другие состоят из огромного количества молекул, исчисляемого молями вещества, т. е. N=v*NA=(m/M)*NA где NA=6,02*1023 моль-1 — постоянная Авогадро. Не рассматривая устройство и принципы работы измерительных приборов, отметим, что все они имеют шкалу с определенной ценой деления и соответствующим интервалом значений измеряемой величины. В электрических цепях величину тока и напряжения измеряют соответственно амперметрами и вольтметрами. Электрические измерительные приборы дополнительно характеризуются их внутренними электрическими сопротивлениями. Как любое электрическое сопротивление, амперметры и вольтметры, независимо от их специфики, можно подключать к другим сопротивлениям (резисторы, электронагревательные элементы, электролампочки, электромоторы и т.д.) как последовательно, так и параллельно. Амперметр показывает величину тока, протекающего через него, и все сопротивления, последовательно соединенные с ним; а вольтметр — электрическое напряжение на внутреннем сопротивлении вольтметра и всех сопротивлениях, параллельно соединенных с ним. Подключение измерительных приборов в электрическую цепь изменяет сопротивления участков цепи и всей цепи в целом, что приводит к изменению распределений токов и напряжений в электрической цепи. Изменение состояния системы в результате проведения измерений и зависимость результатов измерений от измерительных приборов обычно обсуждается на уровне микросистем (отдельных микрообъектов) в квантовой механике в вузовских курсах физики. Однако эта зависимость существует и на макроуровне, но ее либо не замечают, либо не обращают на нее должного внимания. Во избежание рассмотрения выше описанной сложной проблемы на начальной стадии изучения электрических цепей договариваются использовать идеальные измерительные приборы. Идеальный амперметр — это амперметр, внутреннее сопротивление которого много меньше всех сопротивлений, содержащихся в электрической цепи. В расчетах внутреннее сопротивление идеального амперметра не учитывается (гА=0). Поэтому идеальные амперметры нельзя включать параллельно с другими сопротивлениями, так как электрический ток, подходящий к параллельному соединению, содержащему идеальный амперметр, полностью пойдет через идеальный амперметр, выключив из электрической цепи сопротивление(я), к которому^™) он подключен параллельно. Идеальные амперметры включаются только последовательно с сопротивлениями и не искажают распределений токов и напряжений в электрических цепях. Идеальный вольтметр — это вольтметр, внутреннее сопротивление которого много больше всех сопротивлений, содержащихся в электрической цепи. В расчетах внутреннее сопротивление идеального вольтметра полагается равным бесконечности. Поэтому идеальные вольтметры нельзя включать последовательно с сопротивлениями, ибо тогда по этим участкам цепи не будет протекать электрический ток. Идеальные вольтметры подключаются к сопротивлениям только параллельно и не искажают распределения токов и напряжений в электрических цепях. Если в условии задачи приведена электрическая схема с идеальными амперметрами и вольтметрами и заданы показания этих приборов, то надо идеальные приборы удалить из схемы, образно говоря, как паутину, а показания приборов "перенести" на другие сопротивления электрической цепи с учетом их соединения с измерительными приборами. Использование понятий об идеальных амперметрах и вольтметрах полезно до поры до времени, но когда-то надо обязательно перейти к реальным измерительным приборам и учитывать в расчетах конечные значения их внутренних сопротивлений со всеми вытекающими отсюда усложнениями [3]. При использовании реальных измерительных приборов возникают вопросы о точности измерений величин токов и напряжений на участках электрической цепи, а также проблема увеличения цены деления шкалы приборов. При уменьшении внутреннего сопротивления амперметра, подключаемого последовательно к сопротивлениям электрической цепи, его показания возрастают и стремятся к истинному значению величины электрического тока, протекающего через заданные сопротивления электрической цепи до подключения амперметра в электрическую цепь. При увеличении внутреннего сопротивления вольтметра, подключенного параллельно к сопротивлениям электрической цепи, его показания возрастают и стремятся к истинному значению электрического напряжения на данных сопротивлениях до подключения вольтметра в электрическую цепь. Для расширения интервала значений измеряемых токов и соответствующего увеличения цены деления шкалы амперметра к нему параллельно подключают проводник (шунт), сопротивление которого меньше внутреннего сопротивления амперметра. Для увеличения цены деления шкалы амперметра в п раз к нему надо параллельно подсоединить шунт с сопротивлением rш=rа/(п-1). Для увеличения цены деления шкалы вольтметра в п раз к нему надо последовательно подсоединить проводник (дополнительное сопротивление) с Rдоп=(n-1)RB. Рекомендую решить задачи № 527, 534, 553 — 557 из [2] на использование реальных измерительных приборов в цепях постоянного электрического тока. Ответы к заданиям, приведенным в статье Задание 1 Все соединения резисторов в этом задании содержат соединение, изображенное на рисунке 3. Ввиду эквивалентности соединений, изображенных на рисунках 2, 3, имеем: Задание 2 Выделим в заданном соединении резисторов соединение, изображенное на рисунке 3. При учете эквивалентности соединений, изображенных на рисунках 2, 3, получаем: Заменяя параллельное соединение резисторов R1, R2, R3, одним резистором RI получаем новое соединение резисторов R5, R4, RI типа 2—3. Задание 3 Задание 4 Заменяя поэтапно последовательные (параллельные) соединения резисторов одним эквивалентным резистором, уменьшаем число резисторов в электрической схеме и сводим рассматриваемую схему либо сразу к одному резистору, либо к соединению, содержащему только "треугольники" и "звезды". Во втором случае соединение резисторов по схеме "треугольник" заменяем эквивалентным соединением резисторов по схеме "звезда" и доводим преобразование соединения резисторов до одного эквивалентного резистора. При реализации вышеизложенной программы получаем: a) RAB=(19/30)*R; b) RBB',=(8/15)*R; с) RAC=(6/5)*R; d) RAD=(31/30)*R; e) RDD'=(4/5)*R; f) RAE=(22/15)*R; g) RAF=(7/6)*R. Альтернативный метод вычисления сопротивлений электрических схем на основе учета симметрии схем и распределения потенциала постоянного электрического поля в них будет рассмотрен в отдельной статье. Литература 1. Кошкин, Н. И. Справочник по элементарной физике / Н. И. Кошкин, М. Г. Ширкевич. — М. : Наука, 1965. 2. Балаш, Б. А. Задачи по физике и методы их решения / Б. А. Балаш. — М. : Просвещение, 1967. 3. Петрович, Г. И. Цепи постоянного электрического тока / Г. И. Петрович, Э. М. Шпилевский // Репетитор. — 1996. — № 5(8). — С. 43—48; 1997. — № 6(9). — С. 42—47; 1997. — № 1(10). — С. 41—47. www.alsak.ru В радиосхемах применяются последовательное, параллельное и комбинированное соединения резисторов. Эквивалентное сопротивление последовательно соединенных резисторов равно сумме величин сопротивлений этих резисторов: Rэ = R1 + R2 + ... + Rn Например, если последовательно соединены два резистора с номинальными сопротивлениями 100 Ом и 1 кОм, то номинальное сопротивление эквивалентного резистора составит 1,1 кОм [(100 + 1000) Ом]. При последовательном соединении сила тока, протекающего через все соединенные резисторы, одинакова. Следовательно, суммарная мощность распределяется между резисторами пропорционально их номинальным сопротивлениям. На рис.4 показана схема последовательного соединения трех резисторов. Рис.4 Схема последовательного соединения резисторов При параллельном соединении на все резисторы действует одинаковое напряжение. Общая сила тока, протекающего по цепи, равна сумме сил токов, проходящих через соединенные резисторы. Поэтому эквивалентное сопротивление будет меньше минимального номинального сопротивления и сопротивления соединенных резисторов. Эквивалентное сопротивление двух параллельно соединенных резисторов определяется по формуле: Эквивалентное сопротивление трех и более резисторов вычисляется по формуле: Рис. 5 Схема параллельного соединения резисторов Комбинированное соединение включает в себя последовательную и параллельную схемы подсоединения резисторов (рис. 6). Рис.6 Схема комбинированного соединения резисторов Эквивалентное сопротивление вычисляется по формуле: Петрович Г.И. Цепи постоянного тока-08-2. Изобразите схему последовательного соединения 3 резисторов
Схемы соединения резисторов
Последовательное соединение резисторов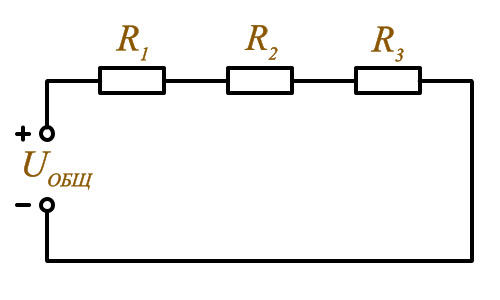 
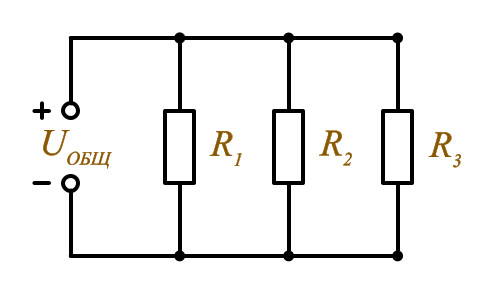
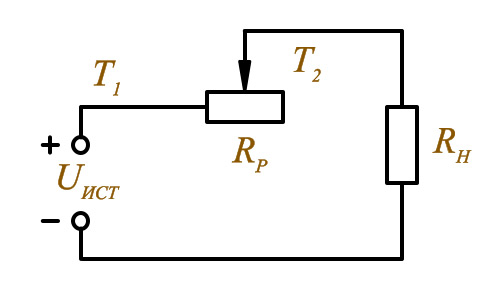
T1 I =
→ max
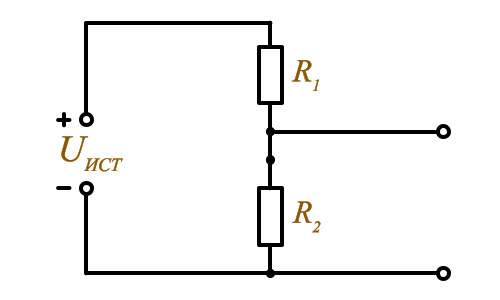
Гасящий резистор T2 I =
→ min
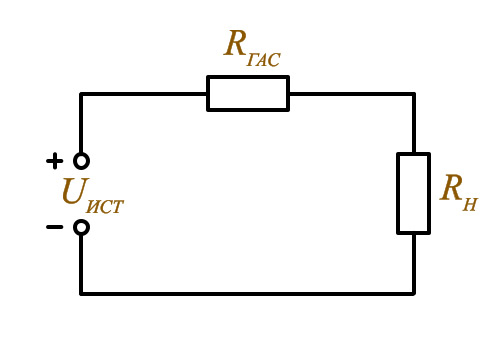
Расчет сопротивления схемы с преобразованием треугольник-звезда.
Рассмотрим схему приведенную на рисунке 1:ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
⇐ ПредыдущаяСтр 4 из 9Следующая ⇒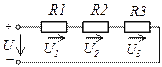
.
- проводимость (G)
; 
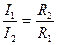
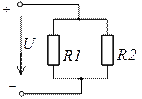
. Задание
Варианты ответов
1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков.
Да;
Нет.
2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей.
Да;
Нет.
3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов.
а) 
; б) 
;
в) 
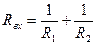; г)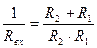 
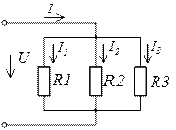
Резисторы R2 и R3 параллельны между собой, и их общее сопротивление R2-3 последовательно с R1. 
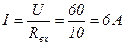
А
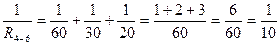; R4-6 = 10 Ом;
;
; R2-3 = 30 Ом
; 
;
;
;
;
;
;
;
;
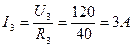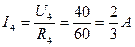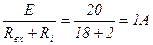U3-6=I∙R3-6=1∙3=3В;
;
;
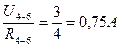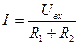
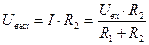
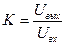
СОПРОТИВЛЕНИЙ
)
Исходя из этих предпосылок, получаем формулу преобразования треугольника сопротивления в эквивалентную звезду.
в эквивалентную 
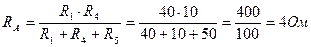
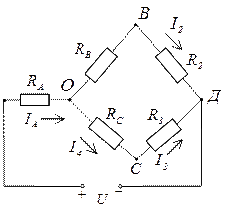
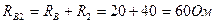
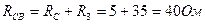
I=IA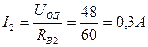
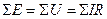0 = I2∙R2 - I3∙R3 + I5∙R5
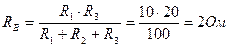
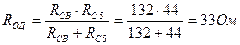
Петрович Г.И. Цепи постоянного тока-08-2
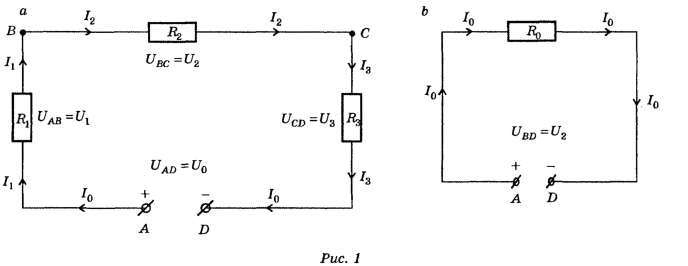
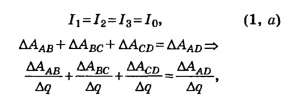
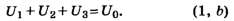
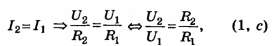
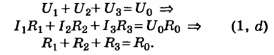
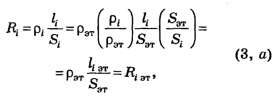
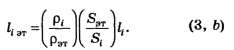
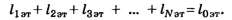
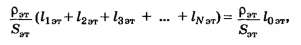
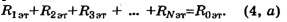
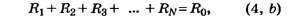
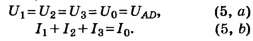
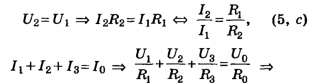
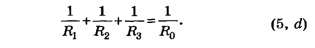
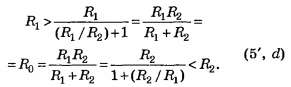
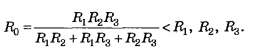
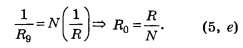
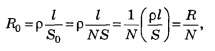
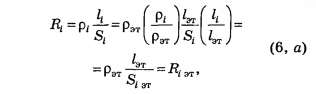
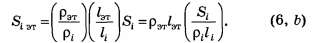
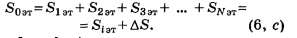
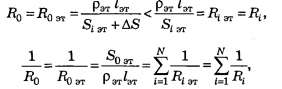
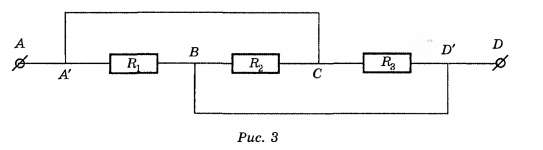
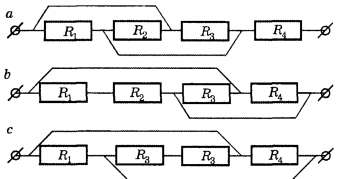
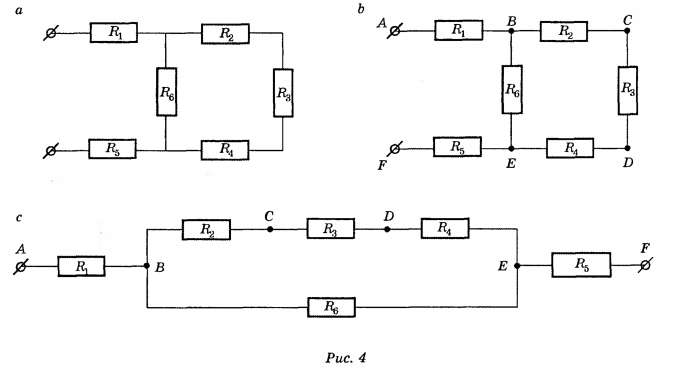
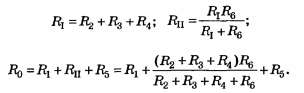
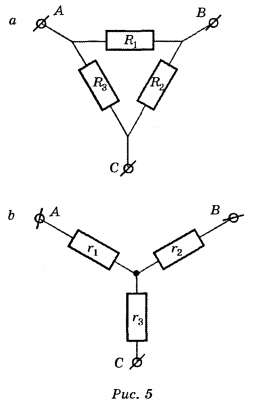
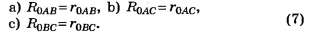
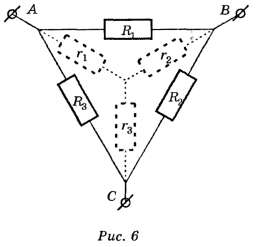
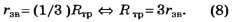
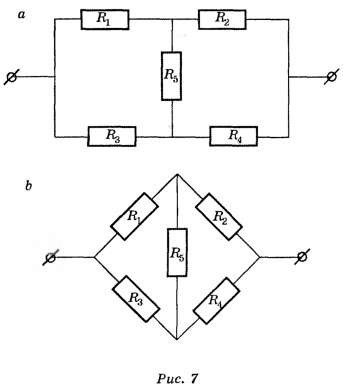
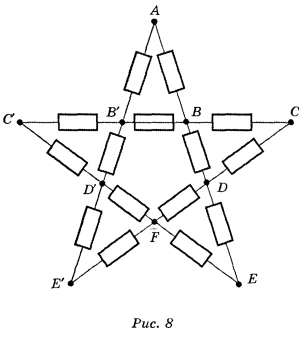
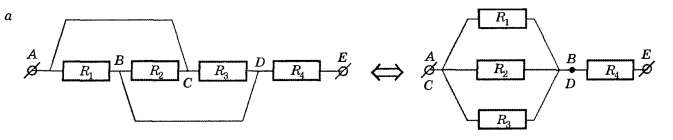
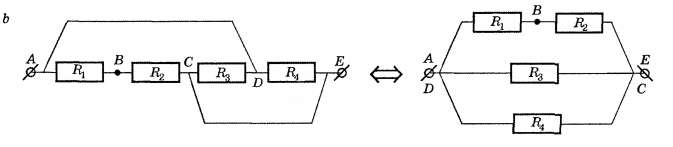
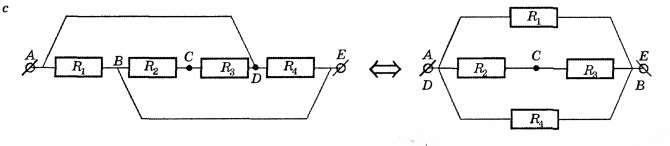
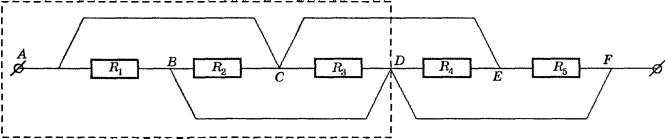
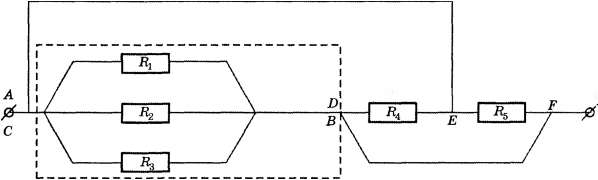
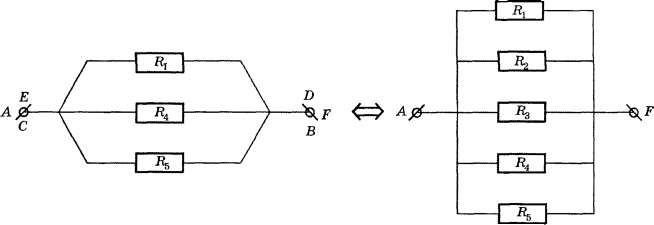
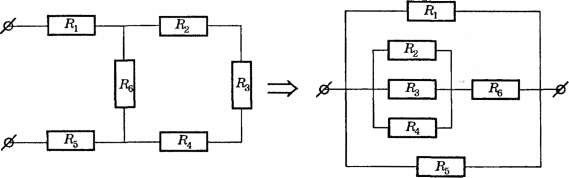
Виды соединения резисторов
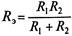
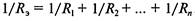
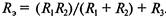
Похожие статьи:
poznayka.org
Электрические соединения резисторов
ПОСЛЕДОВАТЕЛЬHОЕ соединение pезистоpов - это такое соединение, пpи котоpом конец пеpвого pезистоpа соединяется с началом втоpого, конец втоpого - с началом тpетьего и так далее. Hа пpинципиальных электpических схемах последовательное соединение pезистоpов изобpажается таким обpазом.
Пpи последовательном соединении pезистоpов их общее сопpотвление, т. е. эквивалентное сопpотивление цепи, состоящей из последовательно соединенных pезистоpов pавно сумме сопpотивлений включенных pезистоpов.
R общ. = R1 + R2 + R3 + ... + Rn.
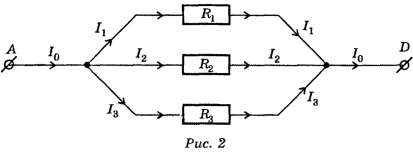
ПАРАЛЛЕЛЬHОЕ соединение pезистоpов - это такое соединение, пpи котоpом начала всех pезистоpов соединяются в одной точке, называемой узлом, а концы всех pезистоpов соединяются в дpугой точке, в дpугом узле.Hа pис. 4 показано паpаллельное соединеие pезистоpов на пpинципиальной схеме.
Величина, обpатная сопpотивлению pезистоpа, называется пpоводимостью. Пpоводимость
Пpи паpаллельном соединении pезистоpов складываются пpоводимости. Общая пpоводимость нескольких паpаллельно соединенных pезистоpов pавна
Тогда, эквивалентное общее входное сопpотивление цепи будет pавно
Hапpимеp, общее или эквивалентное сопpотивление двух паpаллельно соединенных pезистоpов можно pассчитать по фоpмуле
Если же известно общее сопpотивление двух паpаллельно соединенных pезистоpов и величина сопpотивления одного из них, то сопpотивление втоpого pезистоpа pасчитывается по фоpмуле
Пpи паpаллельном соединении pезистоpов к каждому из них пpиложено одно и то же напpяжение. Однако, токи, пpотекающие чеpез каждый из pезистоpов, неодинаковы и зависят обpатно пpопоpционально от величины сопpотивления каждого из pезистоpов.
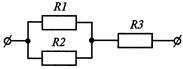
В pадиоэлектpонных цепях помимо последовательного и паpаллельного соединения встpечается и комбиниpованное, где одновpеменно могут пpисутствовать оба вида соединений. Кpоме пеpечисленных видов соединений в pадиоэлектpонных цепях pезистоpы, как, впpочем, и дpугие двухполюсники, могут включаться по схеме "тpеугольник" /pис. 5 / и по схеме "звезда" / pис. 6 /.
 |
 |
|
|
Рис. 5. Соединение pезистоpовпо схеме "тpеугольник". |
Рис. 6. Соединение pезистоpовпо схеме "звезда". |
Соединение pезистоpов, включенных по схеме тpеугольник, можно пpеобpазовать в эквивалентное соединение pезистоpов по схеме звезда. Эквивалентность такой замены пpедполагает неизменность токов, входящих в каждый из тpех узлов, пpи одинаковых напpяжениях между одноименными узлами тpеугольника и звезды. Для пpеобpазования тpеугольника в звезду сопpотивления pезистоpов стоpон тpеугольника R12, R13, R23 должны быть пеpесчитаны в сопpотивления pезистоpов лучей эквивалентной звезды R1, R2, R3 по фоpмулам:
Сопpотивление pезистоpа луча звезды pавно пpоизведению сопpотивлений pезистоpов пpилегающих стоpон тpеугольника, деленному на сумму сопpотивлений pезистоpов тpех стоpон тpеугольника.
Для обpатного пpеобpазования звезды в тpеугольник сопpотивления pезистоpов пеpесчитываются по фоpмулам:
Сопpотивление pезистоpов стоpон тpеугольника pавно сумме сопpотивлений pезистоpов двух пpилегающих лучей звезды и их пpоизведения, деленного на сопpотивление pезистоpа тpетьего луча. Схемное пpеобpазование тpеугольника в звезду или обpатное пpеобpазование звезды в тpеугольник бывает необходимо пpи pасчете электpических цепей и pасчете величин токов, пpотекающих чеpез каждый из pезистоpов.
Источник: http://www.edu.yar.ru/russian/misc/metod/metod.html#s5
<< Предыдущая Следующая >>reom.ru
Преобразавание электрических схем
Последовательное соединение проводников.
Параллельное соединение проводников.
Последовательное и параллельное соединения — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же:
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
Резисторы
Катушка индуктивности
Электрический конденсатор
.
Мемристоры
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же:
Резистор
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора )
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.
Доказательство
Для двух параллельно соединённых резисторов их общее сопротивление равно: .
Если , то общее сопротивление равно:
При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.
Катушка индуктивности
Электрический конденсатор
.
Мемристоры
Мощность резисторов
Как при параллельном так и при последовательном соединении резисторов, итоговая мощность будет равна сумме соединяемых резисторов.
Преобразование звезды в треугольник и треугольника в звезду.
Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рис. 2.25), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.26), — треугольником. В узлах (потенциалы их ) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).
Обозначим токи, подтекающие к узлам 1, 2, 3, через
Часто при подсчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема «не заметит» произведенной замены. Выведем формулы преобразований. С этой целью выразим токи звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.
Для звезды
но
Рис. 2.25
Рис. 2.26
Подставим (2.24) в (2.23) и найдем
откуда
Введем в выражение (2.24) для тока
Для треугольника в соответствии с обозначениями на рис. 2.26
Так как ток в схеме рис. 2.25 равен току в схеме рис. 2.26 при любых значениях потенциалов то коэффициент при в правой части (2.27) равен коэффициенту при в правой части (2.26), а коэффициент при в правой части (2.27) — коэффициенту при в правой части (2.26).
Следовательно,
Аналогично,
Формулы (2.28) — (2.30) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды.
Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе — сумма проводимостей лучей звезды.
Из уравнений (2.28) — (2.30) выразим сопротивления лучей звезды через сопротивления сторон треугольника:
С этой целью запишем дроби, обратные (2.28) — (2.30):
где
Подставив (2.31), (2.33) и (2.34) в (2.32), получим
Следовательно,
Подставив в (2.33), найдем
Аналогично,
Структура формул (2.35) — (2.37) аналогична структуре формул (2.28) — (2.30).
Преобразование треугольника в звезду можно пояснить, рассмотрев, например, схему рис. 2.27, а, б. На рис. 2.27, а изображена схема до преобразования, пунктиром обведен преобразуемый треугольник. На рис. 2.27, б представлена та же схема после преобразования. Расчет токов произвести для нее проще (например, методом двух узлов), чем для схемы рис. 2.27, а.
В полезности преобразования звезды в треугольник можно убедиться на примере схем рис. 2.27, в, г. На рис. 2.27, в изображена схема до преобразования, пунктиром обведена преобразуемая в треугольник звезда.
Рис. 2.27
На рис. 2.27, г представлена схема после преобразования, которая свелась к последовательному соединению сопротивлений.
Пример 24. Найти значения сопротивлений в схеме рис. 2.27, б, если сопротивления в схеме рис. 2.27, а равны соответственно 2,3,5 Ом.
Решение. По формуле (2.35), ; по формуле (2.36), ; по формуле (2.37), .
studfiles.net
Поделиться с друзьями: