В задачах с присутствием конденсаторов очень часто нужно уметь находить емкость последовательного и параллельного соединения емкостей. С параллельным соединением емкостей все просто: при параллельном соединении емкости складываются. Почему это так? Дело в том, что при параллельном соединении на всех конденсаторах одинаковое напряжение, а их заряды пропорциональны емкостям: Общий заряд на конденсаторах: Тогда емкость системы конденсаторов: С последовательным соединением все сложнее. Кстати, когда готовила эту статью, наткнулась на такой вот перл, который не могла не процитировать: Заряды при последовательном соединении одинаковы на всех конденсаторах: Тогда напряжение между крайними точками равно: Емкость всей системы: 1. Разность потенциалов между точками А и В Задача 1 Определим общую емкость такого соединения: Тогда заряд равен: Заряды при последовательном соединении на всех конденсаторах одинаковые, значит для первого: Напряжения на конденсаторах: Ответ: 18 мкКл, 6 В, 3 В.2. Определите емкость батареи конденсаторов, изображенной на рисунке. Емкость каждого конденсатора Задача 2 Емкости Ответ: 286 нФ 3. Емкость батареи конденсаторов, образованной двумя последовательно включенными конденсаторами, 100 пФ, а заряд 20 нКл. Определите емкость второго конденсатора, а также разность потенциалов на обкладках каждого из них, если Воспользуемся Отсюда При последовательном соединении заряд на конденсаторах равный: Напряжения также получатся одинаковыми: Ответ: 4. Наибольшая емкость конденсатора 60 мкФ. Какой заряд он накопит при подключении источника постоянного напряжения 60В? Так как Ответ: 0,36 мКл 5. При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 100 В. Какова диэлектрическая проницаемость диэлектрика? Рассмотрим сначала конденсатор до введения диэлектрика: Тогда Емкость конденсатора, как известно, зависит от площади пластин и расстояния между ними, а также от диэлектрика: В первом случае, без диэлектрика: Найдем и в этом случае отношение емкостей: Ответ: 6. Площадь пластин конденсатора равна 520 см кв. На каком расстоянии нужно разместить пластины в воздухе, чтобы емкость конденсатора была равна 50 пФ? Емкость конденсатора без диэлектрика: Площадь нужно выразить в кв. метрах: Диэлектрическая проницаемость воздуха Выразим из первого выражения нужную нам величину: Ответ: 9,2 мм 7. Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора? Энергию электрического поля, накопленную конденсатором, можно вычислить по формуле: Тогда: 8. Расстояние между пластинами плоского конденсатора с диэлектриком из бумаги, пропитанной парафином, равно 2 мм, а напряжение 200 В. Найти плотность энергии поля. Чтобы найти плотность энергии, нужно сначала определить энергию поля, а потом посчитать, в каком объеме она сосредоточена. Посмотрим в справочнике, какова диэлектрическая проницаемость бумаги с парафином, выразим расстояние между пластинами в метрах, и подставим цифры: easy-physic.ru Для подбора нужной электроемкости, соответствующей данному рабочему напряжению, приходится часто соединять конденсаторы в батарею. При этом возможно параллельное, последовательное и смешанное соединение конденсаторов. Рассмотрим каждый из видов соединения конденсаторов в отдельности. 1.5.1. Параллельное соединение конденсаторов Параллельное соединение конденсаторов применяется в основном для увеличения емкости. Определим емкость батареи конденсаторов, соединенных между собой параллельно (рис. 1.3) Рис.1.3. Параллельное соединение конденсаторов Пусть емкости каждого из конденсаторов соответственно равны С1, С2, С3. При параллельном их соединении разность потенциалов между обкладками конденсаторов будет одинакова, а заряд на обкладках распределиться прямо пропорционально емкости: Сложив почленно эти равенства, получим: Сумма зарядов на обкладках конденсаторов определяет заряд батарее для батареи конденсаторов, соединенных параллельно имеем q = СU, где Таким образом, при параллельном соединении конденсаторов емкость батареи равна сумме емкостей конденсаторов, входящих в батарею. 1.5.2. Последовательное соединение конденсаторов. Последовательное соединение конденсаторов - это соединение, при котором отрицательная обкладка одного конденсатора соединяется с положительной обкладкой другого конденсатора (рис.1.4) Рис.1.4. Последовательное соединение конденсаторов Если первой обкладке конденсаторов сообщить заряд +q, то на второй его обкладке вследствие индукции возникнет заряд -q, а на соединенной с ней первой обкладке второго конденсатора появится заряд +q и т.д. Следовательно, заряд на всех обкладках будет иметь одинаковое значение q, а разность потенциалов U распределиться между конденсаторами обратно пропорционально их емкости: Разность потенциалов между крайними обкладками равна сумме разностей потенциалов между обкладками всех последовательно соединенных конденсаторов: И Следовательно, при последовательном соединении конденсаторов величина, обратная емкости батареи конденсаторов, равна сумме величин, обратных емкостям отдельных конденсаторов. При последовательном соединении конденсаторов электроемкость батареи меньше электроемкости каждого из конденсаторов. 1.5.3. Смешанное соединение конденсаторов Смешанное соединение конденсаторов представляет собой различные комбинации параллельного и последовательного соединений (рис. 1.5). Рис:1.5. Смешанное соединение конденсаторов Для расчета емкости батареи при смешанном соединении пользуются формулами (1.12) и (1.13). При заряжении проводника совершается работа против электрических сил отталкивания между одноименными зарядами, сообщаемыми проводнику. Работа эта идет на увеличение электрической энергии заряженного проводника. Для подсчета электрической энергии заряженного проводника допустим, что вначале проводник был не заряжен. Сообщим ему количество электричества q. Тогда вокруг проводника возникнет электрическое поле, и потенциал проводника примет значение где С - емкость данного уединенного проводника. Для того, чтобы увеличить заряд проводника на dq необходимо перенести этот заряд из бесконечности на поверхность проводника, совершив при этом работу dA , равную Потенциальная энергия проводника в этом случае увеличится на dW Полная работа по переносу всех зарядов из бесконечности на поверхность проводника при заряжении последнего от потенциала 0 до потенциала определится суммой всех работ dA, т. е. интегралом, взятым в пределах от 0 до : Так как Эта работа численно равна энергии заряженного проводника W Электрическая энергия проводника равна половине произведения его заряда на потенциал. studfiles.net Cтраница 1 Емкость батареи конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов. [2] Емкость батареи конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов. Так как в этом случае напряжение на каждом конденсаторе равно напряжению на батарее, то и допустимое рабочее напряжение батареи будет таким же, как и у одного конденсатора. [4] Какая емкость батареи конденсаторов требуется для получения реактивной ( емкостной) мощности 152 вар, при напряжении U127 в и чхс-тоте / 50 гц. [5] Определить емкость батареи конденсаторов, подключенной параллельно к этому электродвигателю для повышения коэффициента мощности установки до 0 95, и ток в подводящих проводах поел подключения конденсаторов. [6] Установив емкость батареи конденсаторов 15 - 20 мкФ, замкните полностью магнитопровод катушки трансформатора. [7] Найти емкость получившейся батареи конденсаторов, если эта батарея включается в цепь проводниками, присоединенными к противоположным вершинам ( Л и В) куба. [8] Следовательно, емкость батареи конденсаторов при данной реактивной мощности обратно пропорциональна квадрату напряжения. Поэтому для увеличения коэффициента мощности установки в цепи высокого напряжения требуется меньшая емкость, чем в цепи низкого напряжения. [9] Однако увеличение емкости батареи конденсаторов в рабочем режиме нежелательно, так это ведет к снижению частоты вращения и кпд двигателя. Поэтому конденсаторные двигатели выполняют с двумя батареями конденсаторов - рабочей и пусковой. [10] Для определения емкости батареи конденсаторов используются закон сохранения заряда и формула электроемкости конденсатора. [11] Реактивная мощность и емкость батареи конденсаторов QC Q1 - Q3 56 - 30 5 25 5 квар. [12] Рассмотрим пример расчета емкости батареи конденсаторов, которую необходимо включить параллельно индуктивному потребителю с со5фп, чтобы довести коэффициент мощности установки до заданного значения созф. Активная мощность и напряжение потребителя заданы. [13] Рассмотрим пример подсчета емкости батареи конденсаторов, которую необходимо подключить параллельно индуктивному потребителю с со5фп, чтобы довести коэффициент мощности установки до заданного значения costp. Активная мощность и напряжение потребителя заданы. [15] Страницы: 1 2 3 4 www.ngpedia.ru Система из нескольких конденсаторов называется батареей. Рассмотрим два типа соединения конденсаторов в батарею. Параллельное соединение (рис. 90). У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна (φА – φВ ). Если емкости конденсаторов С1 , С2 , …Сn , то Q1 = C1 (φА – φВ ) Q2 = C2 (φА – φВ ) Q3 = C3 (φА – φВ ) . . . . . . . . . . . . . Qn = Cn (φА – φВ ). Заряд батареи будет равен сумме зарядов Q = = (C1+C2+. . .+Cn)(φА–φВ). Полная емкость батареи будет равна С = = (C1 + C2 + . . . + Cn ) = . Последовательное соединение (рис. 91) У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи Δφ равна Δφ = , где разность потенциалов для любого из рассматриваемых конденсаторов равна. Таким образом, разность потенциалов батареи конденсаторов будет По определению , откуда получаем При последовательном соединении суммируются обратные величины емкостей и результирующая емкость батареи С всегда меньше наименьшей емкости, используемой в батарее. Энергия системы точечных неподвижных зарядов. Электростатические силы консервативны и система зарядов обладает потенциальной энергией. Пусть заряды Q1 и Q2 находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией , где φ12 и φ21 – соответственно потенциалы, создаваемые зарядом Q2 в точке нахождения заряда Q1 , и наоборот. ; . Поэтому W1 = W2 =W = Q1 φ12 = Q2 φ21 = ½ (Q1 φ12 + Q2 φ21). Добавляя к системе из двух зарядов последовательно заряды Q3 , Q4 , …, Qn, можно убедиться, что энергия взаимодействия системы зарядов равна , где φi – потенциал, создаваемый в той точке, где находится заряд Qi , всеми зарядами, кроме i-го. Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого Q, C, φ. Увеличим заряд на dQ. Для этого необходимо перенести заряд dQ из бесконечности к поверхности проводника, затратив на это работу, равную dA = φdQ = C φd φ Чтобы зарядить тело от нулевого потенциала до потенциала равного φ необходимо совершить работу Энергия заряженного проводника будет равна этой работе Учитывая, что , эту энергию можно представить в виде Энергия заряженного конденсатора. Как всякий заряженный проводник, конденсатор обладает энергией где Q - заряд конденсатора, С – его емкость и Δφ – разность потенциалов между обкладками. Используя выражение для энергии, можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется на величину dx. Тогда действующая сила совершает работу равную dA =Fdx за счет уменьшения потенциальной энергии Fdx = - dW, откуда . Подставляя в формулу энергии выражение емкости, получим . Дифференцируя W по х, найдем силу F , где знак “минус“ указывает, что сила F стремится уменьшить расстояние между пластинами, т.е. является силой притяжения. Подставляя выражение плотности зарядов на пластинках , получим. Учитывая напряжённость поля, что Е = , получим . Давление на пластины диэлектрика, помещенные в зазоре конденсатора, будет Энергия электростатического поля. Преобразуем формулу энергии плоского конденсатора, используя формулыи Δφ = Еd. Получим , где V – объем пространства между пластинами конденсатора, в котором сосредоточена энергия его поля W. Объемная плотность энергии поля w – это энергия, заключённая в единице объёма электрического поля и она равна . Единица измерения [Дж/м3]. Видно, что объемная плотность энергии поля зависит только от характеристик поля и среды. studfiles.net «Электроёмкость» - последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22). Задача 1. Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C 1 = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Р е ш е н и е. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq - (С 2 - C)U = (nC 1 - C 1)U = (п - 1)С 1 U = 10 -8 Кл. Задача 2. Заряд конденсатора q = 3 10 -8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона Р е ш е н и е. Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А - работа электрического поля конденсатора: Следовательно, Окончательно Задача 3. Четыре конденсатора ёмкостями С 1 = С 2 = = 1 мкФ, С 3 = 3 мкФ, С 4 = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов. Р е ш е н и е. Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С 2,3 = С 2 + С 3 , а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С 1 , С 2,3 , С 4 , найдём из соотношения 1/Cэкв = 1 /С 1 + 1/С 2,3 + 1 /С 4 , Сэкв = (4/7) 10 -6 Ф. Заряды на этих конденсаторах одинаковы: q 1 = q 2,3 = q 4 = Сэкв = 8 10 -5 Кл. Следовательно, заряд первого конденсатора q 1 = 8 10 -5 Кл, а разность потенциалов между его обкладками, или напряжение, U 1 = q 1 /С 1 = 80 В. Для четвёртого конденсатора аналогично имеем q 4 = 8 10 -5 Кл, U 4 = q 4 /C 4 = 40 В. Найдём напряжение на втором и третьем конденсаторах: U 2 = U 3 = q 2,3 /C 2,3 = 20 В. Таким образом, на втором конденсаторе заряд q 2 = C 2 U 2 = 2 10-5 Кл, а на третьем конденсаторе q 3 = C 3 U 3 = 6 10 -5 Кл. Отметим, что q 2,3 = q 2 + g 3 . Задача 4. Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны. Р е ш е н и е. Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов. В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φ A ≠ φ B в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и С экв определим по формуле 1/С экв = 1/2С 1 + 1/2С 2 , откуда Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно, Эквивалентные конденсаторы с С" экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости: Задача 5. Энергия плоского воздушного конденсатора W 1 = 2 10 -7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если: 1) конденсатор отключён от источника питания; 2) конденсатор подключён к источнику питания. Р е ш е н и е. 1) Так как конденсатор отключён от источника питания, то его заряд ruscos.ru Конденсаторы соединены в батарею по схеме изображенной на рисунке. Определить какой заряд необходимо сообщить батарее, чтобы зарядить ее до напряжения 500 Вольт. Емкость конденсаторов: С1=4×10-6 Ф; С2=6×10-6 Ф; С3=8×10-6 Ф; С4=12×10-6 Ф. Дано: С1=4×10-6 Ф; С2=6×10-6 Ф; С3=8×10-6 Ф; С4=12×10-6 Ф; U=500 ВНайти: q — ? Решение: Емкость батареи конденсаторов определим из соотношения Заряд батареи конденсаторов определим по формуле Ответ: батареи конденсаторов необходимо сообщить заряд 1,235×10-3 Кулон Поделитесь с друзьями: zadachi-po-fizike.electrichelp.ruСоединение конденсаторов в батарею. Чему равна емкость батареи конденсаторов соединенных по схеме
Конденсаторы - задачи
 и т.д.
и т.д.
 .
.
 и т.д.
и т.д.
 , или
, или 
 В. Емкость конденсаторов соответственно равна
В. Емкость конденсаторов соответственно равна  мкФ и
мкФ и  мкФ. Определите заряды
мкФ. Определите заряды  и
и  и разности потенциалов
и разности потенциалов  и
и  на обкладках первого и второго конденсаторов.
на обкладках первого и второго конденсаторов.
 ,
, мкФ (сразу считаем в микрофарадах, чтобы не расписывать степени десятки)
мкФ (сразу считаем в микрофарадах, чтобы не расписывать степени десятки) мкКл.
мкКл. , для второго
, для второго  .
. В,
В,  В.
В. мкФ.
мкФ.
 и
и  , поскольку они соединены параллельно, необходимо сложить:
, поскольку они соединены параллельно, необходимо сложить:  мкФ. Тогда получим последовательное соединение трех одинаковых емкостей и
мкФ. Тогда получим последовательное соединение трех одинаковых емкостей и  , емкость которой вдвое больше. При последовательном соединении емкостей их эквивалентная емкость вычисляется по формуле:
, емкость которой вдвое больше. При последовательном соединении емкостей их эквивалентная емкость вычисляется по формуле:  . Тогда получим:
. Тогда получим:  ,
,  мкФ.
мкФ. пФ.
пФ. . Тогда
. Тогда  (считаем в пикофарадах)
(считаем в пикофарадах) ,
,  ,
,  пФ.
пФ. нКл.
нКл. В,
В,  В.
В. В,
В,  нКл.
нКл. , то
, то  мКл.
мКл. ,
,  . Заряд остался тем же при введении диэлектрика, а напряжение изменилось:
. Заряд остался тем же при введении диэлектрика, а напряжение изменилось:  .
. , или
, или 

 , а во втором
, а во втором 
 , или
, или 
 Кл*Кл/Н*м*м
Кл*Кл/Н*м*м

 .
. м, или 9,2 мм.
м, или 9,2 мм. – и в этой задаче как раз хорошо будет воспользоваться второй записью.
– и в этой задаче как раз хорошо будет воспользоваться второй записью. мкДж
мкДж , с другой стороны, емкость
, с другой стороны, емкость  , тогда
, тогда  . Объем пространства между пластинами конденсатора – это произведение площади пластин на расстояние между ними:
. Объем пространства между пластинами конденсатора – это произведение площади пластин на расстояние между ними:  . Тогда плотность энергии поля равна
. Тогда плотность энергии поля равна 
 мДж
мДж1.5. Соединение конденсаторов
1.6. Энергия уединенного заряженного проводника
Емкость - батарея - конденсатор
Емкость - батарея - конденсатор
Соединение конденсаторов в батарею
Энергия зарядов, проводников, конденсаторов и электростатического поля. Объемная плотность энергии
Найти общую емкость батареи конденсаторов. Последовательное соединение конденсаторов
Пример решения задачи на определение заряда батареи конденсаторов
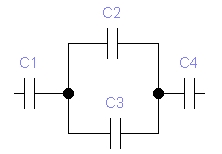
 , откуда
, откуда
 , тогда
, тогда

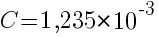 Кл
Кл
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: